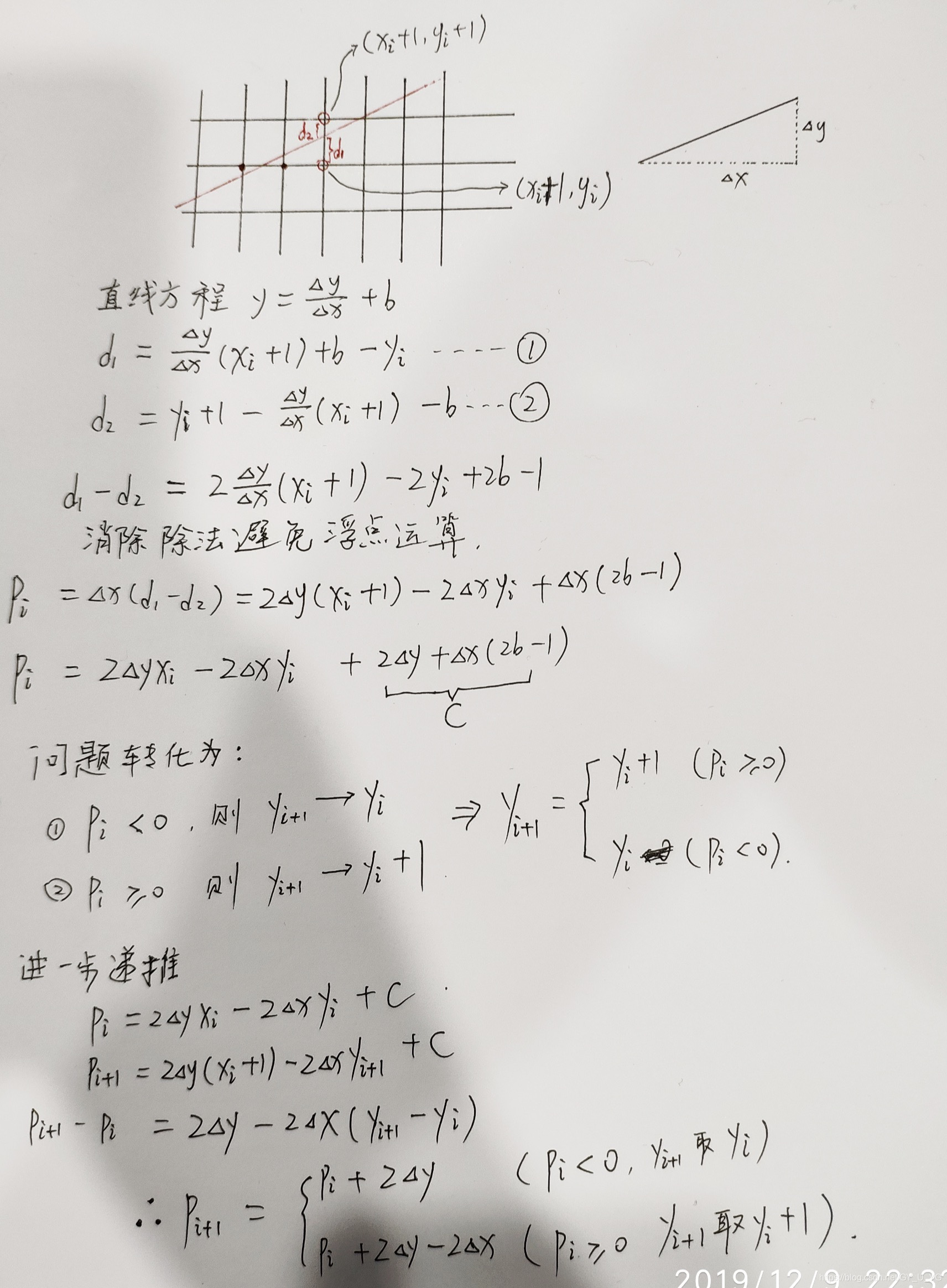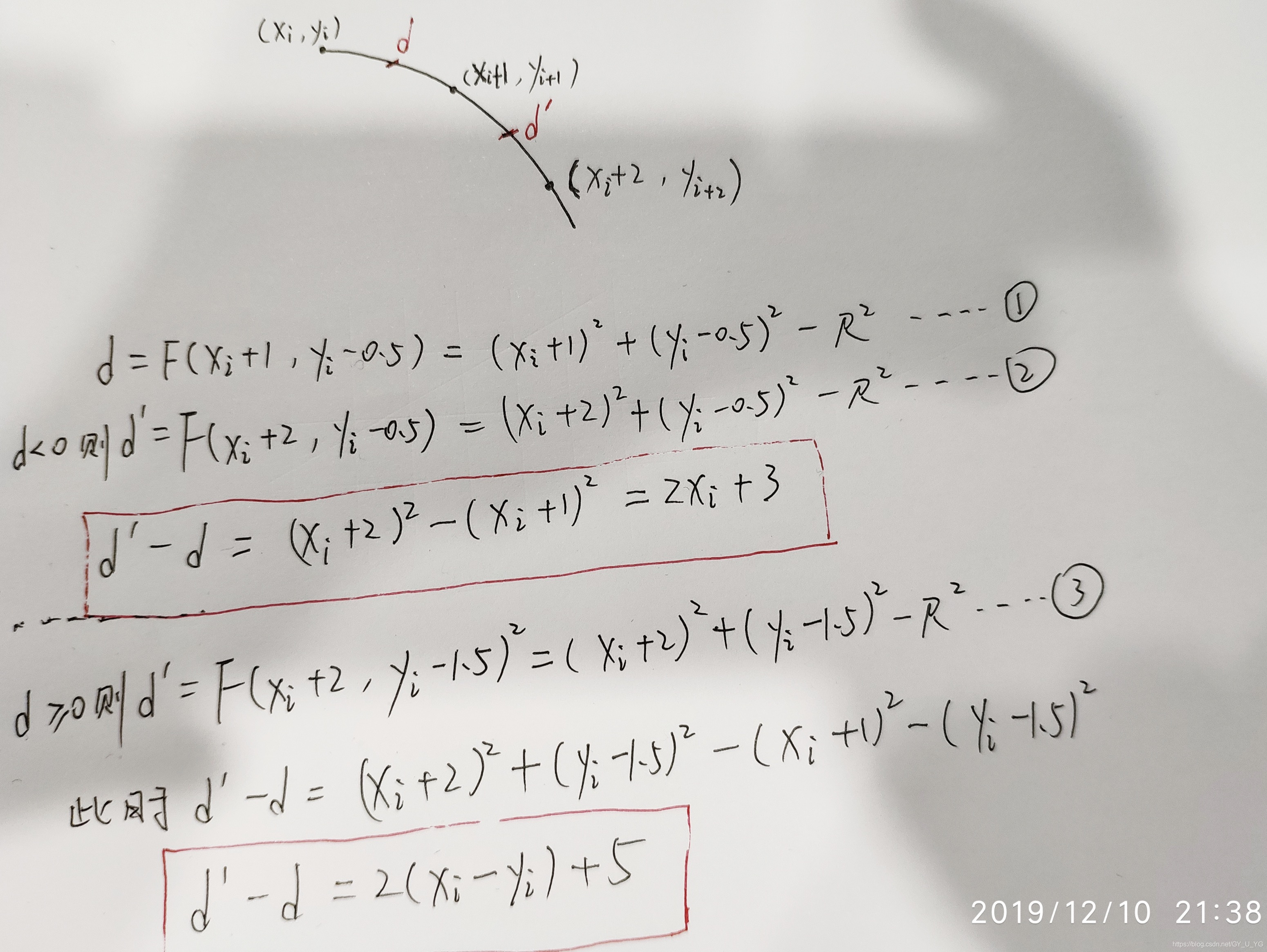一、什么是图元
图元是基本的几何图形,图元是构成其他复杂图形的基本要素,比如:点、线段、、三角形、矩形、圆弧、圆角矩形、扇形等等。
这些图元可以构成其他的复杂图形,在底层被大量的调用执行。
注:比如业务层一个动画、一个复杂的图形,对于画直线函数的调用可能是成百上千次,甚至是成千上万次的,所以图元算法的优劣对性能的影响是非常大的。
二、什么是OpenGL
OpenGL的英文名称:Open Graphics Library 。开放式图形库、三维图形处理库,开放性图形库 等等,用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口(API)的规范。
这个首先说明一点,OpenGL并不是一个API库,而是一个标准,一个规范。这个规范严格的规定了每个函数要如何执行、以及函数的输出值,至于每个函数具体的实现过程、是由各个厂商的开发者,也就是OpenGL库的开发者根据自己的硬件特性开发出相应的API。市场上,OpenGL大都是显卡厂商、GPU厂商、以及浏览器厂商比如Mozilla、Google等尖端科技公司来实现。
OpenGL对性能的要求非常高,所以,OpenGL注定要用C语言之类实现。
OpenGL的实现,是对数学思想淋漓尽致的发挥,是人类智慧的精华,这里可以体会到数学的魅力,OpenGL的背后是深奥美妙的计算机图形学,说白了就是数学。
OpenGL ES(OpenGL for Embedded Systems,OpenGL嵌入式版本,针对手机、游戏机等设备相对较轻量级的版本)
三、OpenGL用途
OpenGL标准已经广泛应用到IT各个领域,比如游戏开发,我们熟知的Unity-2d、Unity-3d、cocos-2d等游戏引擎底层实现都依赖于OpenGL。
- GLFW——跨平台窗口和键盘、鼠标、手柄处理;偏向游戏
- freeglut——跨平台窗口和键盘、鼠标处理;API 是 GLUT API 的超集,同时也比 GLUT 更新、更稳定
- GLUT——早期的窗口处理库,已不再维护
- Allegro 5——跨平台多媒体库,提供针对游戏开发的 C API
- SDL——跨平台多媒体库,提供 C API
- Qt——跨平台 C++ 窗口组件库,提供了许多 OpenGL 辅助对象,抽象掉了桌面版 OpenGL 与 OpenGL ES 之间的区别
- wxWidgets——跨平台 C++ 窗口组件库
- Skia——谷歌公司的图形渲染引擎用于Android操作系统、Chrome浏览器图形绘制。
四、关于DirectX
说到OpenGL就不得不提到DirectX,两者是竞争对手关系。
DirectX并不是一个单纯的图形API,它是由微软公司开发的用途广泛的API,DirectX是由很多API组成的,按照性质分类,可以分为四大部分,显示部分、声音部分、输入部分和网络部分。
我们可接触到的图形API可分为OpenGL和DirectX两大体系,前者是一项开放性的标准,主攻专业图形应用和3D游戏,由"OpenGL架构委员会"掌控,其成员包括业内各大厂商。
如果你想进行PC,Windows 相关的开发(不仅仅局限于游戏开发),选择DirectX。
如果你想进行Android、iOS、MacOS 、Linux等平台的游戏开发或相关专业图形开发,或者喜欢跨平台的特性,选择OpenGL。
五、什么是webGL
webGL是什么?就是一层皮,是OpenGL的一层皮!
webGL:(全写 Web Graphics Library )是一种 3D 绘图标准,这种绘图技术标准允许把 JavaScript 和 OpenGL ES 2.0 结合在一起,通过增加 OpenGL ES 2.0 的一个 JavaScript 绑定,或者笼统的理解为webGL就是在OpenGL上有包了一层皮,让你可以不需要使用C/C++,而是使用JavaScript也能做3D图形开发。
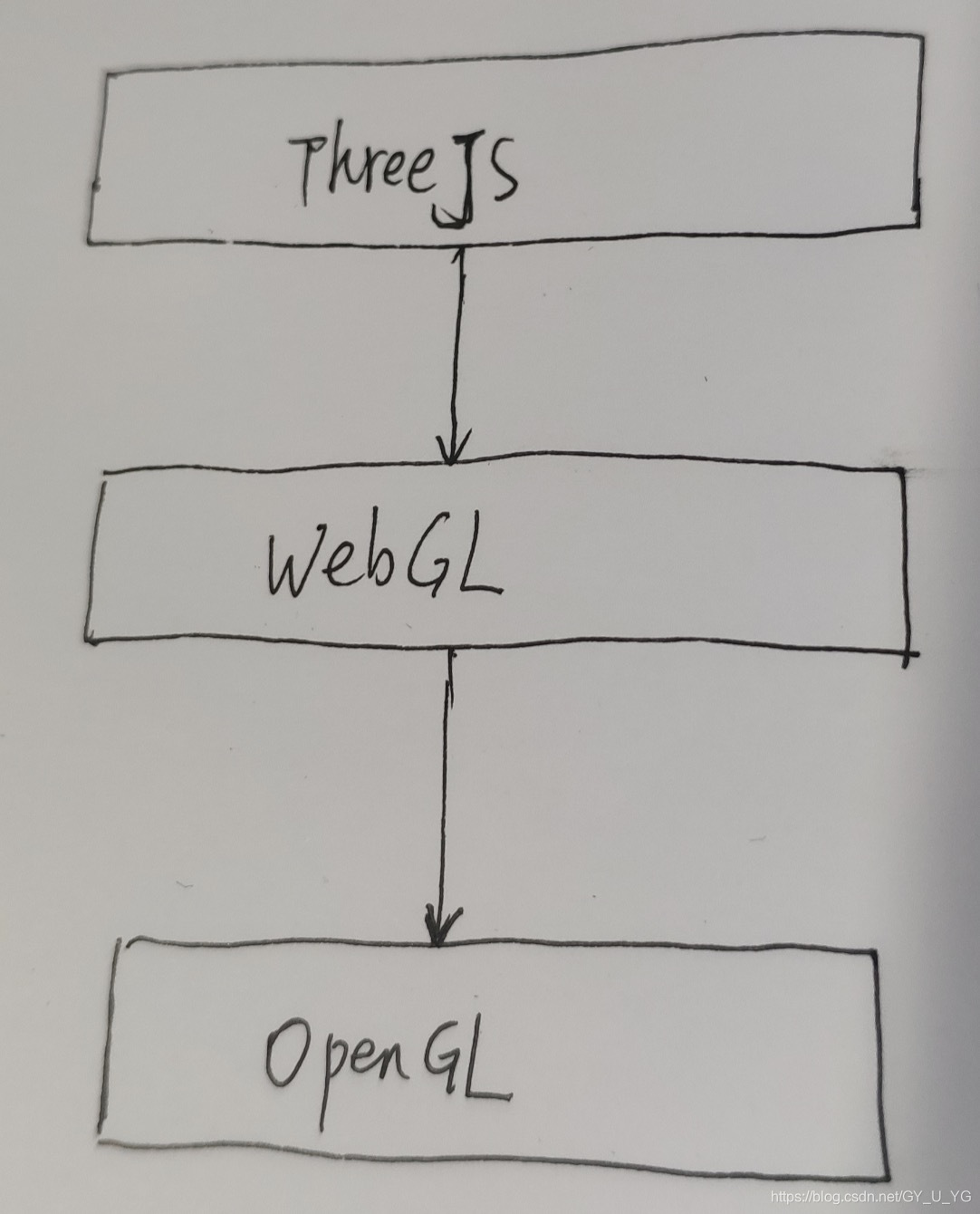
六、什么是ThreeJS
ThreeJS是什么?就是一层皮,是webGL的一层皮!
但是使用JavaScript就能直接做3D图形,其实也没那么简单,直接操作webGL,使用起来还是很晦涩的,因为需要调参,调参需要深厚的数学功底和图形学理论,所以,一般人搞不了这事儿!
这个时候,有个西班牙的程序员对webGL做了更进一步的JS封装,让前端程序员使用起来更快捷、方便!
这里加个图(threejs.jpeg)
七、关于Babylon.js
BabylonJS是最好的开发游戏的JavaScript库,更倾向于创建专业的3d游戏,是微软开发的。说一嘴,BabylonJS也是基于webGL标准的库,这个和webGL是一样的底层。
BabylonJS对webGL的封装很深,更容易使用,不易扩展;
ThreeJS对webGL的封装较浅,易于向底层学习,但是用起来没有babylonJS方便;
ThreeJS文档较少,不利于学习,BabyLonJS文档丰富,由微软做支撑。
八、硬件加速和GPU
硬件加速:在计算机中通过把计算量非常大的工作分配给专门的硬件来处理以减轻中央处理器的工总量的技术,尤其是在图形处理中,硬件加速用的非常普遍!在图形处理中,有专门用于计算图形的芯片,叫GPU,GPU已经是显卡的核心部件。
GPU:Graphics Processing Unit,翻译为图形处理单元,意译为显示核心、显示芯片,GPU使得显卡减少了对CPU的依赖,解放出CPU用于CPU原本的工作。
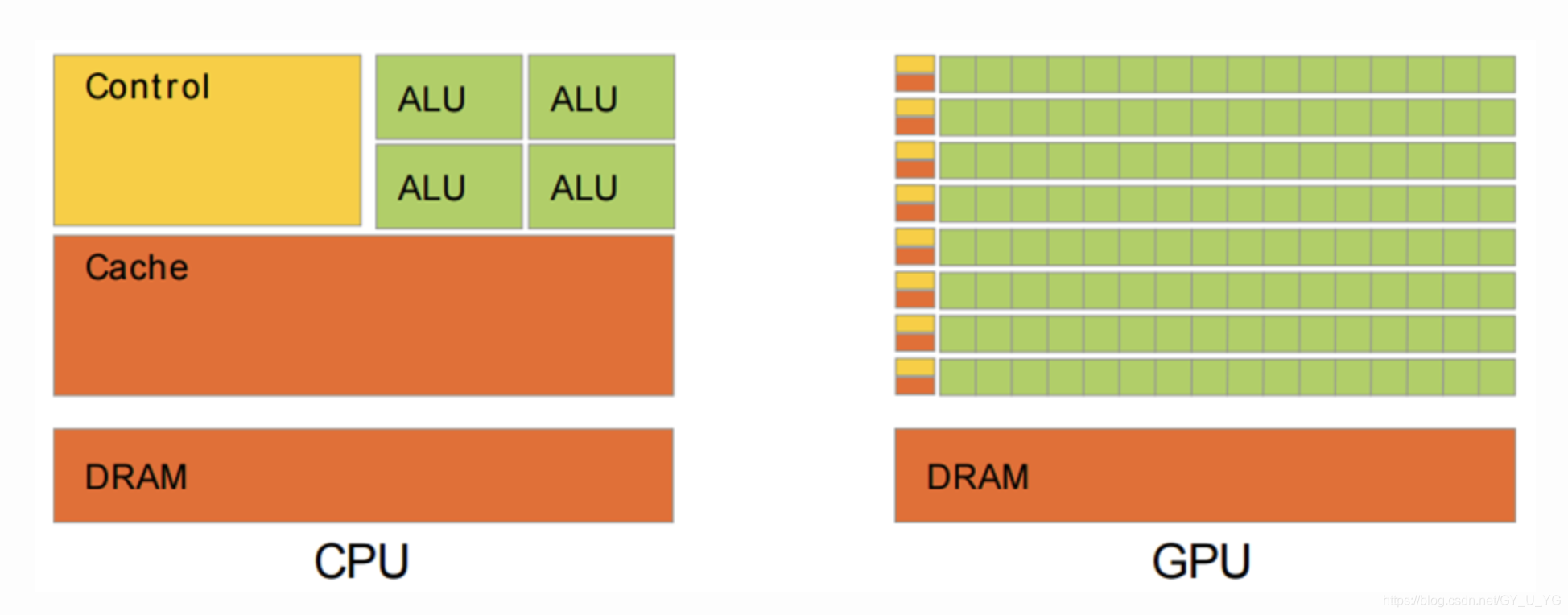
这里加个图(gpu.png桌面上)
图中黄色部分是控制器(Control),用于协调整个CPU的管理、调度,是一个管理者的角色;
图中绿色部分是ALU(Arithmetic Logic Unit),算术逻辑单元,顾名思义,主要是做数学运算以及逻辑运算的;
从图中的结构可以看出,CPU的控制器较为复杂,而ALU数量较少。因此CPU擅长各种复杂的逻辑运算,但不擅长数学尤其是浮点运算,因为CPU讲究的综合能力,不仅仅只是运算能力,运算能力只是CPU的一部分。
但是GPU就不一样了,GPU就是专门为运算而生的,主职工作就是做数学计算。
- CPU是串行结构,对于其中的一个单核来说,每次只能计算两个数的和,将结果逐步累加,有少量的浮点运算器,或者没有。构造简单的CPU甚至只有加法器,通过加法器和补码做减法,有了加减法,就可以做乘除法。
- GPU是并行结构,图中可以看到GPU包含了大量的ALU,就是为了实现大量的数学运算而设计的,并且GPU中有很多浮点运算器。
为什么要强调浮点运算,因为浮点运算效率很低,需要消耗更多的时间,以Intel的8086微处理器来说,一次整形的加法需要 1 - 3个机器周期,而浮点运算一次运算需要上百个机器周期,所以,我们写代码,要尽量少的出现浮点运算,我们可以通过数学方式将浮点运算转化成整形运算,至于怎么转化,在计算机图形学里面有大量的案例!
有了上面的知识做铺垫:我们可以很直观的理解,硬件加速的主要原理就是通过底层软件代码,将CPU不擅长的图形计算转换成GPU专用的指令,由GPU完成!
九、光栅化
什么是光栅化?
光栅化是将几何数据经过一系列变换后最终转换成像素,从而呈现在显示设备上的过程
有了以上的基本认知,我们首先来看看如何在屏幕上画直线(线段)
由于屏幕是由一个一个像素点排列而成的,而且像素点和像素点之间还是有间距的,所以在屏幕上画直线,不是按照严格意义的数学公式直线来的,因为按照数学公式的直线经过的地方可能并没有可发光的像素点。所以,在屏幕上画线,我们只是选择非常趋近于这条数学直线的像素点来“拼凑”出一条直线。
数学上的直线没有宽度,是由无限个点构成的集合,是一种理论上的理想情况,光栅显示器只能近视的显示直线,当我们对直线进行光栅化处理时,需要在显示器的有限个像素点中,选择最佳逼近该理想直线的一组像素,扫描式的写入像素,这个过程叫做用显示器绘制直线,或者叫做 直线的扫描转换。
因此,屏幕上的直线可以理解为有限个点阵的集合,后面我们就进行。
计算机图形学中常见的画线法有三种:DDA算法、中点画线法、Bresenham算法,这些算法不仅仅可以画直线,还可以画曲线,也是OpenGL等计算机图形学的API中图元绘制的核心思想,非常重要!
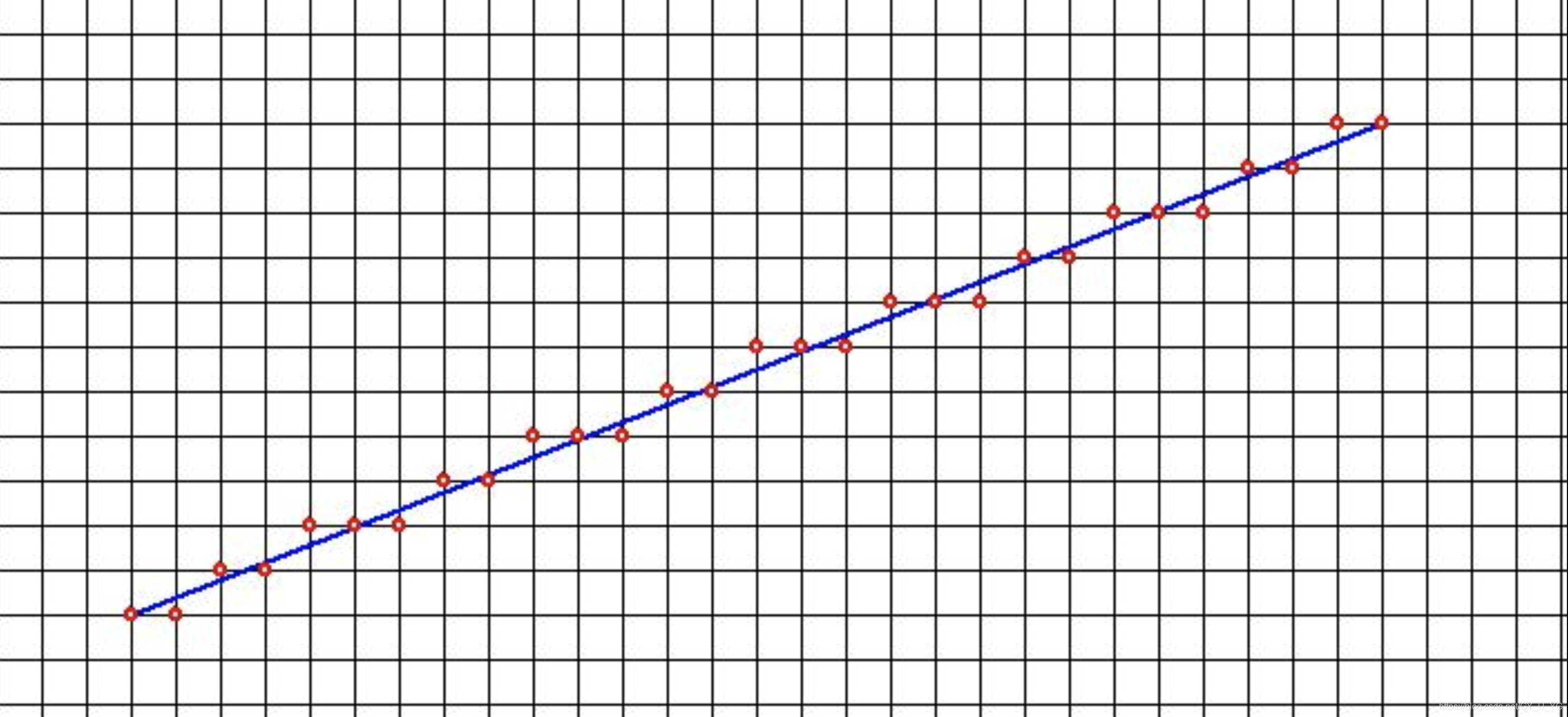
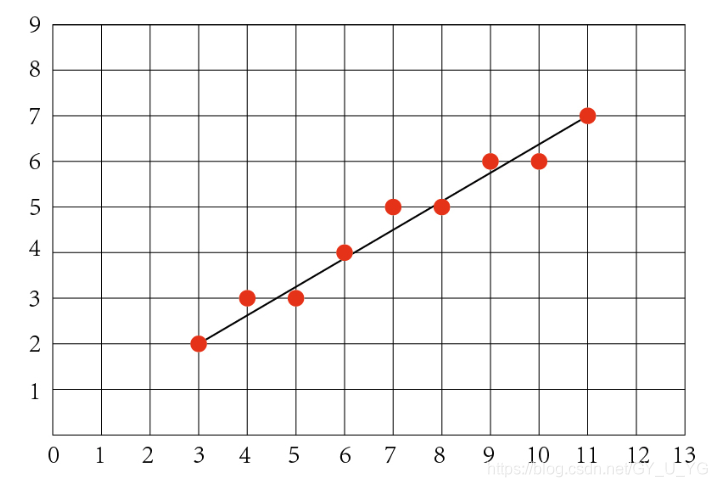
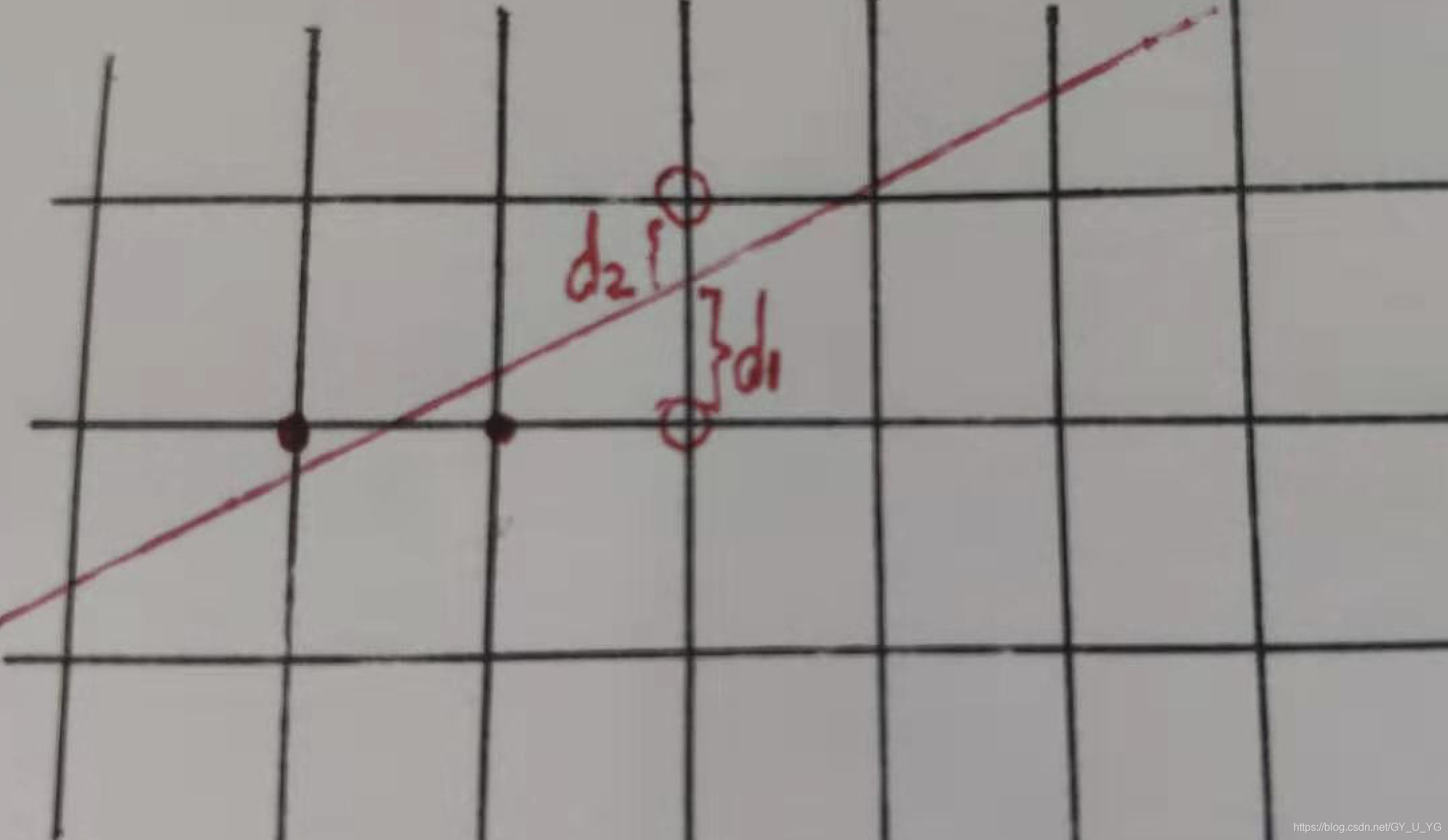
下面两张图只是说明在光栅显示屏上,直线并不是理想的直线,而是趋近于理想直线附近的像素点集合成一个点阵,看上去很接近直线
【这里需要一张dot.png的图】
十、DDA(Digital Differential Analyzer)数字微分法画线
采用了增量思想,增量思想是数学推导中十分重要的思想,大学中的微积分就是采用增量思想推导的。
DDA在本课题中画线思想非常容易理解,就是假定一个坐标轴,比如以x轴为方向,从起点x1 扫描(循环)到 终点x2,每次步进一个像素,根据直线公式计算出 y 的值,然后把对应的坐标(x, y)附近合适的像素点写入内存(显示在屏幕)即可
现在其实已经进入了真正的数学世界了。我们要具备一点点数学知识:
- 直线可以用 y = kx + b 表示
- 直线无论怎么平移,相同距离的增量是不会变的,比如 y = 2x + 5 和 y = 2x ,后者可以看做是前者向下平移5个单位而成的,这两条直线只要 x 增加 1,y 就增加 2,其实和后面的+5是没有关系的,也就是相同距离的增量和b是没有关系的
- 坐标系中 x 和 y 是轮换对称的 ,x 和 y 的地位是绝对相等的,x 可以看做是 y 的函数, y 也可以看做是 x 的函数,比如y = kx, 也可以写成 x = my,两者在坐标系地位相等(事实上,km = 1,两者互为倒数,因为同一个角的正切值和余切值互为倒数)
- 注意到斜率无穷大的情况,垂直直线。tan90是不存在的,无穷大。
在坐标系中直线通过平移,增量是不会变的,
思想描述:
- 已知直线的两个端点坐标:(x1, y1)和(x2, y2)
- 直线的颜色:color
- 计算两个方向的变化量:dx = x2 - x1;dy = y2 - y1;
- 求出两个方向的最大变化量的绝对值:steps = max(|dx|, |dy|)
- 计算了两个方向的增量(考虑了方向在内):xin = dx / steps; yin = dy / steps;
- 设置初始像素:x = x1; y = y1;
- 循环扫描写入像素点;
for (i = 1; i <= steps; i++) {
setPixel(round(x), round(y));
x += xin;
y += yin;
}
下面先给一个不考虑象限,不考虑斜率的简单写法,比如第一象限斜率为正数的一个简单情况:
void DDALine(int x1,int y1,int x2, int y2, int color) {
int x;
float dx, dy, y, k;
dx = x2 - x1;
dy = y2 - y1;
k = dy / dx;
y = y1;
for(x = x1; x <= x2; x++) {
setPixel(x, (int)(y + 0.5), color);
y = y + k;
}
}
下面给出一个轮换对称式通用写法:
void DDA(int x1, int y1, int x2, int y2, int color) {
float xin, yin;
float x = x1;
float y = y1;
int steps, i;
int dx = x2 - x1;
int dy = y2 - y1;
if (abs(dx) > abs(dy)) {
steps = abs(dx);
} else {
steps = abs(dy);
}
xin = (float)dx/steps;
yin = (float)dy/steps;
for (i = 1; i <= steps; i++) {
setPixel(round(x), round(y), color);
x += xin;
y += yin;
}
}
十一、中点画线法
中点画线法依旧采用了增量步进的思想,和DDA相比,DDA采用的 y = kx + b 斜截式,这种情况 k 很容易是浮点数,在扫描运算的过程中会设计到大量的浮点运算,前面我们已经讲过,机器做浮点运算消耗是很大的,效率远远不如做加法那么简单。所以,中点画线法不再采用斜截式,而是采用直线的一般式写法:ax + by + c = 0;
每次在 X轴 方向上扫描步进 一个像素, Y轴方向前进还是不前进取决于误差项判断。
【此处有图midline.png】
其数学思想就是在坐标系中看:
- 当一个点(xp, yp)在直线上方时,将该点代入直线的一般式方程,结果 大于 0;
- 当一个点(xp, yp)在直线下方时,将该点代入直线的一般式方程,结果 小于 0;
- 当一个点(xp, yp)经过该直线时,将该点代入直线的一般式方程,结果 等于 0;
假设线段的起点是(x1, y1),终点是(x2, y2),直线方程:Ax + By + C = 0;
其中:
- A = y1 - y2 = -dy
- B = x2 - x1 = dx
- C = x1y2 - x2y1
推导如下:
对于AX+BY+C=0:
当x1 = x2时,直线方程为x - x1 = 0
当y1 = y2时,直线方程为y - y1 = 0
当x1 ≠ x2,y1 ≠ y2时,直线的斜率k = (y2 - y1) / (x2 - x1)
故直线方程为y - y1 = (y2 - y1) / (x2 - x1)(x - x1)
即x2y - x1y - x2y1 + x1y1 = (y2 - y1)x - x1(y2 - y1)
即(y1 - y2)x - (x1 - x2)y - x1(y1 - y2) + (x1 - x2)y1 = 0
即(y1 - y2)x + (x2 - x1)y + x1y2 - x2y1 = 0… ①
可以发现,当 x1 = x2 或 y1 = y2 时,①式仍然成立。所以直线Ax + By + C = 0的一般式方程就是:
A = y1 - y2
B = x2 - x1
C = x1y2 - x2y1
为了简化各种情况,我们假设直线斜率 0 < k < 1,那么在 X轴 方向,x 每步进一个像素(步进为1),y 增加 不会超过1(斜率决定的),
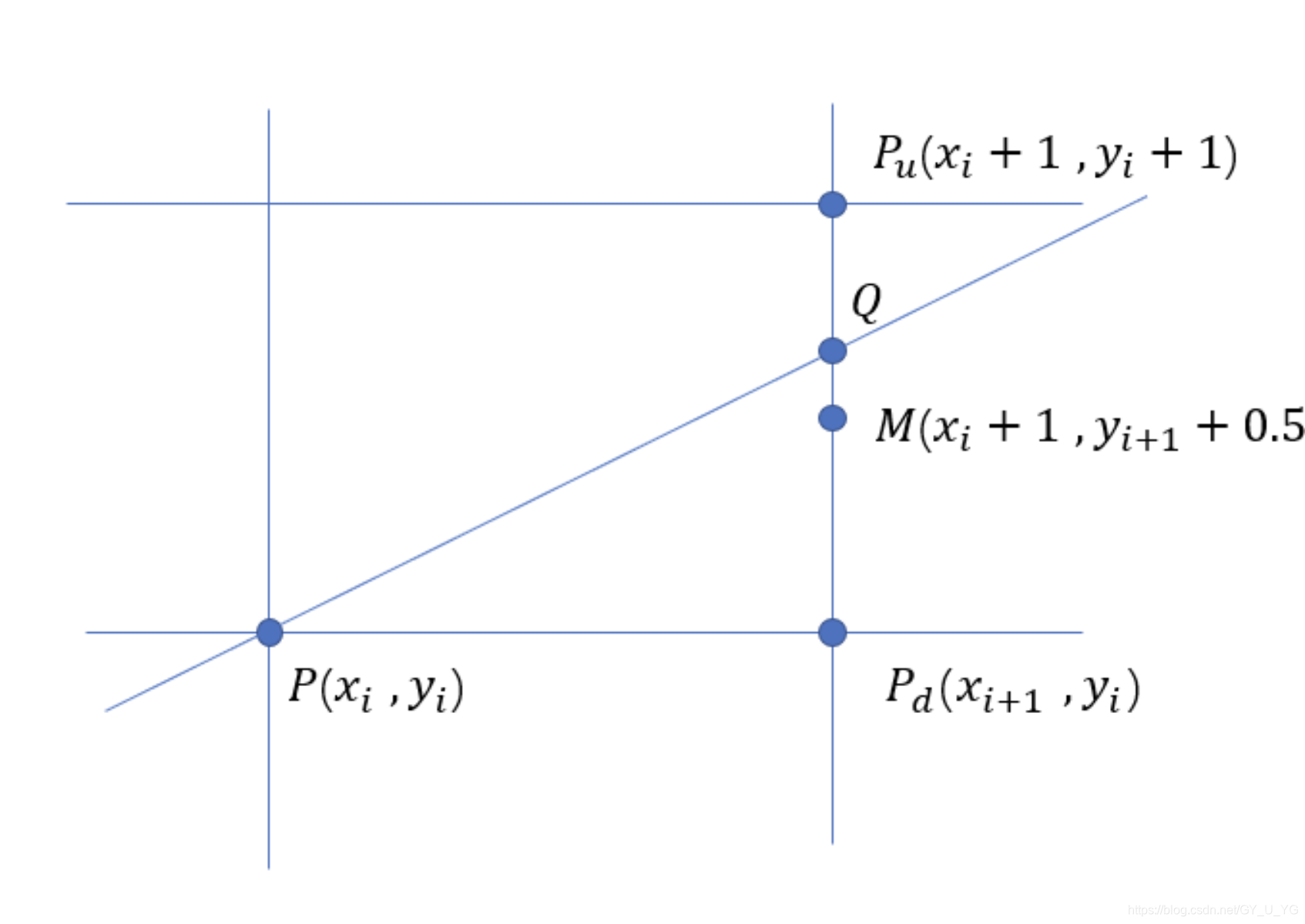
x 从 xi 步进到 xi+1,yi 处于yi 和 yi+1之间。
如图所示:理想直线经过的Q点处于Pu和Pd之间,我们肯定选择距离更近的像素点。如何判断哪个点才是理想点呢。这里,我们采用了中点法,也就是取 Pu和Pd的中点M(xi + 1, y1 + 0.5),代入直线方程,看结果是大于0,还是小于0,还是等于0,以此来判断M点是在理想直线之间的位置关系。
设 d = F(xi+1, yi + 0.5) = A(xi + 1) + B(yi + 0.5) + C
- d > 0,说明M点在理想直线上方,Q点距离Pd(xi+1, yi)更近,我们取Pd作为下一个像素点;
- d < 0,说明M点在理想直线下方,Q点距离Pu(xi+1, yi+1)更近,我们取Pu作为下一个像素点;
- d = 0,随便取一个,我们约定取Pd吧;
所以呢,yi+1和 yi之间的关系也就出来了:
- 如果d >= 0,yi+1 = yi
- 如果 d < 0, yi+1 = yi + 1
前面已经说了:
d = F(xi+1, yi + 0.5) = A(xi + 1) + B(yi + 0.5) + C
(1),若当前像素处于 d >= 0 情况,我们取Pd(xi + 1, yi),要判断下一个像素的位置,也就是要寻找下个中点,应该计算
d1 = F(xi + 2, yi + 0.5)
= A(xi + 2) + B(yi + 0.5) + C
= A(xi + 1) + B(yi + 0.5) + C + A
= d + A
我们发现此时增量为 A;
(2),若当前像素处于 d < 0 的情况,我们取Pu(xi + 1, yi + 1),要判断下一个像素点的位置,也就是要寻找下个中点,应该计算
d2 = F(xi + 2, yi + 1.5)
= A(xi + 2) + B(yi + 1.5) + C
= A(xi + 1) + B(yi + 0.5) + C + A + B
= d + A + B
我们发现此时的增量是 A + B;
也就是说,我们依次将步进过程中的中点代入理想直线方程,得到了一个递推关系;
di+1 = di + ?
- 如果 di >= 0,di+1 = di + A
- 如果di < 0,di+1 = di + A + B
我们画线从(x0, y0)开始,那么d的初始值:
- d0 = F(x0 + 1, y0 + 0.5)
= A(x0 + 1) + B(y0 + 0.5) + C
= Ax0 + By0 + C + A + 0.5B
= F(x0, y0) + A + 0.5B
= A + 0.5B
我们从繁杂的数学推导中抽出身来,认真的思考一下,d 对我们的意义就是要它的符号,正数还是负数,至于是多少还真是不太重要。因为计算机计算浮点运算是非常“费时低效”的,所以将d0乘以2,去浮点化,这样硬件操作就会更加高效快速,即 d0 = 2A + B,所以,增量也相应 A -> 2A,A + B -> 2(A + B)
那么问题就转化为:我们随着x的逐一递增,从d0到dk也存在着递推关系,我们根据每一步的di值,判断y方向是不是要 + 1,di的值决定我们要不要在y的方向上增加1,因此,我们称di为判别式,或者决策因子。
// 未做数学处理,含有浮点运算
void MidpointLine(int x1, int y1, int x2, int y2, int color) {
int a, b, d1, d2, x, y;
a = y1 - y2;
b = x2 - x1;
float d = a + 0.5 * b;
d1 = a;
d2 = a + b;
x = x1, y = y1;
setPixel(x, y, color);
while(x < x2) {
if (d < 0) {
x++;
y++;
d += d2;
} else {
x++;
d += d1;
}
setPixel(x, y, color);
}
}
void MidpointLine(int x1, int y1, int x2, int y2, int color) {
int a, b, d1, d2, d, x, y;
a = y1 - y2;
b = x2 - x1;
d = a << 1 + b;
d1 = a << 1;
d2 = (a + b) << 1;
x = x1, y = y1;
setPixel(x, y, color);
while(x < x2) {
if (d < 0) {
x++;
y++;
d += d2;
} else {
x++;
d += d1;
}
setPixel(x, y, color);
}
}
上面只是推导了k ∈ [0, 1]的情况,我这里又总结了 斜率为其他情况的递推公式,可以根据下表快速写出其他情况的C语言程序
十二、Bresenham画线算法
其实,从上面的中点画线法来看,效率已经达到了最佳,但是依旧不是很好,我们希望有一种算法可以根据任意形式的直线方程都可以画出直线,不仅仅是直线,还可以是圆弧,并且保持效率的最佳。于是IBM有个名叫Bresenham(布雷森汉姆)的工程师,在60年代给出了自己的算法。
其实和DDA思想一样,假设我们先考虑第一象限斜率也是 0 < k < 1的情况,其他情况推导方法类似,也就是数学中的分类讨论。
设直线从(x0, y0)开始,到(x1, y1)结束
- deltaX = x1 - x0
- deltaY = y1 - y0
- k = deltaY / deltaX
- 假设 0<k<1
- 第 i 个像素坐标(xi, yi)
- 则下一个像素点坐标只能为(xi+1, yi) 或者 (xi+1, yi+1)
下面是一些推导:
就这样我们得出了 Pi+1 和 Pi 的递推关系,我们称Pi为判断下一像素点的决策因子。
既然有了递推关系,那么按照数学的惯例,我们需要求出P0,也就是初始值。
需要计算的几个量,假设起点是s(x0, y0),终点是e(x1, y1)
- deltaX = x1 - x0
- deltaY = y1 - y0
- P0 = 2 * deltaX - deltaY
- delta1 = 2 * deltaY
- delta2 = 2 * deltaY - 2 * deltaX
绘点过程:
- 绘制起点s;
- 若P0 >= 0,则下一个点是(x0+1, y0+1),P1 = P0 + delta2;若P0 < 0,则下一个点是(x0+1, y0),P1 = P0 + delta1;
- 重复步骤2,对于(xk, yk),若Pk >= 0,则下个点(xk+1, yk+1),Pk+1 = Pk + delta2;若Pk < 0,则下个点是(xk+1, yk),Pk+1 = Pk + delta1;
- 循环到 x = x1,算法终止
接下来考虑斜率大于1的情况,因为x,y是轮换对称的,我们可以交换x,y,并做类似推导,此处略。
最后就是斜率小于0的情况,具体的实施方案就是将线段关于Y轴对称,则斜率为正,也就是将起始点和终点横坐标都取反,纵坐标不变,得到的每个点在画点的时候只要将横坐标取反即可。
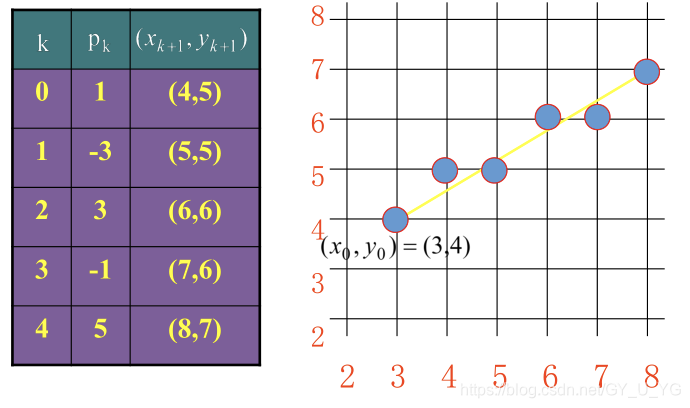
例如,我们举个例子(3, 4) -> (8, 7):
void bresenhamLine(int x0, int y0, int x1, int y1) {
int deltaX = x1 - x0;
int deltaY = y1 - y0;
int P = (deltaY << 1) - deltaX;
int delta1 = deltaY << 1;
int delta2 = (deltaY - deltaX) << 1;
int x = x0;
int y = y0;
while (x <= x1) {
cout << x << ", " << y << endl;
if (P >= 0) {
x++;
y++;
P += delta2;
} else {
x++;
P += delta1;
}
}
}
十三、圆弧的绘制算法
圆弧的绘制算法也有中点算法和bresenham算法,前面我们讲了直线的算法,有了直线,我们就可以绘制各种矩形、三角形、多边形等等,有了弧线,我们就可以绘制各种曲线,圆角矩形等等。
在平面解析几何中,圆的方程可以描述为(x – x0)2 + (y – y0)2 = R2,其中(x0, y0)是圆心坐标,R是圆的半径,特别的,当(x0, y0)就是坐标中心点时,圆方程可以简化为x2 + y2 = R2。在计算机图形学中,圆和直线一样,也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的圆的生成,对于中心不是原点的圆,可以通过坐标的平移变换获得相应位置的圆。
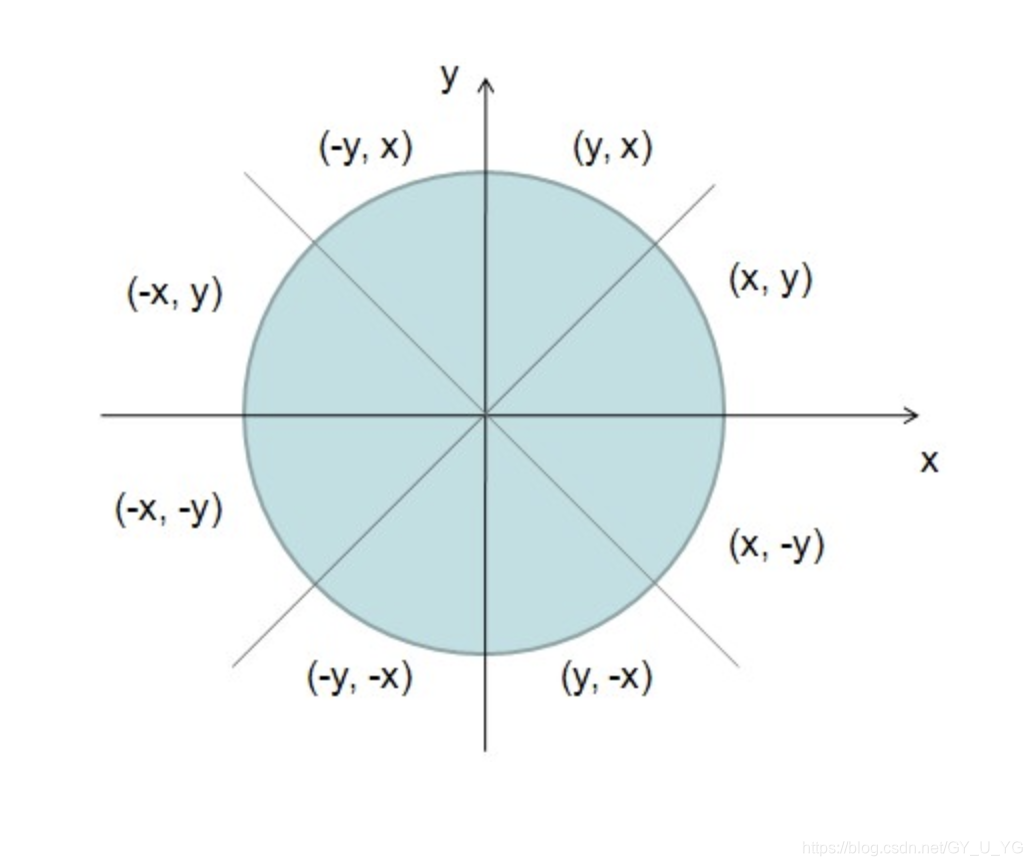
要特别关注圆的四条对称轴,x轴、y轴、y = x, y = -x ,圆的八分对称性,所以,我们只要画出八分之一个圆的圆弧,通过对称就可以画出整个圆,这里我们就讲讲从(0, R) 到 (R’, R’)也就是与y=x相交的位于 第一象限 上半段圆弧,占整个圆的八分之一。
这里需要一个图
联想到我们之前的中点划线法,这里还是采用一样的方式。顺时针x方向每次步进一个像素,看看y需不需要变化(减少)一个像素。
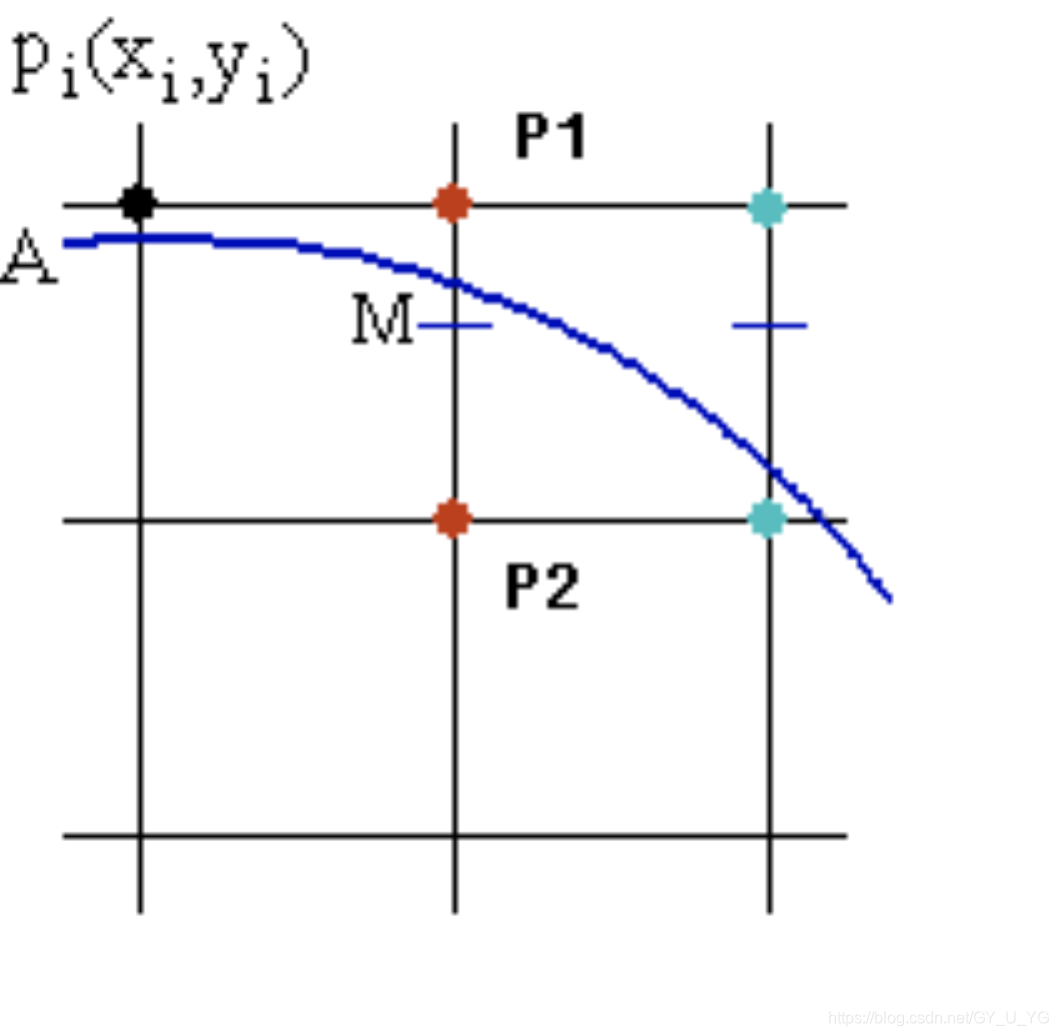
现在我们假设Pi(xi, yi)就是我们理想圆上的或者最接近理想圆的我们已经选择的第i个像素点。那么下一个点Pi+1一定会在上图中的P1 或者 P2 中选择。相同的套路,我们依旧选择M点作为线段P1P2的中点。
- 如果一个点在圆内,代入圆的方程,小于 0;
- 如果一个点在圆外,代入圆的方程,大于 0;
- 如果一个点在圆上,代入圆的方程,等于 0;
我们把M(xi+1, yi-0.5)代入圆的方程,如果大于0,说明M点在圆外,我们选择更近的P2(xi+1, yi-1)作为下一个点Pi+1,y方向上变化成功;如果小于0,说明M点在圆内,我们选择更近的P1(xi+1, yi)作为下一个点Pi+1,y方向上没有变化。
圆的方程:
F(x, y) = x2 + y2 - R2
现在将M点坐标(xi + 1, yi – 0.5)带入判别函数F(x, y),得到判别式d,也叫决策因子:
d = F(xi + 1, yi – 0.5)= (xi + 1)2 + (yi – 0.5)2 – R2
- 若d < 0,则取P1为下一个点,此时P1(xi+1, yi)的下一个点的判别式为:d’ = F(xi + 2, yi – 0.5)= (xi + 2)2 + (yi – 0.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2xi + 3 - 若d > 0,则取P2为下一个点,此时P2(xi+1, yi-1)的下一个点的判别式为:d’ = F(xi + 2, yi – 1.5)= (xi + 2)2 + (yi – 1.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2(xi - yi) + 5 - 特别的,在第一个象限的第一个点(0, R)时,可以推倒出判别式d的初始值d0:
d0 = F(1, R – 0.5) = 1 – (R – 0.5)2 – R2 = 1.25 - R
计算过程如下图:
现在初始值有了,决策因子的递推关系也出来了:
- d0 = 1.25 - R;
- d < 0时,则 d1+1 = di + 2 * x1 + 3;
- d >=0时,则 di+1 = di + 2 *(xi - yi) + 5;
话不多说,直接上代码:
void arc(int r) {
int x,y;
double d;
x = 0, y = r;
d = 1.25 - r;
while (x < y) {
if (d < 0) {
d = d + 2*x + 3;
} else {
d = d + 2*(x-y) + 5;
y--;
}
cout << "(" << x << ", " << y <<")" << endl;
// pic[y][x] = true;
// 给相应的点着色
SetPixel(x, y, color)
x++;
}
}
有了之前的基础,我们一眼就识别出上面这段代码的不足之处,有个浮点,而且这个浮点被带入循环,不利于机器执行所以,我们想办法要去掉浮点,提高效率。
其实,我们的目的很简单,就是随着x不断的步进,y是否也能在x步进的每一步跟着步进或者保持不动。至于我们计算推导过程中的决策因子d,我们要的只是它的符号,只要保持它的符号不变即可,x,y和决策因子之间并没有直接的运算关系。
我们可以将初始值d = 1.25 - r乘以2,得到 d = 2.5 - 2r,因为我们这里每次步进都是一个像素,不存在半个或者零点几个像素,所以2.5改成3,也是不影响的,所以令 d = 3 - 2r,每次和d相加减的delta增量也乘以2,就像 a + b > 0, 那么 2a + 2b 肯定也大于零。
其实,可以直接乘以4,这样d的值直接就变成 5 - 4r 了。那么相应的低增值也要乘以4,维持符号不变即可。
void arc(int r) {
int x, y, d;
x = 0, y = r;
d = 3 - 2 * r;
while (x < y) {
if (d < 0) {
d = d + (x << 2) + 6;
} else {
d = d + ((x-y) << 2) + 10;
y--;
}
cout << "(" << x << ", " << y <<")" << endl;
// pic[y][x] = true;
// 给相应的点着色
SetPixel(x, y, color)
x++;
}
}
或者如下:
void arc(int r) {
int x, y, d;
x = 0, y = r;
d = 5 - 4 * r;
while (x < y) {
if (d < 0) {
d = d + (x << 3) + 12;
} else {
d = d + ((x-y) << 3) + 20;
y--;
}
cout << "(" << x << ", " << y <<")" << endl;
// pic[y][x] = true;
// 给相应的点着色
SetPixel(x, y, color)
x++;
}
}