线性回归
-
回归问题
输入变量和输出都是连续的问题 -
一维线性问题
-
模型选择
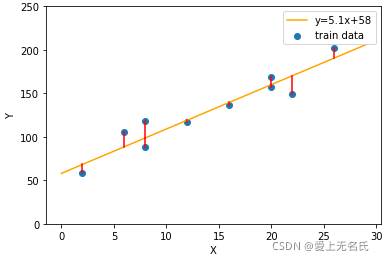
y = w x + b y = wx + b y=wx+b -
损失函数 (表示预测值和数据真实值的偏差)
L ( y , y i ) = ∑ i = 1 n ( y − y i ) 2 L(y,y_i) = \sum_{i=1}^n (y - y_i)^2 L(y,yi)=i=1∑n(y−yi)2
损失函数使用的是均值误差(定义为图中 预测值(黄线) 和 真实值(蓝点)的距离的平方)。还可以为,曼哈顿距离,马氏距离,总偏差平方和,回归平方和,残差平方和等 -
求解
求解斜率w和截距b。既可以得到一维线性方程。 损失函数最小值则表示训练数据整体和真实数据的距离最小。此时的预测值越接近真实值。-
对b 偏导数
∂ f ∂ b = − 2 ( ∑ i = 1 n y i − n b − w ∑ i = 1 n x i ) \frac{\partial f}{\partial b} = -2(\sum_{i=1}^n y_i -nb - w\sum_{i=1}^n x_i) ∂b∂f=−2(i=1∑nyi−nb−wi=1∑nxi) -
对w 偏导数
∂ f ∂ w = − 2 ( ∑ i = 1 n y i ∗ x i − ∑ i = 0 n x i − w ∑ i = 1 n x i ) \frac{\partial f}{\partial w} = -2(\sum_{i=1}^n y_i * x_i -\sum_{i=0}^n x_i - w\sum_{i=1}^n x_i) ∂w∂f=−2(i=1∑nyi∗xi−i=0∑nxi−wi=1∑nxi)
-
令 ∂ f ∂ w = 0 \frac{\partial f}{\partial w}=0 ∂w∂f=0 以及 ∂ f ∂ b = 0 \frac{\partial f}{\partial b}=0 ∂b∂f=0
w = n Σ y i ∗ x i − Σ x i ∗ Σ y i n Σ x i 2 − ( Σ x i ) 2 w = \frac{n\varSigma y_i * x_i -\varSigma x_i*\varSigma y_i}{n\varSigma x_i^2 -(\varSigma x_i)^2} w=nΣxi2−(Σxi)2nΣyi∗xi−Σxi∗Σyi
b = Σ x i 2 ∗ Σ y i − Σ x i ∗ Σ y i x i n Σ x i 2 − ( Σ x i ) 2 b = \frac{\varSigma x_i^2 *\varSigma y_i -\varSigma x_i*\varSigma y_i x_i}{n\varSigma x_i^2 -(\varSigma x_i)^2} b=nΣxi2−(Σxi)2Σxi2∗Σyi−Σxi∗Σyixi
==>
w = X ‾ ∗ Y ‾ − ( X Y ) ‾ X ‾ 2 − X 2 ‾ w = \frac{\overline{X} * \overline{Y} - \overline{(XY)}}{\overline{X}^2 - \overline{X^2}} w=X2−X2X∗Y−(XY)b = Y ‾ − w X ‾ b = \overline{Y} - w\overline{X} b=Y−wX
-
-
-
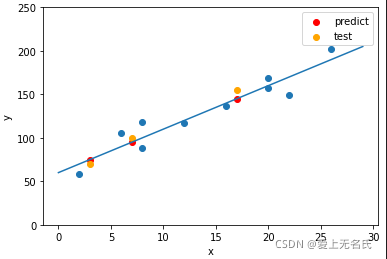
编程验证1:手动实现
import numpy as np import matplotlib.pyplot as plt #测试数据 train_x = np.array([2, 6, 8, 8, 12, 16, 20, 20, 22, 26]) train_y = np.array([58, 105, 88, 118, 117, 137, 157, 169, 149, 202]) #测试数据 test_x = np.array([3, 7, 17]).reshape(-1, 1) test_y = np.array([70, 100, 155]).reshape(-1, 1) class OneLineaRegression: def __init__(self, train_x, train_y): self.train_x = train_x self.train_y = train_y self.train = np.hstack( (train_x.reshape(-1, 1), train_y.reshape(-1, 1))) self.w = 0 self.b = 0 def calcuate_loss(self): #计算线性参数 w ,b # x 均值 x_avg = np.mean(self.train_x) # y 均值 y_avg = np.mean(self.train_y) # x*y的均值 xy_avg = np.mean(self.train_x * self.train_y) # 平方的均值 xx_avg = np.mean(self.train_x ** 2) # 均值的平方 x_avg_x = x_avg * x_avg self.w = (x_avg * y_avg - xy_avg) / (x_avg_x - xx_avg) self.b = y_avg - self.w * x_avg def predict(self, x): return self.w * x + self.b def show_line(self, pre_value): line_x = np.arange(0, 30) line_y = self.w * line_x + self.b plt.scatter(self.train_x, self.train_y) plt.plot(line_x, line_y,label='y = %.2fx + %.2f' % (self.w, self.b)) plt.xlabel('x') plt.ylabel('y') plt.ylim(0, 250) # 预测值 test_pre_y = self.predict(test_x) plt.scatter(test_x, test_pre_y,c='r',label='predict') plt.scatter(test_x, test_y,c='orange',label='test') plt.legend() plt.legend() plt.show() # 测试 model = OneLineaRegression(train_x, train_y) # 训练数据 model.calcuate_loss() # 显示一维显示方程参数 print("一维线性回归:",'斜率:',model.w,' 截距:',model.b) # 一维线性回归: 斜率: 5 截距: 60 # 预测并显示 model.show_line() -
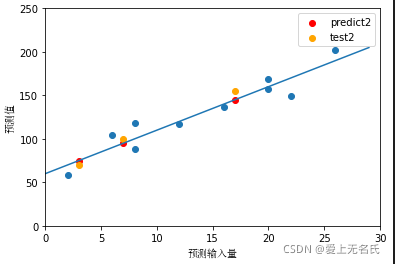
编程实现2:sklearn 机器学习包
from sklearn.linear_model import LinearRegression import matplotlib.pyplot as plt # 和方式1 一样的训练数据 train_x = np.array([2, 6, 8, 8, 12, 16, 20, 20, 22, 26]).reshape((-1, 1)) train_y = np.array([58, 105, 88, 118, 117, 137, 157, 169, 149, 202]).reshape((-1, 1)) # sklearn 提供的线性回归函数 model = LinearRegression() #训练数据 model.fit(train_x, train_y) # 画图 def show_line(w, b): line_x = np.arange(0, 30) line_y = w * line_x + b pre_value = w * pre_x + b plt.plot(line_x, line_y) plt.scatter(train_x, train_y) plt.xlabel('预测输入量',fontproperties="SimSun") plt.ylabel('预测值',fontproperties="SimSun") plt.ylim(0, 250) plt.xlim(0, 30) test_pre_y = model.predict(test_x) plt.scatter(test_x, test_pre_y,c='r',label='predict2') plt.scatter(test_x, test_y,c='orange',label='test2') plt.show() print('线性回归函数参数:', '斜率:', model.coef_[0, 0], ',截距:', model.intercept_[0]) #线性回归函数参数: 斜率: 5.0 ,截距: 60.0 show_line(model.coef_[0, 0], model.intercept_[0] )
- 一元多项式预测函数
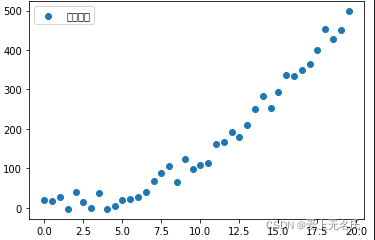
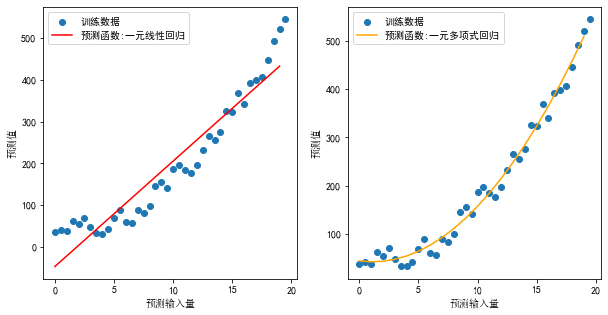
- 数据并非一元线性方程,数据走向适合二次项,三次项
- 多项式模型选择 y = β 0 + β 1 ∗ x + β 2 ∗ x 2 + β 3 ∗ x 3 + β 4 ∗ x 4 + β 5 ∗ x 5 + b y=\beta_0 +\beta_1 * x+ \beta_2 * x^2+ \beta_3 * x^3+ \beta_4 * x^4+ \beta_5 * x^5 + b y=β0+β1∗x+β2∗x2+β3∗x3+β4∗x4+β5∗x5+b
- 例如该数据如果用一元线性方程不能切合所有数据,而更适合二项式函数
- 一元多项式
# 模拟一元多项式回归 from sklearn.preprocessing import StandardScaler, MaxAbsScaler from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression import numpy as np import matplotlib.pyplot as plt plt.rcParams['font.family'] = ['SimHei'] # 生成模拟数据 y = 10.5 - 2.4 *x + 1.4 * x^2 + 30 impurity_x = np.arange(0, 20, 0.5).reshape(-1, 1) impurity_y = 10.5 - 2.4 * impurity_x + 1.4 * impurity_x ** 2 + 30 + np.random.uniform(-30, 30, impurity_x.shape) train_x = impurity_x[:, :] train_y = impurity_y[:, :] # 一元线性回归 def showLine1(): plt.subplot(121) plt.scatter(train_x, train_y, label='训练数据') # 一元线性回归 model = LinearRegression() model.fit(train_x, train_y) line_x = np.arange(0, 20, 1).reshape(-1, 1) line_y = model.predict(line_x) plt.plot(line_x, line_y, label='预测函数:一元线性回归', c='r') plt.xlabel('预测输入量', fontproperties="SimSun") plt.ylabel('预测值', fontproperties="SimSun") plt.legend() #一元多项式回归 def showLine2(): plt.subplot(122) # 一元多项式回归 # 生成二次项特征值 quad_model = PolynomialFeatures(degree=2) train_x_quad = quad_model.fit_transform(train_x) model2 = LinearRegression() model2.fit(train_x_quad, train_y) test_x = np.arange(0, 20, 1).reshape(-1, 1) quad_test_x = quad_model.fit_transform(test_x) test_y = model2.predict(quad_test_x) plt.scatter(train_x, train_y, label='训练数据') plt.plot(test_x, test_y, label='预测函数:一元多项式回归', c='orange') plt.xlabel('预测输入量', fontproperties="SimSun") plt.ylabel('预测值', fontproperties="SimSun") plt.legend() plt.figure(figsize=(10, 5)) showLine1() showLine2() plt.show()