数据结构（三）—— 树（3）：二叉树的遍历

数据结构系列内容的学习目录 $\rightarrow$ 浙大版数据结构学习系列内容汇总。

3. 二叉树的遍历

3. 二叉树的遍历

3.1 二叉树的递归遍历

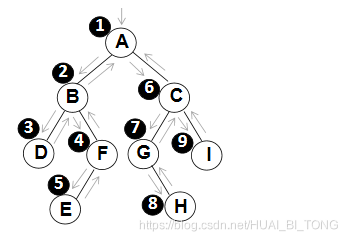
(1）先序遍历
遍历过程为：1. 访问根结点；
2. 先序遍历其左子树；
3. 先序遍历其右子树。

void PreOrderTraversal(BinTree BT)
{
    if(BT) {
        cout << BT->Data << endl;
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BP->Right);
    }
}

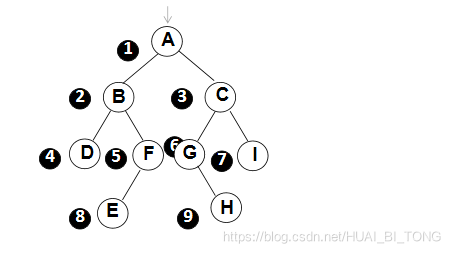
在这里插入图片描述
上图所示的二叉树先序遍历顺序：A B D F E C G H I。

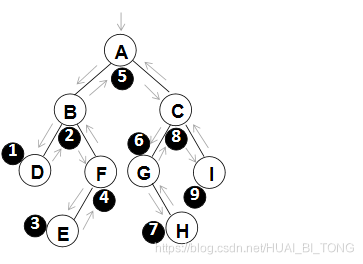
(2）中序遍历
遍历过程为：1. 中序遍历其左子树；
2. 访问根结点；
3. 中序遍历其右子树。

void InOrderTraversal(BinTree BT)
{
    if(BT){
        InOrderTraversal(BT->Left);
        cout << BT->Data << endl;
        InOrderTraversal(BT->Right);
    }
}

在这里插入图片描述
上图所示的二叉树中序遍历顺序：D B E F A G H C l。

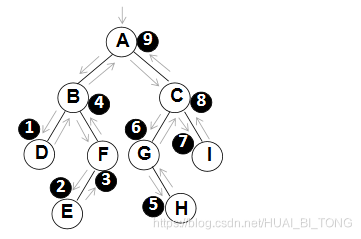
(3）后序遍历
遍历过程为：1. 后序遍历其左子树；
2. 后序遍历其右子树；
3. 访问根结点。

void PostOrderTraversal(BinTree BT)
{
    if(BT){
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        cout << BT->Data << endl;
    }
}

在这里插入图片描述
上图所示的二叉树后序遍历顺序：D E F B H G I C A。

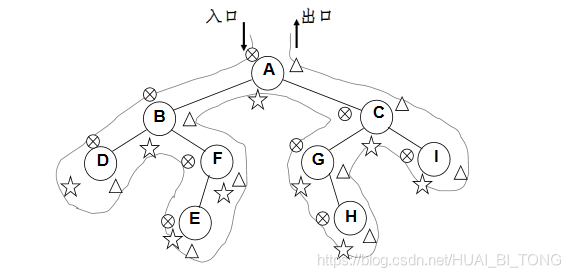
先序、中序和后序遍历过程： 遍历过程中经过结点的路线一样，只是访问各结点的时机不同。
下图中在从入口到出口的曲线上用 $\otimes$ 、 $☆$ 和 $△$ 三种符号分别标记出了先序、中序和后序访问各结点的时刻。

在这里插入图片描述

3.2 二叉树的非递归遍历

非递归算法实现的基本思路：使用堆栈。

(1）中序遍历的非递归遍历算法
遍历过程为：1. 遇到一个结点，就把它压栈，并去遍历它的左子树；
2. 当左子树遍历结束后，从栈顶弹出这个结点并访问它；
3. 然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal(BinTree BT)
{
    BinTree T=BT;
    Stack S = CreatStack(Maxsize);  //创建并初始化堆栈S
    while( T || !IsEmpty(S)){
        while(T){  //—直向左并将沿途结点压入堆栈
            Push(s, T);
            T = T->Left;
        }
        if(!IsEmpty(S)){
            T = Pop (S);  //结点弹出堆栈
            cout << T->Data << endl;  //(访问）打印结点
            T = T->Right;  //转向右子树
        }
    }
}

(2）先序遍历的非递归遍历算法

void PreOrderTraversal(BinTree BT)
{
	BinTree T = BT;
	Stack S = CreateStack();  //创建并初始化堆栈S
	while(T || !IsEmpty(S)){  //当树不为空或堆栈不空 
		while(T){     
			Push(S,T);    //压栈，第一次遇到该结点 
			cout << T->Data << endl;  //(访问）打印结点
			T = T->Left;   //遍历左子树 
		}
		if(!IsEmpty(S)){  //当堆栈不空 
			T = Pop(S);    //出栈，第二次遇到该结点 
			T = T->Right;  //访问右结点 
		}
	} 
}

(3）后序遍历的非递归遍历算法

void PostOrderTraversal(BinTree BT)
{
	BinTree T = BT;
	Stack S = CreateStack();  //创建并初始化堆栈S
	vector<BinTree> v;   //创建存储树结点的动态数组
	Push(S,T);
	while(!IsEmpty(S)){  //当树不为空或堆栈不空 
		T = Pop(S);
		v.push_back(T);  //出栈元素进数组
		if(T->Left)
			Push(S,T->Left);
		if(T->Right)
			Push(S,T->Right);
	}
	reverse(v.begin(),v.end());  //逆转 
	for(int i=0;i<v.size();i++)  //输出数组元素
		cout << v[i]->Data << endl;
}

3.3 层序遍历

层序遍历的遍历过程： 从上至下，从左至右访问所有结点。

二叉树遍历的核心问题：二维结构的线性化。
$\diamond$ 从结点访问其左、右子结点
$\diamond$ 访问左子结点后，右子结点怎么办?
$\bullet$ 需要一个存储结构保存暂时不访问的结点
$\bullet$ 存储结构：堆栈、队列

队列实现： 遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右子结点入队。

在这里插入图片描述
上图所示的二叉树层序遍历顺序：A B C D F G I E H。

层序基本过程： 先根结点入队，然后，1. 从队列中取出一个元素；
2. 访问该元素所指结点；
3. 若该元素所指结点的左、右子结点非空，则将其左、右子结点的指针顺序入队。

void LevelOrderTraversal(BinTree BT)
{
    Queue Q;
    BinTree T;
    if (!BT) 
        return;  //若是空树则直接返回
    Q = CreatQueue(Maxsize);  //创建并初始化队列
    AddQ(Q, BT);
    while(!IsEmptyQ(Q)){
        T = DeleteQ(Q);
        cout << T->Data << endl;  //访问取出队列的结点
        if(T->Left)
            AddQ(Q, T->Left);
        if(T->Right)
            AddQ(Q, T->Right);
    }
}

3.4 二叉树遍历的应用实例

例1： 遍历二叉树的应用，输出二叉树中的叶子结点。

在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。

void PreOrderPrintLeaves(BinTree BT)
{
    if(BT){
        if (!BT->Left && !BT->Right)  //左右子树都为空
            cout << BT->Data << endl;
        PreOrderPrintLeaves(BT->Left);
        PreOrderPrintLeaves(BT->Right);
    }
}

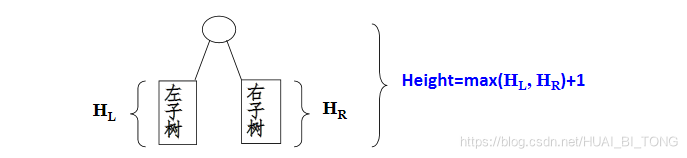
例2： 求二叉树的高度。

在这里插入图片描述

int PostOrderGetHeight(BinTree BT)
{
    int HL,HR,MaxH;
    if(BT){
        HL = PostOrderGetHeight(BT->Left);  //求左子树的深度
        HR = PostOrderGetHeight(BT->Right);  //求右子树的深度
        MaxH = (HL > HR) ? HL : HR;  //取左右子树较大的深度
        return (MaxH +1);  //返回树的深度
    }
    else 
        return 0;  //空树深度为0
}

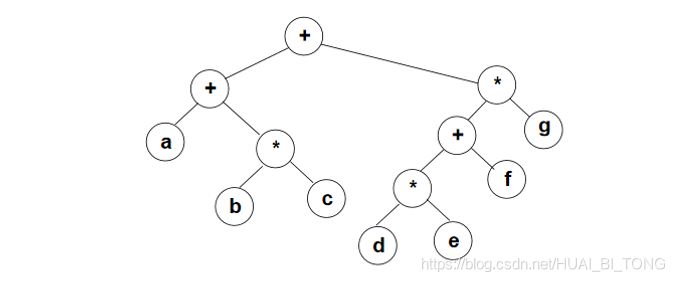
例3： 二元运算表达式树及其遍历。

在这里插入图片描述
三种遍历可以得到三种不同的访问结果：
$\diamond$ 先序遍历得到前缀表达式： $a * b \ _{} c*+*d\ _{} e\ _{}f \ _{}g$
$\diamond$ 中序遍历得到中缀表达式： $a + b * c + d * e + f * g$
$\diamond$ 后序遍历得到后缀表达式： $a \ _{}b\ _{} c * +d \ _{}e * f +g *+$

其中，中缀表达式会受到运算符优先级的影响。

例4： 由两种遍历序列确定二叉树。

问题：已知三种遍历中的任意两种遍历序列，能否唯一确定一棵二叉树呢?
答案：必须要有中序遍历才行！

在这里插入图片描述
没有中序的困扰：上图所示的两个二叉树的先序遍历序列：A B
后序遍历序列：B A

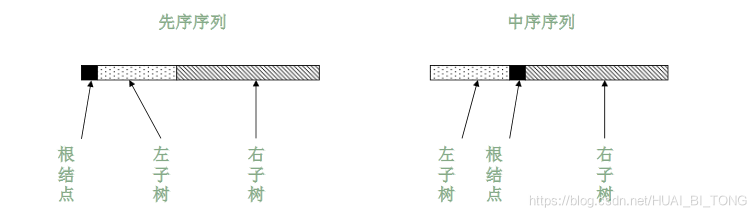
先序和中序遍历序列来确定一棵二叉树：
分析：1. 根据先序遍历序列第一个结点确定根结点；
2. 根据根结点在中序遍历序列中分割出左右两个子序列；
3. 对左子树和右子树分别递归使用相同的方法继续分解。

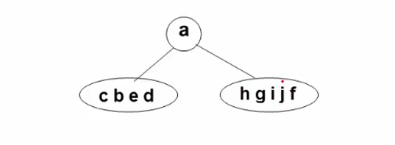
在这里插入图片描述
例如，先序序列：a b c d e f g h i j
中序序列：c b e d a h g i j f

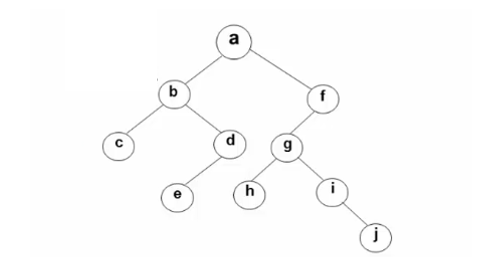
从先序序列可知第一个结点a为根节点，则中序序列a结点前面的结点c b e d均为左子树的中序序列，中序序列a结点后面的结点h g i j f 均为右子树的中序序列。

在这里插入图片描述
再去先序序列中寻找左子树中序序列c b e d对应的这4个结点的先序序列，就可知左子树的先序序列b c d e及其中序序列c b e d。

在这里插入图片描述
然后去先序序列中寻找右子树中序序列h g i j f 对应的这5个结点的先序序列，就可知右子树的先序序列 f g h i j 及其中序序列 h g i j f。

在这里插入图片描述
类似地，后序和中序遍历序列也可以确定一棵二叉树。

例5： 二叉树的链表存储实现。

二叉树的链表存储实现实例的代码如下所示。

#include<iostream>
using namespace std;
#include<vector> 
#include<queue>
#include<algorithm>

typedef struct TreeNode *BinTree;
struct TreeNode {
	int Data;  // 存值 
	BinTree Left;    // 左儿子结点 
	BinTree Right;   // 右儿子结点 
};
BinTree CreatBinTree();   // 创建一个二叉树
void  PreOrderTraversal_Recursion(BinTree BT);  // 先序递归遍历
void PreOrderTraversal(BinTree BT);   // 先序遍历，根左右
void InOrderTraversal_Recursion(BinTree BT);  // 中序递归遍历
void InOrderTraversal(BinTree BT);    // 中序遍历，左根右
void PostOrderTraversal_Recursion(BinTree BT);  // 后序递归遍历
void PostOrderTraversal(BinTree BT);  // 后序遍历，左右根 

typedef struct SNode *Stack;
struct SNode {
	BinTree Data;
	Stack Next;
};


Stack CreateStack();  // 初始化链栈 
int IsEmpty(Stack S);  // 判断链栈是否为空 
void Push(Stack S, BinTree item);  // 入栈 
BinTree Pop(Stack S);  // 出栈


// 初始化 
Stack CreateStack() 
{
	Stack S;
	S = (Stack)malloc(sizeof(struct SNode));
	S->Next = NULL;
	return S;
}

// 判断是否为空 
int IsEmpty(Stack S) 
{
	return (S->Next == NULL);
}

// 入栈
void Push(Stack S, BinTree item) 
{
	Stack tmp;
	tmp = (Stack)malloc(sizeof(struct SNode));
	tmp->Data = item;
	// 链栈栈顶元素是链表头结点，新入栈的链表在栈顶元素后面 
	tmp->Next = S->Next;
	S->Next = tmp;
}

// 出栈
BinTree Pop(Stack S) 
{
	Stack First;
	BinTree TopVal;
	if (IsEmpty(S)) 
	{
		cout << "堆栈空" << endl;
		return 0;
	}
	else 
	{
		First = S->Next;   // 出栈第一个元素在栈顶元素后面 
		S->Next = First->Next;  //把第一个元素从链栈删除 
		TopVal = First->Data;   // 取出被删除结点的值 
		free(First);  // 释放空间 
		return TopVal;
	}
}

BinTree Insert(int Data) 
{
	BinTree BT;
	BT = (BinTree)malloc(sizeof(struct TreeNode));
	BT->Data = Data;
	BT->Left = NULL;
	BT->Right = NULL;
	return BT;
}

// 初始化二叉树 
BinTree CreatBinTree() 
{
	BinTree BT;
	BT = (BinTree)malloc(sizeof(struct TreeNode));
	return BT;
}

// 先序递归
void  PreOrderTraversal_Recursion(BinTree BT)
{
	if(BT){
		cout << BT->Data;  // 打印根
		PreOrderTraversal_Recursion(BT->Left);  // 进入左子树
		PreOrderTraversal_Recursion(BT->Right);  // 进入右子树
	}
} 

// 先序非递归 
void PreOrderTraversal(BinTree BT) 
{
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while (T || !IsEmpty(S)) {  // 当树不为空或堆栈不空 
		while (T) {
			Push(S, T);    // 压栈，第一次遇到该结点 
			cout << T->Data;  // 访问结点
			T = T->Left;   // 遍历左子树 
		}
		if (!IsEmpty(S)) {  // 当堆栈不空 
			T = Pop(S);    // 出栈，第二次遇到该结点 
			T = T->Right;  // 访问右结点 
		}
	}
}

// 中序递归 
void InOrderTraversal_Recursion(BinTree BT)
{
	if(BT){
		InOrderTraversal_Recursion(BT->Left);  // 进入左子树
		cout << BT->Data;  // 打印根
		InOrderTraversal_Recursion(BT->Right);  // 进入右子树
	}
} 

// 中序非递归
void InOrderTraversal(BinTree BT) 
{
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while (T || !IsEmpty(S)) {  // 当树不为空或堆栈不空 
		while (T) {
			Push(S, T);    // 压栈
			T = T->Left;   // 遍历左子树 
		}
		if (!IsEmpty(S)) {  // 当堆栈不空 
			T = Pop(S);    // 出栈
			cout << T->Data;  // 访问结点
			T = T->Right;  // 访问右结点 
		}
	}
}

// 后序递归
void PostOrderTraversal_Recursion(BinTree BT)
{
	if(BT)
	{
		PostOrderTraversal_Recursion(BT->Left);  // 进入左子树
		PostOrderTraversal_Recursion(BT->Right);  // 进入右子树
		cout << BT->Data;  // 打印根
	}
} 

// 后序遍历 
void PostOrderTraversal(BinTree BT) 
{
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	vector<BinTree> v;
	Push(S, T);
	while (!IsEmpty(S)) {  // 当树不为空或堆栈不空 
		T = Pop(S);
		v.push_back(T);
		if (T->Left)
			Push(S, T->Left);
		if (T->Right)
			Push(S, T->Right);
	}
	reverse(v.begin(), v.end());  // 逆转 
	for (int i = 0; i < v.size(); i++)
	    cout << v[i]->Data;
}

// 层次遍历
void LevelOrderTraversal(BinTree BT) 
{
	queue<BinTree> q;
	BinTree T;
	if (!BT)
		return;
	q.push(BT);  // BT 入队 
	while (!q.empty()) {
		T = q.front();  // 访问队首元素 
		q.pop();  // 出队
		cout << T->Data;
		if (T->Left)
			q.push(T->Left);
		if (T->Right)
			q.push(T->Right);
	}
}
// 输出叶子结点
void  FindLeaves(BinTree BT) 
{
	if (BT) 
	{
		if (!BT->Left && !BT->Right)
			cout << BT->Data;  // 打印叶子结点
		FindLeaves(BT->Left);  // 进入左子树 
		FindLeaves(BT->Right);  // 进入右子树 
	}
}

// 求树高度
int  GetHeight(BinTree BT) 
{
	int HL, HR, MaxH;
	if (BT) {
		HL = GetHeight(BT->Left);  // 求左子树高度 
		HR = GetHeight(BT->Right);  // 求右子树高度 
		MaxH = (HL > HR) ? HL : HR;
		return MaxH + 1;  // 当前结点高度为左右子树最大的高度+1 
	}
	else
		return 0;
}
int main() 
{
	BinTree BT;
	BT = CreatBinTree();
	BT->Data = 1;
	BT->Left = Insert(2);
	BT->Right = Insert(3);
	BT->Left->Left = Insert(4);
	BT->Left->Right = Insert(6);
	BT->Left->Right->Left = Insert(5);
	BT->Right->Left = Insert(7);
	BT->Right->Right = Insert(9);
	BT->Right->Left->Right = Insert(8);

	cout << "先序递归遍历：";
	PreOrderTraversal_Recursion(BT);
	cout << "\n先序非递归遍历：";
	PreOrderTraversal(BT);

	cout << "\n中序递归遍历：";
	InOrderTraversal_Recursion(BT);
	cout << "\n中序非递归遍历：";
	InOrderTraversal(BT);

	cout << "\n后序递归遍历：";
	PostOrderTraversal_Recursion(BT);
	cout << "\n后序非递归遍历：";
	PostOrderTraversal(BT);

	cout << "\n层次遍历：";
	LevelOrderTraversal(BT);

	cout << "\n输出叶子结点：";
	FindLeaves(BT);

	cout << "\n输出树的高度：" << GetHeight(BT) << endl;

	system("pause");

	return 0;
}

代码运行结果如下图所示。

在这里插入图片描述