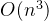【区间动态规划】P1775 石子合并（弱化版）

题目描述

设有 N(N≤300) 堆石子排成一排，其编号为 1,2,3,⋯,N。每堆石子有一定的质量 mi (mi≤1000)。现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同，合并的总代价也不相同。试找出一种合理的方法，使总的代价最小，并输出最小代价。

输入格式

第一行，一个整数 N。

第二行，N 个整数 mi。

输出格式

输出文件仅一个整数，也就是最小代价。

输入输出样例

输入 #1

4
2 5 3 1

输出 #1

一、题目分析

首先，这道题是不能用贪心的方法去解的。因为我们可以看到，题目只让合并相邻的两堆石子，如果是贪心的话，会让我们合并任意两堆石子。

二、题目做法

1.递归（超时）

我们考虑最后合并的两堆石子，那么我们可以找出一个分界线 x ，其中一堆是从第 1 堆石子到第 x 堆石子合并的结果，另外一堆是从第 x+1 堆到第 n 堆合并的结果。

那么当 x 确定的时候，总代价 = 从第 1 堆石子到第 x 堆石子合并的代价 + 从第 x+1 堆到第 n 堆合并的代价 + 总石子数。

现在我们并不知道 x 在哪里时总代价最小，所以我们可以枚举 x 。接下来，我们只需要递归就行了。假设我们要求合并第 l 堆到第 r 堆的最小代价，我们只需要枚举分界线 x 的位置，然后从 r-l 种方案中取代价最小的就行了。

注意，我们要加上总石子数，所以我们需要用到前缀和。

代码：

#include<bits/stdc++.h>
using namespace std;
int m[100010];
int s[100010];
int sol(int l,int r)
{
	if(l==r)
	{
		return 0;
	}
	int mn=1<<30;
	for(int i=l;i<r;i++)
	{
		mn=min(mn,sol(l,i)+sol(i+1,r));
	}
	return mn+s[r]-s[l-1];
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>m[i];
	}
	for(int i=1;i<=n;i++)
	{
		s[i]=s[i-1]+m[i];
	}
	cout<<sol(1,n);
	return 0;
}

2.记忆化

我们发现，使用递归的话，同一个区间 [ l , r ] 会被计算很多次，我们要怎么解决这个问题呢？

我们新开一个数组去记录合并第 l 堆到第 r 堆的最小代价，如果这个情况第一次出现，我们更新数组并继续递归，否则我们直接调用就行了。

代码：

#include<bits/stdc++.h>
using namespace std;
int m[100010];
int s[100010];
int f[510][510];
int sol(int l,int r)
{
	if(f[l][r]!=-1)
	{
		return f[l][r];
	}
	if(l==r)
	{
		return f[l][r]=0;
	}
	int mn=1<<30;
	for(int i=l;i<r;i++)
	{
		mn=min(mn,sol(l,i)+sol(i+1,r));
	}
	return f[l][r]=mn+s[r]-s[l-1];
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>m[i];
	}
	for(int i=1;i<=n;i++)
	{
		s[i]=s[i-1]+m[i];
	}
	memset(f,255,sizeof(f));
	cout<<sol(1,n);
	return 0;
}

3.DP求解

我们定义 f[i][j] 为合并第 i 堆到第 j 堆的最小花费。有了前面递归的思路，状态转移方程就很好列出啦：

f[i][j] = min ( f[i][j] , f[i][k] + f[k+1][j] + s[j] - s[i-1] )

而 f[1][n] ，合并第 1 堆到第 n 堆的最小花费，就是答案。

递归是自顶向下的思路，而递推是自底向上的思路。下面我们用两种方法进行 DP 。

①

我们第 1 个循环 j ，是枚举区间终点，第 2 个循环 i 是枚举区间起点，第 3 个循环 k 在区间内滑动。注意，我们的 i 应该从 j-1 处开始递减，从最小的区间 [ j - 1 , j ] 开始。 i 不能从 1 开始递增，否则就成了大区间到小区间了。

代码：

#include<bits/stdc++.h>
using namespace std;
int m[100010];
int s[100010];
int f[510][510];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>m[i];
	}
	for(int i=1;i<=n;i++)
	{
		s[i]=s[i-1]+m[i];
	}
	for(int i=1;i<=n;i++)
	{
		f[i][i]=0;
	}
	for(int j=2;j<=n;j++)
	{
		for(int i=j-1;i>=1;i--)
		{
			f[i][j]=1<<30;
			for(int k=i;k<j;k++)
			{
				f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
			}
		}
	}
	cout<<f[1][n];
	return 0;
}

②

另一种方法就是借助了一个变量 len ，它代表区间的长度。 len 从 2 开始遍历，从小区间到大区间枚举。而 i 的范围和 j 的范围就都由 len 算出来。

代码：

#include<bits/stdc++.h>
using namespace std;
int m[100010];
int s[100010];
int f[510][510];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>m[i];
	}
	for(int i=1;i<=n;i++)
	{
		s[i]=s[i-1]+m[i];
	}
	for(int i=1;i<=n;i++)
	{
		f[i][i]=0;
	}
	for(int len=2;len<=n;len++)
	{
		for(int i=1;i<=n-len+1;i++)
		{
			int j=len+i-1;
			f[i][j]=1<<30;
			for(int k=i;k<j;k++)
			{
				f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
			}
		}
	}
	cout<<f[1][n];
	return 0;
}

当然，这些代码的时间复杂度都是 $O(n^{3})$ ，后面我们会讲到其他的优化，不过这些代码已经可以通过本题了。