动态规划
引言
1951年,美国数学家贝尔曼(R.Bellman)等根据一类所谓多阶段决策问题的特性,提出了解决这类问题的“最优化原理”,并研究了许多实际问题,从而创立了最优化的一个新分支----动态规划。
动态规划没有统一的数学模型,对不同的问题要采用不同的方法去建立它们的模型。有了模型之后,要想得到数值解,仍然没有统一的处理方法。这是应当注意的。
1 动态规划原理
1.1 最短路问题及其解法
1.1.1 最短路问题及其特点
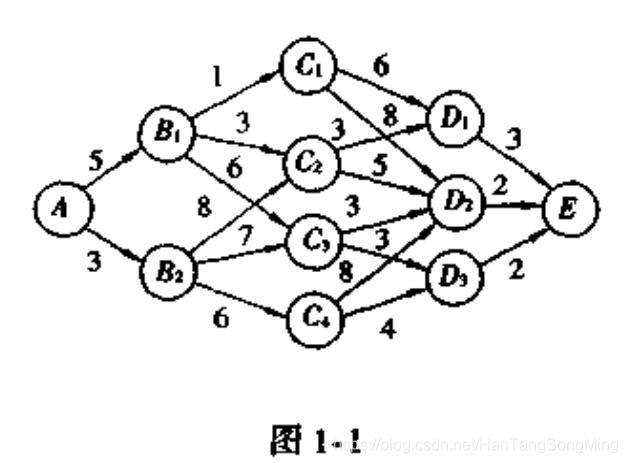
图1-1称为线路网络图,其中小圆圈称为点,两点间的连线称为弧,弧上的数字称为弧长。试求一条从起点 A A A到终点 E E E的连通弧,使其总弧长最短。称这类问题为最短路问题。
最短路问题的含义是广泛的,求解方法也有很多,下面介绍它的动态规划解法。
首先注意,从
A
A
A 到
E
E
E的整个过程可以分成从
A
A
A到B,从
B
B
B到
C
C
C,从
C
C
C到
D
D
D,再从
D
D
D到
E
E
E四个阶段。每个阶段都有起点,如第二个阶段有两个起点
B
1
B_1
B1 和
B
2
B_2
B2,用
x
k
x_k
xk表示第
k
k
k(
k
=
1
,
2
,
3
,
4
k = 1,2,3,4
k=1,2,3,4)个阶段的起点,并称它为状态变量。从每个起点出发都有若干个选择,例如从
B
1
B_1
B1出发有三种选择,到
C
1
C_1
C1或到
C
2
C_2
C2或到
C
3
C_3
C3,用
u
k
u_k
uk表示从第
k
k
k(
k
=
1
,
2
,
3
,
4
k = 1,2,3,4
k=1,2,3,4)个阶段的状态
x
k
x_k
xk出发所作的选择,并称它为决策变量。如果用
f
k
(
x
k
)
f_k(x_k)
fk(xk)1表示从第
k
k
k个阶段的状态
x
k
x_k
xk出发到终点
E
E
E的最短弧长,或者用
f
k
(
x
k
)
f_k(x_k)
fk(xk)2表示从起点
A
A
A到第
k
k
k个阶段的状态
x
k
x_k
xk的最短弧长,那么问题就变成求
f
1
(
x
1
)
=
f
1
(
A
)
f_1(x_1)=f_1(A)
f1(x1)=f1(A),或者求
f
5
(
x
5
)
=
f
5
(
E
)
f_5(x_5)=f_5(E)
f5(x5)=f5(E)。
其次,不难看出,如果最短路经过第
k
k
k阶段的状态为
x
k
x_k
xk,那么,从
x
k
x_k
xk出发到达终点
E
E
E的这条路线,对于从
x
k
x_k
xk出发到达终点
E
E
E的所有路线来说,显然也是最短路线。3
根据最短路问题的上述特点,可有下述两种解法。
1.1.2 逆序解法
用
f
k
(
x
k
)
f_k(x_k)
fk(xk)表示从第
k
k
k阶段的状态
x
k
x_k
xk出发到终点
E
E
E的最短弧长,从后向前逐步求出各点到达终点
E
E
E的最短路线的最短弧长,最后求出
f
1
(
x
1
)
=
f
1
(
A
)
f_1(x_1)=f_1(A)
f1(x1)=f1(A)即为所求最短路线的最短弧长。计算步骤如下:
(1)从最后一个阶段
k
=
4
k=4
k=4开始,按
f
4
f_4
f4的定义有
f
4
(
D
1
)
=
3
,
f
4
(
D
2
)
=
2
,
f
4
(
D
3
)
=
2
。
f_4(D_1)=3,f_4(D_2)=2,f_4(D_3)=2。
f4(D1)=3,f4(D2)=2,f4(D3)=2。
(2)当
k
=
3
k=3
k=3时,因为第3阶段有4个状态,而每个状态又有两个决策可选取,所以有
f
3
(
C
1
)
=
m
i
n
{
d
(
C
1
,
D
1
)
+
f
4
(
D
1
)
d
(
C
1
,
D
2
)
+
f
4
(
D
2
)
}
=
m
i
n
{
6
+
3
8
+
2
}
=
9
,
f_3(C_1)=min\left\{ \begin{array}{lcl} d(C_1,D_1)+f_4(D_1)\\ d(C_1,D_2)+f_4(D_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 6+3\\ 8+2 \end{array} \right\}=9,
f3(C1)=min{d(C1,D1)+f4(D1)d(C1,D2)+f4(D2)}=min{6+38+2}=9,
其中
d
(
⋅
,
⋅
)
d(\cdot,\cdot)
d(⋅,⋅)表示两点间的弧长。这说明从
C
1
C_1
C1到终点
E
E
E的最短弧长为9,路径为
C
1
→
D
1
→
E
C_1 \rightarrow D_1 \rightarrow E
C1→D1→E,决策为
u
3
(
C
1
)
=
D
1
u_3(C_1)=D_1
u3(C1)=D1。
f
3
(
C
2
)
=
m
i
n
{
d
(
C
2
,
D
1
)
+
f
4
(
D
1
)
d
(
C
2
,
D
2
)
+
f
4
(
D
2
)
}
=
m
i
n
{
3
+
3
5
+
2
}
=
6
,
f_3(C_2)=min\left\{ \begin{array}{lcl} d(C_2,D_1)+f_4(D_1)\\ d(C_2,D_2)+f_4(D_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 3+3\\ 5+2 \end{array} \right\}=6,
f3(C2)=min{d(C2,D1)+f4(D1)d(C2,D2)+f4(D2)}=min{3+35+2}=6,
即从
C
2
C_2
C2到终点
E
E
E的最短弧长为6,路径为
C
2
→
D
1
→
E
C_2 \rightarrow D_1 \rightarrow E
C2→D1→E,决策为
u
3
(
C
2
)
=
D
1
u_3(C_2)=D_1
u3(C2)=D1。
f
3
(
C
3
)
=
m
i
n
{
d
(
C
3
,
D
2
)
+
f
4
(
D
2
)
d
(
C
3
,
D
3
)
+
f
4
(
D
3
)
}
=
m
i
n
{
3
+
2
3
+
2
}
=
5
,
f_3(C_3)=min\left\{ \begin{array}{lcl} d(C_3,D_2)+f_4(D_2)\\ d(C_3,D_3)+f_4(D_3) \end{array} \right\} = min\left\{ \begin{array}{lcl} 3+2\\ 3+2 \end{array} \right\}=5,
f3(C3)=min{d(C3,D2)+f4(D2)d(C3,D3)+f4(D3)}=min{3+23+2}=5,
即从
C
3
C_3
C3到终点
E
E
E的最短弧长为5,路径为
C
3
→
D
2
(
或
D
3
)
→
E
C_3 \rightarrow D_2(或D_3) \rightarrow E
C3→D2(或D3)→E,决策为
u
3
(
C
3
)
=
D
2
(
或
D
3
)
u_3(C_3)=D_2(或D_3)
u3(C3)=D2(或D3)。
f
3
(
C
4
)
=
m
i
n
{
d
(
C
4
,
D
2
)
+
f
4
(
D
2
)
d
(
C
4
,
D
3
)
+
f
4
(
D
3
)
}
=
m
i
n
{
8
+
2
4
+
2
}
=
6
,
f_3(C_4)=min\left\{ \begin{array}{lcl} d(C_4,D_2)+f_4(D_2)\\ d(C_4,D_3)+f_4(D_3) \end{array} \right\} = min\left\{ \begin{array}{lcl} 8+2\\ 4+2 \end{array} \right\}=6,
f3(C4)=min{d(C4,D2)+f4(D2)d(C4,D3)+f4(D3)}=min{8+24+2}=6,
即从
C
4
C_4
C4到终点
E
E
E的最短弧长为6,路径为
C
4
→
D
3
→
E
C_4 \rightarrow D_3 \rightarrow E
C4→D3→E,决策为
u
3
(
C
4
)
=
D
3
u_3(C_4)=D_3
u3(C4)=D3。
(3)当
k
=
2
k=2
k=2时,由于第2阶段有2个状态,每个状态又有3个决策可选,故有
f
2
(
B
1
)
=
m
i
n
{
d
(
B
1
,
C
1
)
+
f
4
(
C
1
)
d
(
B
1
,
C
2
)
+
f
4
(
C
2
)
d
(
B
1
,
C
3
)
+
f
4
(
C
3
)
}
=
m
i
n
{
1
+
9
3
+
6
6
+
5
}
=
9
,
f_2(B_1)=min\left\{ \begin{array}{lcl} d(B_1,C_1)+f_4(C_1) \\ d(B_1,C_2)+f_4(C_2) \\ d(B_1,C_3)+f_4(C_3) \end{array} \right\} = min\left\{ \begin{array}{lcl} 1+9 \\ 3+6 \\ 6+5 \end{array} \right\}=9,
f2(B1)=min⎩⎨⎧d(B1,C1)+f4(C1)d(B1,C2)+f4(C2)d(B1,C3)+f4(C3)⎭⎬⎫=min⎩⎨⎧1+93+66+5⎭⎬⎫=9,
即从
B
1
B_1
B1到终点
E
E
E的最短弧长为9,路径为
B
1
→
C
2
→
D
1
→
E
B_1 \rightarrow C_2 \rightarrow D_1 \rightarrow E
B1→C2→D1→E,决策为
u
2
(
B
1
)
=
C
2
u_2(B_1)=C_2
u2(B1)=C2,
u
3
(
C
2
)
=
D
1
u_3(C_2)=D_1
u3(C2)=D1,
u
4
(
D
1
)
=
E
u_4(D_1)=E
u4(D1)=E。
f
2
(
B
2
)
=
m
i
n
{
d
(
B
2
,
C
2
)
+
f
4
(
C
2
)
d
(
B
2
,
C
3
)
+
f
4
(
C
3
)
d
(
B
2
,
C
4
)
+
f
4
(
C
4
)
}
=
m
i
n
{
8
+
6
7
+
5
6
+
6
}
=
12
,
f_2(B_2)=min\left\{ \begin{array}{lcl} d(B_2,C_2)+f_4(C_2) \\ d(B_2,C_3)+f_4(C_3) \\ d(B_2,C_4)+f_4(C_4) \end{array} \right\} = min\left\{ \begin{array}{lcl} 8+6 \\ 7+5 \\ 6+6 \end{array} \right\}=12,
f2(B2)=min⎩⎨⎧d(B2,C2)+f4(C2)d(B2,C3)+f4(C3)d(B2,C4)+f4(C4)⎭⎬⎫=min⎩⎨⎧8+67+56+6⎭⎬⎫=12,
即从
B
2
B_2
B2到终点
E
E
E的最短弧长为12,路径为
B
2
→
C
3
→
D
2
(
或
D
3
)
→
E
B_2 \rightarrow C_3 \rightarrow D_2(或D_3) \rightarrow E
B2→C3→D2(或D3)→E,或
B
2
→
C
4
→
D
3
→
E
B_2 \rightarrow C_4 \rightarrow D_3 \rightarrow E
B2→C4→D3→E,决策为
u
2
(
B
2
)
=
C
3
)
u_2(B_2)=C_3)
u2(B2)=C3),
u
3
(
C
3
)
=
D
2
(
或
D
3
)
u_3(C_3)=D_2(或D_3)
u3(C3)=D2(或D3),
u
4
(
D
2
)
=
E
u_4(D_2)=E
u4(D2)=E;或
u
2
(
B
2
)
=
C
4
u_2(B_2)=C_4
u2(B2)=C4,
u
3
(
C
4
)
=
D
3
u_3(C_4)=D_3
u3(C4)=D3,
u
4
(
D
3
)
=
E
u_4(D_3)=E
u4(D3)=E。
(4)当
k
=
1
k=1
k=1时,有
f
1
(
A
)
=
m
i
n
{
d
(
A
,
B
1
)
+
f
4
(
B
1
)
d
(
A
,
B
2
)
+
f
4
(
B
2
)
}
=
m
i
n
{
5
+
9
3
+
12
}
=
14
,
f_1(A)=min\left\{ \begin{array}{lcl} d(A,B_1)+f_4(B_1) \\ d(A,B_2)+f_4(B_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 5+9 \\ 3+12 \end{array} \right\}=14,
f1(A)=min{d(A,B1)+f4(B1)d(A,B2)+f4(B2)}=min{5+93+12}=14,
即从
A
A
A到终点
E
E
E的最短弧长为14,路径为
A
→
B
1
→
C
2
→
D
1
→
E
A \rightarrow B_1 \rightarrow C_2 \rightarrow D_1 \rightarrow E
A→B1→C2→D1→E,决策为
u
1
(
A
)
=
B
1
u_1(A)=B_1
u1(A)=B1,
u
2
(
B
1
)
=
C
2
u_2(B_1)=C_2
u2(B1)=C2,
u
3
(
C
2
)
=
D
1
u_3(C_2)=D_1
u3(C2)=D1,
u
4
(
D
1
)
=
E
u_4(D_1)=E
u4(D1)=E。
上述解法的四个步骤可归纳为下述递推公式:
{
f
k
(
x
k
)
=
min
u
k
∈
D
k
{
d
(
x
k
,
x
k
+
1
)
+
f
k
+
1
(
x
k
+
1
)
}
;
f
5
(
x
5
)
=
0
,
k
=
4
,
3
,
2
,
1
\left\{ \begin{array}{lcl} f_k(x_k) = \min \limits_{u_k \in D_k} \{ d(x_k,x_{k+1}) + f_{k+1}(x_{k+1})\} ;\\ f_5(x_5)=0, k=4,3,2,1 \end{array} \right.
{fk(xk)=uk∈Dkmin{d(xk,xk+1)+fk+1(xk+1)};f5(x5)=0,k=4,3,2,1
其中
x
k
+
1
=
u
k
(
x
k
)
x_{k+1}=u_k(x_k)
xk+1=uk(xk),即从状态
x
k
x_k
xk出发,采取决策
u
k
u_k
uk到达下一状态
x
k
+
1
x_{k+1}
xk+1;
D
k
D_k
Dk表示从状态
x
k
x_k
xk出发的所有可能选取的决策的集合;而
f
5
(
x
5
)
=
0
f_5(x_5)=0
f5(x5)=0称为边界条件,因为状态
x
5
=
E
x_5=E
x5=E已是终点。
这个递推公式就是最短路问题的数学模型,也叫动态规划方程。
由于这种算法的寻优方向与过程的行进方向刚好相反,故称逆序解法。
1.1.3 顺序解法
用
f
k
(
x
k
)
f_k(x_k)
fk(xk)表示从起点
A
A
A出发到第
k
k
k阶段的状态
x
k
x_k
xk的最短弧长,从前向后逐步求出起点
A
A
A到达各阶段起点的最短弧长,最后也可求出从起点
A
A
A到终点
E
E
E的最短弧长及其对应的路径。计算步骤如下:
按定义显然有
f
x
(
x
1
)
=
f
1
(
A
)
=
0
fx_(x_1)=f_1(A) = 0
fx(x1)=f1(A)=0,称它为边界条件。以下从第二阶段
k
=
2
k=2
k=2开始计算。
(1)当
k
=
2
k=2
k=2时,按
f
2
f_2
f2的定义有
f
2
(
B
1
)
=
5
,
f
2
(
B
2
)
=
3
。
f_2(B_1)=5,f_2(B_2)=3。
f2(B1)=5,f2(B2)=3。
(2)当
k
=
3
k=3
k=3时,按
f
3
f_3
f3的定义有
f
3
(
C
1
)
=
d
(
B
1
,
C
1
)
+
f
2
(
B
1
)
=
1
+
5
=
6
,
f_3(C_1)=d(B_1,C_1)+f_2(B_1)=1+5=6,
f3(C1)=d(B1,C1)+f2(B1)=1+5=6,
f 3 ( C 2 ) = m i n { d ( B 1 , C 2 ) + f 2 ( B 1 ) d ( B 2 , C 2 ) + f 2 ( B 2 ) } = m i n { 3 + 5 8 + 3 } = 8 , f_3(C_2)=min\left\{ \begin{array}{lcl} d(B_1,C_2)+f_2(B_1)\\ d(B_2,C_2)+f_2(B_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 3+5\\ 8+3 \end{array} \right\}=8, f3(C2)=min{d(B1,C2)+f2(B1)d(B2,C2)+f2(B2)}=min{3+58+3}=8,
f 3 ( C 3 ) = m i n { d ( B 1 , C 3 ) + f 4 ( B 1 ) d ( B 2 , C 3 ) + f 4 ( B 2 ) } = m i n { 6 + 5 7 + 3 } = 10 , f_3(C_3)=min\left\{ \begin{array}{lcl} d(B_1,C_3)+f_4(B_1)\\ d(B_2,C_3)+f_4(B_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 6+5\\ 7+3 \end{array} \right\}=10, f3(C3)=min{d(B1,C3)+f4(B1)d(B2,C3)+f4(B2)}=min{6+57+3}=10,
f 3 ( C 4 ) = d ( B 2 , C 4 ) + f 2 ( B 2 ) = 6 + 3 = 9. f_3(C_4)=d(B_2,C_4)+f_2(B_2)=6+3=9. f3(C4)=d(B2,C4)+f2(B2)=6+3=9.
(3)当
k
=
4
k=4
k=4时,按
f
4
f_4
f4的定义分别有
f
4
(
D
1
)
=
m
i
n
{
d
(
C
1
,
D
1
)
+
f
3
(
C
1
)
d
(
C
2
,
D
1
)
+
f
3
(
C
2
)
}
=
m
i
n
{
6
+
6
3
+
8
}
=
11
,
f_4(D_1)=min\left\{ \begin{array}{lcl} d(C_1,D_1)+f_3(C_1) \\ d(C_2,D_1)+f_3(C_2) \end{array} \right\} = min\left\{ \begin{array}{lcl} 6+6 \\ 3+8 \end{array} \right\}=11,
f4(D1)=min{d(C1,D1)+f3(C1)d(C2,D1)+f3(C2)}=min{6+63+8}=11,
f 4 ( D 2 ) = m i n { d ( C 1 , D 2 ) + f 3 ( C 1 ) d ( C 2 , D 2 ) + f 3 ( C 2 ) d ( C 3 , D 2 ) + f 3 ( C 3 ) d ( C 4 , D 2 ) + f 3 ( C 4 ) } = m i n { 8 + 6 5 + 8 3 + 10 8 + 9 } = 13 , f_4(D_2)=min\left\{ \begin{array}{lcl} d(C_1,D_2)+f_3(C_1) \\ d(C_2,D_2)+f_3(C_2) \\ d(C_3,D_2)+f_3(C_3) \\ d(C_4,D_2)+f_3(C_4) \end{array} \right\} = min\left\{ \begin{array}{lcl} 8+6 \\ 5+8 \\ 3+10 \\ 8+9 \end{array} \right\}=13, f4(D2)=min⎩⎪⎪⎨⎪⎪⎧d(C1,D2)+f3(C1)d(C2,D2)+f3(C2)d(C3,D2)+f3(C3)d(C4,D2)+f3(C4)⎭⎪⎪⎬⎪⎪⎫=min⎩⎪⎪⎨⎪⎪⎧8+65+83+108+9⎭⎪⎪⎬⎪⎪⎫=13,
f 4 ( D 3 ) = m i n { d ( C 3 , D 3 ) + f 3 ( C 3 d ( C 4 , D 3 ) + f 3 ( C 4 ) } = m i n { 3 + 10 4 + 9 } = 13 , f_4(D_3)=min\left\{ \begin{array}{lcl} d(C_3,D_3)+f_3(C_3 \\ d(C_4,D_3)+f_3(C_4) \end{array} \right\} = min\left\{ \begin{array}{lcl} 3+10 \\ 4+9 \end{array} \right\}=13, f4(D3)=min{d(C3,D3)+f3(C3d(C4,D3)+f3(C4)}=min{3+104+9}=13,
(4)当
k
=
5
k=5
k=5时,按
f
5
f_5
f5的定义有
f
5
(
E
)
=
m
i
n
{
d
(
D
1
,
E
)
+
f
4
(
D
1
)
d
(
D
2
,
E
)
+
f
4
(
D
2
)
d
(
D
3
,
E
)
+
f
4
(
D
3
)
}
=
m
i
n
{
3
+
11
2
+
13
2
+
13
}
=
14
,
f_5(E)=min\left\{ \begin{array}{lcl} d(D_1,E)+f_4(D_1) \\ d(D_2,E)+f_4(D_2) \\ d(D_3,E)+f_4(D_3) \end{array} \right\} = min\left\{ \begin{array}{lcl} 3+11 \\ 2+13 \\ 2+13 \end{array} \right\}=14,
f5(E)=min⎩⎨⎧d(D1,E)+f4(D1)d(D2,E)+f4(D2)d(D3,E)+f4(D3)⎭⎬⎫=min⎩⎨⎧3+112+132+13⎭⎬⎫=14,
f
5
(
E
)
=
14
f_5(E)=14
f5(E)=14为所求的最短弧长,路径为
A
→
B
1
→
C
2
→
D
1
→
E
A \rightarrow B_1 \rightarrow C_2 \rightarrow D_1 \rightarrow E
A→B1→C2→D1→E,决策为
u
1
(
A
)
=
B
1
u_1(A)=B_1
u1(A)=B1,
u
2
(
B
1
)
=
C
2
u_2(B_1)=C_2
u2(B1)=C2,
u
3
(
C
2
)
=
D
1
u_3(C_2)=D_1
u3(C2)=D1,
u
4
(
D
1
)
=
E
u_4(D_1)=E
u4(D1)=E,与逆序解法的结果完全一样。
上述解法也可写成统一的递推公式形式:
{
f
k
(
x
k
)
=
min
u
k
−
1
∈
D
k
−
1
{
d
(
u
k
−
1
,
x
k
)
+
f
k
−
1
(
x
k
−
1
)
}
;
f
1
(
x
1
)
=
0
,
k
=
2
,
3
,
4
,
5.
\left\{ \begin{array}{lcl} f_k(x_k) = \min \limits_{u_{k-1} \in D_{k-1}} \{ d(u_{k-1},x_k) + f_{k-1}(x_{k-1})\} ;\\ f_1(x_1)=0, k=2,3,4,5. \end{array} \right.
{fk(xk)=uk−1∈Dk−1min{d(uk−1,xk)+fk−1(xk−1)};f1(x1)=0,k=2,3,4,5.
其中
x
k
−
1
=
u
k
−
1
(
x
k
)
x_{k-1}=u_{k-1}(x_k)
xk−1=uk−1(xk),即从第
k
k
k阶段的起点状态
x
k
x_k
xk通过
u
k
−
1
u_{k-1}
uk−1去寻找第
k
−
1
k-1
k−1阶段的起点
x
k
−
1
x_{k-1}
xk−1,
f
1
(
x
1
)
=
0
f_1(x_1)=0
f1(x1)=0称为边界条件。
由于这种算法的寻优方向与过程的行进方向相同,故称顺序解法。