今天带领大家学一下哈夫曼
一. 概念:
赫夫曼树又叫做最优二叉树,它的特点是带权路径最短。
1)路径:路径是指从树中一个结点到另一个结点的分支所构成的路线,
2)路径长度:路径长度是指路径上的分支数目。
3)树的路径长度:树的路径长度是指从根到每个结点的路径长度之和。
4)带权路径长度:结点具有权值,从该节点到根之间的路径长度乘以结点的权值,就是该结点的带权路径长度。
5)树的带权路径长度(WPL):树的带权路径长度是指树中所有叶子结点的带权路径长度之和。
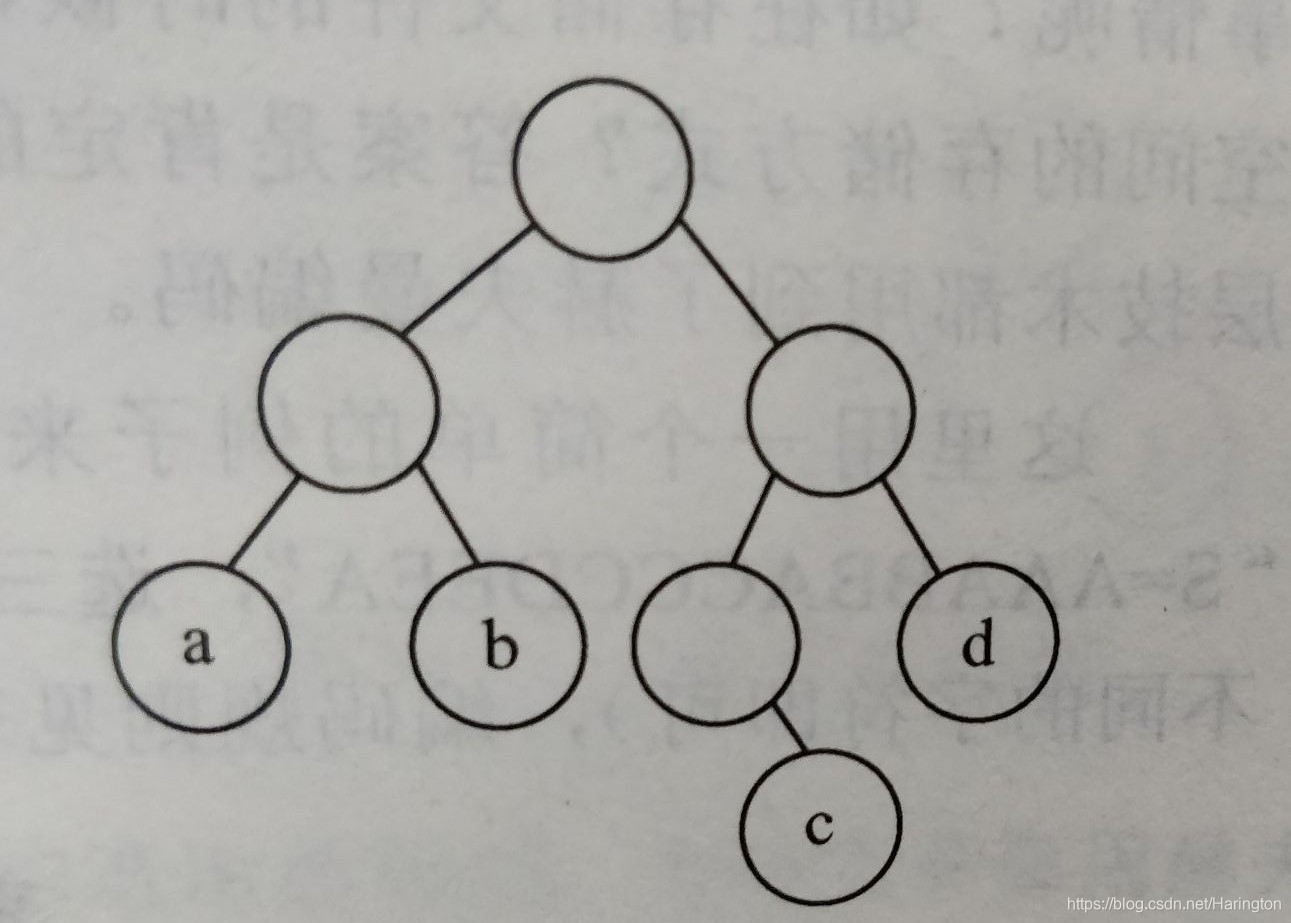
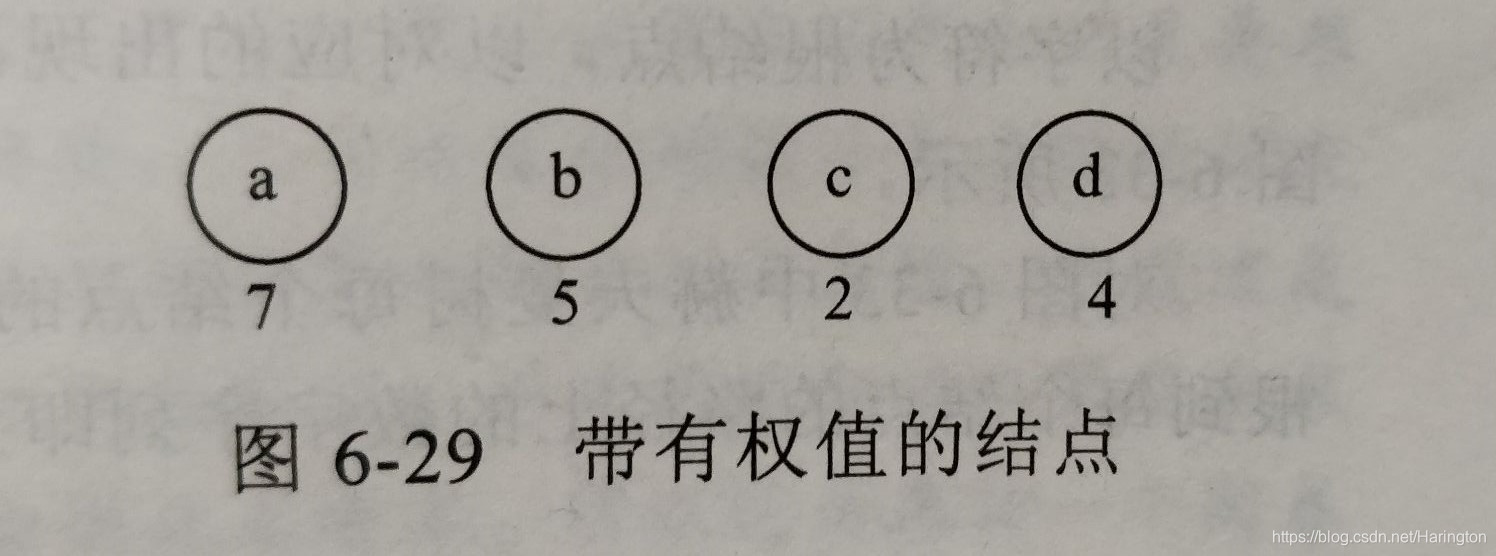
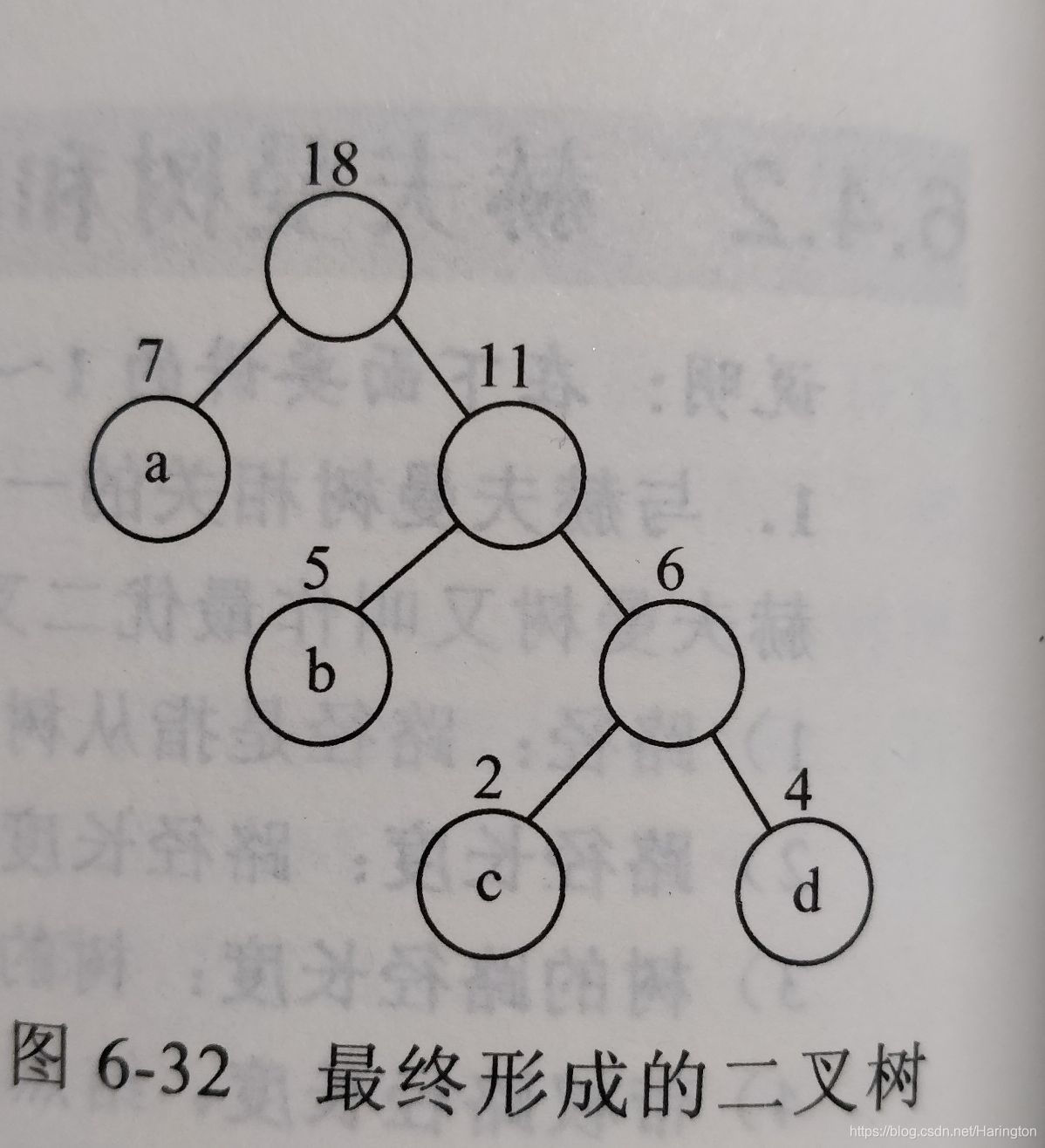
举个例子 a b c d 四个结点,权值分别为 7,5,2,4
如图所示二叉树的4个叶子结点。a根结点的分支数目为2,a的路径长度为2,a 的带权路径长度为 7*2 = 14
同样 b 的带权路径长度为 5 * 2 = 10。c , d 的分别是 3 * 2 = 6, 4 * 2 = 8。
这棵树的带权路径长度为 WPL = 8 + 6 + 10 + 14.
二. 赫夫曼树的构造方法
还是上面的例子把
a b c d 四个结点,权值分别为 7,5,2,4
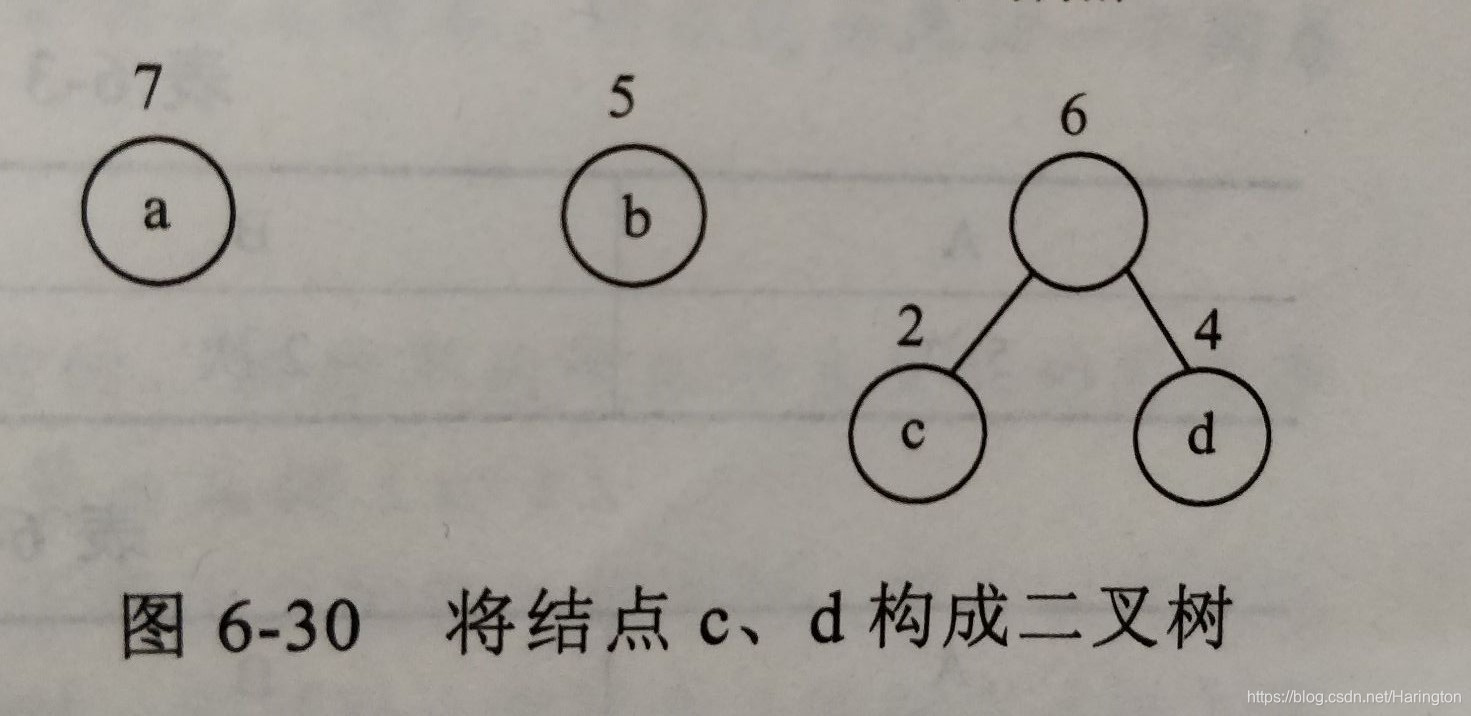
(1)我们选出权值最小的两个根c和d,作为左子树和右子数 构成一棵二叉树,新二叉树的根结点权值为c和d权值之和。删出c和d。同时将新构造的二叉树加入集合点。如下图
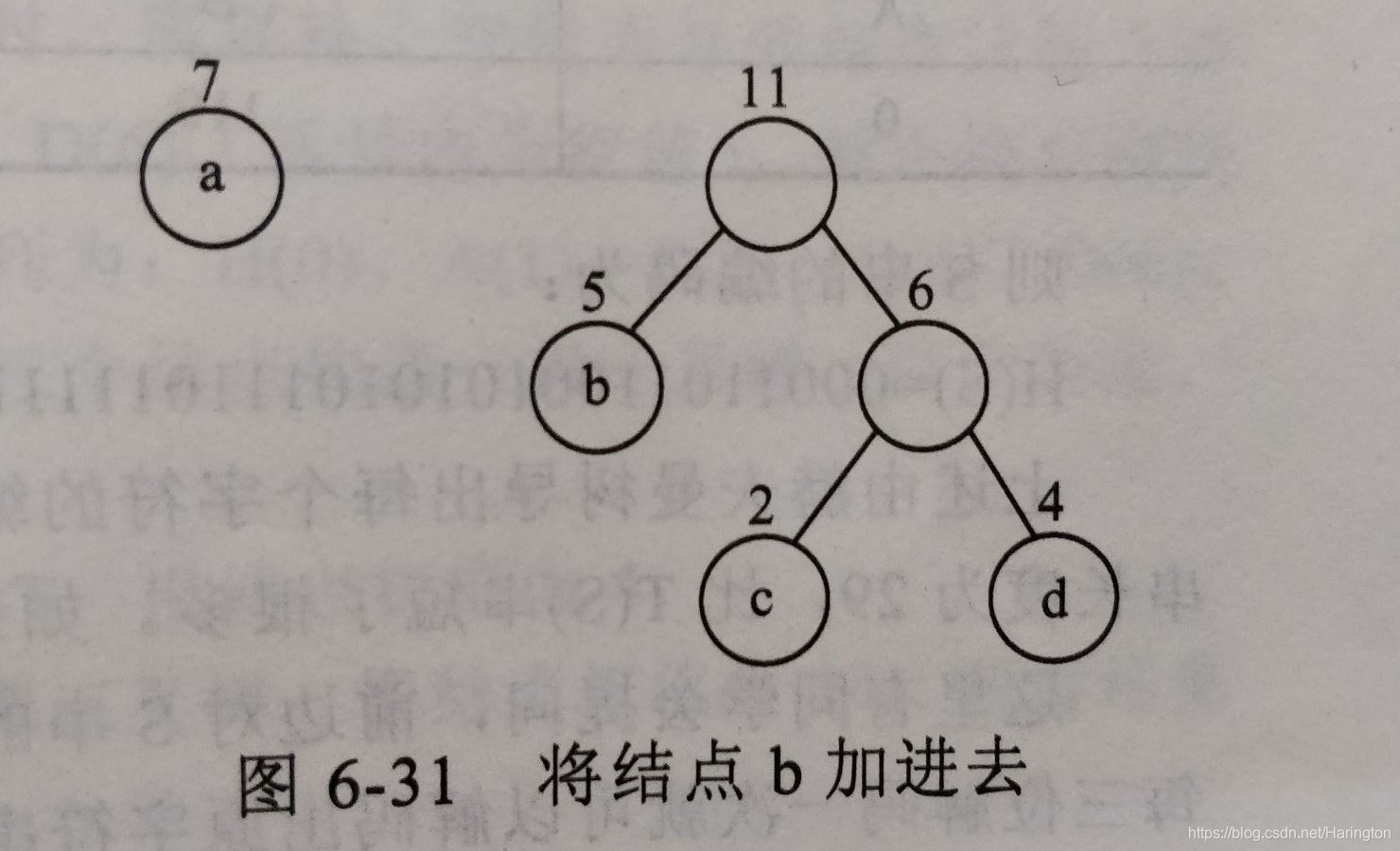
继续从 选择权值最小的两个根,即权值为 5和6 的两个结点,然后以它们作为左右子树构造一个新的二叉树。新的二叉树的权值为 5 + 6 = 11,删除 权值为 5和6 的两棵树,将新构造权值为11的树加如集合。
继续从选择权值最小的 直到所有集合中只剩下一棵二叉树。
此时集合中只剩下这一刻二叉树,这棵树就是赫夫曼树,至此赫夫曼树的构造结束,计算值为WPL = 7*1 + 5*2 + 2*3 + 4*3 = 35
在以a b c d这4个结点为叶子结点的所有二叉树中,赫夫曼树的WPL最小
赫夫曼树的特点
1)权值越大的结点,距离根节点越近。
2)树种没有度为 1 的结点,这类树有叫做 正则(严格)二叉树。
3)树的带权路径长度最短
4)赫夫曼树不唯一
三. 赫夫曼编码
前面关于赫夫曼树的讲解中 多次提到最,最优二叉 最短带权路径长度。所以说我们的赫夫曼树一定是有很大的作用的。比如在存储文件的时候,对于包含同一内容的文件有多种存储方式,是不是可以找出一种最节省空间的存储方式呢?答案是肯定的,不然我就不会问。这就是赫夫曼编码的用途,常见的zip压缩文件和.jpeg图片文件的底层技术都用到了赫夫曼编码。
现在给大家举一个简单的例子来说明赫夫曼编码如何实现对文件进行压缩储存的,如这样一串字符“S = AAABBACCCDEEA” 选用3位长度的二进制为各个字符编码(二进制数位随意,只要够编码所有不同的字符即可)
这是我们使用常规编码后,每个字符的编码号
根据该表我们可以把S串编码为:
T(S)= 000000000001001000010010010011100100000 该串长度为 39,那有没有办法使这个编码串的长度变小呢?并且能准确解码得到原来的字符串?下面我们用赫夫曼树试一试。
First step: 我们先统计各个字符出现的次数。
A 5次 ,B 2次 , C 3次,D 1次,E 2次
Second: 我们以字符为结点,以出现的次数为权值,构造赫夫曼树。
对应赫夫曼树的每个结点的左右分支进行编号,从根结点开始,向左为 0 向右为 1 。之后从根到每个结点路径上的数字序列即为每个字符的编码,
| A~E的赫夫曼编码为 | ||||
| A | B | C | D | E |
| 0 | 110 | 10 | 1110 | 1111 |
怎S串的编码为H(S) = 00011011001010101110111111110
上述由赫夫曼树导出每个字符的编码,进而得到对整个字符串的编码过程称为赫夫曼编码。H(S)的长度为29,必T(S)短了很多,前面每三位代表一个字符,解码时每三位解一次就可以得出源码,而现在赫夫曼解码确是不定长的,不同的字符可能出现不同的编码串,这样如果出现一个字符的编码串是另一个字符串编码的前缀,岂不是会出现解码的歧义?例如 A的编码是0 B的是00 那对于 00这个编码是 AA呢还是B呢?这个问题可以用前缀码来解决,即任何一个字符的编码都不是另一个字符编码的前缀。而赫夫曼编码产生的就是前缀码 ,因为被编码的字符都处与叶子结点上,而根通往任何一叶子结点的路径都不可能是通往其余叶子结点路径的子路径。因此任何一编码串的子串不可能是其他编码串的子串
其实 大家随便画一棵二叉数也能构造出前缀码,为什么非要用赫夫曼树呢?
由赫夫曼树的特性可知,其树的带权路径的长度最短。赫夫曼编码过程中,每个字符的权值是在字符串中出现的次数,出现的次数越多,距离根节点就越近,每个字符的编码长度就是这个字符的路径长度。因此得到的整个字符串的长度一定是最短的,结论赫夫曼编码产生的就是最短前缀码
四. 赫夫曼n叉树
赫夫曼可不止二叉树哦,
赫夫曼二叉树只是赫夫曼树的一种。
我们怎么去构造一个赫夫曼n叉树呢? 来举个栗子,
序列A B C D 权值分别为 1 3 4 6 怎么构造一个三叉树呢? 这时我们发现无法直接构造,我们需要补上权值为0的结点让整个序列可以凑成构造赫夫曼3插树的序列,E 的权值为 0, 然后类似二叉树的构建方法。每次挑权值最小的三个结点构造一棵三叉树,以此类推,直至集合中所有结点都加入树中。
重点:当发现无法构造时,(1),补权值为0的结点让整个序列可以凑成构造赫夫曼n插树的序列。(2)类似构造赫夫曼二叉树的方法构造n叉树,直至所有结点都加入树中
赫夫曼树的编码 代码 解码 建树过程
现在让我们一步一步构思
从最简单的开始,先给你 A B C D 4个节点 权值分别为 5 4 2 7
把他们一起存到一个数组内,然后 遍历 找到2个权值最小的 节点相加然后加入数组,标记一下,这两个及节点就被删除了,两个节点相加得到新的节点,加入到数组中,之后再继续 遍历 找到权值最小的两个点,继续重复上述操作,直到所有前面的 最初的 4 个节点都用过。(下面数组我们对第0列弃用,方便填下标)
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| weight | 0 | 5 | 4 | 2 | 7 | 0 | 0 | 0 |
| parent | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| lchild | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| rchild | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
我们进行第一次遍历 找到最小的两个数 4 2 然后让他们作为左右子树构造成一个 二叉树 将这个 新的权值 2+4 = 6填入到下标第一空的地方,将 2 和 4 的parent 改为 新建权值的下标 将 新建节点的左右子树 改为两个节点的 下标
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| weight | 0 | 5 | 4 | 2 | 7 | 6 | 0 | 0 |
| parent | 0 | 0 | 5 | 5 | 0 | 0 | 0 | 0 |
| lchild | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 |
| rchild | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 |
之后继续遍历 weight 从第1个 到 第5个 找到 权值最小的两个(2 和 4已经被用过了)找到 5 和 6,继续建树 。新建树的权值为 11 ,然后改 5 和 6 的parent 为 新建权值的下标 6.改新建权值的 lchild为 1 。rchild 为 5。
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| weight | 0 | 5 | 4 | 2 | 7 | 6 | 11 | 0 |
| parent | 0 | 6 | 5 | 5 | 0 | 6 | 0 | 0 |
| lchild | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 |
| rchild | 0 | 0 | 0 | 0 | 0 | 3 | 5 | 0 |
然后我们继续遍历找到 7 和 11 继续建树,加到数组的最后一个位置 改 7 和 11 的parent 改为 7, 新建节点18 的lchild 为 权值为7的下标4 .新建节点18 的 rchild 为权值为11 的下标6.这时所有的节点都用完了,我们构建赫夫曼树完成。
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| weight | 0 | 5 | 4 | 2 | 7 | 6 | 11 | 18 |
| parent | 0 | 6 | 5 | 5 | 7 | 6 | 7 | 0 |
| lchild | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 4 |
| rchild | 0 | 0 | 0 | 0 | 0 | 3 | 5 | 6 |
然后求 每个字符的Huffman编码。
我们从举个例子,先找第一个 字符的huffman编码,也就是权值为 5 的赫夫曼编码,
1)先构建一个栈。
2)然后找第一个字符的 parent,判断是lchild 还是 rchild。(parent 是 6)找到下标为6的列
3)判断是lchild 还是 rchild。如果是lchild 则向栈中 压入0,如果是rchild 则向栈中压入1.(左孩子,把0压入栈中)
4)然后继续找parent。(找到6(权值11)的parent,下标为 7),重复操作 (3)操作(4)直到 Parent 变为0结束(也就是根节点)。然后弹栈,用一个数组接收。
然后我们求出第一个字符的 赫夫曼编码是 10
下面给个题:
给定报文中26个字母a-z及空格的出现频率{64, 13, 22, 32, 103, 21, 15, 47, 57, 1, 5, 32, 20, 57, 63, 15, 1, 48, 51, 80, 23, 8, 18, 1, 16, 1, 168},构建哈夫曼树并为这27个字符编制哈夫曼编码,并输出。模拟发送端,从键盘输入字符串,以%为结束标记,在屏幕上输出输入串的编码;模拟接收端,从键盘上输入0-1哈夫曼编码串,翻译出对应的原文
#include<iostream>
#include<stdlib.h>
#include<stack>
#include<cstring>
#include<string.h>
using namespace std;
typedef struct
{
int weight;
int parent, lchild, rchild;
}HTNode, *HuffmanTree;
typedef char **HuffmanCode;
void Select(HuffmanTree &HT, int end, int &s1, int &s2) //找出最小的两个值。两个最小的值得下标记录到 s1 s2中。
{
int min1 = 0x3f3f3f, min2 = 0x3f3f3f;
for(int i = 1; i <= end; i++)
{
if(HT[i].parent == 0 && HT[i].weight < min1)
{
min1 = HT[i].weight;
s1 = i;
}
}
for(int i = 1; i <= end; i++)
{
if(HT[i].parent == 0 && HT[i].weight < min2 && s1 != i)
{
min2 = HT[i].weight;
s2 = i;
}
}
}
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n) //创建赫夫曼树和赫夫曼编码
{
int i, s1, s2;
HuffmanTree p;
if(n <= 1)
return ;
int m = 2 * n - 1;
HT = (HuffmanTree) malloc((m + 1) * sizeof(HTNode));
for(p = HT + 1, i = 1; i <= n; i++, p++, w++)
{
*p = {*w, 0, 0, 0};
}
for(; i <= m; i++, p++)
*p = {0, 0, 0, 0};
for(i = n + 1; i <= m; i++)
{
Select(HT, i-1, s1, s2);
HT[i].weight = HT[s1].weight + HT[s2].weight;
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
}
//从叶子到根逆向求每个字符的赫夫曼树编码
stack<char> s;
for(i = 1; i <= n; i++)
{
int temp = i, p, k = 0;
p = HT[temp].parent;
while(p)
{
if(HT[p].lchild == temp)
s.push('0');
if(HT[p].rchild == temp)
s.push('1');
temp = p;
p = HT[temp].parent;
k++;
}
int j = 0;
while(!s.empty())
{
HC[i][++j] = s.top();
s.pop();
}
HC[i][0] = j;
}
}
void showHuffmanCode(HuffmanCode HC) //显示每个字符的赫夫曼编码
{
char c ;
for(int i = 1; i <= 27; i++){
if(i != 27)
{
c = i + 'A' - 1;
cout << c << "的赫夫曼编码是:";
}
else
{
cout << "空格的赫夫曼编码是:";
}
for(int j = 1; j <= HC[i][0]; j++)
{
cout << HC[i][j];
}
cout << endl;
}
}
void TanserString(HuffmanCode HC,string s) //将字符转化为赫夫曼编码
{
string ss;
for(int i = 0; i < s.length(); i++)
{
if(s[i] >= 'A' && s[i] <= 'Z')
s[i] += 32;
if(s[i] == ' ')
s[i] = 'z' + 1;
}
for(int i = 0; i < s.length(); i++)
{
for(int j = 1; j <= HC[s[i] - 'a' + 1][0] ;j++)
ss += HC[s[i] - 'a' + 1][j];
}
cout << ss << endl;
}
void TanserHuffmanCode(HuffmanCode HC,string s) //将赫夫曼码变为字符
{
string ss = "", s1 = "";
string t[27];
for(int i = 0 ; i < 27 ;i++)
{
t[i] = "";
for(int k = 1; k <= HC[i + 1][0] ;k++)
{
t[i] += HC[i + 1][k];
}
}
for(int i = 0; i < s.size(); i++)
{
ss += s[i];
for(int j = 0; j < 27; j++)
{
if(ss == t[j])
{
ss = "";
if(j != 26)
{
s1 += j + 'a' ;
}
else if(j == 26)
{
s1 += ' ';
}
}
}
}
cout << s1 << endl;
}
void help(){
cout << "************************************************************" << endl;
cout << "******** 1.输入HuffmanTree的参数 ****" << endl;
cout << "******** 2.初始化HuffmanTree参数.《含有26字母及空格》 ****" << endl;
cout << "******** 3.创建HuffmanTree和编码表。 ****" << endl;
cout << "******** 4.输出编码表。 ****" << endl;
cout << "******** 5.输入编码,并翻译为字符。 ****" << endl;
cout << "******** 6.输入字符,并实现转码 ****" << endl;
cout << "******** 7.退出 ****" << endl;
cout << "************************************************************" << endl;
}
int main ()
{
HuffmanTree HT;
HuffmanCode HC;
string s;
HC = (HuffmanCode) malloc ((27+1) * sizeof(char *));
for(int i = 1; i <= 28 ;i++)
HC[i] = (char *)malloc((27+1) * sizeof(char));
help();
int a[27] = {64, 13, 22, 32, 103, 21, 15, 47, 57, 1, 5, 32, 20, 57, 63, 15, 1, 48, 51, 80, 23, 8, 18, 1, 16, 1, 168};
int operator_code;
while (1)
{
cout << "请输入操作 :" << endl;
cin >> operator_code;
if(operator_code == 1)
{
HuffmanCoding(HT, HC, a, 27);
cout << "创建成功,1,2,3已完成,无需输入2,3" << endl;
}
else if(operator_code == 4)
{
showHuffmanCode(HC);
}
else if(operator_code == 5)
{
getchar();
cout << "请输入HuffmanCode:";
getline(cin,s);
TanserHuffmanCode(HC,s);
}
else if(operator_code == 6)
{
getchar();
cout << "请输入字符:";
getline(cin,s);
TanserString(HC,s);
}
else if( operator_code == 7)
{
break;
}
else
{
cout << "输入违法请重新输入" << endl;
}
}
return 0;
}