一、随参信道对传输信号的影响

1. 瑞利衰落和频率弥散

我们每天在使用的手机都能够接受信号，但是一般我们日常生活中却很少看到基站，那么手机所接受到的信号是经过什么样的信道到达的呢？

基站发送的信号在经过地面或墙壁反射到达手机，可以发现这样信号的传输不是只有一条传输路径直接到达我们使用的手机上的，而是通过多条的传输路径到达手机，由于信号的传输距离不同、环境不同，每条路径的衰耗不一样、时延迟不一样，这就是随参信道的三个典型特点

1. 信号的传输衰耗随时间变化
2. 信号的传输时延是随时间变化
3. 多径传播

那么在这样的信道条件下，手机锁接收到的信号会有什么样的特点呢？我们来举一个简单的例子：

假设基站发送的是一个单频的余弦波 $s(t)=Acos(wt)$，该信号的包络是A，它的频谱只有在0处有值；而包络乘以$cos(wt)$就可以得到发送信号的频谱，如下图所示：

这样的信号经过n条路径到达了接收端，那么接收到的信号会是什么样子呢？

$r(t)=a_1(t)cos{w}_c[t-{\tau }_1(t)]+a_2(t)cos{w}_c[t-{\tau }_2(t)]....+a_n(t)cos{w}_c[t-{\tau }_n(t)]$

其中$a_i(t)$是第i条路径到达的接收信号的振幅（随时间变化的衰耗），${\tau }_i(t)$是第i条路径到达的信号的时延（随时间变化的的时延）

令$\Phi (t)=-w_c{\tau }_i(t)$，则$r(t)={\sum }_{I=1}^n{a}_i(t)cos[t+{\Phi }_i(t)]$

其波形如下所示：

所以我们接收到的信号就是窄带随机过程的一个样本函数，而这样的样本函数有什么特点呢？由于窄带随机过程的包络服从瑞利分布，我们继续考察该信号：

所以这样一个包络的一维概率密度函数服从瑞利分布，也称为瑞利衰落。

这个包络和相位与发送信号的包络和相位有什么变化呢？

• 发送信号的包络是0频率的，它的频谱在0处有一个冲击；而接收信号的包络是一个缓慢变化的随机过程，它的频率分量不是0，由于这个缓慢变化，导致信号的频谱在0频率附近发生了展宽

• 如果$\Phi (t)$是常数的话对时间求导是为0的，但是现在$\Phi (t)$是随时间变化的，求导不为0。由于我们对相位关于时间求导得到的是相位对角频率，现在$\frac{d[w_{c}t+\Phi (t)]}{dt}=w_c+\frac{d\Phi (t)}{dt}$所以该信号的角频率也是发生变化的，我们接收到信号的角频率只能说是近似为$f_c$，也发生了展宽

这种展宽就称为频率弥散，发送信号经过随参信道发生的变化称为多径效应，具体变化如下：

1. 从波形上来看，发生了瑞利衰落
2. 从频率上来看，发生了频率弥散

这就是随参信道对发送信号产生的俩个影响

2. 频率选择性衰落

（1）多径时延扩展

我们从多径传播引起的多径时延扩展入手：多径传播导致收到的信号被展宽，造成信号时间扩散的现象称为多径时延扩展。多径时延迟扩展对发送信号有什么影响呢？

以俩径信道模型为例：发送一个码元宽度为$T_s$道单极性不归零信号101。

1. 可以发现当多径时延较小时，即$\tau <<T_s$，此时第二径对第一径的码间干扰非常小，接收信号与发送信号区别不大，不会影响判决
2. 如果多径时延较大时，取$\tau =T_s$，此时第二径对第一径产生了严重的码间干扰，接收信号与发送信号区别非常大，引起了验证的误码，影响了通信系统的可靠性

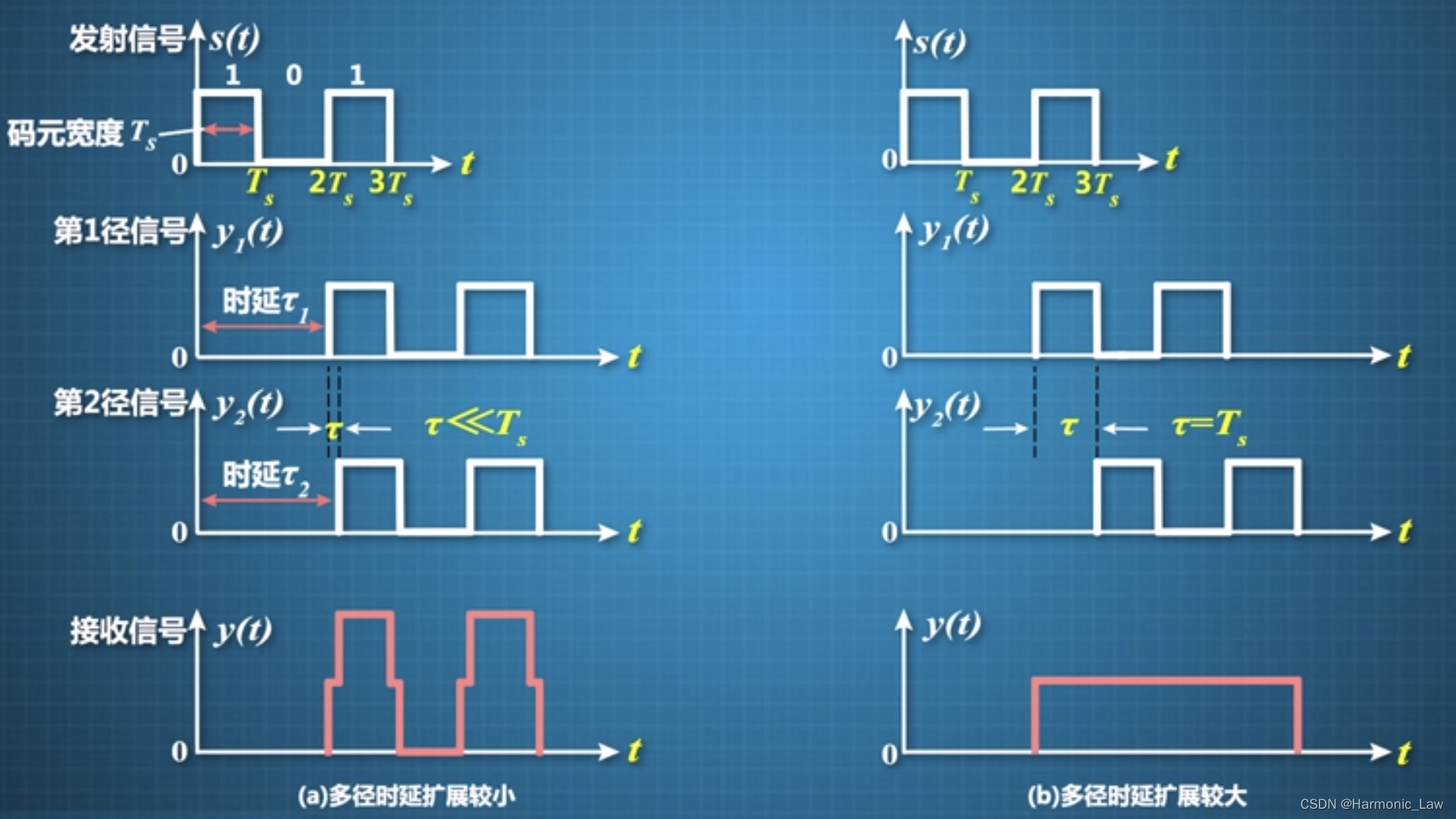
多径时延扩展在时域导致了码间干扰，那么在频域会导致什么呢？会导致频率选择性衰落

（2）频率选择性衰落

为什么呢？我们来从发送信号通过单径和俩径信道后信号的幅度谱的变化来寻找答案。

单径信道： 假设单径信道道衰减系数为1，传输时延为0，冲击响应$h(t)$自然就是 &(t)，其幅频特性如下所示

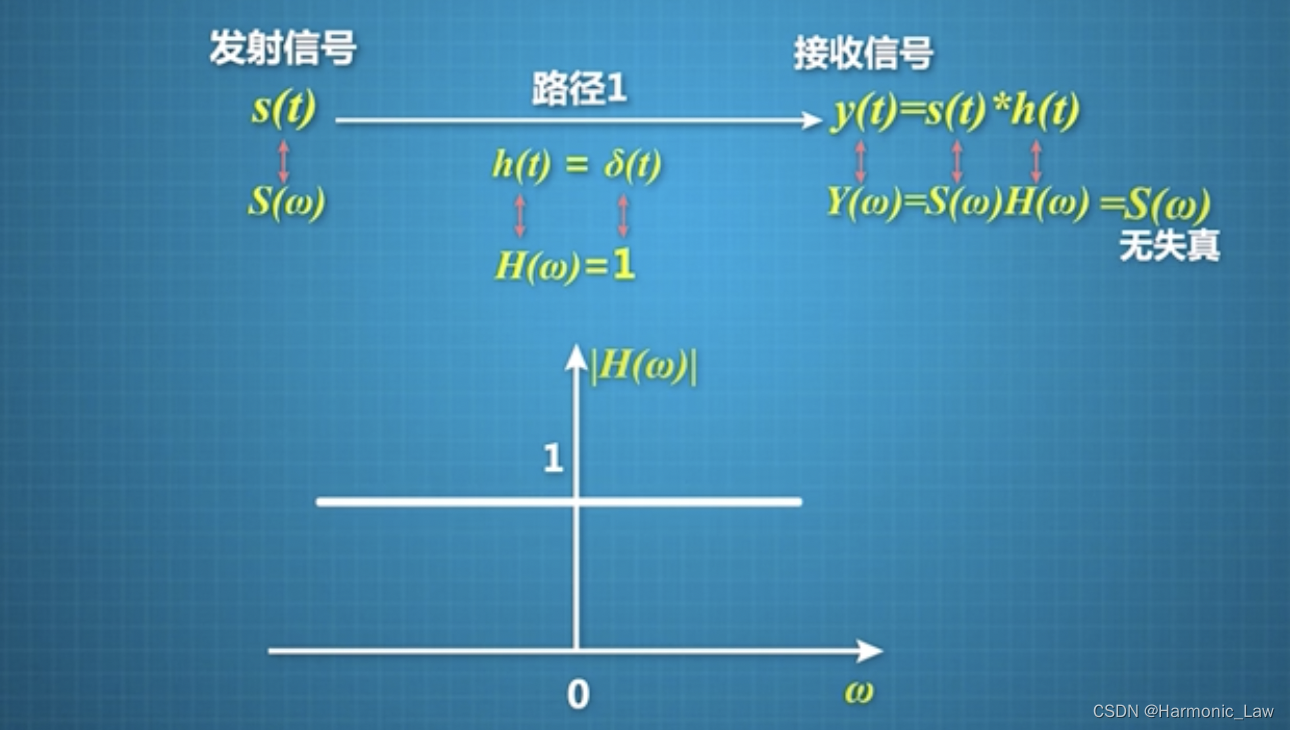
显然可以实现无失真传输

俩径信道： 在单径的基础上增加一条衰减系数为1，相对时延为$\tau$的路径，其冲击响应和幅频特性如下所示：

查看其传输函数$|H(w)|=2|cos(\frac{w\tau }{2})|$

可以发现俩个相邻谷底之间的频率间隔时$\frac{1}{\tau }$，

知道了单径和俩径信道道幅频特性后，我们来看发送信号经过单径和俩径信道后，幅度谱会发生什么变化？

假设发生信号$s(t)=\delta (t)$，经过信道后与查看接收信号的幅度谱

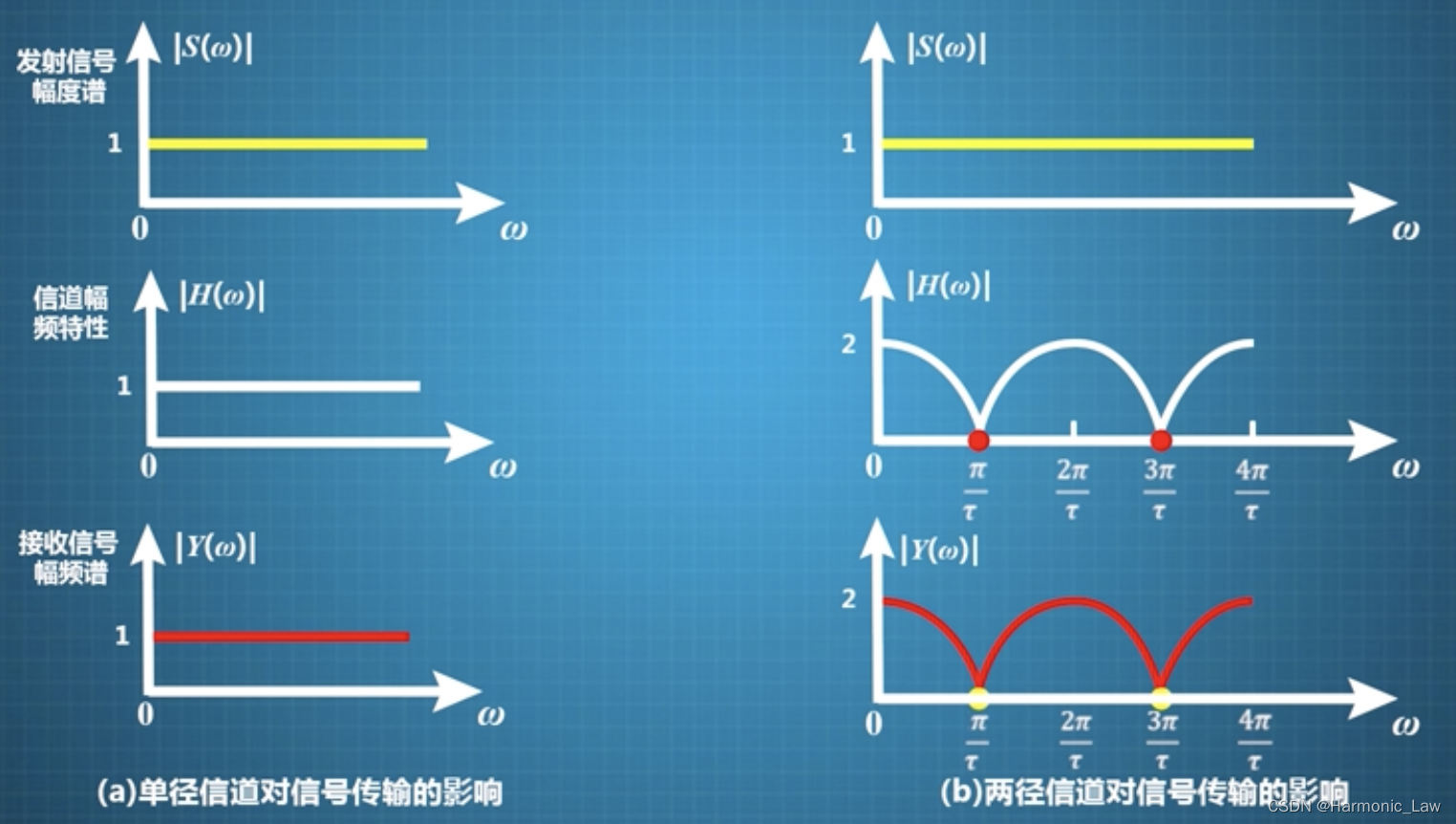
可以发现经过单径信道是信号没有失真，而经过俩径信道道时候，谷底对应的频率分量消失了，谷点附近的频率分量受到了严重的衰落，这就是频率选择性衰落。

• 单径信道由于没有相对时延差没有频率选择性衰落
• 俩径信道由于有相对时延差，其导致了频率选择性衰落

这就是对径时延扩展在频域导致频率选择性衰落的原因 ! ! !

现在我们来思考一下如何在时域中解释谷点处的频率分量为什么会消失?

假设发送信号时一个单频余弦信号，当俩条信道道时延$\tau$半个周期时，第一径和第二径在${\tau }_2$时刻道相位刚好相反，二者一叠加，接收到的信号就消失了，如下图：

此时信号的周期$T=2\tau$，频率为$\frac{1}{2\tau }$，刚好是谷点的位置。

同理：峰点位置对应信号的频率分量经过俩径信道后，同相相加，信号最强。

（3）相关带宽

那么如何判断信号经过俩径信道后是否发生了频率选择信衰落呢？ 这就需要比较信号带宽和相关带宽的大小了。

回到俩径信道的幅频特性，发现俩个相邻谷点之间的幅频特性比较接近，这意味着如果信号在俩个谷点之间的频率分量经过俩径信道后，接收信号的幅度时比较接近的，具有较强的相关性。而俩个相邻谷点之间的距离$\Delta f=\frac{1}{\tau }$就称为相关带宽

当信号带宽小于相关带宽时，不会发生频率选择性衰落，如下图所示：

那么如果信号带宽位于下图所示的位置，会不会发生频率选择性衰落呢？

易知发送信号是一个中心频率为$f_c$的窄带信号，由于峰点对信号的传输最有利，我们可以调整这个窄带信号中心频率的位置，使信号的频率分量避开谷点即可。

因此，只要信号带宽小于相关带宽，我们总有方法避免频率选择性衰落。

那么信号带宽的大小受什么影响呢？

• 由于 $\Delta f=\frac{1}{\tau }$，当时延$\tau \to \infty$时，$\Delta f\to 0$，多径时延迟扩展较大，在时域产生了严重的码间干扰
• 当时延$\tau \to 0$时，$\Delta f\to \infty$，相关带宽接近于单径时的情况，多径时延迟扩展较小，无码间干扰

而在实际的随参信道的特性远比俩径信道复杂，相对时延差通常使用最大时延差${\tau }_m$来表示，相关带宽 $\Delta f=\frac{1}{{\tau }_m}$。

实际工程中，为了避免频率选择性衰落要求信号带宽$B_s=(\frac{1}{5}\sim \frac{1}{3})\Delta f$

如果发生信号是全占空比的数字基带信号，由于$B_s=\frac{1}{T_s}$（是码元宽度的倒数），所以$T_s=(3\sim 5){\tau }_m$

（4）总结

二、连续信道的容量

1. 香农公式

白噪声背景下的连续信道容量为：$C=B{\log }_2(1+\frac{S}{N})$（b/s）

其等价为：$C=B{\log }_2(1+\frac{S}{n_{0}B})$（b/s）

• $S$：接收信号平均功率$(W)$；
• $B$：带宽 $(HZ)$
• $n_0$：噪声单边功率谱密度；
• $N=n_{0}B$：噪声功率

2. 如何有效提高连续信道容量

连续信道容量有三个要素：（1）带宽（2）接受信号功率（3）噪声的单边功率谱密度。

观察香农公式：$C=B{\log }_2(1+\frac{S}{N})$，我们可以想到如下提高信道容量的方式：

• 可以通过提高信号的发生功率，即增加基站的发射功率，也就增加了接收功率，提高了信道容量。我们可以在$S$较小时提高信号发送功率，但是如果信号功率已经比较大了，根据对数函数的性质，再提高信号发送功率增加的信道容量就非常小了；并且提高基站的发射功率会产生更大的电磁辐射，可能会对健康不利，因此这不是理想的方法。
• 可以提高信号的带宽，但是由于带宽是一种非常重要的资源，是由国家进行分配的，不能随意增加，因此这种方法不可行。但是即使能够增加信号带宽到无穷，信道容量也不可能无穷大，${\lim }_{B\to \infty }B{\log }_2(1+\frac{S}{n_{0}B})$近似等于$1.44\frac{S}{n_0}$
• 减少噪声功率，由于噪声单边功率谱密度是不受人为控制的，因此该方法不可行。

这三种方式似乎都不可行，我们转变思路

分集接收

从生活中的现象入手，在使用收音机的时候会出现信号质量不好的问题，这时候我们会想到将其换到另一个位置，信号质量也许就会变好，为什么呢？

这是因为在使用收音机的时候，接收到的信号可能会受到很多因素的影响，例如建筑物、地形、电磁干扰等。这些因素会造成信号衰减、信号遮挡、信号多径等问题，从而导致信号弱化，噪声增加，信号质量变差。

将收音机换到其他位置可能会改善信号质量，这是因为不同的位置有不同的信号传播环境。例如，在楼房顶上或野外空旷地区，没有建筑物和障碍物的干扰，信号容易穿透并传播得更远，因此信号质量可能会更好。而在室内或山谷等地方，由于存在各种障碍物，信号传播相对受限制，因此信号质量较差。这能给我们什么启发呢？

我们可以给收音机增加多根天线，这些天线在不同的位置，那么总会有一根天线的信号接收质量最好，但是如果只利用这一根天线的话其他接收天线就被浪费了，所以我们可以利用某些技术将其他天线接收到的信号进行合并，可以提高接收信号的有效性。这种利用多根接收机来同时接受同一个信号的技术称为分集接收

1. 分集接收是利用多个接收机同时接收同一信号的技术。这种技术通常应用于要求高可靠性、高抗干扰性的通信系统中，如航空、军事等领域。通过分集接收技术可以实现对信号的多路冗余处理，减小信号受干扰或衰减的影响，提高系统的可靠性和抗干扰能力。
2. 分集接收技术主要包括两类：空间分集和时域分集。空间分集是利用多个天线在空间中接收同一信号，并将它们进行合并来改善信号质量。时域分集则是利用一个接收机划分成多个子接收机，在时间上对信号进行冗余处理。
3. 在空间分集中，多个天线接收到的信号之间可能存在差异，这一差异可以被视为多路独立的输入信号。通过合理地对这些信号进行加权、合并等处理，可以消除干扰、抵抗衰落等影响，从而提高接收信号的可靠性。
4. 时域分集则是通过将接收到的信号分成多个时隙，在不同的时刻对信号进行处理。由于信号可能会在不同的时段受到不同的影响，因此在多个时隙上采集信号并将它们进行处理可以减小信号质量的波动，提高系统的可靠性。

此外，收音机的天线是一个非常重要的组成部分，不同类型、不同长度的天线也会对信号接收产生影响。因此，可以通过更换天线或者调整其方向来改善信号质量。

无论是发送端一根天线接收端多根天线，函数发送端多根天线接收端一根天线，他们都是可以达成同样的效果的。

但是要注意，使用多根天线来接收信号时不需要增加发送信号的功率，只需要增加接收端端天线，即增加了硬件成本。而在发送端使用多根天线来发送信号就需要增大发送信号的功率，并且在发送端增加了硬件成本。

通过上文的讨论，我们可以知道这种方式可以提高信号的可靠性和抗干扰能力，但是这种分集接收的方式有没有增加信道容量呢？答案是并没有

因为它只能通过提高信道的可靠性和抗干扰能力来降低误码率，从而提高通信系统的成功率和数据传输质量。换句话说，分集接收技术并没有改变信道的基本特性，即它的容量仍然受到信噪比、信道带宽等因素的限制。

看来这俩种通信方式不仅没有增加信道容量，还增加了信号的发送功率或者是硬件成本，只是增加了信号的可靠性和抗干扰能力，还是没有达成我们增大信道容量的目标，我们继续思考

如果我们将上述的俩种情况合并起来，就会出现多个发送天线和多根接收天线的情况，而这种多输入多输出的技术被称为MIMO技术，这能达到什么样的效果呢？这种方式能够增加信道容量吗？

我们先理解单输出多输入多情况，我们可以将接收端接收信号最好的一根天线拿出来，就等效为了单径传输的情况，所以它的信道容量没有增加。

现在来思考下图中abc信道容量的大小关系(假设带宽，信号发送功率和输出信噪比相同)

b图的信道容量是a图的俩倍，c图的信道容量是a图的三倍，那么d图呢？我们可以将其拆分：

可以看到它相当于俩个单径信道，所以信道容量是单径情况下的俩倍

所以对于MIMO系统的信道容量还和发送天线和接收天线的最小值有关，即$C=MB{\log }_2(1+\frac{S}{N})$，其中$M=min(发送天线数，接收天线数)$，这就提高了信道容量。

但是我们还是有些疑问：我们使用多个天线发送信号的总功率通常是比使用单个天线发送信号所需的功率要大的，因为在MIMO系统中，多个天线同时传输信号，因此需要更大的功率来支持这些信号的传输。那这样岂不是和我们最开始想到的第一种增加发送信号功率的方式一样了？我们还需要这种方式做什么？

现在我们假设发送端每一根天线发送所需的功率与发送端只有一根天线时发送相同信号所需功率相同（实际上前者低于后者)，即天线发送信号所需的功率不变。

• 如果我们使用第一种方式单纯增加信号的发送功率，增加到$10S$，那么更加香农公式可知信道容量并不会增加到原本的10倍，即$C^{\prime }<10C$，这是由指数函数的性质决定的。
• 但是如果我们使用MIMO系统，假设发送端有10根天线，接收端天线大于10根，当将发送端端总功率增加到10倍，近似相当于每一根天线发送端功率不变，仍为$S$，但是根据MINO系统下的香农公式，其信道容量增加了约10倍，可认为$C^{\prime }=10C$。

我们分析发现实际上增加相同的发送功率后者的方法增加的信道容量是大于前者的方法，并且在信号功率非常大的情况下，后者的信道容量将远大于前者，这就是使用使用MIMO系统。

使用多个天线发送信号时，每一个天线所需要的功率通常比使用单个天线发送信号所需的功率要小。这是由于在MIMO系统中，多个天线同时传输信号，每个天线仅需传输其中一部分的数据，从而使得每个天线所需的功率可以更低。此外，在MIMO系统中，可以针对某些信道进行波束成形的优化，使得信号能够更加集中地传输到指定位置，因此每个天线所需的功率还可以相对较小。

3. 香农公式的工程应用----扩频通信

在香农公式中，如果我们已经知道了信道的极限传输速率C，乘以一个时间T，结果就是时间T内传输的总信息量。那么香农公式就变成了$CT=BT{\log }_2(1+\frac{S}{N})$，此时传输称总信息量就和信号带宽$B$，传输时间$T$，以及信噪比$\frac{S}{B}$有关。

观察公式可以发现公式中的$B，T，{\log }_2(1+\frac{S}{N})$的地位是相等的，可以看作是矩形的三边，在保证总信号量$CT$不变的情况下，可以互换以上三者，这种互换就导致了一系列工程应用：

现在我们假设信号传输环境比较差，信噪比比较低，存在许多干扰，在时间T内接收端很难保证可以在规定时间内将信号完全接收到，为了保证总体信息量的不变，这时我们选择增加带宽，这种方式称为扩频通信，可以有效抵抗噪声干扰。

有的同学会有疑问：为什么明明带宽资源非常珍贵，还要使用这种增加带宽的方式来进行通信呢？是不是因为没有其他方法才取此下策？

先简单说明一下，后续做详细解释：这是因为我们之前所讨论的信道都是一个用户通信使用一个信道，如果仅仅为一个用户增加带宽就不太划算了；但是扩频通信可以通过采用多址技术，支持多个用户同时使用同一个信道！无需进行频率规划！并且不会产生互相干扰！这样为多个用户使用同一个较大带宽，比起每一个用户都使用不同的带宽的总带宽要更小一点，这样是不是就非常划算了!

那么如何进行扩频呢？我们来看下图：

假设我们所发送的的信号是一个简单的0～1序列，要想扩大其频率，我们可以利用一个称为扩频码的伪随机序列，该扩频码的码元周期远小于发送信号码元周期，将伪随机序列与发送信号相乘(异或)得到扩频信号。明显扩频信号的频域进行扩展。

在扩频通信中，信号变得宽广是通过使用扩散码进行调制实现的。这种调制方法可以将原始信号的频谱分散到非常宽的频带范围内，从而使得每个小部分的信号强度非常低。当噪声出现时，由于噪声也分布在整个频带内，因此会对每个小部分的信号产生一定程度的干扰和衰减，但总体而言不会对整个信号产生重大影响。

在接收端，接收到的信号需要采用相同的扩散码进行解调。由于扩散码是具有良好随机性的，与原始信号没有任何相关性，因此能够很好地抵抗噪声的干扰。即使某一部分的信号受到严重干扰或噪声，其他部分仍然能够被解调恢复出来。这就保证了信号的完整性，并且使扩频通信系统具有较好的抗干扰性能。

因此，通过扩散码的调制和解调过程，我们可以将信号在传输过程中变得非常宽广，这样即使出现一定程度的噪声和干扰，我们仍然能够保持信号的完整性，从而实现可靠的通信。

解频的方式如下图所示：

当接收端收到信号后，将收到的信号即扩频信号再次乘以扩频码，相当于进行异或，就得到了原始的发送信号

而这样的通信方式为什么可以抵抗噪声干扰？为什么可以让多个用户同时使用同一信道而不会产生明显干扰呢？这俩个问题将会一并得到解答

我们首先来看扩频信号的频谱特性和对窄带噪声的抑制作用：

发送信号在频域中是一个频率有限的带通信号，首先对其进行扩频操作，要注意扩频码的幅度是$+1$或$-1$，所以经过扩频后发送信号的功率是不变的(频域面积不变)，扩频信号的幅度较小，带宽较大；然后传入通信信道，进入信道后的扩频信号会遇到窄带干扰信号；接收端就会接收到扩频信号+窄带干扰信号的混合信号，接收端如何将混合信号中的原信号恢复出来呢？我们将接收到的混合信号乘以扩频码，那么原始发送信号就被恢复了，那干扰信号呢？干扰信号由于遭到了扩频，所以干扰信号幅度变小，带宽变宽，也就是本来很强的窄带干扰就变成了一个幅度低，带宽宽的干扰了，接收端可以通过带通滤波器来获取发送信号！

上述中我举的例子是一个窄带强干扰信号，如果干扰信号是一个幅度较大，带宽也较大的干扰信号时也可以使用上述方法来消除干扰吗？答案是可以的，但是有一点需要注意：我们使用的扩频码的带宽必须远大于噪声带宽，这样才能在第二次乘以扩频码时将噪声扩频，将噪声幅度变小，带宽变宽。

那么如何扩频通信是如何让多用户可以使用同一个信道呢？

也许有些同学已经明白原因了，对于一个用户而言，只需要将其他用户在信道中的扩频信号当作噪声处理就好了呀！

由于每一个用户都有自己的扩频码，我们只需要要求每一个用户的扩频码的带宽都非常大，这样所有在信道中的扩频信号，除了一个信号会被自己的扩频码恢复，在信道中的所有其他信号都将被扩频，然后通过带通滤波器就得到了唯一的一个信号。

如果你听懂了上述内容，那你一定可以明白下面这张图是在干什么，即使它并不清晰：

1. 信噪比换带宽----多进制多点平多星座图
2. 时间换信噪比----深空通信