一、基本概念

1. 模拟调制和数字调制

调制是指将信号（例如声音、图像、数据）转换成能够在信道中传输的信号形式的过程。在通信中，信息信号往往无法直接在信道中传输。因此，需要通过调制将信号转换成可以在信道中传输的模拟或数字信号。这个过程就像是将信息信号“嵌入”到另一个信号中一样。

调制的作用和目的：

• 把基带信号的频谱搬移到较高的频率处，就可以提高发送效率
• 把多个不同的基带信号搬移到不同的载频处，以实现信道的多路复用，提高信道利用率
• 扩展信号带宽，提高系统抗干扰能力

调制分为模拟调制和数字调制

• 模拟调制：将模拟信息信号（如声音、图像）通过一定的调制方式加到载波信号中，形成调制信号，然后将调制信号送入信道进行传输。在接收端，通过解调将调制信号中的信息信号提取出来。常见的模拟调制方式包括：调幅（AM）、调频（FM） 、调相（PM） 等。
• 数字调制：数字调制是将数字信息信号（如二进制数据）通过一定的调制方式转换成一组数字信号，形成数字调制信号，然后将数字调制信号送入信道进行传输。在接收端，通过解调将数字调制信号中的数字信息信号还原出来。常见的数字调制方式包括：脉冲编码调制（PCM）、正交振幅调制（QAM）、相移键控调制（PSK）、频移键控调制（FSK）等。

2. 基带调制和载波调制

调制又分为基带调制和带通调制/载波调制

• 基带调制：将原始信号直接调制成一个低频信号，然后再进行传输。这种调制方式不需要使用载波信号，因此信号的频率范围较低，通常占据的带宽比较窄。常见的基带调制方式有脉冲调制、脉冲编码调制等。
• 带通调制/载波调制：将原始信号调制到一个较高的载波频率上，然后进行传输。这种调制方式需要载波信号的支持，因此信号的频率范围比较广，在发送和接收端需要进行频率和相位同步以确保信号的正确解调。常见的带通调制方式有调幅、调频、调相等模拟调制和正交振幅调制、相移键控调制、频移键控调制等数字调制方式。

本文中只讨论载波调制的模拟调制系统

载波调制 就是利用调制信号去控制载波信号的某些参赛(例如幅度、频率、相位等)，使得载波的某些参数能够按照调制信号的规律变化。这种变化在信号传输过程中体现为信号频率、振幅、相位等的变化。如如调幅调制(AM)中，调制信号控制载波的幅度，调频调制(FM)中，调制信号控制载波的频率等等。

3. 载波调制解调的一般过程

载波调制是一种基于调制信号和载波信号相互作用的信号传输技术，过程如下：

• 基带/调制信号的产生：
• • 调制信号就是来自信源的基带信号，这个信号通常是低频信号，频率在几百赫兹或几千赫兹左右。该信号有某些关键的参数信息，该信号可以通过调制信号控制载波信号的某个或某些特征，使载波信号具有有调制信号相同的信息。
• 载波信号的产生：
• • 接下来，我们要产生一个高频信号，称为载波信号。载波信号可以是一个正弦波，频率通常在几兆赫兹（MHz）或更高。这个信号是一个没有任何信息的信号，只是作为一个容器用于传输基带信号。
• 调制过程：
• • 调制是将调制信号与载波信号相互作用的过程，以便将调制信号转换成可传输的信号，通常将调制信号调制到高频信号中的某一特定变量（如幅度、频率或相位）上，形成已调信号。根据调制方式不同，有调幅（AM)调制，调频（FM)调制等
• • 在调制过程中，调制信号的振幅、频率或相位决定了载波信号的振幅、频率或相位的改变，从而把原始信号的信息嵌入到了载波信号中。这样，我们就可以将基带信号通过载波信号进行传输。
• 解调过程：
• • 接收端接收到信号后，需要先将载波分离出来，然后再将携带信息的信号解出来。这个过程就称为解调。解调的过程与调制的过程相反，是将载波信号与解调信号相乘，从而得到带有信息的信号。最终，我们可以通过将解调后的信号进行放大、重构、编码等处理，使得前面的原始信号完整地呈现在接收端。
• • 在不同的载波调制方式中，具体的调制过程以及调制信号与载波信号之间的关系有所不同。例如，调幅调制（AM）中，调制信号控制载波信号的振幅；调频调制（FM）中，调制信号控制载波信号的频率；相位调制（PM）中，调制信号控制载波信号的相位。不同的调制方式在应用中具有不同的特点和适用场景。

二、AM调制解调原理及抗噪声性能分析

1. AM调制

标准调幅就是常规双边带调制，简称调幅(AM)。假设调制信号 $m(t)$ 的均值为0，将调制信号与一直流偏量 $A_0$ 叠加，然后与载波相乘，就得到了调幅信号 $s_m(t)$，调幅信号 $s_m(t)$ 在信道中传输的时候与噪声 $n(t)$ 叠加，接收端得到 $n(t)+s_m(t)$，此时将该信号通过带通滤波器，将噪声的频率分量限制在一定范围内，高斯白噪声$n(t)$变为窄带高斯噪声$n_i(t)$，然后得到接收端的输入信号 $s_i(t)$ 和接收端的输入噪声 $n_i(t)$

1. 时域

将调制信号与一直流偏量$A_0$叠加，然后与载波相乘，就得到了调幅信号$s_m(t)$ $$\begin{array}{r}{s}_m(t)=[A_0+m(t)]\cos {\omega }_{c}t\end{array}$$假设带通滤波器的传输函数为1，那么就有$s_i(t)=s_m(t)$

2. 频域
$$\begin{array}{r}F[A+m(t)]=2\pi A\delta (w)+M(w)\end{array}$$$$\begin{array}{r}{S}_m(w)=\pi A_0[\delta (w+w_c)+\delta (w-w_c)]+\frac{1}{2}[M(w+w_c)+M(w-w_c)]\end{array}$$假设带通滤波器的传输函数为$1$，那么就有$S_i(w)=S_m(w)$

3. 带宽

假设调制信号$s_m(t)$的带宽为$f_H$，由图像可知AM传输带宽是调制信号带宽的俩倍，即$B=2f_H$

4. 功率

• 输入信号功率

调制信号的平均功率为${\bar{P}}_m={\bar{m}}^2(t)$，直流分量的平均功率$P=A^2$，二者叠加后乘以载波$cos{w}_{c}t$，由于$\frac{1}{T}{\int }_{-T/2}^{T/2}cos{w}_{c}tdt=\frac{1}{2}$，所以可以得到任意信号与余弦信号相乘时功率减半，此时是调幅信号的功率如下：
$$\begin{array}{r}{P}_{AM}={\bar{s}}_m^2(t)=\frac{1}{2}[A^2+{\bar{m}}^2(t)]=P_c+\frac{1}{2}{P}_m=P_c+P_s\end{array}$$对于调幅信号来说，经过带通滤波器后信号功率不变，即$S_i=P_{AM}=P_c+P_s$

其中$P_c$是直流分量与载波相乘后的功率，称为载频功率，$P_s$称为边带功率；

只有边带功率才与调制信号有关，也就是说载波分量不携带信息，那么有用的功率占信号总功率的比可以写为：$$\begin{array}{r}{\mu }_{AM}=\frac{P_s}{P_{AM}}=\frac{{\bar{m}}^2(t)}{A_0^2+{\bar{m}}^2(t)}\end{array}$$我们把${\mu }_{AM}$称为调制效率，

在调制信号为单音余弦信号$m(t)=A_{m}cos{w}_{m}t$时，并且满调幅($|m(t){|}_{max}=A_0$)的情况下，调制效率的最大值为${\mu }_{AM}=\frac{1}{3}$，因此AM信号的功率利用率比较低。

• 输入噪声功率

对于高斯白噪声来说，由于高斯白噪声的双边功率谱密度为$\frac{n_0}{2}$，而其带宽无穷大，所以理想的高斯白噪声的功率是无穷大的，所以我们将其通过带通滤波器(传输函数为$1$)，将噪声带宽限制在滤波器的带宽$B$内

经过带通滤波器的噪声就近似于窄带高斯噪声，
$$\begin{array}{r}{n}_i(t)=n_c(t)cos{w}_{0}t-n_s(t)sin{w}_{0}t\end{array}$$噪声的功率为
$$\begin{array}{r}{N}_i={\bar{n}}_i^2(t)=n_{0}B\end{array}$$
5. 输入信噪比

由上文可知输入信号功率为载频功率和边带功率之和：$$\begin{array}{r}{S}_i=P_{AM}=\frac{1}{2}{A}^2+\frac{1}{2}{\bar{m}}^2(t)=P_c+P_s\end{array}$$输入噪声功率为：$$\begin{array}{r}{N}_i={\bar{n}}_i^2(t)=n_{0}B\end{array}$$于是输入信噪比为：$$\begin{array}{r}\frac{S_i}{N_i}=\frac{解调器输入已调信号的平均功率}{解调器输入噪声的平均功率}=\frac{P_{AM}}{N_i}=\frac{\frac{1}{2}[A^2+{\bar{m}}^2(t)]}{{\bar{n}}_i^2(t)}=\frac{P_c+P_s}{n_{0}B}\end{array}$$

2. 解调方式

解调是调制的逆过程，其作用是从接收的已调信号中恢复原基带信号(调制信号)。解调方法可以分为相干解调与非相干解调(包络检波)

（1）相干解调

调制是把基带信号的频谱搬移道了载频的位置，这一过程可以通过调制信号与载波信号相乘实现。而解调是调制的逆过程，需要把在载频为主的已调信号的谱搬回道原始的基带位置，这一过程仍然可以通过将已调信号与载波相乘来实现

1. 时域

接收端接收到已调信号$s_i(t)$，该信号域一个载波信号$cos{w}_{c}t$相乘，得到一个解调信号$s_p(t)$$$\begin{array}{r}{s}_p(t)=s_i(t)cos{w}_{c}t=s_m(t)cos{w}_{c}t=[A+m(t)]co{s}^2{w}_{c}t\end{array}$$解调后的信号包含一个高频分量和一个低频信号：
$$\begin{array}{r}{s}_p(t)=\frac{1}{2}[A+m(t)]cos2w_{c}t+\frac{1}{2}[A+m(t)]\end{array}$$用一个低通滤波器把高频成分滤掉，就得到了要传递的基带信号$\frac{1}{2}[A+m(t)]$；只是此时AM信号的解调结果中含有直流分量$A_0$，这时在解调后的信号加上一个隔直电容即可，最终的输出信号为：$s_i(t)=\frac{1}{2}m(t)$

2. 频域

已调信号与载波信号相乘后得到的解调信号$s_p(t)$的频域如下所示:$$\begin{array}{r}{S}_p(w)=\frac{\pi A}{2}[\delta (w+2w_c)+\delta (w-2w_c)]+\frac{1}{4}[M(w+2w_c)+M(w-2w_c)]+\pi A+\frac{1}{2}M(w)\end{array}$$然后使用一个低通滤波器把高频成分滤掉，就得到了要传递的基带信号$\frac{1}{2}M(w)+\pi A$，由于该信号存在直流分量，所以然后将该基带信号通过一个隔直电容，就得到了调制信号$\frac{1}{2}M(w)$。

3. 带宽

假设调制信号$s_m(t)$的带宽为$f_H$，易知传输信号带宽为$2f_H$，经过带通滤波器后，输入信号与载波相乘，其带宽为$3f_H$，然后通过低通滤波器，最终输出信号传输带宽为$f_H$

4. 功率

• 输出信号功率：

通过低通滤波器和电容后，解调器输出的有用信号为：$s_o(t)=m_o(t)=\frac{1}{2}m(t)$，输出端有用信号功率为$S_o={\bar{m}}_o^2(t)=\frac{1}{4}{\bar{m}}^2(t)$，其功率为调制信号功率的$\frac{1}{4}$，边带信号功率的$\frac{1}{2}$$$\begin{array}{r}{S}_o=\frac{1}{4}{\bar{m}}^2(t)=\frac{1}{4}{\bar{P}}_m=\frac{1}{2}{\bar{P}}_s\end{array}$$

• 输出噪声功率：

在解调信号时，噪声经过了接收端端带通滤波器，由于带通滤波器的带宽远小于其中心频率$w_0$，可将其视为窄带滤波器，此时噪声频谱集中在滤波器的中心频率$w_0$，也就是调制载频$w_c$附近，因此解调端收到的噪声就是平稳窄带高斯噪声，可以表示为：
$$\begin{array}{r}{n}_i(t)=n_c(t)cos{w}_{0}t-n_s(t)sin{w}_{0}t\end{array}$$它与载波$cos{w}_{c}t$相乘后，得：
$$\begin{array}{r}{n}_p(t)=n_i(t)cos{w}_{c}t=\frac{1}{2}{n}_c(t)+\frac{1}{2}[n_c(t)cos2w_{c}t-n_s(t)sin2w_{c}t]\end{array}$$经过低通滤波器去除高频分量后，解调器最终输出噪声为：
$$\begin{array}{r}{n}_o(t)=\frac{1}{2}{n}_c(t)\end{array}$$故输出噪声功率为：
$$\begin{array}{r}{N}_i={\bar{n}}_o^2(t)=\frac{1}{4}{\bar{n}}_c^2(t)\end{array}$$由随机过程的知识可知，窄带噪声$n_i(t)$及其同相分量$n_c(t)$和正交分量$n_s(t)$的均值为$0$，且具有相同方差，即$$\begin{array}{r}{n}_i^2(t)=n_c^2(t)=n_s^2(t)=N_i\end{array}$$其中$N_i$为解调器输入噪声功率，于是：$$\begin{array}{r}{N}_o=\frac{1}{4}{\bar{n}}_i^2(t)=\frac{1}{4}{N}_i=\frac{1}{4}{n}_{o}B\end{array}$$这里的$B=2f_H$指带通滤波器的带宽

5. 输出信噪比

由上文可知输出信号功率为：$$\begin{array}{r}{S}_o={\bar{m}}_o^2(t)=\frac{1}{4}{\bar{m}}^2(t)=\frac{1}{4}{\bar{P}}_m=\frac{1}{2}{\bar{P}}_s\end{array}$$输出噪声功率为：$$\begin{array}{r}{N}_o={\bar{n}}_o^2(t)=\frac{1}{4}{\bar{n}}_i^2(t)=\frac{1}{4}{N}_i=\frac{1}{4}{n}_{o}B\end{array}$$于是输出信噪比为：$$\begin{array}{r}\frac{S_o}{N_o}=\frac{解调器输出有用信号的平均功率}{解调器输出噪声的拼接功率}=\frac{{\bar{m}}_o^2(t)}{{\bar{n}}_o^2(t)}=\frac{{\bar{m}}^2(t)}{{\bar{n}}_i^2(t)}=\frac{{\bar{P}}_m}{n_{0}B}=\frac{2{\bar{P}}_s}{n_{0}B}\end{array}$$输出信噪比与调制方式和解调方式都密切相关。在已调信号平均功率相等，而且信道噪声功率谱密度相同的情况下，输出信噪比$S_o/N_o$反映了解调器的抗噪声性能。

6. 调制增益

为了便于比较同类调制系统采用不同的解调器时的性能，可以使用输出信噪比和输入信噪比的比值来表示：$$\begin{array}{r}G=\frac{S_o/N_o}{S_i/N_i}\end{array}$$这个比值$G$称为调制制度增益或信噪比增益

可以得到AM信号经过相干解调后的调制增益始终为
$$\begin{array}{r}G=\frac{2P_s}{P_c+P_s}\end{array}$$
7. 相干解调的难点

相干解调实现的关键是接收端要提供一个与载波信号同频同相的相干载波$cos{w}_{c}t$

常见的情况是，接收机产生了同频不同相的载波信号，且与原载波间的相位差为$\varphi$，此时得到的解调信号$s_{p1}$如下：
$$\begin{array}{r}{s}_p^{{}^{\prime }}(t)=S_i(t)cos(w_{c}t+\varphi )=[A+m(t)]cos(w_{c}t)cos(w_{c}t+\varphi )\end{array}$$$$\begin{array}{r}{s}_p^{{}^{\prime }}(t)=\frac{1}{2}[A+m(t)]cos(2w_{c}t)cos(\varphi )+\frac{1}{2}[A+m(t)]sin(2w_{c}t)sin(\varphi )+\frac{1}{2}[A+m(t)]cos(\varphi )\end{array}$$然后去除高频分量和直流分量得到：
$$\begin{array}{r}{s}_o=\frac{1}{2}m(t)cos(\varphi )\end{array}$$相位差使得解调信号在幅度上衰减了一个因子 $cos\varphi$，会使调制/原始基带信号减弱，甚至带来失真。

（2）包络检波

在AM调制中，加入直流分量是为了让调制后的信号全部为正数，也就是为了满足$|m(t){|}_{max}<=A_0$，此时解调器收到的输入信号$s_i(t)$的包络与调制信号$m(t)$的形状完全一样，此时对输入信号$s_i(t)$不仅可以使用相干解调，也可以使用包络检波；并且将$a=\frac{|m(t){|}_{max}}{A_0}$称为调幅系数

当$a<1$，称调制过程为正常调幅
当$a=1$，称其调制过程为满调幅
当$a<1$，称其调制过程为过调幅，此时使用包络检波就会发生失真，可以采用相干解调的方法

包络检波的电路如下：

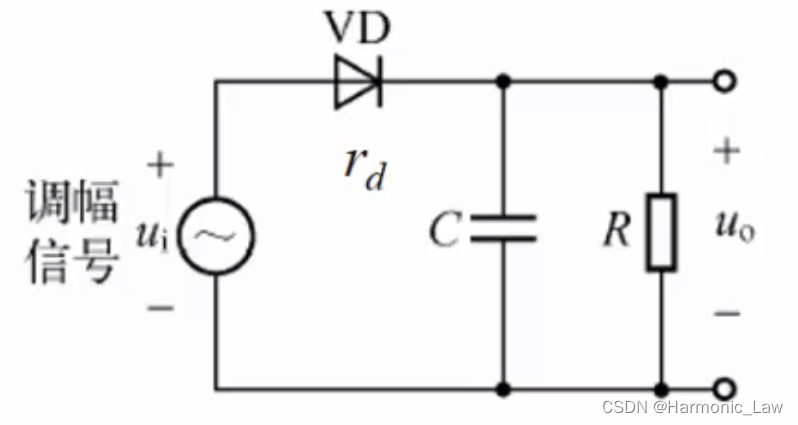
• 二极管单向导通，只有输入电压$u_i$大于开启电压是才导通，开启电阻为$r_d$
• $R$为大电阻，保证底盘电压尽量大幅值输出
• C为高频旁路电容，保证对高频信号短路，避免从$R$上输出，起到低频滤波作用
• 由于$r_d$较小，因此电容C的充电时间常数$r_{d}C<<RC$，也就是说充电的时间常数小，放电的充电常数比较大，也就是充电快，放电慢

输出电压是电容$C$俩端的电压，所以我们来分析电容俩端电压的变化。

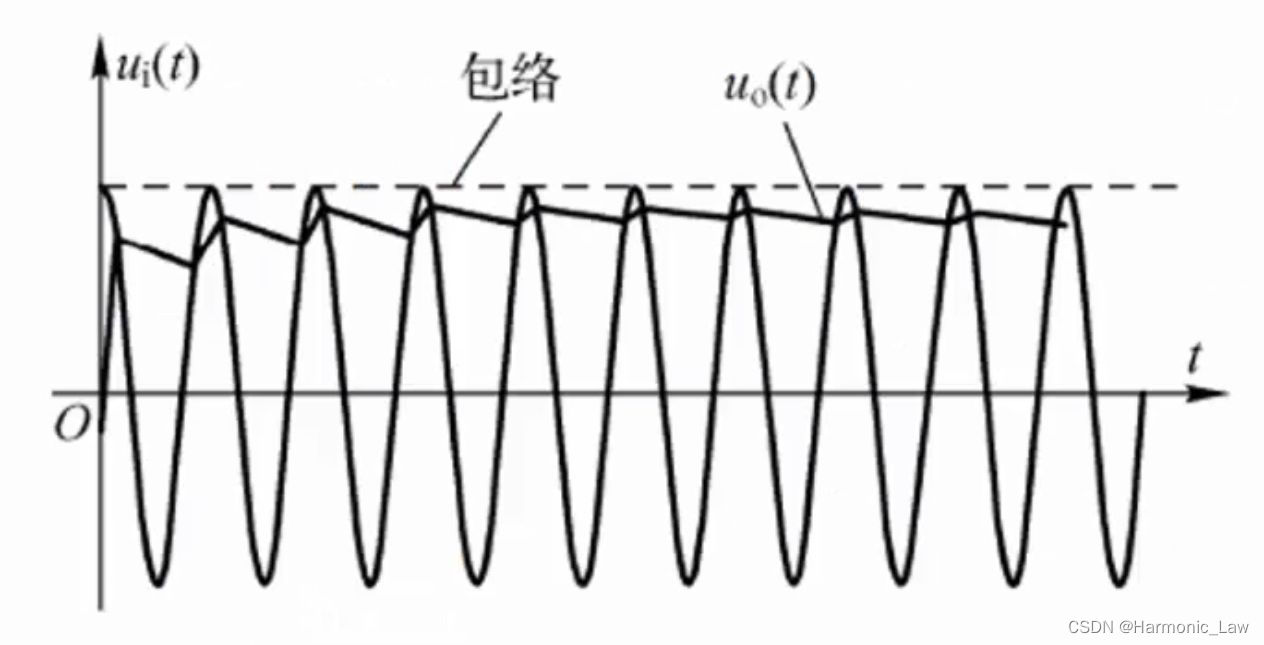
原理：假设输入的电压$u_i$是等幅的正弦波，电路开启时，由于电容$C$上没有电压，因此电容$C$会快速充电，直到电容上的电压等于输入电压为止，当输入电压逐渐下降，并且输入电压小于电容俩端电压后，二极管截止，电容$C$开始放电，由于$RC$较大，电容放电缓慢，电容俩端电压(输出电压)可以几乎保持不变。下一个周期电压再次逐渐增加，当$u_i>u_o$时，二极管导通，继续为电容快速充电，输出$u_o$快速增加，然后再次缓慢下降，一直这样持续下去。

由此可见，输出电压$u_o$几乎保持在输入信号峰值的位置，这种检波方式称为峰值检波

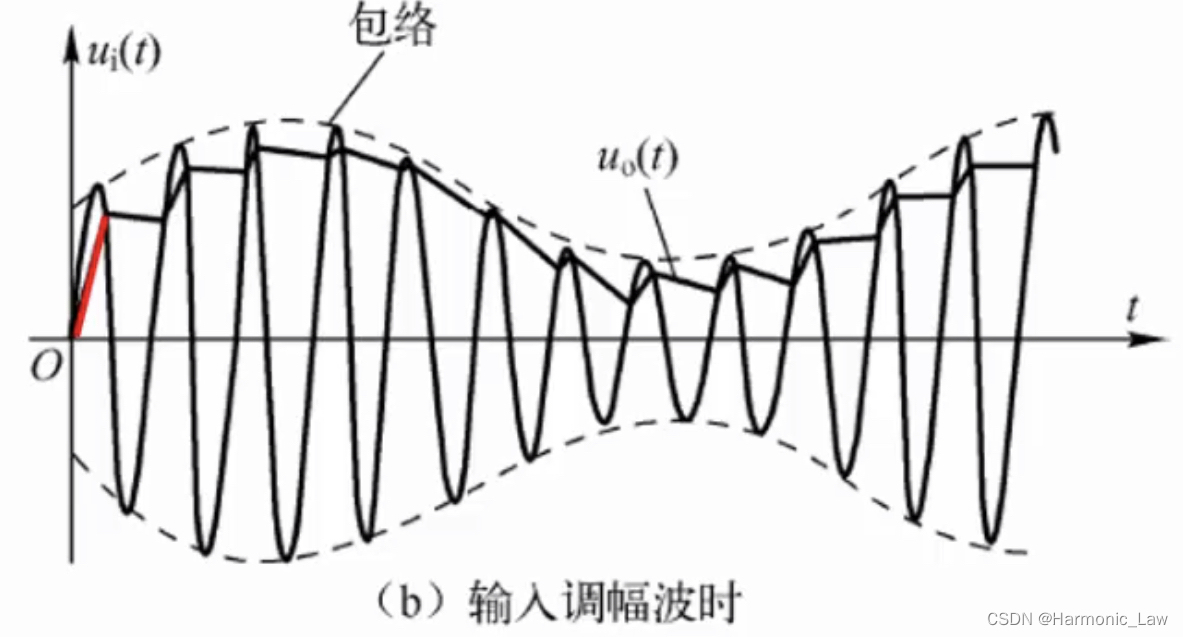
原理：当输入信号为$AM$调幅波时，检波过程与正弦波的检波过程相同；即电路导通时，电容$C$快速充电，直到电容俩端电压等于输入电压；当输入电压逐渐下降时，并且$u_i<u_o$时，二极管截止，电容放电，由于放电比较慢，输出电压$u_o$几乎保持不变；下一个周期，$u_i$逐渐增加，当$u_i>u_o$时二极管导通，电容充电，输出$u_o$快速增加，然后再次缓慢放电。

注意：由于输入信号为调幅波信号，所以下一个峰值可能小于前一个峰值，充电时间可能非常短。此时的电容不可以放电太快，否则会使输出电压$u_o$无法保持在峰值处；电容也不可以放电太慢，否则会使输出电压$u_o$跟不上调幅波的降低。所以具体电路中需要根据调幅波的频率设置合适的$R$和$C$

合理设置$RC$，让$RC>>\frac{1}{w_c}$，就可以滤出$w_c$及以上的频率成分，只留下调制信号的频率成分及更低的频率成分，就可以恢复出包络

我们发现，包络检波就是直接从已调波的幅度中提取原调制信号，其结构简单，只需要一些基本的电路即可实现，而且解调输出时相干解调输出的俩倍。

三、DSB调制解调原理及抗噪声性能分析

DSB调制解调过程几乎域AM调制解调过程相同，我们只需要知道哪些数据发生了变化即可

在$AM$信号中，载波分量不携带信息，信息完全由边带传输。如果在$AM$调制模型中将直流$A_0$去掉，那么就可以得到一种高调制效率的调制方式，即抑制载波双边带信号(DSB-SC)，简称双边带信号(DSB)；其信号其时频域表达式如下：
$$\begin{array}{r}{s}_{DSB}(t)=m(t)cos{w}_{c}t\end{array}$$$$\begin{array}{r}{S}_{DSB}(w)=\frac{1}{2}[M(w+w_c)+M(w-w_c)]\end{array}$$与AM信号相比，由于不存在载波分量，所以其调制效率${\mu }_{DSB}=100$%，即全部功率用于信息传输。但是，由于没有了直流分量$A_0$，所以$DSB$信号的包络不在与调制信号的变化一直，那么就不能采用包络检波，应该采用相干解调。

在经过带通滤波器后与载波信号相乘，其信号的时频域表达式如下
$$\begin{array}{r}{s}_p(t)=m(t)co{s}^2{w}_{c}t=\frac{1}{2}m(t)cos2w_{c}t+\frac{1}{2}m(t)\end{array}$$$$\begin{array}{r}{S}_p(w)=\frac{1}{4}[M(w+2w_c)+M(w-2w_c)]+\frac{1}{2}M(w)\end{array}$$与AM信号相比，由于不存在直流分量，所以在不需要将得到的信号通过隔直电容，只需要使用一个低通滤波器把高频成分滤掉，就得到了调制信号$\frac{1}{2}m(t)$。

而噪声在此过程中与$AM$调制解调中的值相同，不在赘述

总结：不变的量与变化的量

四、SSB调制解调及抗噪声分析

$DSB$信号虽然节省载波功率，减少了输入信噪比/输入信号功率，提高了调制增益$G$，但是它所需要的传输带宽依然是调制信号的带宽的俩倍，即其传输带宽与$AM$信号带宽相同，能否在$DSB$信号的基础上进行改进减少其传输带宽呢？

我们注意到$DSB$信号俩个边带中的任意一个都包含了$M(w)$都所有频率成分，因此我们只需要传输一个边带即可，这样既可以节省发送功率，还可以节省$1/2$的传输带宽，这种方式就称为单边带调制。

1. 希尔伯特变换

希尔伯特变换就是把信号中的正频率分量相移$-\frac{\pi }{2}$，信号功率保持不变

例：若$f(t)=cos{w}_{c}t$，则$f(t)$的希尔伯特变换为$\hat{f}(t)=cos(w_{c}t-\frac{\pi }{2})=sin{w}_{c}t$，则其传输函数为：

即$H_h(f)=-jsgn(f)$，其时域表达式为$h(t)=\frac{1}{\pi t}$

所以时域希尔伯特变换公式如下：
$$\begin{array}{r}\hat{f}(t)=f(t)\ast h(t)=f(t)\ast \frac{1}{\pi t}\end{array}$$频域的希尔伯特变换公式为：
$$\begin{array}{r}\hat{F}(f)=F(f)[-jsgn(f)]\end{array}$$

2. 单边带信号的产生(相移法)

对于任意调制信号$m(t)$，根据傅立叶级数可以知道它可以表示为余弦信号的线性叠加，所以设调制信号为：
$$\begin{array}{r}m(t)=\sum _i{m}_{i}cos{w}_{i}t\end{array}$$设载波为：$$\begin{array}{r}c(t)=cos{w}_{c}t\end{array}$$那么已调信号为：
$$\begin{array}{r}{s}_m(t)=m(t)c(t)=\frac{1}{2}\sum _i{m}_{i}cos(w_c-w_i)t+\frac{1}{2}\sum _i{m}_{i}cos(w_c+w_i)t\end{array}$$可以看出$s_m(t)$的俩项分别对应上下俩个边带，下边带和上边带表达式如下：
$$\begin{array}{r}{s}_{LSB}(t)=\frac{1}{2}\sum _i{m}_{i}cos(w_c-w_i)t=\frac{1}{2}\sum _i{m}_{i}cos{w}_{i}tcos{w}_{c}t+\frac{1}{2}\sum _i{m}_{i}sin{w}_{i}tsin{w}_{c}t=\frac{1}{2}m(t)cos{w}_{c}t+\frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$$$\begin{array}{r}{s}_{USB}(t)=\frac{1}{2}\sum _i{m}_{i}cos(w_c+w_i)t=\frac{1}{2}m(t)cos{w}_{c}t-\frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$其系统框图如下：

3. SSB调制解调及抗噪声性能分析

（1）调制

假设调制信号 $m(t)$ 的均值为0，然后与载波$c(t)$相乘，就得到了调幅信号 $s_m(t)$，改信号是一个双边带信号，该信号$s_m(t)$再经过一个边带滤波器，消除不要的边带，即可得到单边带信号$S_{SSB}(t)$；$S_{SSB}(t)$信号然后通过传输信道，与噪声 $n(t)$ 叠加，接收端得到 $n(t)+S_{SSB}(t)$，此时将该信号通过带通滤波器，然后就得到接收端的输入信号 $s_i(t)$ 和接收端的输入噪声 $n_i(t)$

1. 时域

调制信号 $m(t)={\sum }_i{m}_{i}cos{w}_i(t)$ 与载波$c(t)=cos{w}_{c}t$相乘，就得到了调幅信号 $s_{DSB}(t)$
$$\begin{array}{r}{s}_{DSB}(t)=m(t)c(t)=\sum _i{m}_{i}cos{w}_{i}tcos{w}_{c}t=\frac{1}{2}\sum _i{m}_{i}cos(w_c+w_i)t+\frac{1}{2}\sum _i{m}_{i}cos(w_c-w_i)t\end{array}$$该$S_{DSB}(t)$信号是一个双边带信号，包括上下俩个边带，将其通过一个边带滤波器。可以看出$S_{DSB}(t)$的俩项分别对应上下俩个边带，下边带和上边带表达式如下：$$\begin{array}{r}{s}_{LSB}(t)=\frac{1}{2}\sum _i{m}_{i}cos(w_c-w_i)t=\frac{1}{2}m(t)cos{w}_{c}t+\frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$$$\begin{array}{r}{s}_{USB}(t)=\frac{1}{2}\sum _i{m}_{i}cos(w_c+w_i)t=\frac{1}{2}m(t)cos{w}_{c}t-\frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$综合表示为：$$\begin{array}{r}{s}_{SSB}(t)=\frac{1}{2}m(t)cos{w}_{c}t\pm \frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$其中$"-"$表示上边带信号，$“+”$表示下边带信号。

然后该$SSB$信号通过带通滤波器后输入接收端，假设滤波器传输函数为$1$，则$s_i=s_{SSB}$

2. 频域

调制信号 $m(t)$ 与载波$c(t)=cos{w}_{c}t$相乘，就得到了调幅信号，其频域 $S_{DSB}(w)$表达式如下所示：$$\begin{array}{r}{S}_{DSB}(w)=\frac{1}{2}[M(w+w_c)+M(w-w_c)]\end{array}$$将双边信号$S_{DSB}(w)$通过如下单边滤波器，就可以得到下边带$S_{SSB}(w)$

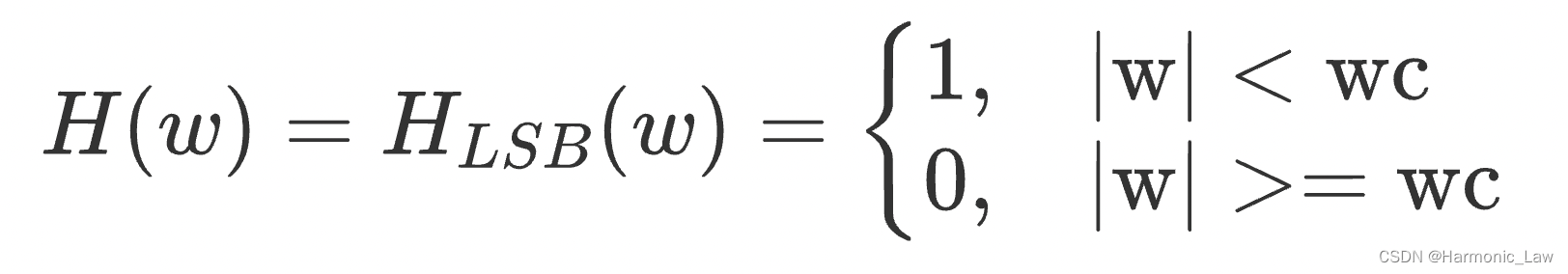
3. 带宽

假设调制信号$s_m(t)$的带宽为$f_H$，与载波相乘后得到双边带信号，其贷款为$2f_H$，经过单边带滤波器后得到单边带信号，由于单边带滤波器的带宽为双边带带通滤波器的带宽的一半，可知SSB信号传输带宽为$B=f_H$

4. 输入信号功率

单边信号$s_{SSB}(t)$经过信道和带通滤波器，假设带通滤波器传输函数为$1$，输入信号为：$$\begin{array}{r}{s}_i(t)=s_{SSB}(t)=\frac{1}{2}m(t)cos{w}_{c}t\pm \frac{1}{2}\hat{m}(t)sin{w}_{c}t\end{array}$$其功率如下：$$\begin{array}{r}{S}_i=S_{SSB}={\bar{s}}_i^2(t)=\frac{1}{4}{\bar{m}}^2(t)=\frac{1}{4}{P}_m\end{array}$$

• 输入噪声功率

与双边带信号输入噪声功率相同$N_i=n_{0}B$，其中$B$为带通滤波器带宽

5. 输入信噪比

由上文可知输入信号功率为载频功率和边带功率之和：$$\begin{array}{r}{S}_i=P_{SSB}=\frac{1}{4}{\bar{m}}^2(t)=\frac{1}{4}{P}_m\end{array}$$输入噪声功率为：$$\begin{array}{r}{N}_i={\bar{n}}_i^2(t)=n_{0}B\end{array}$$于是输入信噪比为：$$\begin{array}{r}\frac{S_i}{N_i}=\frac{\frac{1}{4}{\bar{m}}^2(t)}{{\bar{n}}_i^2(t)}=\frac{\frac{1}{4}{P}_m}{n_{0}B}=\frac{{\bar{m}}^2(t)}{4n_{0}B}\end{array}$$

（2）解调

$SSB$信号单解调方法与$DSB$信号相同，其区别仅在于解调器之前的带通滤波器的带宽和中心频率不同。$SSB$信号使用的带通滤波器的带宽是$DSB$信号使用的带通滤波器的带宽的2倍，即$B_{SSB}=\frac{1}{2}{B}_{DSB}$。

$s_{SSB}(t)$信号到达接收端作为$s_i(t)$与载波$cos{w}_{c}t$相乘后，得：
$$\begin{array}{r}{s}_p(t)=s_i(t)cos{w}_{c}t=\frac{1}{4}m(t)+\frac{1}{4}[m(t)cos2w_{c}t-\bar{m}(t)sin2w_{c}t]\end{array}$$经过低通滤波器去除高频分量后，解调器最终输出信号为：
$$\begin{array}{r}{m}_o(t)=\frac{1}{4}m(t)\end{array}$$故输出信号功率为：
$$\begin{array}{r}{S}_o={\bar{m}}_o^2(t)=\frac{1}{16}{\bar{m}}^2(t)\end{array}$$

而噪声输出功率与$DSB$解调时噪声输出功率相同：$$\begin{array}{r}{N}_o=\frac{1}{4}{\bar{n}}_i^2(t)=\frac{1}{4}{N}_i=\frac{1}{4}{n}_{o}B\end{array}$$这里的$B=f_H$指$SSB$信号使用的带通滤波器的带宽

所以输出信噪比为：
$$\begin{array}{r}\frac{S_o}{N_o}=\frac{1/16{\bar{m}}^2(t)}{1/4{\bar{n}}_{0}B}=\frac{1/16{\bar{P}}_m}{1/4{\bar{N}}_i}=\frac{{\bar{m}}^2(t)}{4n_{0}B}\end{array}$$可以得到SSB信号经过相干解调后的调制增益始终为
$$\begin{array}{r}G=\frac{S_o/N_o}{S_i/N_i}=1\end{array}$$易知$G_{DSB}$=$2G_{SSB}$，但是这不能说明DSB系统的抗早上性能比SSB系统好！因为二者的输入信号功率不同，传输信号带宽不同，在相同噪声功率谱密度下，输入噪声功率不同(由于SSB信号传输带宽是DSB传输信号带宽一半)；所以二者的输出信噪比是在不同的条件下得到的。

如果我们在相同的输入信号功率$S_i$，相同的输入噪声功率谱密度$\frac{n_0}{2}$，相同的传输带宽/基带信号带宽$B=f_H$条件下，对二者的调制方式进行比较，可以发送二者的输出信噪比是相等的，也就是说二者的抗再说性能是相同的。但是由于SSB信号所需的传输带宽是DSB信号的$1/2$，所以SSB得到普遍使用