图的表示常见到的有：

• 相邻矩阵法
• 相邻表法

（1）相邻矩阵法
有多少个顶点（n）就用多少长度的二维数组（arr[n][n]）来表示图，某个点arr[x][y]值为1则表示对应顶点有边存在，为0则表示对应顶点无边存在。
一个简单的例子展示：

public class NeighburArr {
    public static void main(String[] args) {
        int[][] arr = new int[5][5];
        int i, j, tmpi, tmpj;
        int data[][] = {{1,2}, {2,1}, {2,3}, {2,4}, {4,3}};
        for(i=0;i<5;i++) {
            for(j=0;j<5;j++) {
                arr[i][j] = 0;
            }
        }
        for (i=0;i<5;i++) {
            tmpi = data[i][0];
            tmpj = data[i][1];
            arr[tmpi][tmpj] = 1;
        }
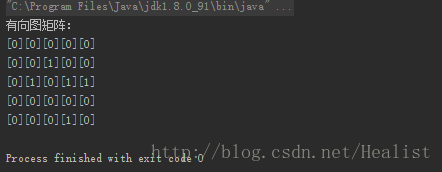
        System.out.println("有向图矩阵：");
        for (i=0;i<5;i++) {
            for(j=0;j<5;j++) {
                System.out.print("[" + arr[i][j] + "]");
            }
            System.out.println();
        }
    }
}

(2)相邻表法
图形A有n个顶点，则用n个表（链表）来表示，每个顶点后面接着的表节点元素表示该顶点到该元素存在边，每个表的最后一个元素为null。

一个例子展示：

class Node {
    int x;
    Node next;
    public Node(int x){
        this.x = x;
        this.next = null;
    }
}
public class GraphLink {
    public Node first;
    public Node last;
    public boolean isEmpty() {
        return first == null;
    }
    public void print() {
        Node current = first;
        while(current != null) {
            System.out.print("[" + current.x + "]");
            current = current.next;
        }
        System.out.println();
    }
    public void insert(int x) {
        Node newNode = new Node(x);
        if(this.isEmpty()) {
            first = newNode;
            last = newNode;
        }
        else {
            last.next = newNode;
            last = newNode;
        }
    }

    public static void main(String[] args) {
        int Data[][] = { {1,2}, {2,1}, {1,5}, {5,1}, {2,3}, {3,2}, {2,4},
                {4,2}, {3,4}, {4,3}, {3,5}, {5,3}, {4,5}, {5,4} };
        int DataNum = 0;
        int i=0, j=0;
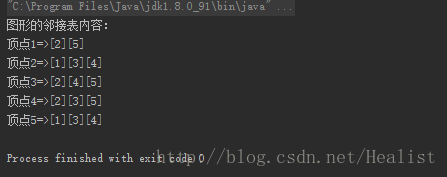
        System.out.println("图形的邻接表内容：");
        GraphLink head[] = new GraphLink[6];
        for(i=1;i<6;i++) {
            head[i] = new GraphLink();
            System.out.print("顶点" + i + "=>");
            for(j=0; j<14;j++) {
                if(Data[j][0] == i) {
                    DataNum = Data[j][1];
                    head[i].insert(DataNum);
                }
            }
            head[i].print();
        }
    }

}