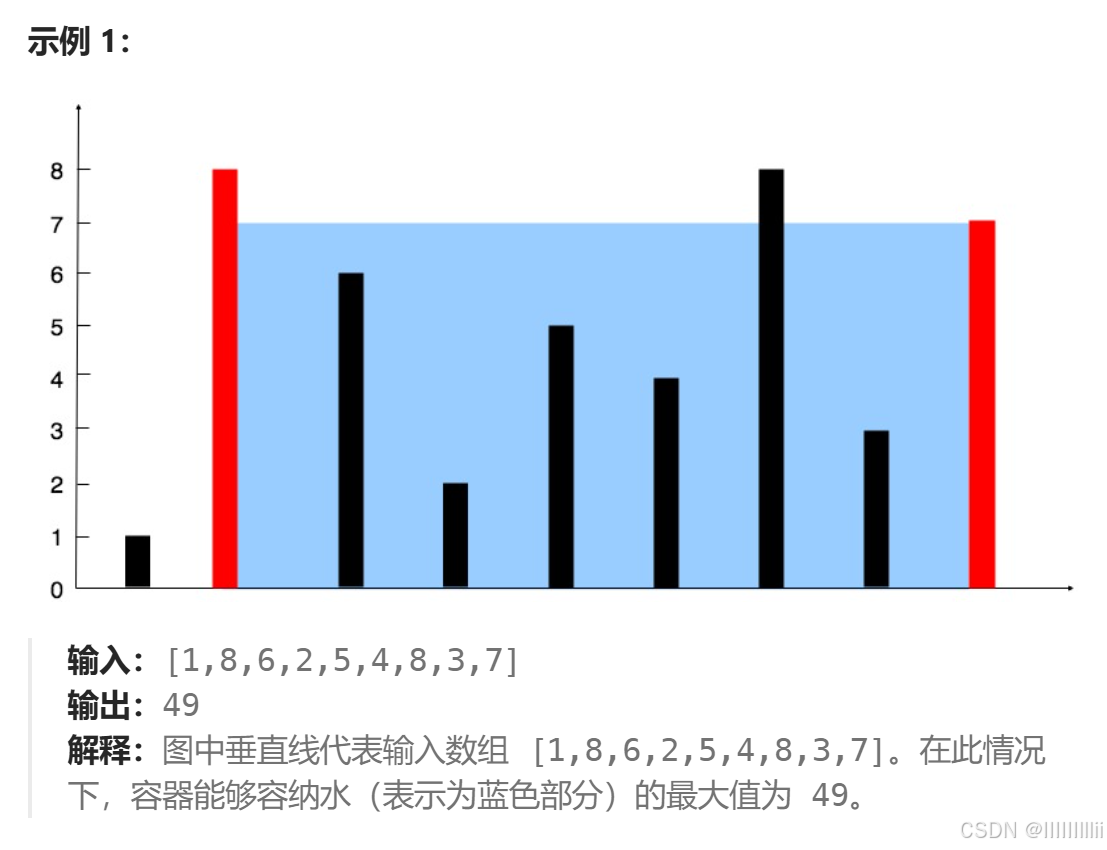
ps:题目来自力扣

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

class Solution {
    public int maxArea(int[] height) {
        // 初始化两个指针，left 指向数组的起始位置，right 指向数组的末尾位置
        int left = 0;
        int right = height.length - 1;
        // 初始化最大水量为 0
        int maxWater = 0;

        // 只要 left 小于 right，就继续循环
        while (left < right) {
            // 计算当前两条垂线与 x 轴构成的容器的宽度
            int width = right - left;
            // 计算当前两条垂线中较短的那条垂线的高度
            int currentHeight = Math.min(height[left], height[right]);
            // 计算当前容器的水量
            int currentWater = width * currentHeight;
            // 更新最大水量
            maxWater = Math.max(maxWater, currentWater);

            // 移动指针：较短的垂线对应的指针向内移动
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return maxWater;
    }
}

代码解释

本题要求在给定的整数数组 height 中找出两条垂线，使得它们与 x 轴共同构成的容器可以容纳最多的水。我们可以使用双指针法来解决这个问题。

具体步骤

1. 初始化指针和最大水量：
   • 定义两个指针 left 和 right，分别初始化为数组的起始位置和末尾位置。
   • 定义一个变量 maxWater 用于存储最大水量，初始值为 0。
2. 循环计算水量并移动指针：
   • 使用 while 循环，只要 left 小于 right，就继续循环。
   • 在每次循环中：
     • 计算当前容器的宽度 width，即 right - left。
     • 计算当前两条垂线中较短的那条垂线的高度 currentHeight，使用 Math.min(height[left], height[right])。
     • 计算当前容器的水量 currentWater，即 width * currentHeight。
     • 更新 maxWater，使用 Math.max(maxWater, currentWater)。
     • 移动指针：如果 height[left] < height[right]，将 left 指针向右移动一位；否则，将 right 指针向左移动一位。
3. 返回结果：
   • 当循环结束后，maxWater 中存储的就是最大水量，将其返回。