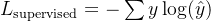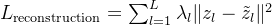Ladder Networks 是一种半监督学习模型,通过将无监督学习与监督学习相结合,在标记数据较少的情况下实现高效的学习。它最初由 A. Rasmus 等人在 2015 年提出,特别适合深度学习任务,如图像分类或自然语言处理。
核心思想
Ladder Networks 的目标是利用标记和未标记数据来优化网络性能。其关键思想是引入噪声对网络进行训练,同时通过解码器恢复被破坏的数据结构。它主要由以下三部分组成:
-
编码器(Encoder):
编码器是一个有噪声的前馈神经网络,用于从输入数据生成潜在表示。噪声会加入到各个层的激活值中。 -
解码器(Decoder):
解码器尝试从有噪声的编码器的潜在表示重建无噪声的输入数据。这个过程可以视为自编码器的一部分。 -
损失函数(Loss Function):
损失由两部分组成:- 监督损失: 使用标记数据计算的分类误差(如交叉熵)。
- 重建损失: 解码器重建无噪声表示与原始无噪声数据之间的误差。
通过联合优化这两部分,网络能够同时进行监督学习和无监督学习。
模型架构
Ladder Networks 的架构如下:
- 输入数据经过多层网络,每一层引入噪声,生成一个有噪声的激活值。
- 解码器逐层重建这些激活值,最终输出重建的输入。
- 使用标记数据进行分类任务,用未标记数据训练解码器,增强表示学习能力。
模型使用跳跃连接(Skip Connections)来帮助解码器更好地恢复无噪声表示。
损失函数
损失函数分为两部分:
-
监督损失:
使用分类任务中的标记数据,例如交叉熵: -
重建损失:
解码器的重建误差,例如均方误差:其中,
是无噪声激活值,
是有噪声的激活值的解码结果,
是每一层的权重。
总损失是两者的加权和:
优势
-
高效利用未标记数据:
通过重建误差,未标记数据在网络训练中也能发挥作用。 -
鲁棒性增强:
加入噪声训练有助于防止过拟合,提高网络的泛化能力。 -
层间交互建模:
跳跃连接有助于捕获层间复杂的相互关系,从而提高表示能力。
应用
-
图像分类:
在 MNIST、CIFAR-10 等数据集上表现优异,尤其在标记样本少的情况下。 -
半监督学习:
在需要结合标记数据和未标记数据的任务中具有广泛应用。 -
自然语言处理:
用于词嵌入学习或序列生成任务。
示例代码
以下是基于 TensorFlow 的 Ladder Networks 简化实现:
import tensorflow as tf
from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.models import Model, Sequential
# 噪声函数
def add_noise(x, noise_std=0.3):
return x + tf.random.normal(tf.shape(x), stddev=noise_std)
# 编码器
def encoder(input_dim, latent_dim, noise_std=0.3):
model = Sequential([
Dense(128, activation='relu', input_dim=input_dim),
Dropout(0.3),
Dense(latent_dim, activation='relu'),
tf.keras.layers.Lambda(lambda x: add_noise(x, noise_std=noise_std))
])
return model
# 解码器
def decoder(latent_dim, output_dim):
model = Sequential([
Dense(128, activation='relu', input_dim=latent_dim),
Dense(output_dim, activation='sigmoid') # 重建输入
])
return model
# 输入维度
input_dim = 784 # MNIST 数据集
latent_dim = 64
output_dim = input_dim
# 构建模型
encoder_model = encoder(input_dim, latent_dim)
decoder_model = decoder(latent_dim, output_dim)
# 输入数据
input_data = tf.keras.Input(shape=(input_dim,))
latent_repr = encoder_model(input_data)
reconstructed = decoder_model(latent_repr)
# 定义完整模型
ladder_network = Model(inputs=input_data, outputs=reconstructed)
ladder_network.compile(optimizer='adam', loss='mse')
# 示例训练
(X_train, _), (_, _) = tf.keras.datasets.mnist.load_data()
X_train = X_train.reshape(-1, 784).astype('float32') / 255.0
ladder_network.fit(X_train, X_train, epochs=10, batch_size=128)
输出结果
Epoch 1/10
469/469 [==============================] - 2s 3ms/step - loss: 0.0471
Epoch 2/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0271
Epoch 3/10
469/469 [==============================] - 2s 3ms/step - loss: 0.0233
Epoch 4/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0215
Epoch 5/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0204
Epoch 6/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0197
Epoch 7/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0191
Epoch 8/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0186
Epoch 9/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0182
Epoch 10/10
469/469 [==============================] - 1s 3ms/step - loss: 0.0178