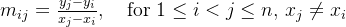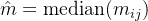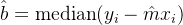【机器学习】鲁棒（健壮）回归-Theil-Sen估计（Theil-Sen Estimator）

Theil-Sen估计

Theil-Sen估计是一种用于线性回归的非参数方法，其优点是对离群点具有鲁棒性。它通过计算数据点之间所有可能斜率的中位数来估计回归线的斜率，随后使用这些斜率估算截距。

核心思想

斜率估计：对于给定的一组数据点 $(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)$ ，Theil-Sen 方法计算每对数据点之间的斜率：
$m_{ij} = \frac{y_j - y_i}{x_j - x_i}, \quad \text{for } 1 \leq i < j \leq n, \, x_j \neq x_i$
斜率 m 的估计值为这些 $m_{ij}$ 的中位数：
$\hat{m} = \text{median}(m_{ij})$
截距估计：截距 b 的估计值是使得中位残差最小的值。通常计算为：
$\hat{b} = \text{median}(y_i - \hat{m} x_i)$
回归方程：最终的回归方程为：
$y = \hat{m}x + \hat{b}$

优缺点

优点：

鲁棒性：对离群点不敏感，适用于数据中包含异常值的场景。
非参数性：不需要对误差分布作假设。

缺点：

计算复杂度：由于需要计算所有点对的斜率，其复杂度为，对于大数据集可能较慢。
仅限一维：适用于单变量回归，不适合多元回归。

Theil-Sen估计的Python实现

以下是使用 scipy.stats 库实现 Theil-Sen 回归的代码示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor

# 示例数据
np.random.seed(42)
X = np.random.rand(100) * 10  # 随机生成自变量
y = 2 * X + np.random.normal(0, 1, 100)  # 线性关系 + 噪声

# 添加一些离群点
X = np.append(X, [8, 9, 10])
y = np.append(y, [30, 35, 40])

plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False

# 可视化数据
plt.scatter(X, y, color="blue", label="数据点")
plt.xlabel("X")
plt.ylabel("y")
plt.title("带离群点的数据")
plt.show()

# 使用 Theil-Sen 方法进行回归
X = X.reshape(-1, 1)  # 调整为二维数组
model = TheilSenRegressor(random_state=42)
model.fit(X, y)

# 获取拟合结果
y_pred = model.predict(X)
print(f"斜率 (m): {model.coef_[0]:.2f}")
print(f"截距 (b): {model.intercept_:.2f}")

# 绘制结果
plt.scatter(X, y, color="blue", label="数据点")
plt.plot(X, y_pred, color="red", label="Theil-Sen回归线")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.title("Theil-Sen 回归结果")
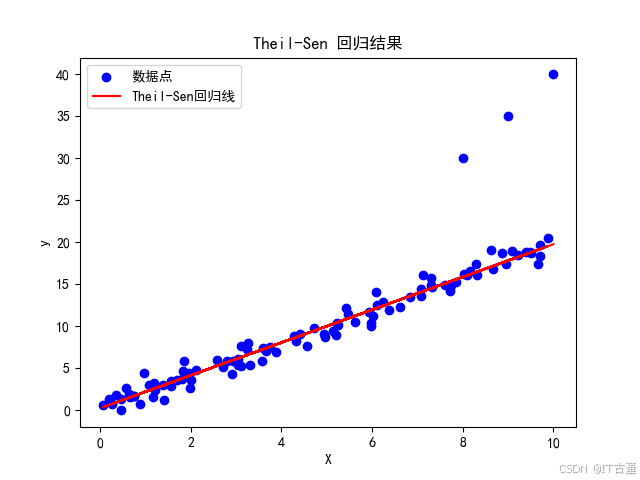
plt.show()

输出示例

回归方程：
- 输出拟合直线的斜率和截距，例如：
```
斜率 (m): 1.95
截距 (b): 0.25
```
图形结果：
- 数据点（含离群点）用蓝色散点表示。
- Theil-Sen拟合的回归线用红色直线表示。

应用领域

经济学：
- 分析具有极值或异常值的时间序列数据。
环境科学：
- 估计气候趋势或环境变量的变化。
计算机视觉：
- 图像配准中的鲁棒线性模型拟合。

Theil-Sen 估计常用场景包括需要处理离群点或非正态分布误差的数据。

【机器学习】鲁棒（健壮）回归-Theil-Sen估计（Theil-Sen Estimator）

Theil-Sen估计

核心思想

优缺点

优点：

缺点：

Theil-Sen估计的Python实现

输出示例

应用领域

悦读