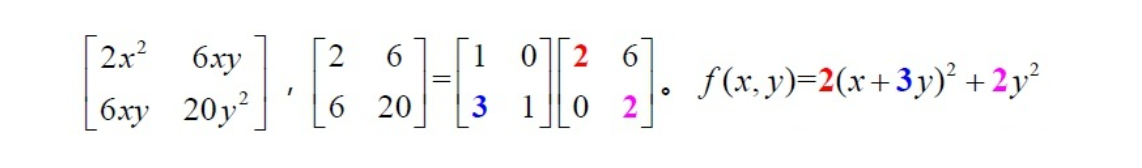正定矩阵Positive definite matrice
之前说过,正定矩阵是一类特殊的对称矩阵:
- 正定矩阵满足对称矩阵的特性(特征值为实数并且拥有一套正交特征向量、正 / 负主元的数目等于正 / 负特征值的数目)
- 另外,正定矩阵还具有更好的性质(所有特征值都为正实数、所有主元都为正实数、左上角的所有任意k阶(1<=k<=n)顺序主子式均为正)
注意,“正定”这一说法的前提,一定是“对称矩阵”
- 原因:提出正定矩阵的概念,主要是用于研究二次型
而任意n阶矩阵 B \boldsymbol{B} B给出的二次型 x T B x \mathbf{x}^{T} \boldsymbol{B} \mathbf{x} xTBx,都可以被化为对称矩阵 A = 1 2 ( B + B T ) \boldsymbol{A}=\frac{1}{2}(\boldsymbol{B}+\boldsymbol{B}^T) A=21(B+BT)给出的等价的二次型 1 2 x T ( B + B T ) x = x T B x \frac{1}{2}\mathbf{x}^{T}(\boldsymbol{B}+\boldsymbol{B}^T)\mathbf{x}=\mathbf{x}^{T} \boldsymbol{B} \mathbf{x} 21xT(B+BT)x=xTBx
同理,在复数域,提到正定矩阵,前提一定是Hermite矩阵
如何判定正定矩阵?
对于实对称矩阵,满足下列条件中任意一个(均为充要条件),就是正定矩阵:
- 满足二次型
x
T
A
x
>
0
(
x
≠
0
)
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0)
xTAx>0(x=0)
可以看出,此定义并不要求 A \boldsymbol{A} A是对称阵,然而一般情况下均默认正定矩阵是对称的(因为正定源于二次型,而二次型的矩阵一定对称) - 所有特征值为正实数
推论:正定矩阵 A \boldsymbol{A} A的逆矩阵 A − 1 \boldsymbol{A}^{-1} A−1,也是正定的(逆矩阵 A − 1 \boldsymbol{A}^{-1} A−1的特征值就是 A \boldsymbol{A} A特征值的倒数,必然也全为正)
正定矩阵的一套正交特征向量,可以张成整个空间,空间中任意向量可以表示为 x = c 1 x 1 + c 2 x 2 + … c n x n \mathbf{x}=c_{1} \mathbf{x}_{1}+c_{2} \mathbf{x}_{2}+\ldots c_{n} \mathbf{x}_{n} x=c1x1+c2x2+…cnxn,根据 A x = λ x \boldsymbol{A} \mathbf{x}=\lambda \mathbf{x} Ax=λx,得到 x T A x = c 1 2 λ 1 + c 2 2 λ 2 + … c n 2 λ n \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=c_{1}^{2} \lambda_{1}+c_{2}^{2} \lambda_{2}+\ldots c_{n}^{2} \lambda_{n} xTAx=c12λ1+c22λ2+…cn2λn,因此必须所有特征值为正,才能保证正交 x T A x > 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0) xTAx>0(x=0)
- 对矩阵消元后,所有主元为正实数
后面将会看到,二次型对应一个二次多项式,对多项式配方可以轻易看出相应的图像的形状,要保证正交,即图像 x T A x > 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 \quad(\mathbf{x}\neq 0) xTAx>0(x=0),那么要求配方后的所有完全平方项的系数都为正,这些配方后的系数刚好就是消元后的主元!
- 左上角的所有任意k阶(1<=k<=n)顺序主子式为正
i.e. 矩阵左上角所有子矩阵的行列式为正
A \mathbf A A正定,左上角的各个子矩阵 A k \mathbf A_k Ak必然正定: x T A x = [ x k 0 ] [ A k ∗ ∗ ∗ ] [ x k 0 ] = x k T A k x k \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} =\left[\begin{array}{ll}x_{k} & 0\end{array}\right] \left[\begin{array}{cc} A_{k} & * \\* & *\end{array}\right] \left[\begin{array}{c}x_{k} \\0\end{array}\right] =\mathbf{x}_{k}^{T} \boldsymbol{A}_{k} \mathbf{x}_{k} xTAx=[xk0][Ak∗∗∗][xk0]=xkTAkxk
第1条为正定矩阵的定义,其余三条一般用于验证正定性;
正定矩阵的几何意义:二次型
将表达式 x T A x \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} xTAx称为二次型(quadratic form)
之所以称为二次型,是因为整个式子的计算结果为二次多项式(不含线性一次项)
二次型的几何意义
若 x = [ x 1 x 2 ] \mathbf{x}=\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right] x=[x1x2]含有两个变量,则二次型 x T A x \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} xTAx可以对应到三维空间中的某个曲面 x T A x \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} xTAx
举例:
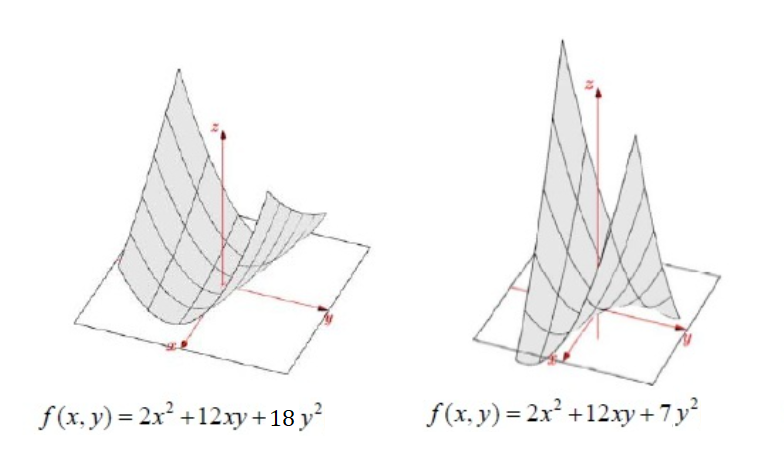
- A = [ 2 6 6 20 ] \boldsymbol{A}=\left[\begin{array}{cc}2 & 6 \\6 & 20\end{array}\right] A=[26620]为正定矩阵, x T A x = 2 x 1 2 + 12 x 1 x 2 + 20 x 2 2 > 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=2 x_{1}{ }^{2}+12 x_{1} x_{2}+20 x_{2}{ }^{2}>0(\mathbf{x}\neq 0) xTAx=2x12+12x1x2+20x22>0(x=0),其图像最小值点为原点
- A = [ 2 6 6 18 ] \boldsymbol{A}=\left[\begin{array}{cc}2 & 6 \\6 & 18\end{array}\right] A=[26618]为半正定矩阵, x T A x = 2 x 1 2 + 12 x 1 x 2 + 18 x 2 2 ≥ 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=2 x_{1}{ }^{2}+12 x_{1} x_{2}+18 x_{2}{ }^{2}\geq0(\mathbf{x}\neq 0) xTAx=2x12+12x1x2+18x22≥0(x=0)
图像中,不只原点处函数值为0,例如当 x = [ x 1 x 2 ] = [ 3 − 1 ] \mathbf{x} =\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right]=\left[\begin{array}{l}3\\-1\end{array}\right] x=[x1x2]=[3−1]时,同样有 x T A x = 0 \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=0 xTAx=0
此时正好处在判定为正定矩阵的临界点上:
行列式为0、特征值0和20,因而是奇异矩阵、只有一个主元;
半正定矩阵所有特征值 ≥ 0 \geq 0 ≥0,而不像正定矩阵(所有特征值 > 0 >0 >0);- A = [ 2 6 6 7 ] \boldsymbol{A}=\left[\begin{array}{cc}2 & 6 \\6 & 7\end{array}\right] A=[2667]为不定矩阵, x T A x = 2 x 1 2 + 12 x 1 x 2 + 7 x 2 2 \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=2 x_{1}{ }^{2}+12 x_{1} x_{2}+7 x_{2}{ }^{2} xTAx=2x12+12x1x2+7x22
无法保证 x T A x ≥ 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}\geq0(\mathbf{x}\neq 0) xTAx≥0(x=0)或 x T A x ≤ 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}\leq0(\mathbf{x}\neq 0) xTAx≤0(x=0),故称“不定”;
图像上没有最小值点,只有一个原点处的鞍点
可以发现,从二次型 x T A x \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} xTAx的式子来看,是否为正定的,关键在于 x 1 x 2 x_{1} x_{2} x1x2前面的系数
( x 1 2 x_{1}{ }^{2} x12和 x 2 2 x_{2}{ }^{2} x22项必然非负,它们如果能完全“抵消” x 1 x 2 x_{1} x_{2} x1x2的影响,就是正定矩阵)
正定矩阵的几何意义
对于正交矩阵只要 x ≠ 0 \mathbf{x}\neq 0 x=0,二次型 x T A x > 0 \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0 xTAx>0,几何意义就是, x = 0 \mathbf{x}= 0 x=0就是该空间曲面的极小值点;
二元函数有严格局部极小值的条件是:
- 微积分视角:一阶导数为0,并且 f x x f y y > f x y 2 f_{x x} f_{y y}>f_{x y}^{2} fxxfyy>fxy2 ⇒ \Rightarrow ⇒极小值点
或者等价的表述为:
二元函数有极小值的条件是,一阶导数为0,并且二阶导数矩阵 [ f x x f x y f y x f y y ] {\left[\begin{array}{ll}f_{x x} & f_{x y} \\f_{y x} & f_{y y}\end{array}\right]} [fxxfyxfxyfyy]为正定的;
其中, [ f x x f x y f y x f y y ] {\left[\begin{array}{ll}f_{x x} & f_{x y} \\f_{y x} & f_{y y}\end{array}\right]} [fxxfyxfxyfyy]称为Hessian矩阵,它是多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率,注意Hessian矩阵必然是对称矩阵,因为二阶偏导满足 f x y = f y x f_{x y}=f_{y x} fxy=fyx
在这个视角下,上述的 f x x f y y > f x y 2 f_{x x} f_{y y}>f_{x y}^{2} fxxfyy>fxy2实际上就是Hessian矩阵的行列式
- 线性代数视角:矩阵 A \boldsymbol{A} A正定 ⇒ \Rightarrow ⇒ x = 0 \mathbf{x}= 0 x=0就是 x T A x \mathbf{x}^{T} \boldsymbol{A} \mathbf{x} xTAx的极小值点
从上可见,正定矩阵的一个实际应用,就是最优化、主成分分析,详见二次型与正定矩阵
半正定、负定矩阵
- 正定Positive definite,
x
T
A
x
>
0
(
x
≠
0
)
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0(\mathbf{x}\neq 0)
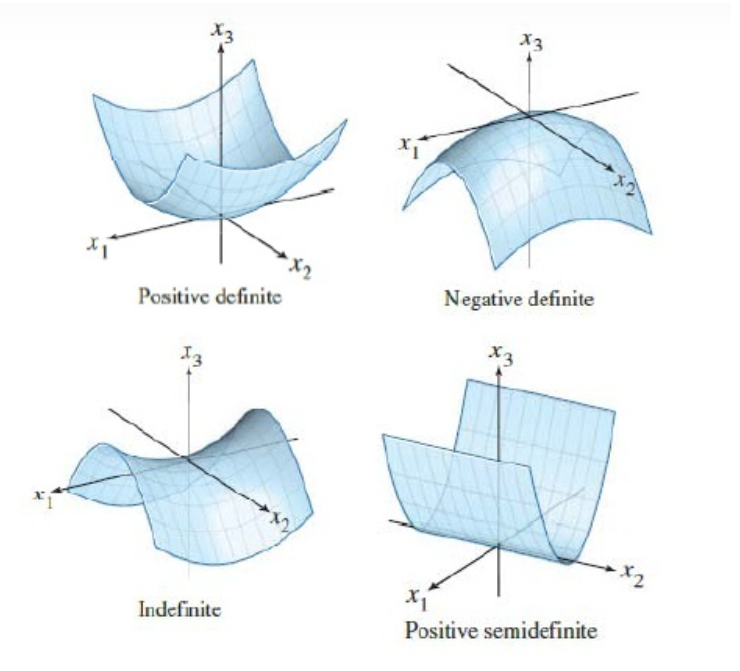
xTAx>0(x=0),对应的曲面为一个碗/抛物面,固定
z
z
z轴截取一个平面,得到椭圆
整个曲面可以找到极小值点 - 半正定Positive semidefinite ,
x
T
A
x
≥
0
(
x
≠
0
)
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}\geq 0(\mathbf{x}\neq 0)
xTAx≥0(x=0),对应的曲面为一个卷曲的纸面
注意,如果撇去半正定矩阵中“可归为正定”的那一部分正定矩阵,剩余的半正定矩阵满足 x T A x = 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=0(\mathbf{x}\neq 0) xTAx=0(x=0)
当半正定矩阵满足 x T A x = 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=0(\mathbf{x}\neq 0) xTAx=0(x=0)时,至少有一个特征值为0,则行列式为0,此时半正定矩阵为不可逆/奇异矩阵; - 负定Negative definite, x T A x < 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}<0(\mathbf{x}\neq 0) xTAx<0(x=0),对应的曲面为一个倒扣的碗
- 不定Indefinite,既不是半正定也不是半负定,对应的曲面为一个马鞍面,固定
z
z
z轴截取一个平面,得到双曲线
曲面没有极小值点,只有一个鞍点,鞍点在某个方向上看是极大值点,在另一方向上是极小值点,实际上最佳观测角度是特征向量的方向
正定矩阵与消元法、配方法的联系
给出二次型
x
T
A
x
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}
xTAx,如何判断对应的图像取值的正负呢?
可以用配方法,并且配方法中的各个系数来自于消元
例如,给出
A
=
[
2
6
6
20
]
\boldsymbol{A}=\left[\begin{array}{cc}2 & 6 \\6 & 20\end{array}\right]
A=[26620],
x
T
A
x
=
2
x
1
2
+
12
x
1
x
2
+
20
x
2
2
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=2 x_{1}{ }^{2}+12 x_{1} x_{2}+20 x_{2}{ }^{2}
xTAx=2x12+12x1x2+20x22,希望估计其图像(从而可以验证它是否有最小值、鞍点等,并且能进一步对应于正定/不定矩阵)
配方法:
f
(
x
,
y
)
=
2
x
2
+
12
x
y
+
20
y
2
=
2
(
x
+
3
y
)
2
+
2
y
2
f(x, y)=2 x^{2}+12 x y+20 y^{2}=2(x+3 y)^{2}+2 y^{2}
f(x,y)=2x2+12xy+20y2=2(x+3y)2+2y2可见,此时二次型
x
T
A
x
>
0
(
x
≠
0
)
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0(\mathbf{x}\neq 0)
xTAx>0(x=0),原点为最小值点,
A
\boldsymbol{A}
A为正定矩阵
配方法是高斯消元法中将式子表示为平方项的好方法,实际上,配方法就是在消元
从
[
2
6
6
20
]
\left[\begin{array}{cc}2 & 6 \\6 & 20\end{array}\right]
[26620]消元得到
[
2
6
0
2
]
\left[\begin{array}{cc}2 & 6 \\0 & 2\end{array}\right]
[2062],表示为LU分解,得到
配方就是将多项式写为完全平方项之和,其中:
- 平方项里面是消元的倍数因子
- 平方项外面的系数就是主元
这就是为什么消元后主元为正,则矩阵为正定矩阵(主元=完全平方项的系数,主元全为正,必然有 x T A x > 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0(\mathbf{x}\neq 0) xTAx>0(x=0),从而对应正定矩阵)
上面通过二次型表达式的配方的例子,说明了对于二元多项式的配方等价于二阶方阵的消元;
实际上可以推广:n元(二次)多项式的配方,等价于n阶矩阵的消元
推广:三阶方阵的二次型
给出 A = [ 2 − 1 0 − 1 2 − 1 0 − 1 2 ] \boldsymbol{A}=\left[\begin{array}{rrr}2 & -1 & 0 \\-1 & 2 & -1 \\0 & -1 & 2 \end{array}\right] A= 2−10−12−10−12 ,这是正定矩阵:
- 从左上角开始,子矩阵的行列式分别为2,3,4
- 消元后,对角线上的主元分别为 2 , 3 2 , 4 3 2,\frac{3}{2},\frac{4}{3} 2,23,34(计算技巧:利用行列式的特点,消元后对角线上的主元乘积等于行列式)
- 特征值为 2 − 2 , 2 , 2 + 2 2-\sqrt 2,2,2+\sqrt 2 2−2,2,2+2
- 二次型
x
T
A
x
=
2
x
1
2
+
2
x
2
2
+
2
x
3
2
−
2
x
1
x
2
−
2
x
2
x
3
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=2 x_{1}^{2}+2 x_{2}^{2}+2 x_{3}^{2}-2 x_{1} x_{2}-2 x_{2} x_{3}
xTAx=2x12+2x22+2x32−2x1x2−2x2x3
LU消元得到 [ 2 − 1 0 − 1 2 − 1 0 − 1 2 ] = [ 1 0 0 − 1 / 2 1 0 0 − 2 / 3 1 ] [ 2 − 1 0 0 3 / 2 − 1 0 0 4 / 3 ] \left[\begin{array}{rrr}2 & -1 & 0 \\-1 & 2 & -1 \\0 & -1 & 2 \end{array}\right]= \left[\begin{array}{rrr}1 & 0 & 0 \\-1/2 & 1 & 0 \\0 & -2/3 & 1 \end{array}\right] \left[\begin{array}{rrr}2 & -1 & 0 \\0 & 3/2 & -1 \\0 & 0 & 4/3 \end{array}\right] 2−10−12−10−12 = 1−1/2001−2/3001 200−13/200−14/3
对于配方法 2 x 1 2 + 2 x 2 2 + 2 x 3 2 − 2 x 1 x 2 − 2 x 2 x 3 = 2 ( x 1 − 1 / 2 x 2 ) 2 + 3 / 2 ( x 2 − 2 / 3 x 3 ) 2 + 4 / 3 ( x 3 ) 2 2 x_{1}^{2}+2 x_{2}^{2}+2 x_{3}^{2}-2 x_{1} x_{2}-2 x_{2} x_{3}\\=2(x_1-1/2x_2)^2+3/2(x_2-2/3x_3)^2+4/3(x_3)^2 2x12+2x22+2x32−2x1x2−2x2x3=2(x1−1/2x2)2+3/2(x2−2/3x3)2+4/3(x3)2可见有 x T A x > 0 ( x ≠ 0 ) \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}>0(\mathbf{x}\neq 0) xTAx>0(x=0),图像为碗/抛物面,有最小值点 - 此时二次型
x
T
A
x
\mathbf{x}^{T} \boldsymbol{A} \mathbf{x}
xTAx有三个变量,对应图像位于四维空间,若将函数值固定为1,“截取”图像,得到一个橄榄球 / 椭球体的方程
2
x
1
2
+
2
x
2
2
+
2
x
3
2
−
2
x
1
x
2
−
2
x
2
x
3
=
1
2 x_{1}^{2}+2 x_{2}^{2}+2 x_{3}^{2}-2 x_{1} x_{2}-2 x_{2} x_{3}=1
2x12+2x22+2x32−2x1x2−2x2x3=1
(类比:对于2阶正定矩阵,在高为1的位置截取,得到一个椭圆的方程)
从几何上, x T A x = 1 \mathbf{x}^{T} \boldsymbol{A} \mathbf{x}=1 xTAx=1的椭球体有三个主要的轴,三个轴的方向就是特征向量的方向,轴的长度就是特征值(由于有两根轴长度相等,对应于有一个二重特征值),这就是主轴定理 A = Q Λ Q T \boldsymbol{A}=\boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{T} A=QΛQT的几何解释(对称矩阵的对角化,得到两边为正交矩阵,故可用转置代替求逆,中间为特征值矩阵)
最小二乘法与半正定矩阵 A T A \mathbf A^T \mathbf A ATA
之前说过,根据最小二乘法, A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b无解时,转而求解 A T A x ^ = A T b \mathbf A^T\mathbf A \hat{\boldsymbol x}=\mathbf A^T\boldsymbol b ATAx^=ATb,该方程的解 x ~ \tilde{\boldsymbol x} x~会是“最优解”
实际上,其理论依据就在于,当 A \mathbf A A列满秩 r = n r=n r=n时, A T A \mathbf A^T \mathbf A ATA为满秩的正定矩阵,进而可逆(后一个方程必有解)
- 其中, A T A \mathbf A^T \mathbf A ATA至少是半正定矩阵,即 x T ( A T A ) x ≥ 0 ( x ≠ 0 ) \mathbf{x}^{T} (\mathbf A^T \mathbf A)\mathbf{x}\geq0(\mathbf{x}\neq 0) xT(ATA)x≥0(x=0)
从直观上理解,既然 x T x = ∣ x ∣ 2 ≥ 0 \mathbf x^T \mathbf x=|\mathbf x|^2\geq 0 xTx=∣x∣2≥0对应向量自身的模长平方;
类比可得,方阵阵 A T A \mathbf A^T \mathbf A ATA也就应该有半正定性
- 证明
x
T
(
A
T
A
)
x
≥
0
(
x
≠
0
)
\mathbf{x}^{T} (\mathbf A^T \mathbf A)\mathbf{x}\geq0(\mathbf{x}\neq 0)
xT(ATA)x≥0(x=0):
x
T
(
A
T
A
)
x
=
(
A
x
)
T
A
x
=
∣
A
x
∣
2
(
向量模长的平方
)
≥
0
(
x
≠
0
)
\mathbf{x}^{T} (\mathbf A^T \mathbf A)\mathbf{x}=(\mathbf A\mathbf{x})^T\mathbf A\mathbf{x}=|\mathbf A\mathbf{x}|^2(向量模长的平方)\geq 0(\mathbf{x}\neq 0)
xT(ATA)x=(Ax)TAx=∣Ax∣2(向量模长的平方)≥0(x=0)仅当向量
A
x
=
0
(
x
≠
0
)
\mathbf A\mathbf{x}=0(\mathbf{x}\neq 0)
Ax=0(x=0),不等式式取等号
这就是说,对于任意的长方形矩阵 A \mathbf A A:
当 A \mathbf A A列不满秩 r < n r<n r<n时, A x = 0 ( x ≠ 0 ) \mathbf A\mathbf{x}=0(\mathbf{x}\neq 0) Ax=0(x=0)有非零解,故 x T ( A T A ) x ≥ 0 ( x ≠ 0 ) \mathbf{x}^{T} (\mathbf A^T \mathbf A)\mathbf{x}\geq 0(\mathbf{x}\neq 0) xT(ATA)x≥0(x=0), A T A \mathbf A^T \mathbf A ATA为半正定矩阵,且不可逆(至少有一个特征值为0、行列式为0)
当 A \mathbf A A列满秩 r = n r=n r=n时, A x = 0 ( x ≠ 0 ) \mathbf A\mathbf{x}=0(\mathbf{x}\neq 0) Ax=0(x=0)有唯一零解, x T ( A T A ) x > 0 ( x ≠ 0 ) \mathbf{x}^{T} (\mathbf A^T \mathbf A)\mathbf{x}>0(\mathbf{x}\neq 0) xT(ATA)x>0(x=0), A T A \mathbf A^T \mathbf A ATA为正定矩阵,且可逆
原因:列满秩 r = n r=n r=n时,零空间维度 n − r = 0 n-r=0 n−r=0,从而 A x = 0 \boldsymbol{A x}=0 Ax=0有唯一零解,或者说各个列向量线性无关
小结: A T A \mathbf A^T \mathbf A ATA必至少为半正定,若此基础上还满足 A \mathbf A A列满秩 r = n r=n r=n( A \boldsymbol A A零空间只有零向量),则 A T A \mathbf A^T \mathbf A ATA为正定
- 从 A T A \mathbf A^T \mathbf A ATA的正定(可逆)上来说,更能理解最小二乘法中 A T A x ^ = A T b \mathbf A^T\mathbf A \hat{\boldsymbol x}=\mathbf A^T\boldsymbol b ATAx^=ATb为何一定有解
- A T A \mathbf A^T \mathbf A ATA正定, 为计算带来了很多便利:消元时不用行交换、不用担心主元为负、易于计算等
reference:
MIT—线性代数笔记27 正定矩阵和最小值
特殊矩阵 (6):正定矩阵
二次型的应用:二次型与正定矩阵