BP 神经网络算法识别MNIST手写数字数据集
人工神经网络的基本原理
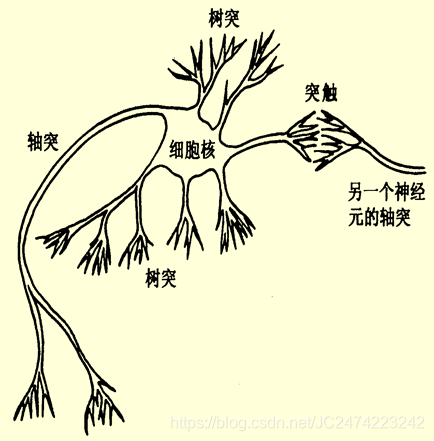
生物神经元在结构上由:
- 细胞体(Cell body)
- 树突(Dendrite)
- 轴突(Axon)
- 突触(Synapse)
四部分组成。用来完成神经元间信息的接收、传递和处理。
神经元及其突触是神经网络的基本器件。因此,模拟生物神经网络应首先模拟生物神经元, 人工神经元(节点)从三个方面进行模拟:
- 节点本身的信息处理能力
- 节点与节点之间连接(拓扑结构)
- 相互连接的强度(通过学习来调整)
神经元模型
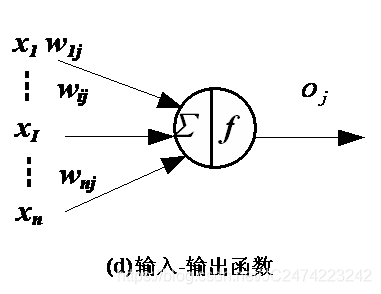
一般地,将形式神经元模型表示为下图所示的一个具有多输入-单输出的非线性阈值器件。
x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn表示某一神经元的第n个输入; W i j W_{ij} Wij表示第 i i i个神经元与第 j j j个神经元的突触连接强度,其称为权值。神经元模型将这些输入加权后经激励函数 f f f输出。
A j = ∑ j = 1 n x i W i j − Θ j A_j = \sum_{j=1}^nx_iW_{ij} - \Theta_j Aj=j=1∑nxiWij−Θj
O j = f ( A j ) O_j = f(A_j) Oj=f(Aj)
几个常见的神经元模型
- 阈值型
该类型的神经元具有一个设定的阈值,是一种最简单的神经元,当加权后的输入大于阈值时,输出为1,否则为0。
激励函数一般表示为:
y i = f ( A i ) = { 1 , A i > Θ i 0 , A i ≤ Θ i y_i = f(A_i) = \begin{cases} 1, \quad A_i \gt \Theta_i \\\\ 0, \quad A_i \leq \Theta_i \end{cases} yi=f(Ai)=⎩⎪⎨⎪⎧1,Ai>Θi0,Ai≤Θi
对于阈值型神经元, 其输入权值 W i j W_{ij} Wij可在 ( − 1 , + 1 ) (-1, +1) (−1,+1)区间连续取值。负值表示抑制,正值表示加强。 - 线性饱和型
线性饱和型神经元在一定区间内,输入输出满足线性关系。激励函数为:
y i = f ( A i ) = { 0 , A i < 0 C A i , 0 ≤ A i ≤ A c 1 , A i > A c y_i = f(A_i) = \begin{cases} 0, \quad A_i \lt 0 \\\\ CA_i, \quad 0 \leq A_i \leq A_c \\\\ 1, \quad A_i \gt A_c \end{cases} yi=f(Ai)=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧0,Ai<0CAi,0≤Ai≤Ac1,Ai>Ac
C C C为常量 - S(sigmoid)型
S型神经元是一类连续型神经元模型,采用S型函数(sigmoid 函数)。其激励函数为:
y i = f ( A i ) = 1 / ( 1 + e A i ) y_i = f(A_i) = 1/(1+ e^{A_i}) yi=f(Ai)=1/(1+eAi)
或
y i = f ( A i