完全二叉树

1、定义

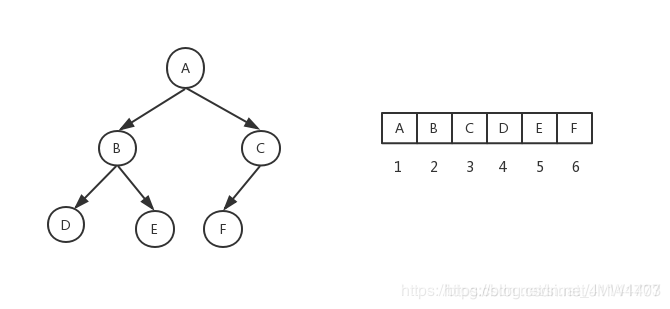
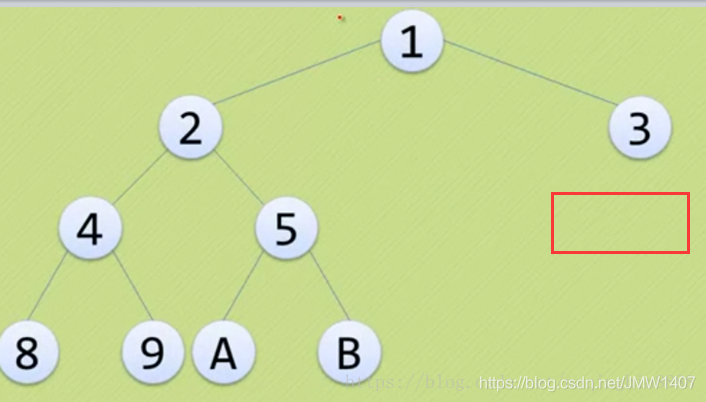
完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

• 若一棵二叉树至多只有最下面两层的结点的度数可以小于2，并且最下层的结点都集中在该层最左边的若干位置上，则此二叉树为完全二叉树。

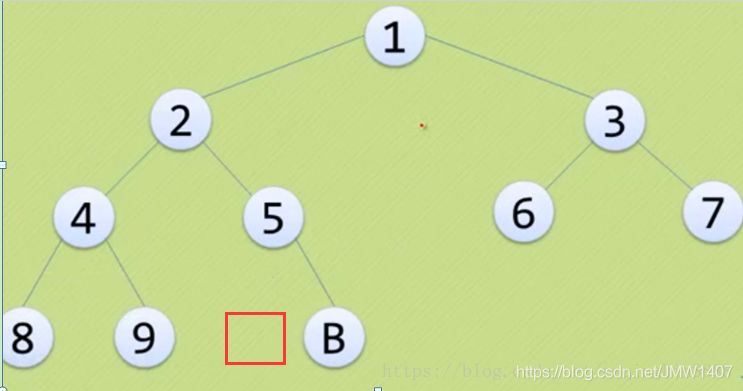
以下都不是完全二叉树

2、特征

叶子结点只可能在最下面的两层上出现，对任意结点，若其右分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L或L+1；

出于简便起见，完全二叉树通常采用数组而不是链表存储，其存储结构如下:

var tree : array[1...n] of object; {n:integer; n>=1}

对于tree，有如下特点：

（1）若i为奇数且i>1，那么tree[i]的左兄弟为tree[i-1]；

（2）若i为偶数且i<n，那么tree[i]的右兄弟为tree[i+1]；

（3）若i>1，tree[i]的双亲为tree[i div 2]；

（4）若2*i<=n，那么tree[i]的左孩子为tree[2*i]；若2*i+1<=n，那么tree[i]的右孩子为tree[2*i+1]；

（5）若i>n/2，那么tree[i]为叶子结点（对应于（3））；

（6）若i<(n-1)/2，那么tree必有两个孩子（对应于（4））；

（7）满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树；

（8）完全二叉树第i层至多有2^(i-1)个节点，共i层的完全二叉树最多有2^i-1个节点。

完全二叉树叶子结点数的算法

可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数：

由二叉树的性质可知：n0=n2+1，而n=n0+n1+n2（其中n为完全二叉树的结点总数）

由上述公式把n2消去得：n=2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，

由此得到n0=(n+1)/2或n0=n/2，就可根据完全二叉树的结点总数计算出叶子结点数。

具有n个结点的完全二叉树的深度为floor(log2n)+1或ceil(log2(n+1))

证明：设所求完全二叉树的深度为k。

由完全二叉树定义可得：

• 1、深度为k可以得到：完全二叉树的前k-1层是深度为k-1的满二叉树，一共有2^(k-1)-1个结点。
• 2、由于完全二叉树深度为k，故第k层上还有若干个结点，因此该完全二叉树的结点个数：n>2^(k-1)-1。
• 3、由二叉树的性质可知：n≤2^(k)-1，即：2^(k-1)-1<n≤2^k-1
• 4、由此可推出：2^(k-1)<≤n≤2k，取对数后有：k-1<log2n≤k

由于k-1和k是相邻的两个整数，故有k-1=floor(log2n)，由此即得：k=floor(log2n)+1。

3、C++简单实现完全二叉树的节点个数

完全二叉树的节点个数

• 思路：满二叉树节点个数为2^n-1个
• （1）情况1、遍历此二叉树右子树的左边界，如果左边界到达二叉树的最后一层，则此二叉树的左子树是满的。节点个数为2^(n-1 ) +1，也就是左子树的节点个数加上当前节点的个数。
• （2）情况2、如果左边界没有到达最后一层，则右子树肯定是满的，只不过层数得减一。

#include <iostream>
#include <stack>

struct Node {
    int value;
    Node* left;
    Node* right;
    Node(int value):
        value(value), left(nullptr), right(nullptr) {}
};

void preOrderRecur(Node* head) {//前序遍历
    if (head == nullptr) {
        return;
    }
    std::cout << head->value << ",";
    preOrderRecur(head->left);
    preOrderRecur(head->right);
}

int getMostLevel(Node* node, int curlevel) {//得到最左子树的深度
    while (node != nullptr) {
        curlevel++;
        node = node->left;
    }
    return curlevel - 1;//这里表达的意思，减1，应该就是把根节点对应的层数减掉，
    //下面的程序有补充加上根节点数量的过程。
}

//node当前节点，curlevel代表在第几层，depth二叉树的最大深度
int cbtNode(Node* node, int curlevel, int depth) {
    if (curlevel == depth) {//相当于只有根节点一个
        return 1;
    }
    if (getMostLevel(node->right, curlevel + 1) == depth) {//情况1
    //整体是以node为头的二叉树的节点个数。这里的curlevel + 1已经把node对应的节点层数加上去了。
        return (1 << (depth - curlevel)) + cbtNode(node->right, curlevel + 1, depth);
    } else {//情况2
        return (1 << (depth - curlevel - 1)) + cbtNode(node->left, curlevel + 1, depth);
    }

}
int cbtTotalNode(Node* head) {
    if (head == nullptr) {
        return 0;
    }
    return cbtNode(head, 1, getMostLevel(head, 1));
}

int main() {
    Node* head = new Node(1);
    head->left = new Node(2);
    head->right = new Node(3);
    head->left->left = new Node(4);
    head->left->right = new Node(5);
    head->right->left = new Node(6);

    std::cout << "==============recursive==============";
    std::cout << "\npre-order: ";
    preOrderRecur(head);
    std::cout << "\n";
    int cbt_total_nodes = cbtTotalNode(head);
    std::cout << cbt_total_nodes << std::endl;
    return 0;
}