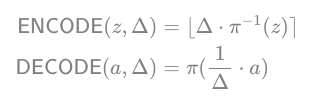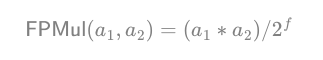本文主要为翻译内容,原文地址:https://www.inferati.com/blog/fhe-schemes-ckks
CKKS算法是2017年论文《Homomorphic Encryption for Arithmetic of Approximate Numbers》中提出的近似计算同态加密算法,论文的作者是Cheon等四位韩国研究者。算法早期因论文首字母缩写,称作HEAAN算法,其首个C++实现的库也作同名。后来为了加以区分,采用作者姓氏首字母,称为CKKS算法。
CKKS的核心是把加密噪声视为近似计算误差的一部分,也就是解密出来的结果直接视为原始消息的近似值。如果误差噪声相比消息来说足够小,那么噪声就不会破坏消息,在加密之前,将消息乘以一个缩放因子扩大消息,这样就可以减少添加噪声带来的误差。由此,消息+噪声可以用来替代原消息。
当然,CKKS还使用了重线性化和重缩放技术来减小密文计算时的扩张问题(有点像BV11、BGV、BFV结合的思想)让密文规模呈线性增长而不是指数级以增大乘法次数,还能顺带消除LSB位上的噪声。
1、介绍
CKKS,一种近似数字算术同态加密,又名HEAAN(Homomorphic Encryption for Arithmetic of Approximate Numbers),旨在为实数提供同态计算。其主要思想是将噪声(也称为误差 e)视为我们要加密的消息 μ(这里我们称为有效载荷)的一部分,噪声是出于安全目的在基于环学习错误(Ring-LWE)的全同态加密方案中引入的。有效载荷和噪声相结合生成我们要加密的明文。
因此,加密过程将作为输入,对我们的有效载荷的近似值进行加密,并生成一个密文。其背后的原理是,如果噪声的量级与有效载荷相比低得多,那么它可能对有效载荷或对有效载荷进行计算的结果没有明显影响。实际上,即使在不考虑加密的正常情况下,计算机也使用定点或浮点表示来处理实际数据。一些实际数据无法使用这些系统精确表示,我们所能做的就是通过标准截断或舍入程序以预定义的精度对其进行近似。这种近似会导致误差,这些误差在计算过程中会累积和扩大。但对于大多数实际情况,误差并不显著,因此最终结果是令人满意的。因此,我们可以将加密域中的
RLWE 误差视为明文域中的截断或舍入误差。
与其他全同态加密方案类似,在 CKKS 中,当我们对密文进行计算时,明文(包括有效载荷和误差)的量级会增长。如果我们将两个密文相加,增长是有限的,但如果我们将它们相乘,增长会更高。举个例子,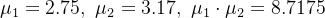
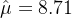
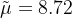
在明文域中,缩小规模是一个简单的过程,但在加密域中通常非常昂贵。早期的解决方案建议将舍入函数近似为一个多项式,以便提取和去除加密值的低位数字[HS15, CH18]。我们知道全同态加密非常适合在加密数据上计算多项式,这使得这种方法合理且易于实现。不幸的是,由于这些多项式的次数很高,这种方法在计算上很昂贵,在一般场景下可能不实用。然而,在 CKKS 之后,这一切完全改变了。
CKKS 方案的核心是一种称为 RESCALE 的机制,该机制用于减小明文(有效载荷和噪声)的量级。这个过程可以非常高效地模拟截断过程。CKKS引入了众所周知的全同态加密过程的MODSWITCH技术(modulus switching的缩写,模数转换),正如我们在前一篇文章【Introduction to the BGV encryption scheme】中所描述的,它主要在 BGV 方案中使用,以此来实现这种重新缩放的功能。事实上,人们很快就会注意到这两个方案之间的巨大相似性。
CKKS 解密以足够的精度生成有效载荷的近似值。只有当误差的大小远小于有效载荷的大小时,这才是可以接受的。幸运的是,通常情况下是这样的 —— 鉴于该方案被合理地参数化 —— 因为如后文所述,噪声是可以被控制的。
CKKS 重缩放提供了一种自然的方式来对加密实数进行计算,这与其他对整数进行计算全同态加密方案(如 FV [FV12]或BGV[BGV14])不同。应该指出的是,可以使用 BFV 和 BGV 对加密实数进行同态计算,但这需要复杂(并且通常效率低下)的编码过程[CSVW16]。此外,在计算过程中对结果进行缩小相当困难。
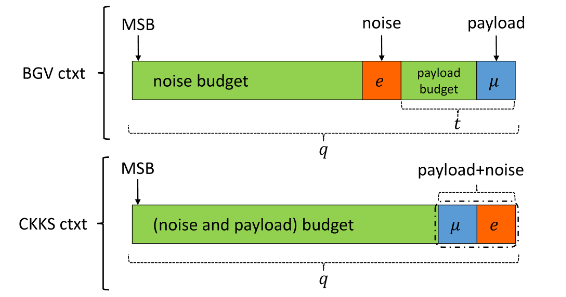
为了了解 CKKS 的工作原理,图 1 可能会有所帮助。该图展示了 BGV 和 CKKS 的密文结构。BGV 和 CKKS(甚至对于 BFV)中的密文通常是一对多项式。一个多项式包含有效载荷信息,而另一个用于解密。这些多项式的系数受整数q的限制,被称为密文系数模数,也就是说,它们可以取 0 到q-1之间的任何值。为了便于说明且不失一般性,假设这些多项式的次数为 0。在图 1 中,我们展示了 BGV 和 CKKS 方案中包含有效载荷信息的多项式密文结构。
BGV密文结构
首先,我们来研究 BGV 密文结构。记住这个类比并将密文想象成一个有界空间是很有用的。绿色区域是实体可能存在的开放空间。我们密文中的空间由 q 的值界定。有两个主要实体特别值得关注,即有效载荷 μ 和噪声 e。在 BGV 中,这两个组件是分开的,并且在计算的任何阶段都不应相互作用,否则有效载荷将丢失。这种分离只需在加密期间将噪声分量 e 按 t 进行缩放即可实现。这将如图 1(BGV ctxt)所示将误差向左移动 t。有效载荷可以在 t 界定的空间内自由移动,即取 0 到 t - 1之间的任何值。在同态计算过程中也应保持这一点。噪声分量 e 可以在 t 到q-1 的空间内自由移动(实际上小于这个范围,但为了使说明简单,我们不深入探讨细节)。只要误差或有效载荷位于它们各自的空间内,解密就有效,并且可以零精度损失地保留预期的有效载荷或计算结果。
CKKS密文结构
CKKS 方案中的密文结构略有不同。首先,两个主要成分 μ 和 e 组合形成一个单一实体。噪声是有效载荷的一部分。实际上,加密后无法将这两个成分(分离为它们的确切值)。这个更大的实体现在可以在 q 界定的空间中自由移动。人们可能会合理地怀疑,将 μ 和 e 组合可能会扭曲或损坏有效载荷,特别是如果有效载荷的量级很小(与 e 同阶)。这是一个合理的担忧,解决这个问题很简单,CKKS 通过一个参数(称为比例因子 ∆)来缩放有效载荷。这将把有效载荷的最高有效位向左移动,使其离 e 更远。假设 μ 的最低有效位在加上 e 后会被扭曲,但并不太重要,在实践中这确实是如此。为了帮助你理解为什么会这样,让我们来做下面的例子。
示例1.1:
设
,
且
。假设我们在缩放后使用截断来去除最低有效数字。
我们有
,这仍然是对缩放有效载荷的良好近似。
如果我们想要检索原始有效载荷,我们可以简单地除以比例因子。我们可以得到
,一般来说,这仍然是 π 的一个很好的近似值。如果我们使用更大的 ∆,我们可以得到一个更好的近似值。
在我们更深入地具体描述 CKKS 原语之前,复习一下定点算术会很有好处,因为 CKKS 所做的实际上是在加密域中模拟定点算术。我们请读者参考附录 A 以了解定点算术的概述。近似计算主要分为两类定点运算和浮点运算,区别在于缩放因子是否固定。CKKS方案采用的是定点运算,更加稳定(浮点运算很复杂,很难确定位的变化)。
2、明文和密文空间
在CKKS中,明文空间和密文空间几乎相同。它们包含多项式环![R_q =\mathbb Z_q[x]/f(x)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9SX3ElMjAlM0QlNUNtYXRoYmIlMjBaX3ElNUJ4JTVEL2YlMjh4JTI5)
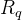
,其中n(称为环维度)是 2 的幂次方数。CKKS明文实例和密文实例之间的区别在于它们包含的环元素数量。一个CKKS明文实例包含一个环元素(多项式),而一个CKKS密文实例至少包含两个环元素。
上一段可能被认为与 CKKS 最初提出的目的相矛盾,即对加密实数进行计算,因为明文是具有整数系数的多项式。需要注意的关键思想是,CKKS 提出了新的编码和解码(编解码器)技术(稍后将进行描述),用于将实数向量(更准确地说是复数向量)映射到明文空间,反之亦然。正如我们之前提到的,CKKS 模拟定点算术运算,这些运算可以通过整数运算在整数操作数上完成。
3、明文编码和解码
CKKS 工作【CKKS17】的另一个主要贡献是一种新的编解码器方法,该方法将一个复数向量映射到单个明文对象,反之亦然。编码过程如下,给定一个长度为 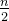
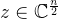
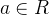

公式1:
现在应该很清楚 CKKS 编解码器方案与定点表示之间的联系。在我们对输入有效载荷进行编码时,会进行缩放。通过乘以 ∆ 完成,去除最低有效小数部分是通过四舍五入完成的。在解码中,我们逆转这个过程。在编码中乘以 ∆ 并四舍五入以及在解码中除以 ∆ 与我们在公式 15 中的定点编码所做的类似。
公式15:
4、参数
到目前为止,我们遇到了参数n,q 和 ∆。CKKS 在其实例化中使用了以下额外的特定于环学习错误(Ring-LWE)的分布:
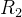
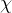
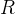
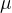
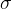
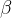
,参数
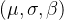
![(0,\frac{8}{\sqrt{2\pi}}\approx3.2,[6\cdot\sigma]=19)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjgwJTJDJTVDZnJhYyU3QjglN0QlN0IlNUNzcXJ0JTdCMiU1Q3BpJTdEJTdEJTVDYXBwcm94My4yJTJDJTVCNiU1Q2Nkb3QlNUNzaWdtYSU1RCUzRDE5JTI5)


关于参数 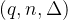
![[APS15]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJBUFMxNSU1RA%3D%3D)
我们注意到,与我们在第一篇文章中描述的 BFV 方案不同,CKKS 是一种尺度可变方案。这意味着在每个级别上,都有不同的系数模数。请记住,当我们执行同态乘法时,密文会按 ∆ 进行缩放。这会导致 q 的大小减小 ∆,我们最终会得到一个系数模数为 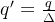
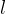
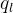
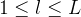
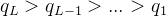
5、密钥生成
这个过程与 BFV 中的密钥生成过程非常相似。我们对秘密密钥 SK 进行采样,它是 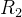
中。
公钥 PK 是一对多项式 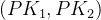
。
因此,a 是从
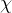
![[\cdot]_{q_{L}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlNUNjZG90JTVEXyU3QnFfJTdCTCU3RCU3RA%3D%3D)
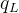
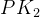
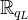
下进行。
6、加密与解密
为了在 R中加密一个明文消息 M(它是输入有效载荷向量的编码)。我们生成三个小的随机多项式,从 
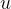
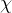
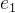
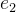

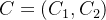
。
CKKS 中的加密与 BFV 中的加密的唯一区别在于我们不会用标量缩放 M。请注意,我们可以在任何级别 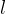
解密是通过在层级 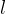
。
我们将解密为何有效的证明留作读者的练习。你可能想要回顾我们的 BFV 文章,以获得一些应对这一挑战的帮助。
7、同态计算
现在我们来描述在 CKKS 中同态操作是如何执行的。我们对两种操作感兴趣,即同态加法和同态乘法。前者与 BFV 非常相似。后者需要进行重缩放以保持计算精度不变。
EvalAdd
与 BFV EvalAdd 类似,我们只需将输入密文中的相应多项式相加,如下公式所示。请注意,假定输入密文处于同一层且具有相同的规模。如果情况并非如此,我们需要将较高层的密文缩小规模,以使其与另一个密文的规模和层相匹配。
EvalMult
同样,此过程与 BFV 中的 EvalMult 类似。推导也与我们在 BFV 中所做的类似,我们将其作为练习留给读者。我们仅展示如何在两个密文上计算 EvalMult,如下所示:
请注意, 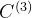
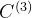

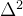
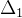
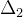

8、重新缩放
这个过程在我们第一篇文章【Introduction to the BFV encryption scheme】中讨论的尺度不变版本的 BFV 中并不存在。值得一提的是,BFV 也可以实例化为一个尺度可变方案。在这种情况下,可以使用一个称为 MODSWITCH 的过程在密文系数模数之间进行切换。CKKS 调整了 MODSWITCH 过程并将其称为 RESCALE。从数学上讲,它们是一样,但它们有两个不同的用途。在 CKKS 中使用它的主要目的通常是在乘法后减小比例因子,以与输入密文的比例因子相匹配。这个过程非常简单且计算效率高,它接受一个密文 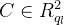
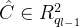
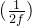
![RESCALE(C,\Delta)=\frac{1}{\Delta}\cdot[C_{1},C_{2}]_{q_{l}}=[\hat{C}]_{q_{l - 1}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9SESCALE%28C%2C%5CDelta%29%3D%5Cfrac%7B1%7D%7B%5CDelta%7D%5Ccdot%5BC_%7B1%7D%2CC_%7B2%7D%5D_%7Bq_%7Bl%7D%7D%3D%5B%5Chat%7BC%7D%5D_%7Bq_%7Bl%20-%201%7D%7D)
公式18:
9、乘法理解
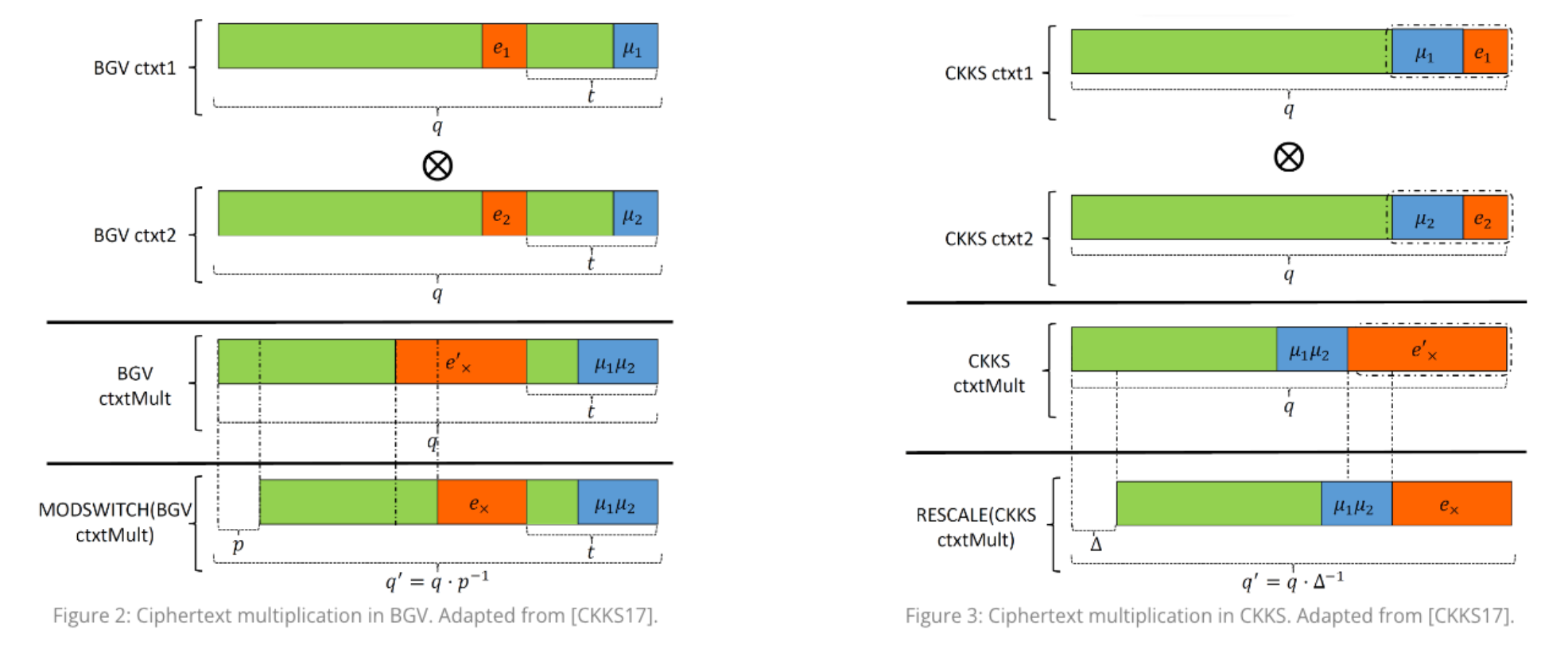
正如我们之前所说,CKKS 在密文域中模拟定点算术。图 2 和图 3 有助于理解这是如何实现的。首先,我们研究同态乘法在 BGV 中是如何工作的。同样,我们假设我们的密文有 2 个多项式,每个多项式都有一个系数。此外,我们只关注包含有效载荷的多项式。
如图 2 所示,乘法运算会使两个部分(有效载荷和噪声)的量级都增大。乘法结果包含在 t 所界定的空间,即在系数的低位比特中。乘积中的噪声也类似地增长,并从噪声预算中占用一些空间。如前所述,只要有效载荷和噪声是分开的,解密就能成功进行,并且可以无错误地检索有效载荷。为了对乘积密文结构有更多的直觉认识,让我们解下面这个代数方程:
为了减少乘法运算后噪声的增长,BGV 包含一种称为 MODSWITCH 的方法,该方法以加密明文 M且系数模数为 q的密文 C作为输入,并返回一个等效密文 C',它加密相同的明文,但具有不同的系数模数 q'。通常, 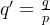
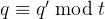
(11)
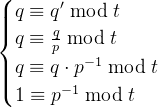
(12)
从上述推导中,很容易看出乘以 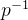
在 CKKS 中会发生稍微不同的情况。图 3 说明了 CKKS 同态乘法的内部工作原理。输入的明文,每个都包括有效载荷和噪声分量合并为一个块,进行相乘以生成因乘法误差而失真的有效载荷的乘积。我们可以像在 BGV 情况下那样推导出等式 13。

(13)
这几乎就是我们想要的结果,只是乘积的有效载荷被缩放了。为了使乘积保持与输入相同的比例因子,即 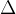
10、安全性
如我们之前所见,CKKS 与其他基于 RLWE 的全同态加密方案(特别是 BGV)有显著的相似之处。然而,在安全性方面,最近的一项工作[LM21]强调了一个重要的区别。一种有效的被动攻击被提出针对 CKKS。该攻击可以由具有以下能力的被动敌手(Eve)发起:
- 加密预言机这意味着 Eve 可以根据自己的意愿选择一些消息,并请求对其进行加密以生成有效的相应密文。这是一个非常合理的假设,因为全同态加密可以作为一种公钥加密方案进行部署,即加密密钥是公开可用的,任何人都可以访问它。即使全同态加密以私密模式部署,这仍然是一个合理的假设,并且它构成了一种常见攻击模型 —— 选择明文攻击下的不可区分性(IND-CPA)的基础。
- 能够选择将进行同态求值的函数。这也是一个合理的假设,因为 Eve 可能是负责执行外包同态计算的服务器本身。
- 解密预言机的访问权限:这意味着Eve可以选择一个密文并要求对其进行解密。这并不是一个非常牵强的假设,因为在计算后可能会共享解密结果。一些应用程序可能要求服务器知道某些解密后的值(由客户端在解密后以明文形式提供),以便继续进行应用程序。
具有上述特性的攻击模型现在被称为IND-CPA+ [LM21]。它可以被视为一种介于 IND-CPA 和 IND-CCA 之间的攻击模型。虽然 BFV 和 BGV 在 IND-CPA+ 下都是安全的,但普通的 CKKS 却不是。无需深入细节,这种攻击利用了 CKKS 中解密函数的线性性质以及近似解密结果提供了关于RLWE 错误的线索这一事实。通过简单的代数运算,在一次攻击尝试中(在最佳情况下)就可以恢复整个秘密密钥。这种攻击的计算需求是找到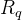
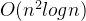
针对此漏洞,攻击的提出者建议通过在发布 CKKS 的解密结果之前向其添加额外的噪声来调整 CKKS 的解密函数【HElib库亦是通过修改解密函数来添加与密钥无关的噪声,以减轻这种攻击的风险】,以掩盖底层的 RLWE 噪声。一个开放的研究问题是如何找到添加噪声的严格界限,使得 CKKS 在 IND-CPA+ 下仍然安全,并且计算精度不受影响。
我们注意到,如果解密结果永远不会被发布或与不受信任的各方共享,那么仍然可以毫无顾虑地使用普通 CKKS,而不用担心其安全性问题。