文章收录于LeetCode专栏
盛最多水的容器
给你n个非负整数a1,a2,…,an,每个数代表坐标中的一个点(i, ai) 。在坐标内画 n 条垂直线,垂直线i的两个端点分别为(i, ai) 和 (i, 0)。找出其中的两条线,使得它们与x轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例 1:
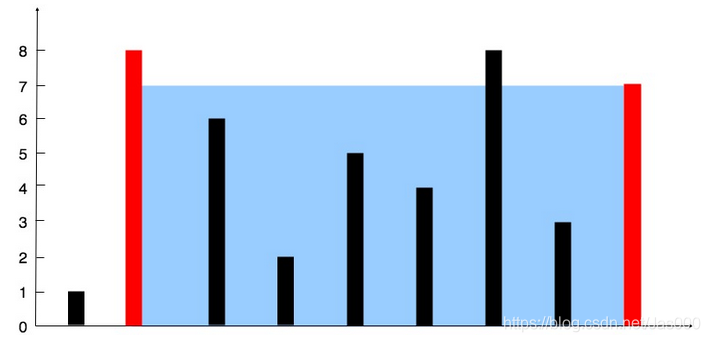
输入:[1, 8, 6, 2, 5, 4, 8, 3, 7]
输出:49
解释:图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为49
解题
1、审题
数组中各个元素表示柱子的高度(坐标系中的纵坐标),这里的高度就可以作为容器的高,两跟柱子之间的间距就作为容器的长,即容器最多容纳水就是高乘以长。要把柱子的高作为容器的高,就会必须得取二则的相对矮的那一根柱子。例如1和8之间就得取1。
2、列出所有解
通过对题意的理解可以使用暴力法和左右收敛法来解答改题目。
解法一(暴力法)
class Solution{
public int maxArea(int[] height){
int max = 0;
for(int i=0; i<height.length-1; i++){
for(int j=i+1; j<height.length; j++){
int area = Math.min(height[i], height[j]) * (j-i);
max = Math.max(max, area);
}
}
return max;
}
}
解法二(左右收敛)
class Solution{
public int maxArea(int[] height){
int max = 0;
for(int i=0, j=height.length-1; i<j;){
int h = height[i] < height[j] ? height[i++]:height[j--];
int area = h * (j-i+1);
max = Math.max(max, area);
}
return max;
}
}
3、复杂度分析
首先来看下暴力解法的时间复杂度和空间复杂度,因为暴力法使用了两层循环,所以时间复杂度为O(n2),没有使用任何额外空间,所以空间复杂度为O(1)。左右收敛法因为只使用一层循环,所以时间复杂度为O(n),同样空间复杂度为O(1)。综上左右收敛法是最优解。