前言 上一章中我们大致介绍了三维重建的背景、NeRF应用于三维重建的难点以及相关数据集和评估指标,本章节将会详细介绍NeRF原文以及部分源码,以及体渲染的物理模型,来帮助读者更好理解NeRF;下一章我们将会结合colmap,讲解部分nerf_pl源码,同时讲解一下cuda算子的使用。
本教程禁止转载。同时,本教程来自知识星球【CV技术指南】更多技术教程,可加入星球学习。
欢迎关注公众号CV技术指南,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读、CV招聘信息。
NeRF原文介绍
原文Nerf: Representing scenes as neural radiance fields for view synthesis发表于ECCV 2020
作者之一Ben Mildenhall,2020年毕业于UC Berkeley,截至2023年4/4就职于谷歌,并先后发表了Mip-NeRF,Block-NeRF,Mip-NeRP 360,DreamFUsion等众多堪称节点性的工作。
对于NeRF,我们在上一章中把它定义为可微渲染的一种方法,是为了强调其和几何重建算法的差别;现在我们不妨缩小一下定义范围,将它定义为神经渲染的一种方法,区别于传统可微渲染。
神经渲染通过使用深度神经网络近似场景参数(例如NeRF中的体密度,或是NeRF中第一个MLP网络输出的特征向量,这种表达我们称为神经表达),并通过训练神经网络来学习场景的光学性质,是一种数据驱动的渲染方法。
传统渲染想要生成真实场景的可控图像,需要从现有的观测(如图像和视频)中模拟光的传播规律来估计复杂的物理参数(例如相机内参、照明、反照率等),即逆渲染,从而生成真实感高的图像。
这个概念首次被提出来是在2018年的Neural scene representation and rendering中,想要深入学习的同学可以参考Advances in Neural Rendering。
但好消息是学习NeRF相比于学习图形学传统渲染或是学习传统三维重建来说,并不需要太多太深的基础知识,那么事不宜迟,我们尽快开始本章正式内容。
1.Introduction
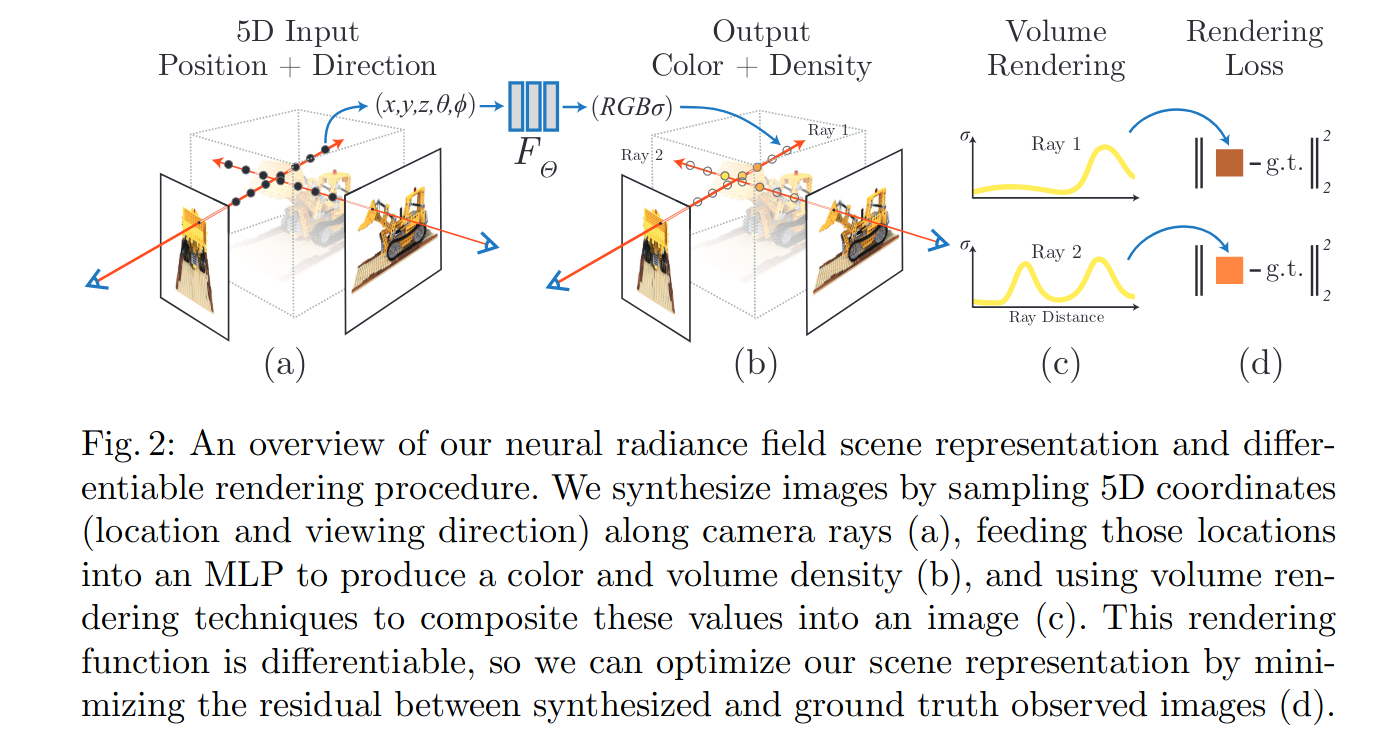
这一章中,Mildenhall概括介绍了他们整个工作的pipeline,具体为:
给定一系列带位姿的图片 I = I 1 , . . . , I n I={I_1,...,I_n} I=I1,...,In,以及对应的位姿 P = ( R 1 ∣ t 1 , . . . , R n ∣ t n ) P={(R_1|t_1,...,R_n|t_n)} P=(R1∣t1,...,Rn∣tn)与相机内参 K = ( K 1 , . . . , K n ) K=(K_1,...,K_n) K=(K1,...,Kn);在像素平面上采样点 ( u , v ) (u,v) (u,v),形成由相机光心 o − ( u , v ) o-(u,v) o−(u,v)的射线,并在射线上采样若干三维点 ( x , y , z ) (x,y,z) (x,y,z),在该射线上所有三维点的视线方向都可以表示为 ( d x ( u , v ) , d y ( u , v ) , d z ( u , v ) ) (d_{x}(u,v),d_{y}(u,v),d_{z}(u,v)) (dx(u,v),dy(u,v),dz(u,v))
a.用position encoding将低频的三维坐标映射到高频空间中以获取更细节的信息: γ p : = ( x , y , z ) → γ p ( x , y , z ) \gamma_p:=(x,y,z)\rightarrow \gamma_p(x,y,z) γp:=(x,y,z)→γp(x,y,z);
用MLP网络建立一个隐式表达映射 f g e o : = γ p ( x , y , z ) → ( σ , f ) f_{geo}:=\gamma_p(x,y,z)\rightarrow(\sigma,f) fgeo:=γp(x,y,z)→(σ,f),其中 σ \sigma σ表示体密度(volume density),控制通过 ( x , y , z ) (x,y,z) (x,y,z)的光线会累积多少辐射度/光强; f f f为该点的几何特征向量,隐式编码了 ( x , y , z ) (x,y,z) (x,y,z)的几何性质;
b.用position encoding将低频的方向向量映射到高频空间中以获取更细节的信息: γ d : = ( d x ( u , v ) , d y ( u , v ) , d z ( u , v ) ) → γ d ( d x ( u , v ) , d y ( u , v ) , d z ( u , v ) ) \gamma_d:=(d_x(u,v),d_y(u,v),d_z(u,v))\rightarrow \gamma_d(d_x(u,v),d_y(u,v),d_z(u,v)) γd:=(dx(u,v),dy(u,v),dz(u,v))→γd(dx(u,v),dy(u,v),dz(u,v));
用另一个MLP网络输出该点的RGB颜色 f c o l o r : = ( γ d ( d x ( u , v ) , d y ( u , v ) , d z ( u , v ) ) , f ) → c x , y , z f_{color}:=(\gamma_d(d_x(u,v),d_y(u,v),d_z(u,v)),f)\rightarrow c_{x,y,z} fcolor:=(γd(dx(u,v),dy(u,v),dz(u,v)),f)→cx,y,z;
c.使用传统体渲染方法,将这些三维点的颜色和密度累加到图像平面上;
*:使用 ( θ , ϕ ) (\theta,\phi) (θ,ϕ)来表示观察到该点的方向与使用__单位向量__ ( d x , d y , d z ) (d_x,d_y,d_z) (dx,dy,dz)是等价的,前者是采用经纬度表示,后者是采用单位向量表示,为了避免歧义,后面我们都以单位向量来表示方向,论文中提到的5D向量也都用6D向量说明。
*:整个NeRF模型的输入是一个6D向量 ( x i , y i , z i , d x i , d y i , d z i ) (x_i,y_i,z_i,d_{xi},d_{yi},d_{zi}) (xi,yi,zi,dxi,dyi,dzi),输出的是点 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)的颜色以及体密度 ( c i , σ i ) (c_i,\sigma_i) (ci,σi),可以看作是一个自回归模型。大概的流程如下图所示:
2.相关工作
2.1神经3D形状表达
这一部分介绍主要是介绍神经表达的相关方法:
神经表达的主要目的是将场景中的几何和光学特征转换成低维、可学习的特征表示,以方便神经网络学习和推断。然而用什么数据进行监督是一个问题,DeepSDF、Occupancy Networks、Local Deep Implicit Functions for 3D Shape和Local Implicit Grid Representations for 3D Scenes都需要三维数据进行监督,这些数据的真值在现实场景中是很难获取的。
在后续的一系列工作例如Differentiable Volumetric Rendering和Scene Representation Networks中允许仅用图像的RGB loss进行监督。
上述方法可以潜在地表示复杂和高分辨率的几何体,但它们仅能表达具有低几何复杂性的简单形状,从而导致渲染出的图像过度平滑。而NeRF通过将6D张量进行位置编码,使得网络能学习到更细节的几何、纹理信息,从而在渲染过程中有了更精细的画面。
2.2视图合成和基于图像的渲染
给定密集的视图采样,可以通过简单的光场采样插值技术重建逼真的新视图。对于具有稀疏视图采样的新视图合成,一类流行的方法是使用基于mesh的场景表示,然后使用可微光栅化来渲染图像,并用梯度下降来优化mesh的位置和材质。然而这类方法的优化通常很困难,并且与我们关注的体渲染技术不在一个频道上,我们可以跳过,想要了解这部分可微渲染知识的同学可以参考Differentiable Rendering: A Survey。
另一类较为流行的是采用体素表达场景,体素方法能够逼真地表示复杂的形状和材料,非常适合基于梯度的优化,并且往往比基于mesh的方法产生更少的视觉干扰伪影。早期的体素方法使用观察到的图像直接为体素网格着色;
后续的一些工作使用多个场景的大型数据集来训练深度网络,也即利用神经网络学习泛化的材质信息,这些网络从一组输入图像中预测采样体素,然后使用alpha合成或学习沿光线合成以在渲染时生成新视图;其他的一些工作针对一个特定场景优化了卷积网络和采样体素网格的组合,这样CNN可以补偿来自低分辨率体素网格的离散化伪影。
虽然这些体素方法在NVS取得了令人印象深刻的结果,但由于渲染更高分辨率的图像需要更精细的3D空间采样,它们扩展到更高分辨率图像的能力会因此收到限制。NERF通过在MLP的参数内编码场景信息来解决分辨率缺失的问题,这里我们可以理解为NeRF的输入是一个连续的空间,任意三维点都会有一个对应的体密度和颜色值,而不会受到网格分辨率的影响。
3.方法
3.1神经辐射场表达
给定一系列带位姿的图片 I = I 1 , . . . , I n I={I_1,...,I_n} I=I1,...,In,以及对应的位姿 P = ( R 1 ∣ t 1 , . . . , R n ∣ t n ) P={(R_1|t_1,...,R_n|t_n)} P=(R1∣t1,...,Rn∣tn)与相机内参 K = ( K 1 , . . . , K n ) K=(K_1,...,K_n) K=(K1,...,Kn);在像素平面上采样点 ( u , v ) (u,v) (u,v),形成由相机光心 o − ( u , v ) o-(u,v) o−(u,v)的射线,并在射线上采样若干三维点 ( x , y , z ) (x,y,z) (x,y,z),在该射线上所有三维点的视线方向都可以表示为 ( d x ( u , v ) , d y ( u , v ) , d z ( u , v ) ) (d_{x}(u,v),d_{y}(u,v),d_{z}(u,v)) (dx(u,v),dy(u,v),dz(u,v))
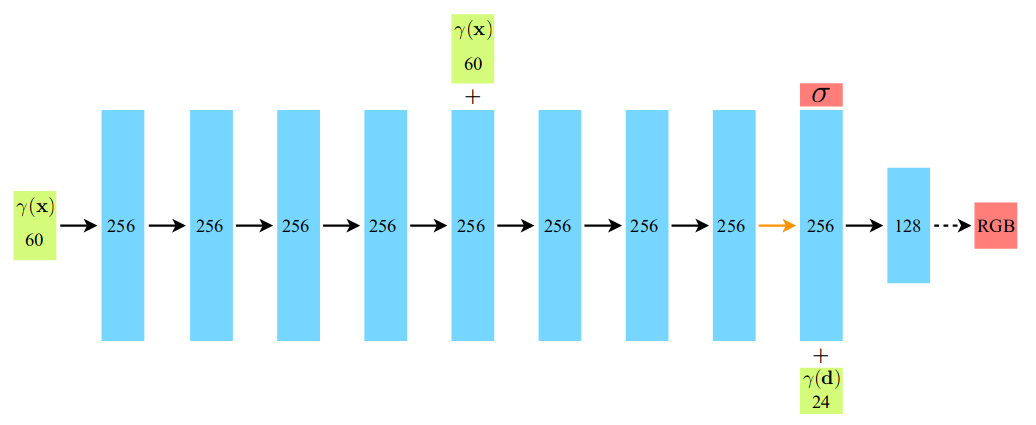
NeRF采用一个8层、256宽MLP网络用三维点空间位置坐标作为输入,预测该点的体密度和几何特征向量
f
g
e
o
:
=
(
x
,
y
,
z
)
→
(
σ
,
f
)
f_{geo}:=(x,y,z)\rightarrow(\sigma,f)
fgeo:=(x,y,z)→(σ,f)
其中
σ
\sigma
σ为该点体密度,其物理意义为射线在
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)处击中粒子的概率;
f
f
f为该点的几何特征向量。
并用另一个单层、256宽MLP用方向向量以及几何特征向量作为输入,预测该点的RGB颜色值:
f
c
o
l
o
r
:
=
(
d
x
(
u
,
v
)
,
d
y
(
u
,
v
)
,
d
z
(
u
,
v
)
,
f
)
→
c
x
,
y
,
z
f_{color}:=(d_x(u,v),d_y(u,v),d_z(u,v),f)\rightarrow c_{x,y,z}
fcolor:=(dx(u,v),dy(u,v),dz(u,v),f)→cx,y,z
*:
f
g
e
o
f_{geo}
fgeo在第四层加入了skip connection,也即将输入与第四层节点concat到一起再送入第五层MLP;网络结构可参照下一节的网络结构。
*: f g e o f_{geo} fgeo仅为三维点位置坐标的函数,是假设了__密度场__各向同性;而 f c o l o r f_{color} fcolor为几何特征向量与方向的函数是因为即使在同一三维空间点上,由于观察角度不同,材质等信息在RGB空间的表达也会不同,一个显而易见的例子是在镜面反射表面,不同的角度观察会观察到不同的颜色。事实上文章也说明了这一点:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-k2ivUSKM-1685695635216)(null)]
而NeRF之所以能合成新视图,除了其构建了一个密度场之外,还有一个原因是对方向 d d d做了插值。例如在上图中,两个视角观测到水面的颜色不同,若假设有一段从view 1渐渐过渡到view 2的连续帧,观测到水面该点的颜色也是会从view 1的颜色渐渐过渡到view 2的颜色,从这个角度,除非有特别复杂的非线性光照环境, f c o l o r f_{color} fcolor都不应该设置的过深。
3.2Positional Encoding(PE)
在On the Spectral Bias of Neural Networks的研究中(section 3)证明了深度神经网络会优先学习低频信息,这篇文章在用一个6层256宽的MLP网络去拟合一组傅里叶级数时,总是低频项先被回归,因此NeRF先采用了PE将低频的xyz坐标映射为一个包含高频信息的向量,再将该向量送入神经网络:
γ
(
p
)
=
(
s
i
n
(
2
0
π
p
)
,
c
o
s
(
2
0
π
p
)
,
.
.
.
,
s
i
n
(
2
L
−
1
π
p
)
,
c
o
s
(
2
L
−
1
π
p
)
)
\gamma(p)=(sin(2^0\pi p),cos(2^0\pi p),...,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))
γ(p)=(sin(20πp),cos(20πp),...,sin(2L−1πp),cos(2L−1πp))
*:
γ
\gamma
γ是对
(
x
,
y
,
z
,
d
x
,
d
y
,
d
z
)
(x,y,z,d_x,d_y,d_z)
(x,y,z,dx,dy,dz)的每一个元素都进行映射,其中在对位置进行映射时,
L
=
10
L=10
L=10,在对方向进行映射时,
L
=
4
L=4
L=4。因此一开始的xyz向量会变成60维向量,
(
d
x
,
d
y
,
d
z
)
(d_x,d_y,d_z)
(dx,dy,dz)会变成24维向量,如下图所示:
3.3应用于神经辐射场的体渲染技术
在传统体渲染方法中,假设场景存在若干粒子,光线在行进过程中会撞击这些粒子,从而损失/增加辐射量。当我们想要得到光线从物体表面发射到像素平面所呈现的颜色时,仅需要将所有撞击粒子所损失/增加的辐射量累加起来即可:
C
(
r
)
=
∫
t
n
t
f
T
(
t
)
σ
(
r
(
t
)
)
c
(
r
(
t
)
,
d
)
d
t
,
w
h
e
r
e
T
(
t
)
=
exp
(
−
∫
t
n
t
σ
(
r
(
s
)
)
d
s
)
(1)
C(r)=\int_{t_n}^{t_f}T(t)\sigma(r(t))c(r(t),d)dt,\; where\;T(t)=\exp(-\int_{t_n}^{t}\sigma(r(s))ds)\tag{1}
C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt,whereT(t)=exp(−∫tntσ(r(s))ds)(1)
其中
r
(
t
)
=
o
+
t
d
r(t)=o+td
r(t)=o+td表示从相机光心
o
o
o出发,沿方向
d
d
d行进的射线;
T
(
t
)
T(t)
T(t)表示光线从
t
n
t_n
tn行进至
t
t
t时的累积透射率,也即从
t
n
t_n
tn行进至
t
t
t未撞击任何粒子的概率。
在实际渲染时,我们采用数值积分的方式近似该积分:
C
^
(
r
)
=
∑
i
=
1
N
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
c
i
,
w
h
e
r
e
T
i
=
exp
(
−
∑
j
=
1
i
−
1
σ
j
δ
j
)
(2)
\hat{C}(r)=\sum_{i=1}^N{T_i(1-\exp(-\sigma_i\delta_i))c_i}, \;where\;T_i=\exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j)\tag{2}
C^(r)=i=1∑NTi(1−exp(−σiδi))ci,whereTi=exp(−j=1∑i−1σjδj)(2)
其中
δ
i
=
t
i
+
1
−
t
i
\delta_i=t_{i+1}-t_i
δi=ti+1−ti为两个采样点之间间距,同时我们可以用
α
i
=
1
−
exp
(
−
σ
i
δ
i
)
\alpha_i=1-\exp(-\sigma_i\delta_i)
αi=1−exp(−σiδi)来替换为传统渲染中的alpha值,也即不透明度,当alpha为1时,表示完全不透明;当alpha为0时,表示完全透明,这个值在某种意义上和体密度是等价的。
*:这里的体渲染公式和我们在传统体渲染方法所推导的形式略有不同,我们会在讲解完传统体渲染方法之后讨论。
3.4分层采样技术
考虑到在采样空间三维点进行体渲染的过程中,若每次训练都均匀在射线上采样会有一大部分点都落在自由空间区域,这对NeRF训练MLP网络是不利的。因此NeRF采用了一种分层采样策略,我们回顾一下公式 ( 2 ) (2) (2),该数值积分公式其实就是射线上每个采样点的加权和,其中权重为 ω i = T i ( 1 − exp ( − σ i δ i ) ) \omega_i=T_i(1-\exp(-\sigma_i\delta_i)) ωi=Ti(1−exp(−σiδi))。
那么在第一次采样中,我们在每条射线上均匀采样若干个点,就可以得到每个点的PDF值: ω ^ i = ω i / ∑ j = 1 N c ω j \hat{\omega}_i=\omega_i/\sum_{j=1}^{N_c}\omega_j ω^i=ωi/∑j=1Ncωj,权重高的点具有更高的体密度值,在下一次采样中,理应有更大的概率被选中,这样有利于我们快速跳过自由空间的采样点。
同时NeRF在两个采样过程中分别采用了不同的NeRF网络来采样,也即第一次前向过程使用一个粗糙网络,计算PDF值并得到新的采样点后,再送入一个精细网络渲染。在笔者看来,这样做的目的应该是为了更灵活地学习密度场分布。
*:虽然原始NeRF采用了两个网络来分开粗糙与精细采样的过程,但在后续的一些工作中,往往仅使用一个网络,而反复多次采样。
NeRF的原理介绍到此结束,因为本篇内容旨在介绍NeRF的原理与传统体渲染的联系,NeRF的实验与分析可以移步论文。
体渲染的物理模型
1.传统体渲染简介
可参考Volume Rendering Digest (for NeRF)、Physically Based Rendering与Octane Render渲染器
体渲染技术在图形学已经有比较长的历史了,在体渲染领域,假设场景由若干粒子组成,光线 p = o + t ω p=o+t\omega p=o+tω,从 t = 0 t=0 t=0处出发,沿 ω \omega ω方向碰到这些粒子会产生如下现象:
a.吸收:光线 L L L的的一部分能量被粒子吸收
b.外散射: L L L的一部分光线打在粒子上散射到其他方向上
c.自发光:光线 L L L吸收了粒子的一部分光能
d.内散射:其他方向的光打在粒子上恰好散射到光线 L L L的方向上
其中,吸收和外散射现象都会引起光强减弱,而自发光和内散射现象会引起光强增强。我们可以用线性微分方程表达这些过程:
a.对于吸收, d L ( p ( t ) ) = − σ a ( p ( t ) ) ∗ L ( p ( t ) ) ∗ d t dL(p(t))=-\sigma_a(p(t))*L(p(t))*dt dL(p(t))=−σa(p(t))∗L(p(t))∗dt,表示光线到达 p ( t ) p(t) p(t)处因吸收现象导致光强线性衰减;
b.对于外散射, d L ( p ( t ) ) = − σ s ( p ( t ) ) ∗ L ( p ( t ) ) ∗ d t dL(p(t))=-\sigma_s(p(t)) * L(p(t)) * dt dL(p(t))=−σs(p(t))∗L(p(t))∗dt,表示光线到达 p ( t ) p(t) p(t)处因外散射现象导致光强线性衰减;
c.对于自发光,光线 L L L强度随光程 d t dt dt增大,增量仅与发光粒子有关: d L ( p ( t ) ) = L e ( p ( t ) ) ∗ d t dL(p(t))=L_e(p(t)) * dt dL(p(t))=Le(p(t))∗dt
d.对于内散射,由于包含了多条其他方向的光打在粒子上散射后在 L L L方向上的分量,我们不妨先定义相位函数为 P ( ω i → ω ) P(\omega_i\rightarrow\omega) P(ωi→ω),意为一条从 ω i \omega_i ωi方向射入的光散射到 L L L方向 ω \omega ω的占比(概率密度),对应的光强为 L i L_i Li;则经过内散射后,光强增量可表示为: d L ( p ( t ) ) = ( σ s ( p ( t ) ) ∫ Ω P ( ω i → ω ) L i ( p ( t ) ) d ω i ) d t dL(p(t))=(\sigma_s(p(t))\int_\Omega P(\omega_i\rightarrow\omega)L_i(p(t))d\omega_i)dt dL(p(t))=(σs(p(t))∫ΩP(ωi→ω)Li(p(t))dωi)dt,其中 Ω \Omega Ω为球面
上面公式的 σ s ( p ( t ) \sigma_s(p(t) σs(p(t)和 σ a ( p ( t ) ) \sigma_a(p(t)) σa(p(t))分别表示光线在该粒子( t t t)处因外散射、吸收引起光强衰减的比例系数,由于__只有这两种现象__会引起光强减小,我们可以用一个总的衰减系数 σ t ( p ( t ) ) = σ a ( p ( t ) ) + σ s ( p ( t ) ) \sigma_t(p(t))=\sigma_a(p(t))+\sigma_s(p(t)) σt(p(t))=σa(p(t))+σs(p(t))表示;
这样我们可以解微分方程:
d
L
(
p
(
t
)
)
=
−
σ
t
(
p
(
t
)
)
L
(
p
(
t
)
)
d
t
dL(p(t))=-\sigma_t(p(t))L(p(t))dt
dL(p(t))=−σt(p(t))L(p(t))dt得到:
L
(
p
(
t
)
)
=
L
0
e
−
∫
0
t
σ
t
(
p
(
u
)
)
d
u
=
L
0
T
r
(
p
(
0
)
→
p
(
t
)
)
(3)
\begin{align} L(p(t))&=L_0e^{-\int_0^t\sigma_t(p(u))du}\\ &=L_0T_r(p(0)\rightarrow p(t)) \end{align}\tag{3}
L(p(t))=L0e−∫0tσt(p(u))du=L0Tr(p(0)→p(t))(3)
这就是著名的比尔定律:光在均匀介质中传播,光强呈指数衰减;这里我们可以对比一下NeRF中的消光系数/体密度
σ
\sigma
σ
同时
L
e
(
p
(
t
)
)
L_e(p(t))
Le(p(t))与
σ
s
(
t
)
∫
Ω
p
(
ω
i
→
ω
)
L
i
(
t
)
d
ω
i
\sigma_s(t)\int_\Omega p(\omega_i\rightarrow\omega)L_i(t)d\omega_i
σs(t)∫Ωp(ωi→ω)Li(t)dωi都与原始光强无关,我们可以用
S
(
p
(
t
)
)
S(p(t))
S(p(t))表示:
S
(
(
p
(
t
)
)
)
=
L
e
(
p
(
t
)
)
+
σ
s
(
p
(
t
)
)
∫
Ω
P
(
ω
i
→
ω
)
L
i
(
p
(
t
)
)
d
ω
i
S((p(t)))=L_e(p(t))+\sigma_s(p(t))\int_\Omega P(\omega_i\rightarrow\omega)L_i(p(t))d\omega_i
S((p(t)))=Le(p(t))+σs(p(t))∫ΩP(ωi→ω)Li(p(t))dωi
接下来我们将上述四种现象全合并到同一个公式中:
d
L
(
p
(
t
)
)
d
t
=
−
σ
t
(
p
(
t
)
)
L
(
p
(
t
)
)
+
S
(
p
(
t
)
)
(4)
\frac{dL(p(t))}{dt}=-\sigma_t(p(t))L(p(t))+S(p(t))\tag{4}
dtdL(p(t))=−σt(p(t))L(p(t))+S(p(t))(4)
公式
(
2
)
(2)
(2)是一个一阶线性非齐次微分方程,我们可以采用该类方程的通解公式直接写出
L
L
L的解来:
L
(
p
(
t
)
)
=
e
−
∫
0
t
σ
(
p
(
x
)
)
d
x
(
∫
0
t
S
(
p
(
x
)
)
e
∫
0
x
σ
(
p
(
u
)
)
d
u
d
x
+
C
)
L(p(t))=e^{-\int^t_0{\sigma(p(x))dx}}(\int_0^t{S(p(x))e^{\int_0^x{\sigma(p(u))du}}dx}+C)
L(p(t))=e−∫0tσ(p(x))dx(∫0tS(p(x))e∫0xσ(p(u))dudx+C)
将
L
(
t
=
0
)
=
L
0
L(t=0)=L_0
L(t=0)=L0初值代入可得到
C
=
L
0
C=L_0
C=L0
也即
L ( t ) = e − ∫ 0 t σ ( x ) d x ( ∫ 0 t S ( x ) e ∫ 0 x σ ( u ) d u d x + L 0 ) = ∫ 0 t S ( x ) e ∫ 0 x σ ( u ) d u − ∫ 0 t σ ( x ) d x d x + L 0 e − ∫ 0 t σ ( x ) d x = ∫ 0 t S ( x ) e − ∫ x t σ ( u ) d u d x + L 0 e − ∫ 0 t σ ( x ) d x (5) \begin{align} L(t)&=e^{-\int^t_0{\sigma(x)dx}}(\int_0^t{S(x)e^{\int_0^x{\sigma(u)du}}dx}+L_0)\\ &=\int_0^t{S(x)e^{\int_0^x{\sigma(u)du}-\int^t_0{\sigma(x)dx}}}dx+L_0e^{-\int^t_0{\sigma(x)dx}}\\ &=\int_0^t{S(x)e^{-\int_x^t{\sigma(u)du}}}dx+L_0e^{-\int^t_0{\sigma(x)dx}} \end{align}\tag{5} L(t)=e−∫0tσ(x)dx(∫0tS(x)e∫0xσ(u)dudx+L0)=∫0tS(x)e∫0xσ(u)du−∫0tσ(x)dxdx+L0e−∫0tσ(x)dx=∫0tS(x)e−∫xtσ(u)dudx+L0e−∫0tσ(x)dx(5)
意为光线从 L ( t = 0 ) = L 0 L(t=0)=L_0 L(t=0)=L0出发,撞击若干粒子到达 t t t处后的光强。
在传统体渲染/可微渲染中,我们通常会对上述现象的相关参数(例如反照率,反射率)进行显式建模,根据不同的假设分为BSDF场、BRDF场等等。而NeRF作为一种神经渲染方法,与它们最大的区别就是NeRF不依靠光学模型,而是用MLP对__神经辐射场__重建,用神经网络进行隐式表达;同时由于辐射场的密度参数与传统体渲染的参数物理意义不同,其渲染公式也略有不同。
2.NeRF神经辐射场与体渲染物理模型的联系
NeRF这种隐式表达+体渲染的模式是不是横空出世的呢?其实不是,例如在NIPS 2019中也有这么一篇MLP隐式表达场景+体渲染的Oral工作Scene representation networks: Continuous 3d-structure-aware neural scene representations;
我们把这类用神经网络来编码渲染参数的方法统称为神经渲染(neural rendering)。但以往该类工作渲染的质量并没有NeRF如此惊艳,达到了photo-realistic级别的渲染。笔者认为NeRF主要的贡献有三点:
a.用MLP网络学习出了体密度,且该体密度具有的概率性质有利于后续的分层采样;
b.引入了Positional Encoding,将低频空间坐标映射到高频坐标;
c.体渲染公式的改进
NeRF的渲染公式
(
1
)
(1)
(1)与我们推导出的体渲染公式
(
5
)
(5)
(5)略有不同,原因在于NeRF的体密度
σ
\sigma
σ定义为:在光线行进无穷小距离时击中粒子的概率。回顾一下NeRF中透射率
T
(
t
)
T(t)
T(t)的定义为:从
t
n
t_n
tn行进至
t
t
t未撞击任何粒子的概率,则我们可以列出在光线行进了
T
+
d
t
T+dt
T+dt之后,未撞击粒子的概率是:
T
(
t
+
d
t
)
=
T
(
t
)
(
1
−
d
t
∗
σ
(
t
)
)
⇒
T
(
t
+
d
t
)
−
T
(
t
)
d
t
=
T
′
(
t
)
=
−
T
(
t
)
σ
(
t
)
T(t+dt)=T(t)(1-dt*\sigma(t))\\ \Rightarrow\frac{T(t+dt)-T(t)}{dt}=T'(t)=-T(t)\sigma(t)
T(t+dt)=T(t)(1−dt∗σ(t))⇒dtT(t+dt)−T(t)=T′(t)=−T(t)σ(t)
对于该微分方程我们同样可以给出通解:
T
(
a
→
b
)
=
T
(
b
)
T
(
a
)
=
exp
(
−
∫
a
b
σ
(
t
)
d
t
)
T(a\rightarrow b)=\frac{T(b)}{T(a)}=\exp(-\int^b_a{\sigma(t)dt})
T(a→b)=T(a)T(b)=exp(−∫abσ(t)dt)
同时,我们可以定义
O
(
0
→
t
)
=
1
−
T
(
0
→
t
)
O(0\rightarrow t)=1-T(0\rightarrow t)
O(0→t)=1−T(0→t)定义为射线在到达
t
t
t之前的某个时间确实击中粒子的概率,这是一个概率分布函数,其概率密度恰好等于
T
(
t
)
σ
(
t
)
T(t)\sigma(t)
T(t)σ(t),意为射线恰好停在
t
t
t的概率。
这样一来,NeRF的体渲染公式就等价于计算在射线上所有点颜色的期望值。
回顾公式 ( 5 ) (5) (5),这两个公式都满足在均匀介质中,光强/透射率呈指数衰减趋势,这也是NeRF将体渲染应用到其特有的体密度场的一个改进。本质上其是构建了一个概率场,而公式 ( 1 ) (1) (1)中的颜色也可以换成其他的物理量例如monosdf中将其替换为了法向量、深度。
预告
本章中,我们讲解了NeRF原文与传统体渲染方法,并探讨了他们之间的联系,下一张我们将会结合colmap,讲解部分源码,并讲解cuda算子的使用。
由于NeRF相关的框架太多了,适合初学者的有
原版NeRF(用tensorflow实现,与现在的NeRF开发环境不太一致)
nerf_pl(Ai葵用torchlightning实现的版本,有相关的YouTube教程,其后来实现的ngp_pl也是属于上手代码之一,只是torchlightning对初学者不太友好,学习周期可能会变长)
nerf_pytorch(mit大佬使用torch实现的版本,代码嵌套不深,比较易读)
考虑到后续内容大多会涉及torch lightning,我们选择nerf_pl进行部分源码解读
欢迎关注公众号CV技术指南,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读、CV招聘信息。
【技术文档】《从零搭建pytorch模型教程》122页PDF下载
QQ交流群:470899183。群内有大佬负责解答大家的日常学习、科研、代码问题。
模型部署交流群:732145323。用于计算机视觉方面的模型部署、高性能计算、优化加速、技术学习等方面的交流。
其它文章
ICLR 2023 | RevCol:可逆的多 column 网络,大模型架构设计新范式
CVPR 2023 | 即插即用的注意力模块 HAT: 激活更多有用的像素助力low-level任务显著涨点!
ICML 2023 | 轻量级视觉Transformer (ViT) 的预训练实践手册
即插即用系列 | 高效多尺度注意力模块EMA成为YOLOv5改进的小帮手
即插即用系列 | Meta 新作 MMViT: 基于交叉注意力机制的多尺度和多视角编码神经网络架构
全新YOLO模型YOLOCS来啦 | 面面俱到地改进YOLOv5的Backbone/Neck/Head
libtorch教程(一)开发环境搭建:VS+libtorch和Qt+libtorch