💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
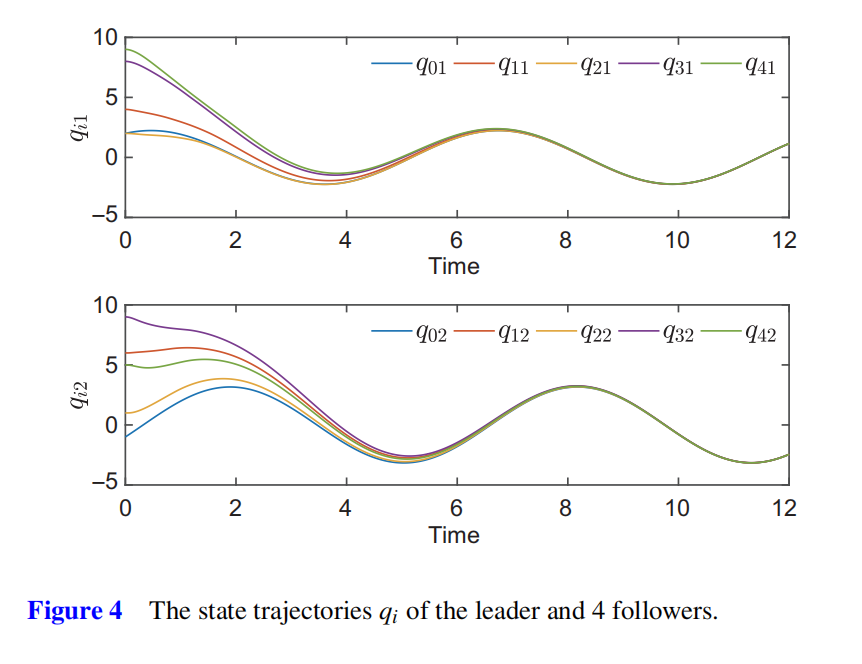
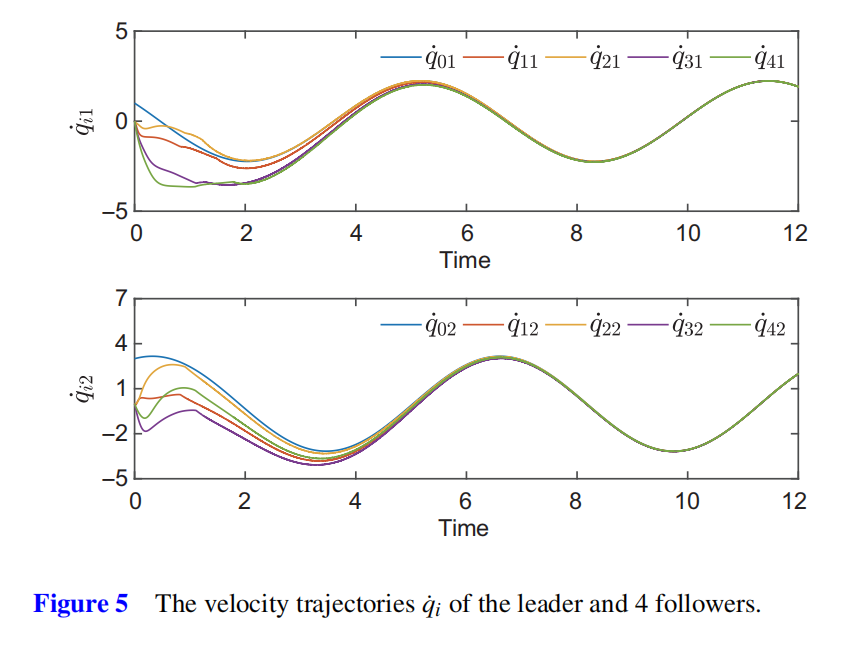
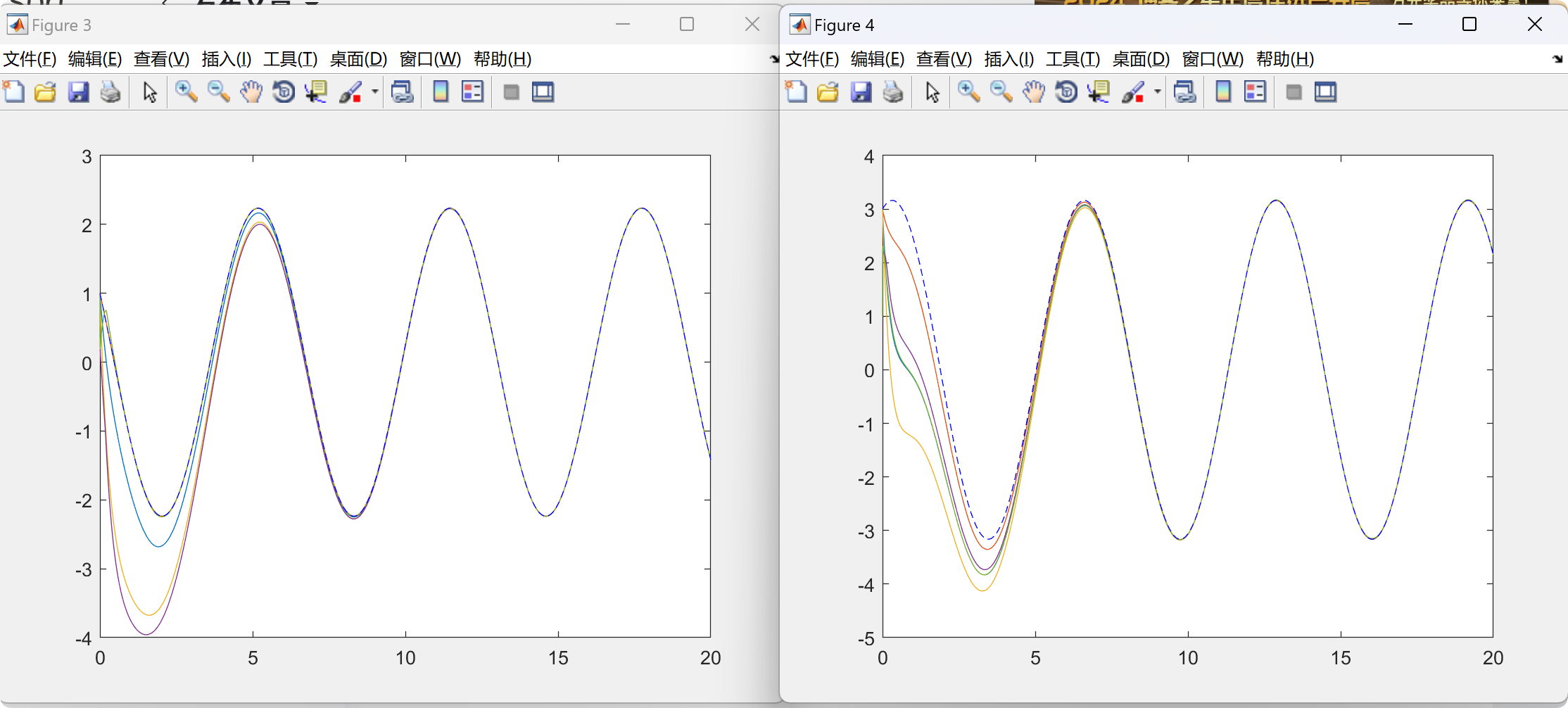
本文研究了一类受扰的网络化欧拉-拉格朗日系统,以在一般有向通信网络下跟踪一般虚拟信号。首先,构建了一类固定时间分布式观测器,用于估计领导者状态。其次,基于该分布式观测器,为每个跟随者提出了一种局部抗干扰跟踪控制策略,以在固定时间内实现跟踪一致性。最后,通过仿真实例验证了所提算法的有效性。
关键词:固定时间跟踪;网络化欧拉-拉格朗日系统;抗干扰控制;有向网络。
在过去的二十年中,多智能体系统的协同控制不仅引起了学术界的关注,也受到了工业界的重视,这主要归功于其在智能电网、无人机和多船只等众多领域的广泛应用以及由此引发的理论挑战。协同控制问题通常是指控制一群多智能体系统以实现一个共同目标。作为协同控制的一个基础研究课题,一致性问题近年来得到了广泛研究。一致性是指一群智能体通过局部交互对某些特定变量达成一致。一般来说,一致性问题可以分为三类:无领导者的一致性、有一个领导者的跟踪一致性以及有两个或更多领导者的包含控制。通常情况下,一群智能体需要被引导去跟随一个指定的智能体或预定义的虚拟信号,以完成特定任务。因此,本文作者主要关注跟踪一致性问题。评估一致性算法性能的一个关键指标是收敛速度。研究表明,一致性算法的收敛速度不仅取决于控制增益和动态特性,还取决于所有智能体之间的通信网络以及网络中智能体的数量。为了提高收敛速度,人们做出了大量努力,其中有限时间一致性算法是一个重要类别,因为在大多数实际应用中,一致性需要在有限时间内达成。然而,有限时间一致性算法的收敛时间(称为调整时间)通常明确依赖于初始状态信息,这限制了此类算法的应用,特别是在初始状态信息不可用的情况下。为了克服这种弱点,提出了固定时间稳定性的概念。从那时起,大量关于固定时间一致性的研究成果不断涌现。在文献[21]、[22]和[24]中考虑的动态模型是积分型模型,而在文献[23]中考虑的是一般线性模型。
结论
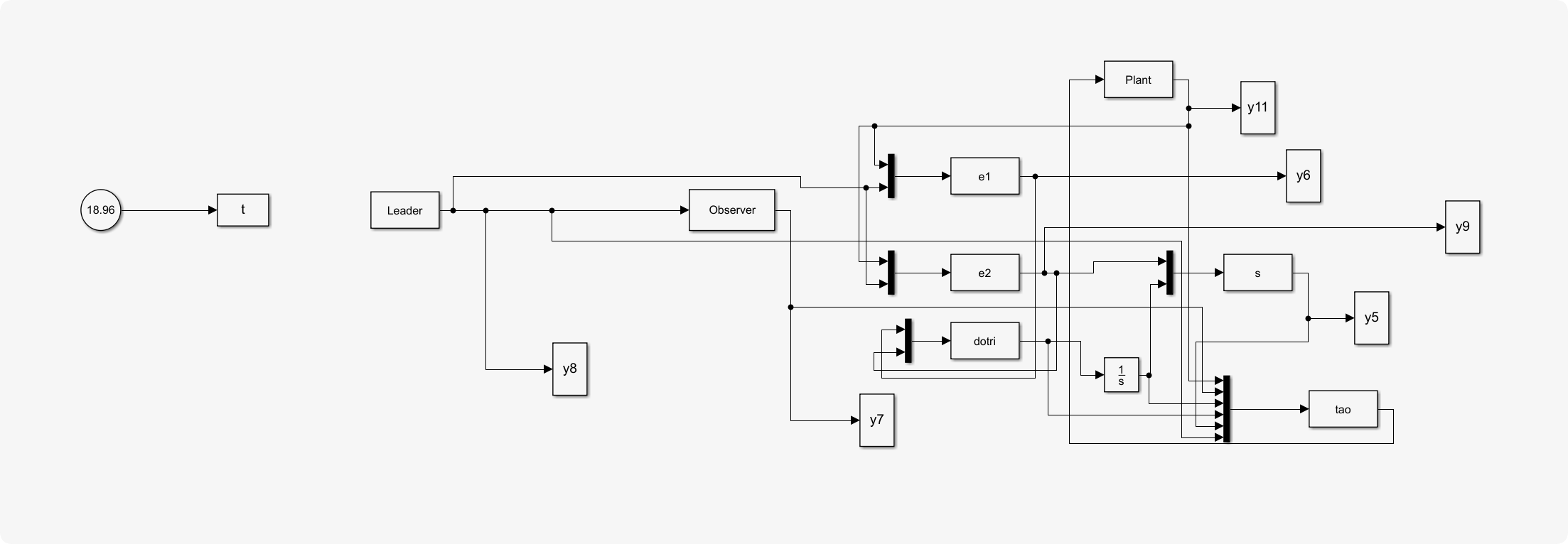
本文主要研究了网络化欧拉-拉格朗日系统的分布式跟踪一致性问题,其中领导者受到非线性动态的影响,而跟随者受到有界干扰的影响。首先,设计了一类分布式观测器,以在固定时间内协同估计非线性领导者的状态。然后,为每个跟随者构建了一种基于积分滑模的局部控制协议,以在固定时间内跟踪观测器。进一步的研究方向包括:针对时延网络化欧拉-拉格朗日系统的固定时间无领导者一致性问题,以及具有通用有向通信网络的网络化欧拉-拉格朗日系统的完全分布式固定时间一致性问题。
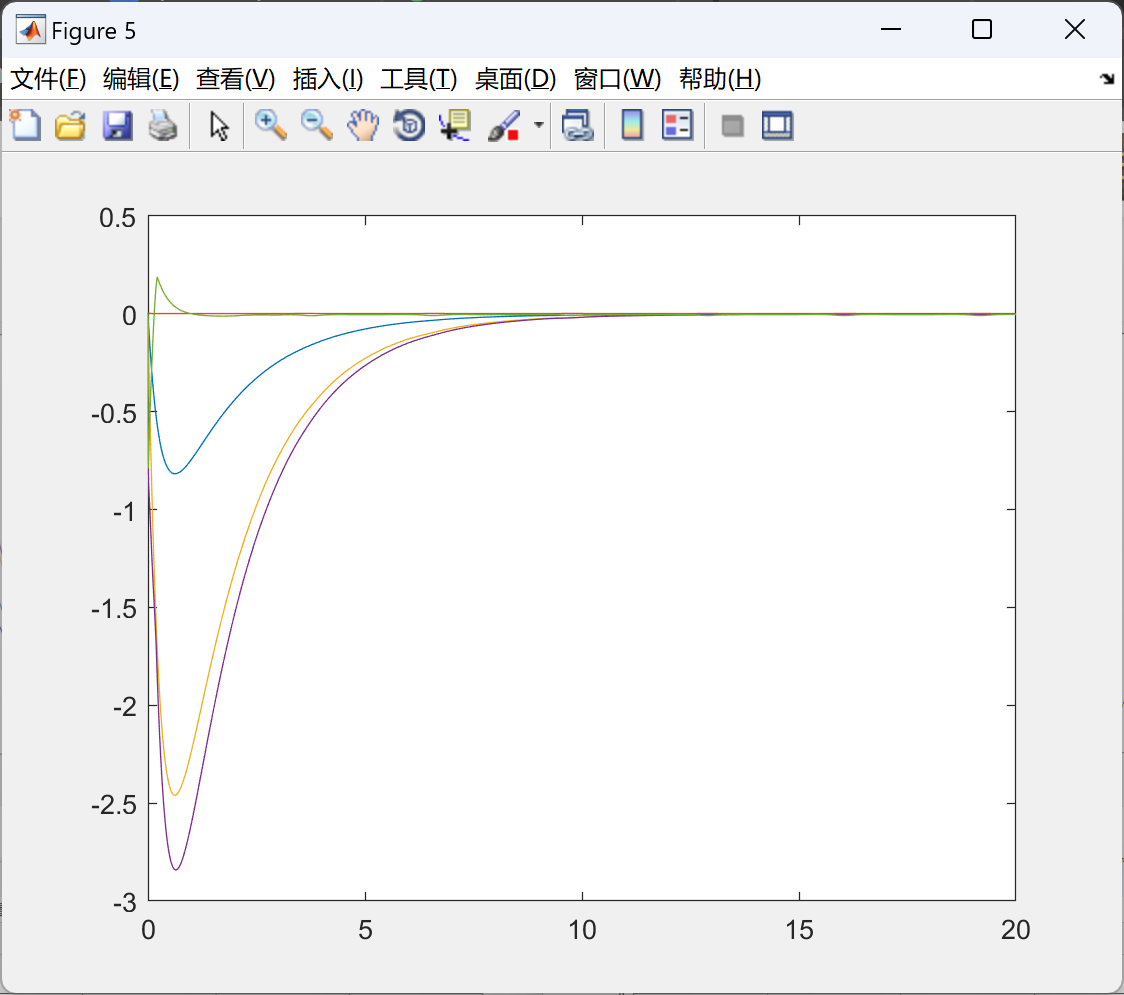
📚2 运行结果
部分代码:
M1=[m11+m12+2*m13*cos(q1_2) m12+m13*cos(q1_2);m12+m13*cos(q1_2) m12];
M2=[m21+m22+2*m23*cos(q2_2) m22+m23*cos(q2_2);m22+m23*cos(q2_2) m22];
M3=[m31+m32+2*m33*cos(q3_2) m32+m33*cos(q3_2);m32+m33*cos(q3_2) m32];
M4=[m41+m42+2*m43*cos(q4_2) m42+m43*cos(q4_2);m42+m43*cos(q4_2) m42];
M5=[m51+m52+2*m53*cos(q5_2) m52+m53*cos(q5_2);m52+m53*cos(q5_2) m52];
C1=-[m13*sin(q1_2)*dotq1_2 m13*sin(q1_2)*(dotq1_1+dotq1_2);-m13*sin(q1_2)*dotq1_1 0];
C2=-[m23*sin(q2_2)*dotq2_2 m23*sin(q2_2)*(dotq2_1+dotq2_2);-m23*sin(q2_2)*dotq2_1 0];
C3=-[m33*sin(q3_2)*dotq3_2 m33*sin(q3_2)*(dotq3_1+dotq3_2);-m33*sin(q3_2)*dotq3_1 0];
C4=-[m43*sin(q4_2)*dotq4_2 m43*sin(q4_2)*(dotq4_1+dotq4_2);-m43*sin(q4_2)*dotq4_1 0];
C5=-[m53*sin(q5_2)*dotq5_2 m53*sin(q5_2)*(dotq5_1+dotq5_2);-m53*sin(q5_2)*dotq5_1 0];
g=9.8;
G1=[m14*cos(q1_1)+m15*g*cos(q1_1+q1_2);m15*cos(q1_1+q1_2)];
G2=[m24*cos(q2_1)+m25*g*cos(q2_1+q2_2);m25*cos(q2_1+q2_2)];
G3=[m34*cos(q3_1)+m35*g*cos(q3_1+q3_2);m35*cos(q3_1+q3_2)];
G4=[m44*cos(q4_1)+m45*g*cos(q4_1+q4_2);m45*cos(q4_1+q4_2)];
G5=[m54*cos(q5_1)+m55*g*cos(q5_1+q5_2);m55*cos(q5_1+q5_2)];
tempt1=inv(M1)*(u1+d1-C1*[dotq1_1;dotq1_2]-G1);
tempt2=inv(M2)*(u2+d2-C2*[dotq2_1;dotq2_2]-G2);
tempt3=inv(M3)*(u3+d3-C3*[dotq3_1;dotq3_2]-G3);
tempt4=inv(M4)*(u4+d4-C4*[dotq4_1;dotq4_2]-G4);
tempt5=inv(M5)*(u5+d5-C5*[dotq5_1;dotq5_2]-G5);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
🌈4 Matlab代码、Simulink仿真、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取