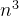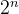方法调用的时间复杂度
int i, j;
for (i = 0; i < n; i++)
{
function(i);
}
上面这段代码调用一个函数function。
void function(int count)
{
print(count);
}
函数体是打印这个参数。其实这很好理解,function函数的时间复杂度是O(1)。所以整体的时间复杂度为O(n)。
假如function是下面这样的:
void function(int count)
{
int j;
for (j = count; j < n; j++)
{/* 时间复杂度为O(1)的程序步骤序列 */}
}
事实上,这和刚才举的例子是一样的,只不过把嵌套内循环放到了函数中,所以最终的时间复杂度为O(n2)。
下面这段相对复杂的语句:
n++; /* 执行次数为1 */
function(n); /* 执行次数为n */
int i, j;
for (i = 0; i < n; i++) /* 执行次数为n2*/
{
function (i);
}
for (i = 0; i < n; i++) /* 执行次数为n(n + 1)/2 */
{for (j = i; j < n; j++)
{/* 时间复杂度为O(1)的程序步骤序列 */}
}
它的执行次数f(n)=1+n+n2+n(n+1)/2=3/2·n²+3/2·n+1,根据推导大O阶的方法,最终这段代码的时间复杂度也是O(n2)。
| 执行次数 | 函数阶 | 非正式术语 |
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n²+2n+1 | O(n² ) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
6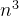 +2n² +3n+4 +2n² +3n+4 | O(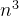 ) ) | 立方阶 |
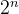 | O(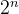 ) ) | 指数阶 |
常用的时间复杂度所耗费的时间从小到大依次是:
O(1)<O(logn)<O(n)<O(nlogn)<O(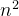
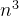
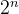
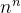
像O(