文章目录
1、李雅普诺夫稳定性 (Lyapunov Stable)
1.1 概念
是一种局部稳定性
这一部分是DR_CAN 【Advanced控制理论】6_稳定性_李雅普诺夫_Lyapunov学习笔记
李雅普诺夫稳定性定义:对于
∀
t
0
>
0
,
\forall t_0>0,
∀t0>0,
∀
ϵ
>
0
,
\forall\epsilon>0,
∀ϵ>0,
∃
δ
(
t
0
,
ϵ
)
\exists\delta(t_0,\epsilon)
∃δ(t0,ϵ), 满足
∥
x
(
t
0
)
∥
<
δ
(
t
0
,
ϵ
)
\lVert x(t_0)\rVert<\delta(t_0,\epsilon)
∥x(t0)∥<δ(t0,ϵ), 若对于
∀
t
>
t
0
\forall t>t_0
∀t>t0, 都存在
∥
x
(
t
)
∥
<
ϵ
\lVert x(t)\rVert<\epsilon
∥x(t)∥<ϵ, 则系统李雅普诺夫稳定。
汉译汉:如果平衡状态
x
e
x_e
xe受到扰动后,
t
0
t_0
t0时刻系统动态方程的解在
x
e
x_e
xe的
δ
\delta
δ邻域内,对
t
0
t_0
t0时刻之后的时间,系统动态方程的解在
x
e
x_e
xe的
ϵ
\epsilon
ϵ邻域内,我们就称
x
e
x_e
xe在李雅普诺夫意义下是稳定的。
特征值:所有特征值实部非正。
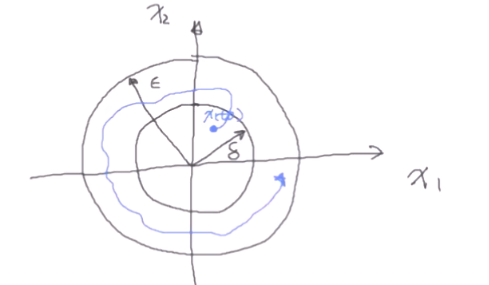
DR_CAN的讲解中,用下图直观地说明了它的性质。
1.2 解法
常用的是李雅普诺夫第二方法,即直接方法。
对于一个系统
x
˙
=
f
(
x
)
\dot x=f(x)
x˙=f(x), 其稳定点为
x
e
=
0
x_e=0
xe=0 。若存在
V
(
x
)
V(x)
V(x),满足
(
1
)
V
(
0
)
=
0
(
2
)
V
(
x
)
≥
0
,
V
(
x
)
P
S
D
i
n
D
−
{
0
}
(
3
)
V
˙
(
x
)
≤
0
,
V
˙
(
x
)
N
S
D
i
n
D
−
{
0
}
(1) V(0)=0\\ (2) V(x)≥0,V(x)\ PSD \ in \ D-\{0\}\\ (3) \dot V(x)≤0,\dot V(x)\ NSD\ in \ D-\{0\}
(1)V(0)=0(2)V(x)≥0,V(x) PSD in D−{0}(3)V˙(x)≤0,V˙(x) NSD in D−{0}
则系统李雅普诺夫稳定。
PSD:Positive Semi Definite 半正定
NSD:Negative Semi Definite 半负定
2、渐进稳定性 (Asympototically Stable)
2.1 概念
渐进稳定性定义:对
∃
δ
(
t
0
)
>
0
\exists\delta(t_0)>0
∃δ(t0)>0, 当
x
(
t
0
)
x(t_0)
x(t0)满足
∥
x
(
t
0
)
∥
<
δ
(
t
0
)
\lVert x(t_0)\rVert<\delta(t_0)
∥x(t0)∥<δ(t0)时,有
lim
t
→
∞
\lim\limits_{t\to \infty}
t→∞lim
∥
x
(
t
)
∥
=
0
\lVert x(t)\rVert=0
∥x(t)∥=0,系统渐进稳定。
特征值:所有特征值实部为负。
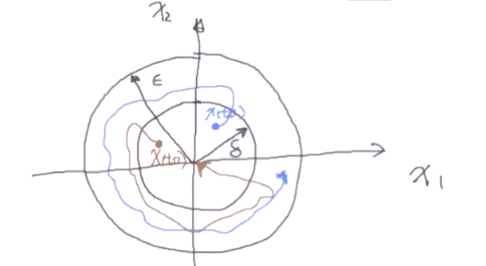
DR_CAN的讲解中,用下图红色线直观地说明了它的性质。
2.2 解法
对于一个系统
x
˙
=
f
(
x
)
\dot x=f(x)
x˙=f(x), 其稳定点为
x
e
=
0
x_e=0
xe=0 。若存在
V
(
x
)
V(x)
V(x),满足
(
1
)
V
(
0
)
=
0
(
2
)
V
(
x
)
>
0
,
V
(
x
)
P
D
i
n
D
−
{
0
}
(
3
)
V
˙
(
x
)
<
0
,
V
˙
(
x
)
N
D
i
n
D
−
{
0
}
(1) V(0)=0\\ (2) V(x)>0,V(x)\ PD \ in \ D-\{0\}\\ (3) \dot V(x)<0,\dot V(x)\ ND\ in \ D-\{0\}
(1)V(0)=0(2)V(x)>0,V(x) PD in D−{0}(3)V˙(x)<0,V˙(x) ND in D−{0}
则系统渐进稳定。
难点是找
V
(
x
)
V(x)
V(x)。
3、指数稳定性 (Exponentially Stable)
指数稳定:如果系统平衡状态 x e x_e xe是渐近稳定的,且状态轨迹收敛到平衡点的速度大于等于某个关于 t t t的指数函数,则称平衡状态 x e x_e xe是指数稳定的。