【C++复习】经典笔试题

文章目录

八大排序
- 快排过程
卡特兰数
反转链表
链表的回文结构
左叶子之和
另一棵树的子树
归并排序
类与对象
编程训练

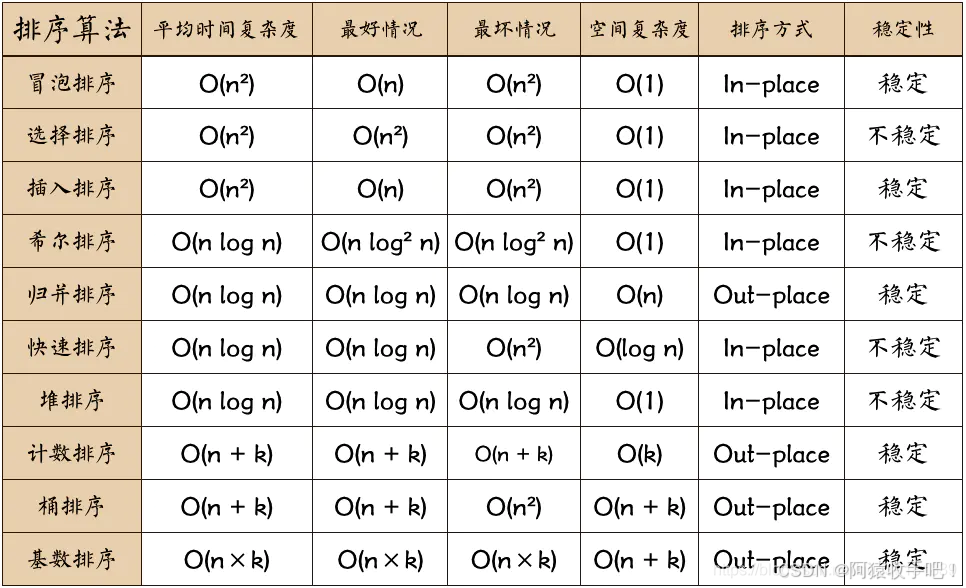
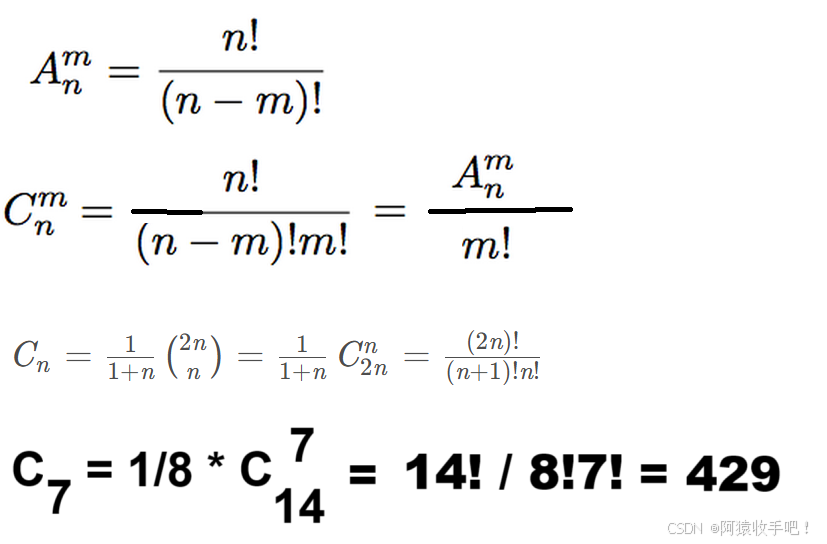八大排序

插冒归稳定

在这里插入图片描述

快排过程

以 [3,4,6,1,2,4,7] 为例，以第一个元素3为base，定义左右两个指针（小熊l，小熊r），分别从两端开始扫描。从右向左找比3小的数，替换l所在位置的元素。再从左往右找比3大的数，然后替换r所在位置的元素。重复此过程直至两个小熊重合（两个指针指向同一元素），base替换此元素，此时第一轮结束。再递归排序base左右两部分的元素。

卡特兰数

在这里插入图片描述

C0 = 1,         
C1 = 1,         C2 = 2,          C3 = 5,          C4 = 14,          C5 = 42,
C6 = 132,       C7 = 429,        C8 = 1430,       C9 = 4862,        C10 = 16796,
C11 = 58786,    C12 = 208012,    C13 = 742900,    C14 = 2674440,    C15 = 9694845,
C16 = 35357670, C17 = 129644790, C18 = 477638700, C19 = 1767263190, C20 = 6564120420, ...

反转链表

💡 采用翻指针法，将每个节点的next指针翻转一下，让其指向前一个节点即可

struct ListNode* ReverseList(struct ListNode* head )
{
    struct ListNode* prev=NULL;//prev指针初始为为NULL，考虑链表本身为空的情况
    struct ListNode* cur=head;
    while(cur)
    {
        struct ListNode* next=cur->next;//先保存下一个节点，防止下面翻指针过程中丢失next节点
        cur->next=prev;
        prev=cur;
        cur=next;
    }
    return prev;//prev最终指向原链表最后一个节点，即翻转后的第一个节点
}

💡 头插法，遍历原链表每个节点，将其头插到初始为NULL的新链表上即可

struct ListNode* ReverseList(struct ListNode* head )
{
    struct ListNode* cur=NULL;//cur指针初始化为NULL，考虑链表本身为空的情况
    while(head)
    {
        struct ListNode* next=head->next;//先保存下一个节点，防止下面翻指针过程中丢失next节点
        //头插
        head->next=cur;
        cur=head;
        head=next;
    }
    return cur;//cur最终指向原链表最后一个节点，即翻转后的第一个节点
}

💡 递归法，先递归到最后链表的最后一个节点处，然后在回退的时候进行翻指针

struct ListNode* ReverseList(struct ListNode* head ) 
{
    if(head==NULL||head->next==NULL)
    { 
        return head; 
    }
    struct ListNode* cur = ReverseList(head->next);// 这里的cur就是最后一个节点
    head->next->next = head;
    // 防止链表循环，需要将head.next设置为空
    head->next = NULL;
    // 每层递归函数都返回cur，也就是最后一个节点
    return cur;//这里就是将最后一个节点不断返回回去
}

💡 三指针法，就是用三个指针定位三个节点，做到翻指针的效果

struct ListNode *ReverseList(struct ListNode *head)
{
    if (head == NULL)
    {
        return NULL;
    }
    struct ListNode *prv = NULL, *cur = head, *nxt = cur->next;
    while (cur)
    {
        cur->next = prv;
        prv = cur;
        cur = nxt;

        if (nxt)
            nxt = nxt->next;
    }
    return prv;
}

链表的回文结构

先通过快慢指针的方式，找到链表中间节点。
再将后半部分链表进行反转。
最后将链表前半部分和反转后的后半部分链表逐节点进行比较判断。

class PalindromeList {
  public:
    bool chkPalindrome(ListNode* A) {
        if (A == nullptr || A->next == nullptr)
            return true;

        ListNode* slow, *fast;
        slow = fast = A;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }

        ListNode* prev, *cur, *nxt;
        prev = nullptr;
        cur = slow;
        while (cur) {
            nxt = cur->next;
            cur->next = prev;
            prev = cur;
            cur = nxt;
        }

        while (A && prev) {
            if (A->val != prev->val)
                return false;
            
            A = A->next;
            prev = prev->next;
        }
        return true;
    }

};

左叶子之和

左叶子之和_牛客题霸_牛客网 (nowcoder.com)

class Solution {
  public:
    void _helper(TreeNode* root, int& sum) {
        if (root == nullptr)
            return;
        if (root->left && !root->left->left && !root->left->right)
            sum += root->left->val;
            
        _helper(root->left, sum);
        _helper(root->right, sum);
    }
    int sumOfLeftLeaves(TreeNode* root) {
        int sum = 0;
        _helper(root, sum);
        return sum;
    }
};

另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

class Solution {
public:
    bool isSubtree(TreeNode* s, TreeNode* t) {
        if (!s && !t)
            return true;

        // 代码走到这里 已经保证s t不全空
        if (!s || !t)
            return false;

        return isSameTree(s, t) || isSubtree(s->left, t) ||
               isSubtree(s->right, t);
    }

    bool isSameTree(TreeNode* s, TreeNode* t) {
        if (!s && !t)
            return true; 
        if (!s || !t)
            return false; 
        return (s->val == t->val) && isSameTree(s->left, t->left) &&
               isSameTree(s->right, t->right);
    }
};

归并排序

递归

#include <iostream>
#include <vector>

void merge(std::vector<int>& arr, int left, int mid, int right) {
    std::vector<int> leftArr(arr.begin() + left, arr.begin() + mid + 1);
    std::vector<int> rightArr(arr.begin() + mid + 1, arr.begin() + right + 1);

    int i = 0, j = 0, k = left;

    while (i < leftArr.size() && j < rightArr.size()) {
        if (leftArr[i] <= rightArr[j]) {
            arr[k++] = leftArr[i++];
        } else {
            arr[k++] = rightArr[j++];
        }
    }

    while (i < leftArr.size()) {
        arr[k++] = leftArr[i++];
    }

    while (j < rightArr.size()) {
        arr[k++] = rightArr[j++];
    }
}

void merge_sort_recursive(std::vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        merge_sort_recursive(arr, left, mid);
        merge_sort_recursive(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

int main() {
    int N;
    std::cin >> N;
    std::vector<int> data(N);

    for (int i = 0; i < N; ++i) {
        std::cin >> data[i];
    }

    merge_sort_recursive(data, 0, N - 1);

    for (const auto& num : data) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

非递归

#include <iostream>
#include <vector>

void merge(std::vector<int>& arr, int left, int mid, int right) {
    std::vector<int> leftArr(arr.begin() + left, arr.begin() + mid + 1);
    std::vector<int> rightArr(arr.begin() + mid + 1, arr.begin() + right + 1);

    int i = 0, j = 0, k = left;

    while (i < leftArr.size() && j < rightArr.size()) {
        if (leftArr[i] <= rightArr[j]) {
            arr[k++] = leftArr[i++];
        } else {
            arr[k++] = rightArr[j++];
        }
    }

    while (i < leftArr.size()) {
        arr[k++] = leftArr[i++];
    }

    while (j < rightArr.size()) {
        arr[k++] = rightArr[j++];
    }
}

void merge_sort_iterative(std::vector<int>& arr)
{
    int n = arr.size();
    for (int size = 1; size < n; size *= 2) 
    {
        for (int left = 0; left < n; left += 2 * size)
        {
            int mid = std::min(left + size - 1, n - 1);
            int right = std::min((left + 2 * size - 1), (n - 1));
            if (mid < right) 
            {
                merge(arr, left, mid, right);
            }
        }
    }
}

int main() {
    int N;
    std::cin >> N;
    std::vector<int> data(N);

    for (int i = 0; i < N; ++i) {
        std::cin >> data[i];
    }

    merge_sort_iterative(data);

    for (const auto& num : data) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

类与对象

已知表达式++a中的"++"是作为成员函数重载的运算符,则与++a等效的运算符函数调用形式为：a.operator++()；后置++a++ == a.operator++(0)
c++中，ClassA的构造函数和析构函数的执行次数分别为：程序可能崩溃
```
ClassA *pclassa=new ClassA[5];
delete pclassa;
```

resize和reserve

int main()
{
    string str("Hello Bit.");
    str.reserve(111);
    str.resize(5);
    str.reserve(50);
    cout << str.size() << ":" << str.capacity() << endl;
    return 0;
}
// linux：5：50
// vs：   5：111

迭代器失效1.0

int main()
{
    int ar[] = { 1,2,3,4,0,5,6,7,8,9 };
    int n = sizeof(ar) / sizeof(int);
    vector<int> v(ar, ar + n);
    vector<int>::iterator it = v.begin();
    while (it != v.end())
    {
        if(*it == 0)
            v.erase(it);
        else
            cout<<*it;
        it++;
    }
    return 0;
}

erase方法从vector容器中删除一个或多个元素，并调整vector的大小。删除元素后，后续元素会被移动以填补删除的空隙，此时it指向5，所有指向被删除元素之后的迭代器都会失效，即此时it失效linux允许执行 it++操作，故输出12346789；vs不允许，故崩溃。

解决

if(*it == 0)
    it = v.erase(it);
else
{
    cout<<*it;
    it++;
}

迭代器失效2.0

int main()
{
    Container cont = { 1, 2, 3, 4, 5};
    Container::iterator iter, tempIt;
    for (iter = cont.begin(); iter != cont.end();)
    {
        tempIt = iter;
        ++iter;
        cont.erase(tempIt);
    }
}
// 会导致代码片段崩溃的Container类型是（vector和deque）

vector和deque，erase操作会使所有指向被删除元素之后元素的迭代器、引用和指针都失效。

但对于list，erase操作只会使指向被删除元素的迭代器失效，其他迭代器、引用和指针仍然有效。

由题知虽然++iter迭代器了，但用erase(tempit)以后，vector、deque底层是连续空间，删除会挪动数据，最终导致iter意义改变，迭代器就已失效了。但是list，不是连续空间，删除以后tempIt虽然失效了，但是不影响iter。

引用

引用在定义时必须被初始化，并且必须绑定到一个已经存在的对象。
引用一旦被初始化并绑定到一个对象，就不能改变其绑定。
引用本身不是一个独立的对象，它只是被绑定对象的一个别名，因此不能定义引用的引用。
引用本身不是对象，因此不能有指向引用的指针。指针可以指向对象，但不能直接指向引用。

析构函数与this指针

class A
{
public:
   ~A()
    {
        delete this;
        this = NULL;
    }
};
析构函数内部调用delete -- 无限递归
this的类型`A* const this`，this不能更改指向，编译错误。故该程序在编译时就无法通过。

私有重写虚函数

class A
{
public:
    virtual void f()
    {
        cout << "A::f()" << endl;
    }
};
class B : public A
{
private:
    virtual void f()
    {
        cout << "B::f()" << endl;
    }
};
int main()
{
    A *pa = (A *)new B;
    pa->f();
    return 0;
}
// B::f()

编译时，不会确定具体调用哪个虚函数；只是进行语法检测，编译器检测到pa是A类型的指针，编译器会确定两件事：A类中有没有f()函数 + 该函数是否是public。如果满足这两个条件，那么编译通过，否则编译报错。显而易见，该代码可以编译通过，在运行时，pa是指向子类的基类指针，回去子类的虚表调用f()，改函数已被B重写故调用B::f()。

静态类型: 声明变量时给的类型A * pa=newB; pa的静态类型就是A * 。编译时看静态类型。

动态类型:实际指向或引用实体的类型pa的动态类型时B* ，运行时看的是动态类型。

判断题

被virtual修饰的函数称为虚函数【❌】被virtual修饰的成员函数称为虚函数。友元函数不属于成员函数，不能成为虚函数。

位图可以很方便的进行字符串的映射以及查找【❌】采用位图标记字符串时，必须先将字符串转化为整形的数字，找到位图中对应的
比特位，但是在字符串转整形的过程中，可能会出现不同字符串转化为同一个整形数字，即冲突，因此一般不会直接用位图处理字符串。

set中存<key, key> unordered_set中存< key >

unordered _ map和unordered _ set：它们在进行元素插入时，都得要通过key的比较去找待插入元素的位置。【❌】不需要比较，只需要通过哈希函数，就可以确认元素需要存储的位置。

AVL树是一定需要旋转，红黑树不一定，比如插入的节点的parent节点为红色，uncle节点也为红色，那么只需要将父节点和叔叔节点颜色变黑，将grandfather的颜色变红，该种情况下，红黑树是不需要进行旋转的。AVL树和红黑树中序遍历都可以得到有序序列，因为它们都是二叉搜索树。【✔】

插入时，AVL树最多只需要旋转两次：新结点插入前树已经是AVL树了，新结点插入后，如果导致某结点平衡因子为2或-2时，AVL树平衡性遭到破坏，以该结点为根的二叉树局部高度增加了一层，旋转完成后，该棵树高度和插入新结点前高度一致，所以旋转后对整棵树没有任何影响，旋转结束后树满足AVL树的特性。该旋转可能是单旋也可能是双旋，因此插入时AVL树最多只需要旋转两次。

删除时，只要某个节点的平衡因子不满足特性时，只需要对该棵子树进行旋转，就可以使AVL树再次平衡。错误，可能需要旋转多次，子树旋转后，其高度降低了一层，其上层可能也需要跟着旋转。

AVL树的节点中必须维护平衡因子，因为要依靠其平衡因子是否需要旋转以维护其平衡性，平衡因子不是必须要维护的，在操作时也可以直接通过高度函数来算，只不过比。较麻烦

AVL树的双旋转只需要直接使用对应的单旋转即可：不能直接使用单旋转，因为两个单旋转完成后，还需要对部分节点的平衡因子进
行更新

二叉树的后序非递归遍历中，需要的额外空间：需要一个栈模拟递归的过程，一个顺序表保存节点。同时还需要一个prev节点保存刚刚遍历过的结点来解决某个结点有右子树时的死循环问题。

多态经典代码

class A
{
public:
    A()
        : m_iVal(0)
    {
        test();
    }

    virtual void func()
    {
        std::cout << m_iVal << ' ';
    }

    void test()
    {
        func();
    }

public:
    int m_iVal;
};
class B : public A
{
public:
    B()
    {
        test();
    }
    
    virtual void func()
    {
        ++m_iVal;
        std::cout << m_iVal << ' ';
    }
};
int main(int argc, char *argv[])
{
    A *p = new B;
    p->test();
    return 0;
}
// 0 1 2

编程训练

杨辉三角

class Solution 
{
  public:
    vector<vector<int>> generate(int numRows) 
    {
        vector<vector<int>> t;
        for (int i = 0; i < numRows; i++)
        {
            vector<int> row(i + 1, 1);
            for (int j = 1; j < i; j++) 
            {
               row[j]  = t[i - 1][j - 1] + t[i - 1][j];
            }
            t.push_back(row);
        }

        return t;
    }
};

字符串乘积

在这里插入图片描述

模拟手工计算两个大数相乘，从低位到高位，每次计算一对对应位的乘积，然后加上进位和之前的结果，更新当前位的结果和进位。

class Solution
{
public:
    string solve(string num1, string num2)
    {
        if (num1 == "0" || num2 == "0")
        {
            return "0";
        }
        reverse(num1.begin(), num1.end());
        reverse(num2.begin(), num2.end());

        string ans(num1.size() + num2.size(), '0');
        int carry = 0;

        for (int i = 0; i < num1.size(); ++i)
        {
            for (int j = 0; j < num2.size(); ++j)
            {
                // 当前位的结果等于之前的进位加上两数当前位的乘积和之前计算的结果
                carry += (num1[i] - '0') * (num2[j] - '0') + (ans[i + j] - '0');
                // 计算当前位的结果，保存到结果中
                ans[i + j] = carry % 10 + '0';
                // 更新进位
                carry /= 10;
            }
            // 如果最后还有进位，将进位加到结果中
            if (carry > 0)
            {
                ans[i + num2.size()] = (carry + '0');
                carry = 0;
            }
        }
        // 如果最高位为0（即未被使用），则去掉最高位
        if (ans.size() >= 2 && ans.back() == '0')
        {
            ans.pop_back();
        }
        // 将结果反转回正确的顺序
        reverse(ans.begin(), ans.end());
        // 返回结果
        return ans;
    }
};

逻辑更清晰用vector暂存每位结果只加不进

class Solution
{
public:
    string solve(string s, string t)
    {
        // 其中一个数为0
        if (s == "0" || t == "0")
        {
            return "0";
        }
        int sNum = s.size();
        int tNum = t.size();
        vector<int> tmp(sNum + tNum); // save per add
        string ret;
        // reverse s t
        reverse(s.begin(), s.end());
        reverse(t.begin(), t.end());
        // only add not carry
        for (int i = 0; i < sNum; i++)
        {
            for (int j = 0; j < tNum; j++)
            {
                tmp[i + j] += (s[i] - '0') * (t[j] - '0');
            }
        }
        // deal carry
        int carry = 0;
        for (auto per : tmp)
        {
            per += carry;
            ret += per % 10 + '0';
            carry = per / 10;
        }
        // max high carry
        while (carry)
        {
            ret += carry % 10 + '0';
            carry /= 10;
        }
        // prev zero
        while (ret.size() >= 2 && ret.back() == '0')
        {
            ret.pop_back();
        }
        reverse(ret.begin(), ret.end());
        return ret;
    }
};

二叉树前序遍历成字符串

606. 根据二叉树创建字符串 - 力扣（LeetCode）

一棵树只有这五种情况：

空

只有根节点

只有左子树

只有右子树

左右子树都有

法一

如果左子树为真，需要加括号
如果左子树为空，右子树为真，需要给左子树加()不破坏输入与输出一一映射的关系
如果左右子树都为空，则不需要加括号
当右子树为空，不需要加括号

class Solution {
    public:
    string tree2str(TreeNode* root) {
        if (root == nullptr)
        {
            return "";
        }
        string ret;
        ret += to_string(root->val);

        //左子树为真，需要加括号。如果没有左子树，但是有右子树为了不破坏输入与输出一一映射的关系，同样需要加括号
        if (root->left || root->right)
        {
            ret+= '(';
            ret += tree2str(root->left);
            ret += ')';
        }
        if (root->right)
        {
            ret+= '(';
            ret += tree2str(root->right);
            ret += ')';
        }
        return ret;
    }
};

法二：

当节点为叶子节点时不需要加括号。
当左子树存在，右子树为空时，需要给左子树加上括号。

当左右子树都为真就去递归加括号或者左子树为空右子树为真，这个时候为了不破坏输入与输出一一映射的关系，需要加左括号

class Solution {
    public:
    string tree2str(TreeNode *root) {
        // 空树
        if (root == nullptr) {
            return "";
        }
        // 只有根节点
        if (root->left == nullptr && root->right == nullptr) {
            return to_string(root->val);
        }
        // 只有左子树
        if (root->right == nullptr) {
            return to_string(root->val) + "(" + tree2str(root->left) + ")";
        }
        // 只有右子树 + 左右子树都有
        return to_string(root->val) + "(" + tree2str(root->left) + ")(" +
            tree2str(root->right) + ")";
    }
};

法三：迭代

class Solution {
public:
    string tree2str(TreeNode *root) {
        string ans = "";
        stack<TreeNode *> st;
        st.push(root);
        unordered_set<TreeNode *> vis;
        while (!st.empty()) {
            auto node = st.top();
            if (vis.count(node)) {
                if (node != root) {
                    ans += ")";
                }
                st.pop();
            } else {
                vis.insert(node);
                if (node != root) {
                    ans += "(";
                }
                ans += to_string(node->val);
                if (node->left == nullptr && node->right != nullptr) {
                    ans += "()";
                }
                if (node->right != nullptr) {
                    st.push(node->right);
                }
                if (node->left != nullptr) {
                    st.push(node->left);
                }
            }
        }
        return ans;
    }
};

数组的交集

只求交集不管是否重复

class Solution 
{
public:
	vector<int> intersection(vector<int>& nums1, vector<int>& nums2) 
	{
		unordered_set<int> us1, us2;

		for (auto& e : nums1)
			us1.insert(e);

		for (auto& e : nums2)
			us2.insert(e);
        
		return get(us1, us2);
	}

	vector<int> get(unordered_set<int>& us1, unordered_set<int>& us2) 
	{
		if (us1.size() > us2.size())
		return get(us2, us1);

		vector<int> v;
		for (auto& e : us1)
		{
			if (us2.count(e))
				v.push_back(e);
		}
		return v;
	}
};

交集元素有多个

//法一：排序+双指针
//1.1 用multiset排序
class Solution
{
    public:
    vector<int> intersect(vector<int> &nums1, vector<int> &nums2)
    {
        multiset<int> ms1(nums1.begin(), nums1.end());
        multiset<int> ms2(nums2.begin(), nums2.end());
        multiset<int>::iterator it1 = ms1.begin();
        multiset<int>::iterator it2 = ms2.begin();
        vector<int> v;
        while (it1 != ms1.end() && it2 != ms2.end())
        {
            if (*it1 < *it2)
                ++it1;
            else if (*it1 > *it2)
                ++it2;
            else
            {
                v.push_back(*it1);
                ++it1;
                ++it2;
            }
        }
        return v;
    }
};
//1.2 用sort排序
class Solution 
{
    public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2)
    {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size(), length2 = nums2.size();
        vector<int> intersection;
        int index1 = 0, index2 = 0;
        while (index1 < length1 && index2 < length2)
        {
            if (nums1[index1] < nums2[index2]) 
            {
                index1++;
            } 
            else if (nums1[index1] > nums2[index2]) 
            {
                index2++;
            } 
            else 
            {
                intersection.push_back(nums1[index1]);
                index1++;
                index2++;
            }
        }
        return intersection;
    }
};
//法二：哈希表
class Solution 
{
    public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) 
    {
        if (nums1.size() > nums2.size()) 
        {
            return intersect(nums2, nums1);
        }
        unordered_map <int, int> m;
        for (int num : nums1)
        {
            ++m[num];
        }
        vector<int> intersection;
        for (int num : nums2) 
        {
            if (m.count(num)) 
            {
                intersection.push_back(num);
                --m[num];
                if (m[num] == 0)
                {
                    m.erase(num);
                }
            }
        }
        return intersection;
    }
};

二叉树的非递归前序遍历

class Solution {
public:
   vector<int> preorderTraversal(TreeNode* root)
{
	vector<int> v;
	stack<TreeNode*> st;
	TreeNode* cp = root;
	while (cp || !st.empty())
	{
		//左路结点
		while (cp)
		{
			v.push_back(cp->val);
			st.push(cp);
			cp = cp->left;
		}
		//左路结点的右子树
		TreeNode* top = st.top();
		st.pop();
		cp = top->right;
	}
	return v;
}
};

连续子数组的最大乘积

#include<vector>
#include<cstdlib>
#include<climits>
#include<iostream>
using namespace std;
//暴力解法
int maxProductSubarray(vector<int>& nums) 
{
    int n = nums.size();
    int maxnum = INT_MIN;
    for (int start = 0; start < n; ++start) 
    {
        //更新cur 下次重新记录start位置的最大乘积
        int cur = 1;
        for (int end = start; end < n; ++end) 
        {
            //计算从start位置开始向后的乘积
            cur *= nums[end];
            if (cur > maxnum)
            {
                maxnum = cur;
            }
        }
    }
    return maxnum;
}
int main() 
{
    int n;
    cin >> n;
    vector<int> nums(n);
    for (int i = 0; i < n; ++i) 
    {
        cin >> nums[i];
    }
    int result = maxProductSubarray(nums);
    cout << result << endl;
    return 0;
}

class Solution {
  public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n + 1), g(n + 1);
        f[0] = g[0] = 1;
        int ret = INT_MIN;
        for (int i = 1; i <= n; i++) {
            int x = nums[i - 1];
            int y = f[i - 1] * x;
            int z = g[i - 1] * x;
            f[i] = max(x, max(y, z));
            g[i] = min(x, min(y, z));
            ret = max(ret, f[i]);
        }
        return ret;
    }
};