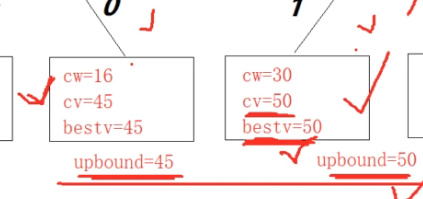
分支限界算法解决0-1背包问题-FIFO队列
广度优先遍历:一层一层遍历,每层是从左向右遍历。
int w[] = { 16,15,15 };//物品的重量
int v[] = { 45,25,25 };//物品的价值
背包的容量c是30,图解如下:
最优节点是图中叶子节点打√的那个节点
相当于左子树加约束条件了,右子树进行限界了。
我们把根节点描述成nullptr
//分支限界算法 - 01背包问题 FIFO队列
int w[] = { 16,15,15 };//物品的重量
int v[] = { 45, 25, 25 };//物品的价值
int c = 30;//背包的容量
const int n = sizeof(w) / sizeof(w[0]);//物品的个数
int cw = 0;//已选择物品的重量
int cv = 0;//已选择物品的价值
int bestv = 0;//装入背包的物品的最优价值
//描述节点类型
struct Node
{
Node(int w, int v, int l, Node *p, bool left)
{
weight = w;
value = v;
level = l;
parent = p;
isleft = left;
}
int weight;//已选择物品的总重量
int value;//已选择物品的总价值
int level;//节点所在的层数
Node *parent;//记录父节点
bool isleft;//节点是否被选择
};
Node *bestnode = nullptr;//记录最优解的叶子节点
queue<Node*> que;//广度遍历需要的FIFO队列
void addLiveNode(int w, int v, int l, Node *parent, bool isleft)
{
Node *node = new Node(w, v, l, parent, isleft);
que.push(node);
if (l == n && v == bestv)
{
bestnode = node;
}
}
//求价值上界
int maxBound(int i)
{
int bound = 0;
for (int level = i + 1; level < n; ++level)
{
bound += v[level];
}
return bound;
}
int main()
{
int i = 0;//起始的层数
Node *node = nullptr;//记录父节点
while (i < n)
{
//选择物品i
int wt = cw + w[i];
if (wt <= c)
{
if (cv + v[i] > bestv)
{
bestv = cv + v[i];
}
//把左孩子加入活结点队列当中
addLiveNode(cw+w[i], cv+v[i], i+1, node, true);
}
//不选择物品i
int upbound = maxBound(i);
if (cv + upbound >= bestv)
{
addLiveNode(cw, cv, i + 1, node, false);
}
node = que.front();
que.pop();
i = node->level;
cw = node->weight;
cv = node->value;
}
cout << bestv << endl;
int x[n] = { 0 };
for (int j = n - 1; j >= 0; --j)
{
x[j] = bestnode->isleft ? 1 : 0;
bestnode = bestnode->parent;
}
for (int v : x)
{
cout << v << " ";
}
cout << endl;
return 0;
}
剪掉不必要的:
分支限界算法解决0-1背包问题-优先级队列
以最小耗费,最接近最优值的方式遍历子集树,解空间
优先级队列可以更加快速的到达叶子结点
我们选择下一个扩展节点不再总是从队头取出,而是看优先级。
所以我们把价值上界成为节点的一个成员变量
通过upbound进行优先级比较
upbound大的先出队处理
选择优先级队列里面有这2个节点,95>50,根节点的左孩子节点优先级高,它出队,处理它,然后它不会向左走了,因为16+15=31>30,已经超过背包容量了,不满足条件,所以它往右边看,它的右孩子的upbound是45+25=70
,把它的右孩子入队
按照优先级,70>50,所以还是刚才处理的根节点的左孩子的右孩子节点出队,然后处理它,它不会往左走,因为已经16+15=31,已经超过背包的容量了,然后它走右边,右孩子的upbound值为45,然后入队
现在优先级队列中的节点是:刚才处理的这个upbound值为45的叶子节点和根节点的右孩子节点(upbound是50)
如果此时刚才处理的这个叶子节点的upbound是最大的,那么它出队,我们一看,这个节点是叶子节点了,那这个就是最优解的了。但是很可惜,这个叶子节点的upbound值小于根节点的右孩子的upbound值。
所以,根节点的右孩子出队。
它走向它的左孩子,它的左孩子的upbound值是50,然后入队,此时优先级队列中的节点是:当前节点和upbound为45的叶子节点了。当前节点的优先级高,所以当前节点出队
当前节点走向它的左孩子,它的左孩子的upbound值是50,入队,此时优先级队列中是
然后右边这个节点的优先级大,先出队,发现是叶子节点,最优解就找到了!!!
优先级队列可以更加快速的到达叶子结点!!!
#include <iostream>
#include <queue>
#include <functional>
#include <vector>
using namespace std;
//分支限界算法 - 01背包问题 优先级队列
int w[] = { 16,15,15 };//物品的重量
int v[] = { 45, 25, 25 };//物品的价值
int c = 31;//背包的容量
const int n = sizeof(w) / sizeof(w[0]);//物品的个数
int cw = 0;//已选择物品的重量
int cv = 0;//已选择物品的价值
int bestv = 0;//装入背包的物品的最优价值
//描述节点类型
struct Node
{
Node(int w, int v, int l, int up, Node *p, bool left)
{
weight = w;
value = v;
level = l;
parent = p;
isleft = left;
upbound = up;
}
int weight;//已选择物品的总重量
int value;//已选择物品的总价值
int level;//节点所在的层数
Node *parent;//记录父节点
bool isleft;//节点是否被选择
int upbound;//节点的价值上界, 从这个节点往下,最多能选择的物品产生的总价值
};
//queue<Node*> que; //广度遍历需要的FIFO队列
priority_queue<Node*, vector<Node*>, function<bool(Node*, Node*)>> que([](Node*n1, Node*n2)->bool //默认是大根堆
{
return n1->upbound < n2->upbound;
});
void addLiveNode(int w, int v, int l, int up, Node *parent, bool isleft)
{
Node *node = new Node(w, v, l, up, parent, isleft);
que.push(node);
//用优先级队列就不用标记产生最优解的叶子节点了,因为优先级队列到达某一个叶子节点时,最优值就产生了
/*if (l == n && v == bestv)
{
bestnode = node;
}*/
}
//求价值上界
int maxBound(int i)
{
int bound = cv;
for (int level = i; level < n; ++level)
{
bound += v[level];
}
return bound;
}
int main()
{
int i = 0;//起始的层数
Node *node = nullptr;//记录父节点
int upbound = maxBound(0);
while (i < n)
{
//选择物品i
int wt = cw + w[i];
if (wt <= c) {
if (cv + v[i] > bestv)
{
bestv = cv + v[i];
}
//把左孩子加入活结点队列当中
addLiveNode(cw + w[i], cv + v[i], i + 1, upbound, node, true);
}
//不选择物品i
upbound = maxBound(i+1);//i+1表示第一个未被处理的物品的数组下标
if (upbound >= bestv)
{
addLiveNode(cw, cv, i + 1, upbound, node, false);
}
node = que.top();
que.pop();
i = node->level;
cw = node->weight;
cv = node->value;
upbound = node->upbound;
}
cout << bestv << endl;
int x[n] = { 0 };
for (int j = n - 1; j >= 0; --j)
{
x[j] = node->isleft ? 1 : 0;
node = node->parent;
}
for (int v : x)
{
cout << v << " ";
}
cout << endl;
return 0;
}