每日一题：Leetcode-124 二叉树中的最大路径和

力扣题目

解题思路

java代码

力扣题目：

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

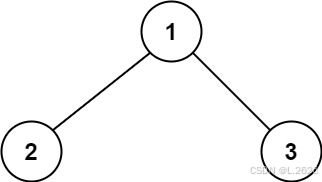
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

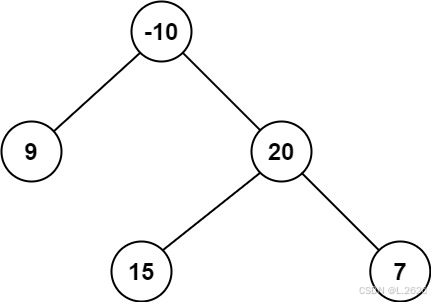
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

解题思路：

代码的主要部分是一个名为 maxPathSum 的函数，它接受一个 TreeNode 类型的参数 root，代表树的根节点。该函数使用了递归的方式来计算每个节点的最大贡献值，并更新全局变量 maxSum 来记录已知的最大路径和。

maxGain 函数是 maxPathSum 的辅助函数，用于递归地计算每个节点的最大贡献值。如果一个节点的左子节点或右子节点的贡献值大于0，则将该子节点加入路径；否则，不加入。

在 main 函数中，创建了两棵二叉树，并调用了 maxPathSum 函数来计算它们的最大路径和，并打印结果。

java代码：

package org.example.mouth7.today715;


public class Leetcode124 {
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(-4);
        root.left.right = new TreeNode(5);
        root.right.left = new TreeNode(6);
        TreeNode root1 = new TreeNode(2);
        root1.left = new TreeNode(1);
        root1.right = new TreeNode(3);
        root1.left.left = new TreeNode(4);
        root1.right.left = new TreeNode(5);
        System.out.println(maxPathSum(root1));
    }

    static int maxSum = Integer.MIN_VALUE;

    public static int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }

    public static int maxGain(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node.val + leftGain + rightGain;

        // 更新答案
        maxSum = Math.max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node.val + Math.max(leftGain, rightGain);
    }


}
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
    }
}

更多详细内容同步到公众号，感谢大家的支持！

每天都会给刷算法的小伙伴推送明日一题，并且没有任何收费项

每日一题：Leetcode-124 二叉树中的最大路径和

力扣题目：

解题思路：

java代码：

悦读