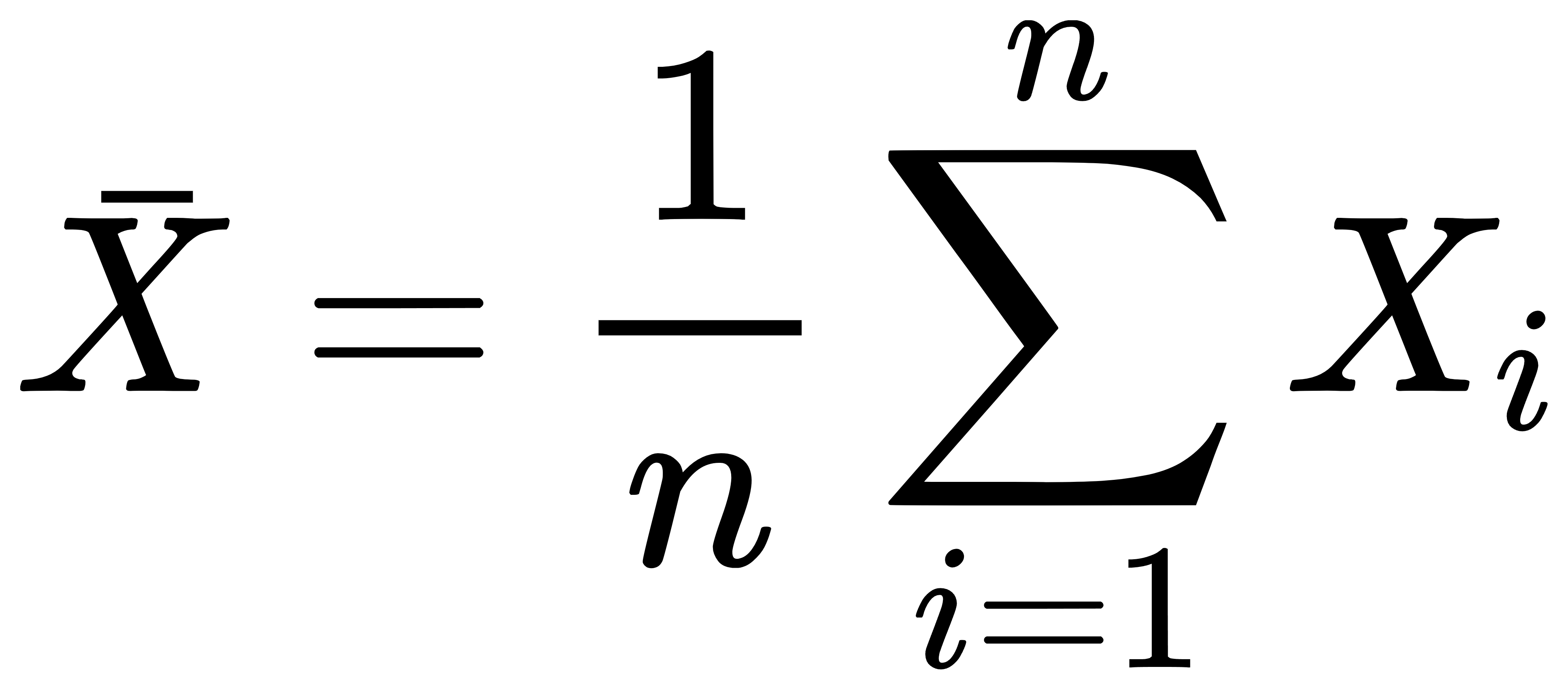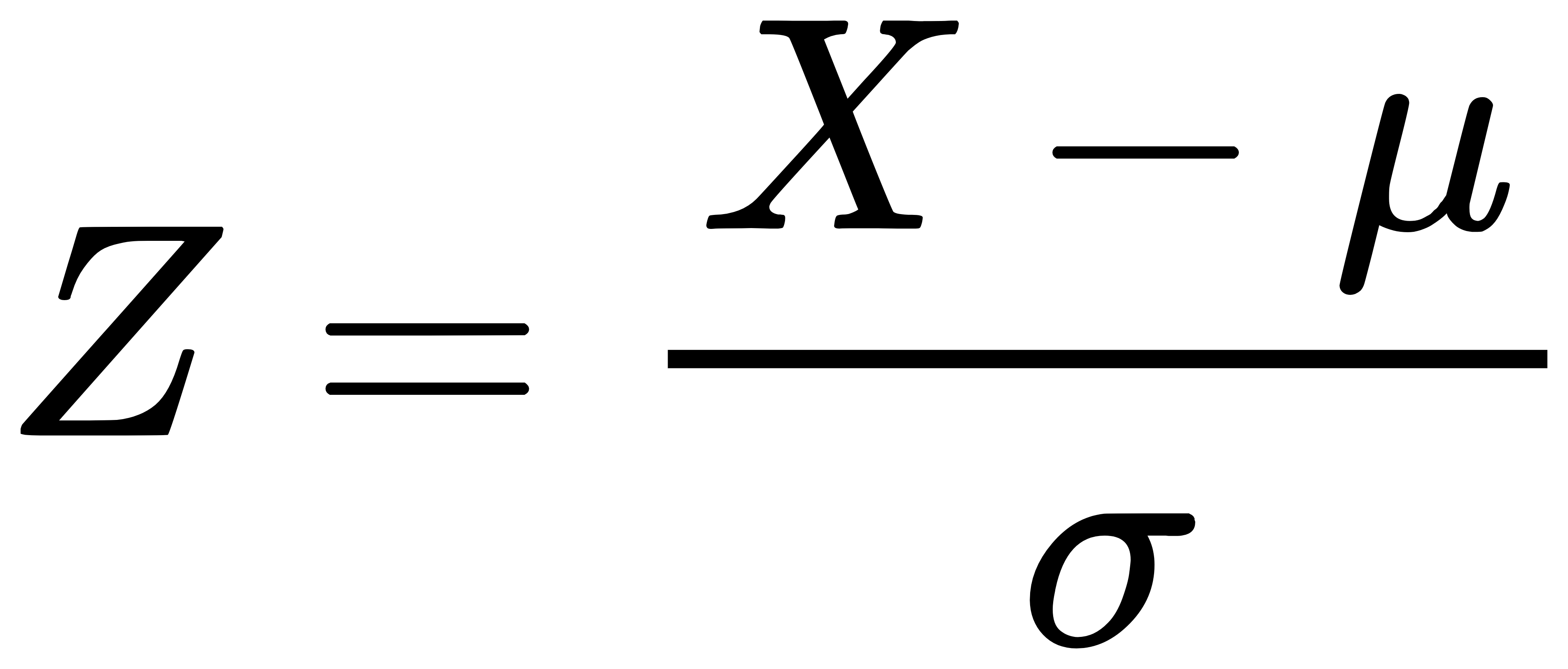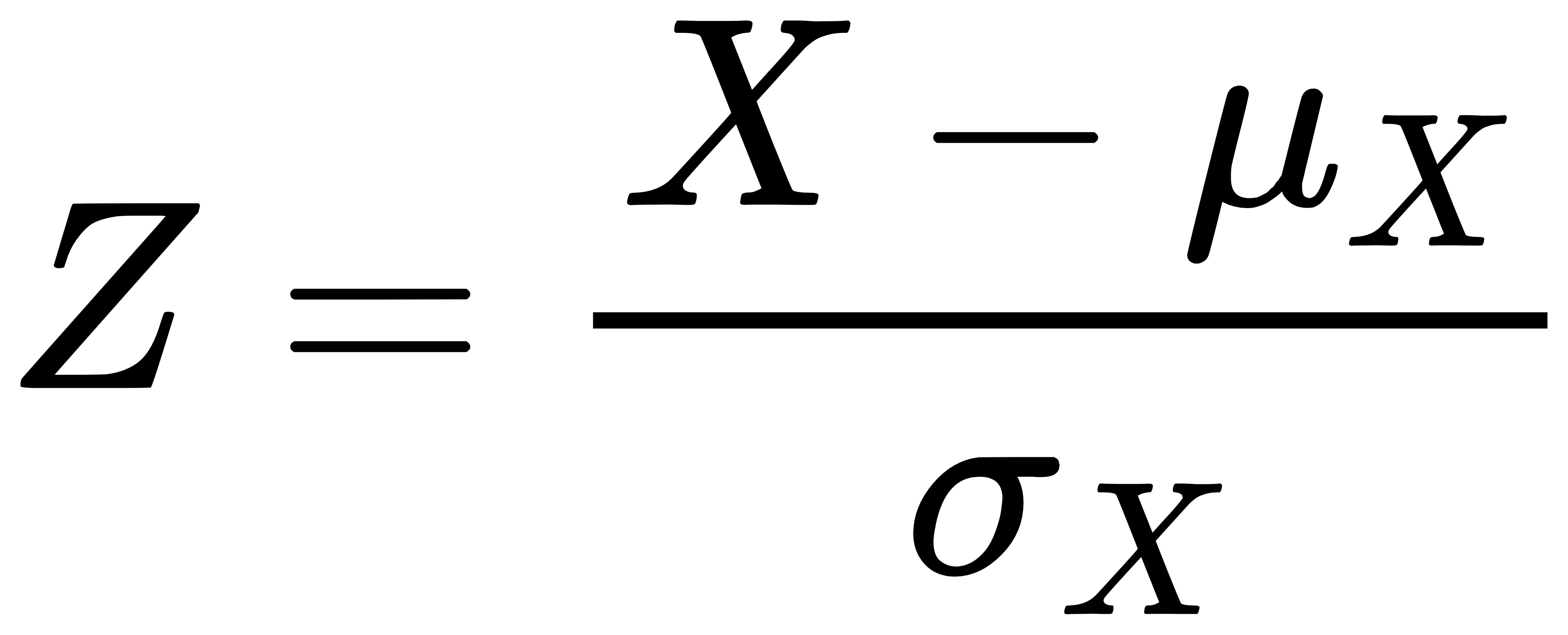数据清理和数据标准化

数据清洗（Data Cleaning）

数据清洗是指处理缺失值和异常值，以提高数据质量和模型性能。它是数据预处理过程中至关重要的一步，有助于确保模型训练的准确性和可靠性。

原理

缺失值处理

处理缺失值的方法包括删除含有缺失值的样本或特征，或者使用插值、均值、中位数、众数等方法填补缺失值。

异常值处理

处理异常值的方法包括使用统计方法（如Z-Score）或基于模型的方法（如IQR）。

核心公式

处理缺失值

均值填补

对于一个有缺失值的特征列 X，其均值 Xˉ 计算为：

用这个均值填补缺失值。

处理异常值

Z-Score

标准化后的值 Z 计算公式为：

其中，μ 是均值，σ 是标准差。通常，∣Z∣>3 被认为是异常值。

案例

假设我们有一个关于房屋市场的数据集，其中包含房屋价格、房屋面积和用户评分等信息。数据集中可能存在缺失值和异常值，我们需要对其进行清洗，以便后续的分析和建模。

数据集描述

House_ID: 房屋的唯一标识符
Price: 房屋价格（单位：千元）
Size: 房屋面积（单位：平方米）
Rating: 用户评分（1到5分）

代码实现

import pandas as pd
import numpy as np

# 创建虚构数据集
np.random.seed(42)
data = {
    'House_ID': range(1, 101),
    'Price': np.random.normal(loc=300, scale=50, size=100),  # 房屋价格，均值300千元，标准差50千元
    'Size': np.random.normal(loc=150, scale=20, size=100),   # 房屋面积，均值150平方米，标准差20平方米
    'Rating': np.random.normal(loc=4, scale=0.5, size=100)   # 用户评分，均值4分，标准差0.5分
}

# 插入一些缺失值
data['Price'][np.random.choice(100, 10, replace=False)] = np.nan
data['Size'][np.random.choice(100, 8, replace=False)] = np.nan
data['Rating'][np.random.choice(100, 6, replace=False)] = np.nan

df = pd.DataFrame(data)

# 显示原始数据集
print("原始数据集：")
print(df.head(10))

# 使用均值填充缺失值
df['Price'].fillna(df['Price'].mean(), inplace=True)
df['Size'].fillna(df['Size'].mean(), inplace=True)
df['Rating'].fillna(df['Rating'].mean(), inplace=True)

# 显示填充缺失值后的数据集
print("\n填充缺失值后的数据集：")
print(df.head(10))

# 处理异常值

## 使用IQR（四分位距）方法来处理异常值
def remove_outliers(df, column):
    Q1 = df[column].quantile(0.25)
    Q3 = df[column].quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    return df[(df[column] >= lower_bound) & (df[column] <= upper_bound)]

df = remove_outliers(df, 'Price')
df = remove_outliers(df, 'Size')
df = remove_outliers(df, 'Rating')

# 显示处理异常值后的数据集
print("\n处理异常值后的数据集：")
print(df.head(10))

# 数据分析和可视化
import seaborn as sns
import matplotlib.pyplot as plt

# 绘制价格分布图
plt.figure(figsize=(12, 6))
sns.histplot(df['Price'], kde=True, bins=20)
plt.title('Price Distribution')
plt.xlabel('Price (in thousands)')
plt.ylabel('Frequency')
plt.show()

# 绘制房屋面积分布图
plt.figure(figsize=(12, 6))
sns.histplot(df['Size'], kde=True, bins=20)
plt.title('Size Distribution')
plt.xlabel('Size (in square meters)')
plt.ylabel('Frequency')
plt.show()

# 绘制评分分布图
plt.figure(figsize=(12, 6))
sns.histplot(df['Rating'], kde=True, bins=20)
plt.title('Rating Distribution')
plt.xlabel('Rating')
plt.ylabel('Frequency')
plt.show()

# 绘制房屋面积与价格的关系图
plt.figure(figsize=(12, 6))
sns.scatterplot(x='Size', y='Price', data=df)
plt.title('Size vs Price')
plt.xlabel('Size (in square meters)')
plt.ylabel('Price (in thousands)')
plt.show()

# 绘制房屋面积和评分的箱线图
plt.figure(figsize=(12, 6))
sns.boxplot(data=df[['Size', 'Rating']])
plt.title('Boxplot of Size and Rating')
plt.show()

解释

创建数据集：首先，我们创建一个包含房屋价格、房屋面积和用户评分的虚构数据集，并插入一些缺失值。
处理缺失值：使用均值填充数据集中的缺失值。
处理异常值：使用IQR方法检测和去除数据集中的异常值。
数据分析和可视化：使用Seaborn和Matplotlib库绘制数据的分布图和关系图，帮助我们更好地理解数据。

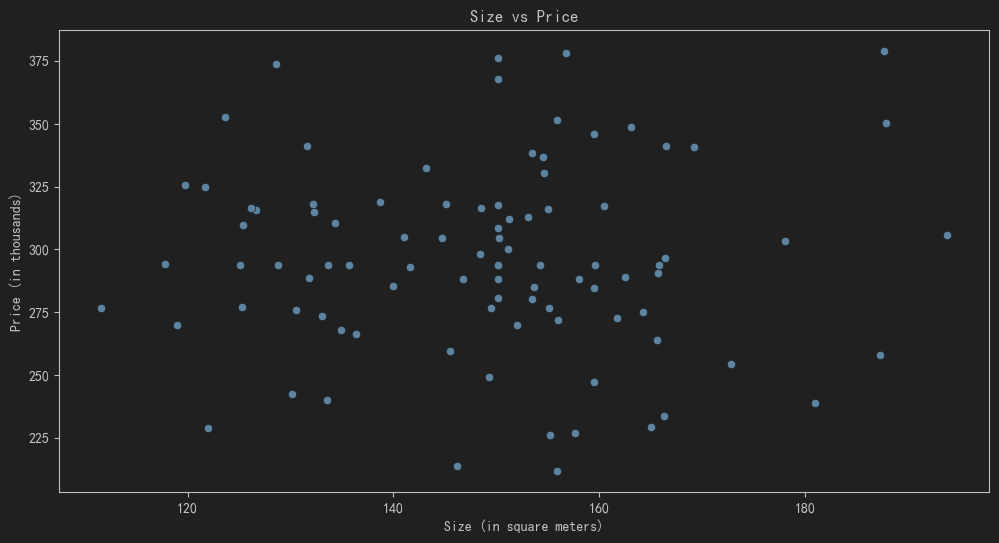
房屋面积与价格的关系图：

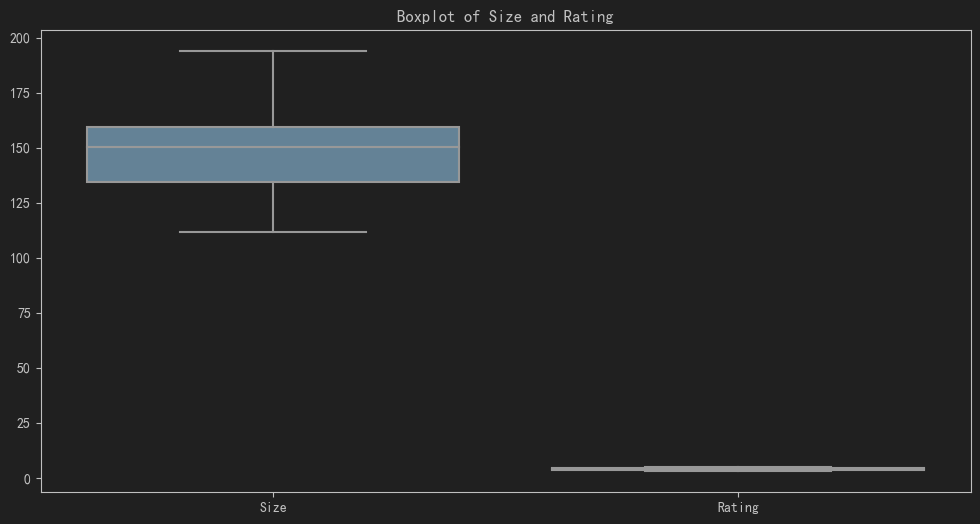
房屋面积和评分的箱线图：

通过以上步骤，我们可以有效地清洗数据，并对其进行初步分析和可视化，为后续的深入分析和建模奠定基础。

数据标准化（Standardization）

标准化是将数据转换为均值为0、标准差为1的分布，通常用于高斯分布的数据。这一过程可以减少特征之间量纲不一致的影响，从而提高某些机器学习算法的性能。

原理

标准化后的数据具有相同的尺度，减少特征之间量纲不一致的影响，有助于提高机器学习算法的性能。特别是在使用基于距离的算法（如KNN）和梯度下降优化的算法时，标准化是非常重要的。

核心公式

标准化公式：

其中，μ 是特征的均值，σ 是特征的标准差。

假设特征 X 的均值和标准差分别为 μX 和 σX，则标准化后的数据 Z为：

案例

假设我们有一个包含房屋面积和房屋价格的数据集，我们需要对这些数据进行标准化，以便后续的分析和建模。

代码实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# 1. 创建一个随机数据集（模拟房屋面积和房屋价格）
np.random.seed(42)
data = {
    'House_Size': np.random.normal(loc=150, scale=50, size=100),  # 房屋面积，均值150平方米，标准差50平方米
    'House_Price': np.random.normal(loc=300, scale=100, size=100)  # 房屋价格，均值300千元，标准差100千元
}

# 创建一个DataFrame
df = pd.DataFrame(data)

# 2. 对数据进行标准化
scaler = StandardScaler()
data_standardized = scaler.fit_transform(df)

# 创建标准化后的DataFrame
df_standardized = pd.DataFrame(data_standardized, columns=['House_Size', 'House_Price'])

# 3. 绘制标准化前后的数据分布直方图
plt.figure(figsize=(14, 6))

# 标准化前
plt.subplot(1, 2, 1)
plt.hist(df['House_Size'], bins=20, alpha=0.7, label='House_Size', color='blue')
plt.hist(df['House_Price'], bins=20, alpha=0.7, label='House_Price', color='green')
plt.title('Before Standardization')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()

# 标准化后
plt.subplot(1, 2, 2)
plt.hist(df_standardized['House_Size'], bins=20, alpha=0.7, label='House_Size', color='blue')
plt.hist(df_standardized['House_Price'], bins=20, alpha=0.7, label='House_Price', color='green')
plt.title('After Standardization')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()

plt.tight_layout()
plt.show()

# 4. 绘制标准化前后的数据散点图
plt.figure(figsize=(14, 6))

# 标准化前
plt.subplot(1, 2, 1)
plt.scatter(df['House_Size'], df['House_Price'], color='blue', alpha=0.7)
plt.title('Before Standardization')
plt.xlabel('House_Size')
plt.ylabel('House_Price')

# 标准化后
plt.subplot(1, 2, 2)
plt.scatter(df_standardized['House_Size'], df_standardized['House_Price'], color='red', alpha=0.7)
plt.title('After Standardization')
plt.xlabel('House_Size')
plt.ylabel('House_Price')

plt.tight_layout()
plt.show()

解释

创建数据集：首先，我们创建一个包含房屋面积和房屋价格的虚构数据集，并存储在一个DataFrame中。
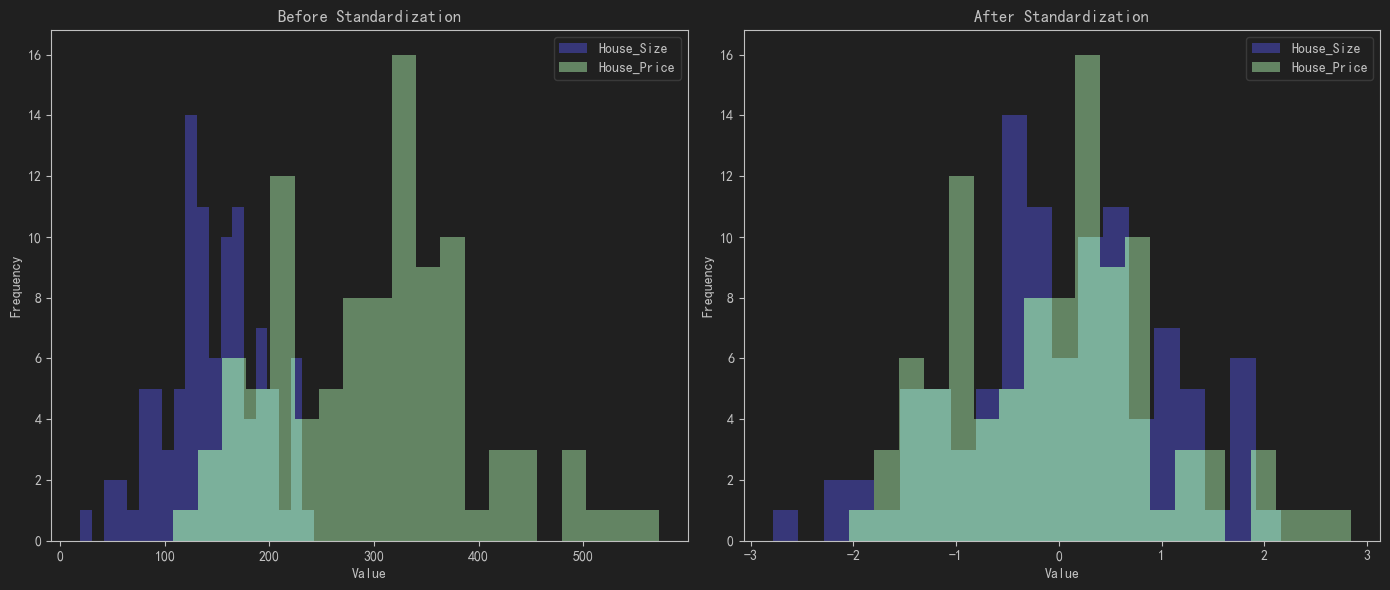
对数据进行标准化：使用StandardScaler对数据进行标准化，使其均值为0，标准差为1。
绘制标准化前后的数据分布直方图：通过直方图展示标准化前后的数据分布情况。

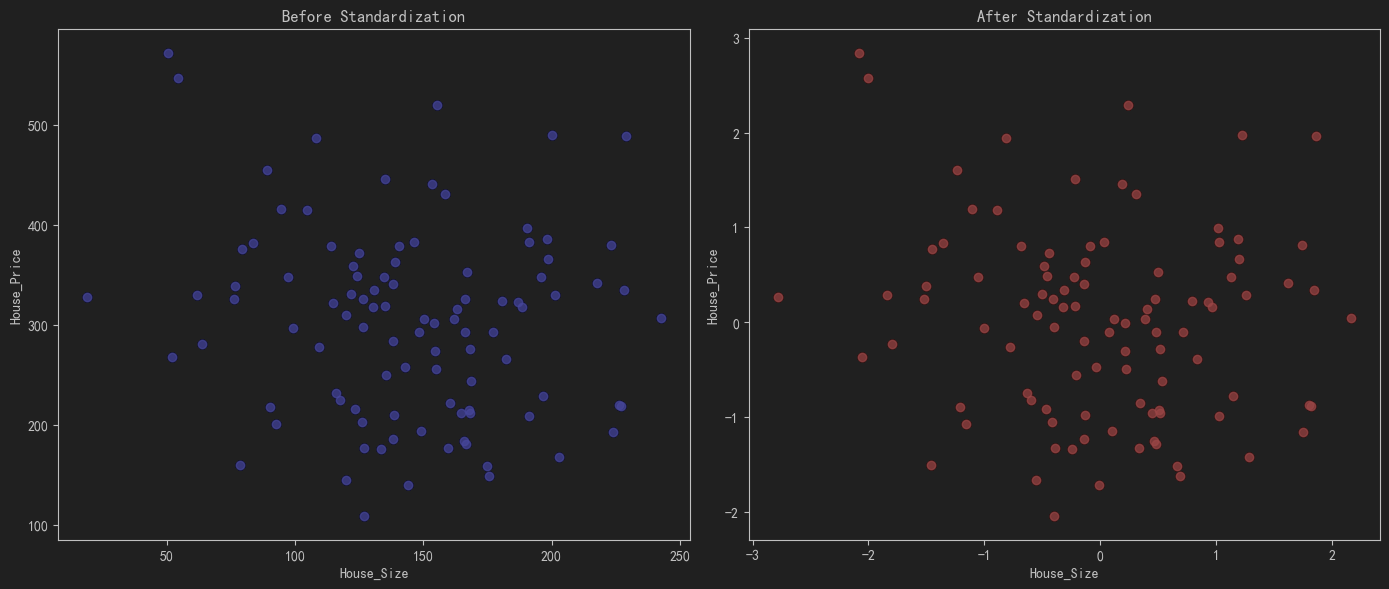
绘制标准化前后的数据散点图：通过散点图展示标准化前后的数据分布情况。

通过以上步骤，我们可以有效地标准化数据，并通过可视化手段展示标准化前后的数据变化。这对于理解标准化对数据的影响非常有帮助。