一、线性表(list)

线性表是最基本、最简单、也是最常用的一种数据结构。线性表*（linear list）*是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。

线性表的存储结构

• 顺序表
• 链表
  • 单链表
    • 动态单链表
    • 静态单链表
  • 双链表
  • 循环链表
    • 单循环链表
    • 双循环链表

以下我只实现了顺序表、单链表和双链表。

二、顺序表

顺序表是通过数组进行储存的结构

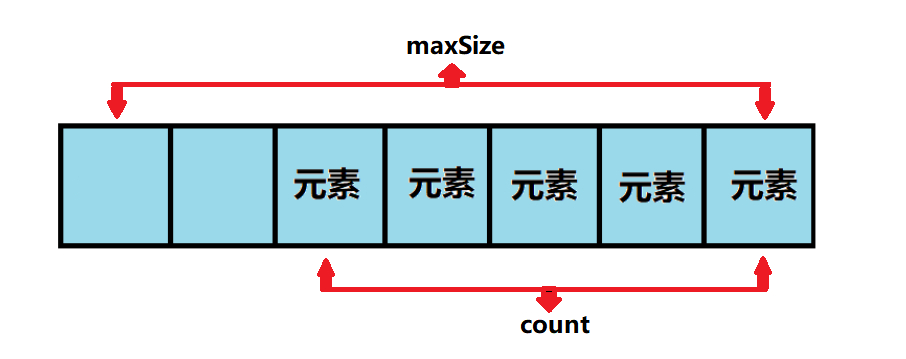
1. 结构模型图

2.顺序表的常用接口

功能描述：顺序栈容器常用的对外接口

构造函数：

• SeqList(); //构造函数
• SeqList(SeqList &s); //拷贝构造

大小操作：

• isEmpty();` //判断顺序表是否为空
• isFull();` //判断顺序表是否已满
• size(); ` //返回栈的大小
• resize(); // 扩容

插入删除：

• remove(int i)·; //在线性表中，位序为i[0…n-1]的位置删除元素

• insert(int i, const Type& value); //在第i个位置插入元素value

• clear(); //清空

查找遍历：

• visit(int i); // 在线性表中，查找位序为i的元素并返回其值

• search(const Type& value); //查找值为value的元素第一次出现的位序

• traverse(); //遍历

逆置：

• inverse(); // 逆置线性表

合并：

* Union(SeqList<Type>* lb); //两个单链表合并

3.代码实现

seqList.h

/**
 * @**Author: lwj**
 * @Date: 2022-05-28 13:04:41
 * @LastEditTime: 2022-05-28 13:04:41
 * @Description:数据结构---顺序表
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/seqList/seqList.h
 **/

#pragma once
#include <iostream>
#include <assert.h>

#define MAXSIZE 10
template <typename Type>
class SeqList
{
private:
    Type *data;  // 维护存储数据的指针
    int count;   // 记录元素个数
    int maxSize; // 数组容量
public:
    SeqList(int isSize = MAXSIZE);                   // 构造函数
    SeqList(const SeqList &s);                       // 拷贝构造
    ~SeqList() { delete[] data; }                    // 析构函数
    void clear() { count = 0; }                      // 清空表，只需修改count
    bool isEmpty() const { return count == 0; }      // 判空
    bool isFull() const { return count == maxSize; } // 判满
    int size() const { return count; }               // 返回顺序表的当前存储元素的个数
    void insert(int i, const Type &value);           // 在位置i上插入一个元素value，表的长度增1
    void remove(int i);                              // 删除位置i上的元素value，若删除位置合法，表的长度减1
    int search(const Type &value) const;             // 查找值为value的元素第一次出现的位序
    Type visit(int i) const;                         // 访问位序为i的元素值，“位序”0表示第一个元素，类似于数组下标
    void resize();                                   // 扩容
    void traverse() const;                           // 遍历顺序表
    void inverse();                                  // 逆置顺序表
    bool Union(SeqList<Type> &B);                    //合并两个表
};

template <typename Type>
SeqList<Type>::SeqList(int isSize) // 构造函数
{
    if (isSize < 0)
    {
        std::cout << "容量大小错误！" << std::endl;
        return;
    }
    this->maxSize = isSize;
    count = 0;
    data = new Type[maxSize]; //在堆区创建一个大小为maxSize的数组
}

template <typename Type>
SeqList<Type>::SeqList(const SeqList &s) // 拷贝构造
{
    maxSize = s.maxSize; // 也可以s有多少个元素就开辟多少空间
    count = s.count;
    data = new Type[maxSize];
    for (int i = 0; i < s.count; i++)
    {
        data[i] = s.data[i];
    }
}

template <typename Type>
void SeqList<Type>::insert(int i, const Type &value) // 在位置i上插入一个元素value，表的长度增1
{
    if (isEmpty())
    {
        cout << "已满！" << std::endl;
        return;
    }
    assert(i > 0 && i <= count); // i只能在[0~count]
    //在i处插入数据，i及其后面的元素向后移动一位
    for (int j = count; j > i; j--)
    {
        data[j] = data[j - 1];
    }
    data[i] = value;
    count++; //表长加一
}
template <typename Type>
void SeqList<Type>::remove(int i) // 删除位置i上的元素value，若删除位置合法，表的长度减1
{
    if (isEmpty())
    {
        std::cout << "为空！" << std::endl;
        return;
    }
    assert(i > 0 && i <= count - 1); // i只能在[0~count]
    for (int j = i; j <= count - 1; j--)
    {
        data[j] = data[j + 1]; //直接用后面一个数据覆盖所要删除的数据
    }
    count--; //表长减一
}
template <typename Type>
int SeqList<Type>::search(const Type &value) const // 查找值为value的元素第一次出现的位序
{
    for (int i = 0; i < count; i++)
        if (value == data[i])
            return i;
    return -1; // 查找失败返回-1
}
template <typename Type>
Type SeqList<Type>::visit(int i) const // 访问位序为i的元素值，“位序”0表示第一个元素，类似于数组下标
{
    assert(i > 0 && i <= count - 1); // i只能在[0~count-1]
    return data[i];
}
template <typename Type>
void SeqList<Type>::traverse() const // 遍历顺序表
{
    if (isEmpty())
    {
        std::cout << "数据为空！" << std::endl;
    }
    else
    {
        for (int i = 0; i < count; i++)
        {
            std::cout << data[i] << " ";
        }
        std::cout << std::endl;
    }
}
template <typename Type>
void SeqList<Type>::resize() // 扩容
{
    Type *tmp = new Type[2 * maxSize];
    for (int i = 0; i < count; i++)
    {
        tmp[i] = data[i];
    }
    delete[] data;
    data = tmp;
    tmp = nullptr;
    maxSize = 2 * maxSize;
}
template <typename Type>
void SeqList<Type>::inverse() // 逆置顺序表
{
    Type tmp;
    for (int i = 0; i < count / 2; i++)
    {
        tmp = data[i];
        data[i] = data[count - i - 1];
        data[count - i - 1] = tmp;
    }
}

//把B表合并到A表，如果A表和B表的元素递增有序排列，插入B表后A表还保持递增的次序
template <typename Type>
bool SeqList<Type>::Union(SeqList<Type> &B)
{
    int m, n, k, i, j;
    m = this->count;              // 当前对象为线性表A
    n = B.count;                  // m，n分别为线性表A和B的长度
    k = m + n - 1;                // k为结果线性表的工作指针（下标）
    i = m - 1, j = n - 1;         // i，j分别为线性表A和B的工作指针（下标）
    while (m + n > this->maxSize) // 空间不够，扩大表空间到够为止
    {
        resize();
    }
    //下面的操作就是排序
    while (i >= 0 && j >= 0) // 合并顺序表，直到一个表为空
    {
        if (data[i] >= B.data[j]) //如果A的元素大于B的元素时
        {
            data[k--] = data[i--]; // A表下标为k元素等于下标为i的元素
        }
        else
        {
            data[k--] = B.data[j--]; // 默认当前对象，this指针可省略
        }
    }
    while (j >= 0) // 将B表的剩余元素复制到A表
    {
        data[k--] = B.data[j--];
    }
    count = m + n; // 修改A表长度
    return true;
}

main.cpp

/**
 * @Author: lwj
 * @Date: 2022-05-28 13:04:14
 * @LastEditTime: 2022-05-28 13:04:14
 * @Description:测试顺序表
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/main.cpp
 **/
#include "seqList.h"
using namespace std;

void testSeqList()
{
    SeqList<int> s1;
    SeqList<int> s2;

    cout << "insert插入测试：" << endl;
    for (int i = 0; i < 10; i++)
    {
        s1.insert(i, i);
        s2.insert(i, 99);
    }
    s1.traverse();

    cout << "测试返回表大小函数size（）：" << s1.size() << endl;

    cout << "拷贝构造函数测试：" << endl;
    SeqList<int> s3(s1);
    s3.traverse();

    cout << "表满扩大容量函数resize():" << endl;
    cout << "未扩大表时的容量：" << s1.size() << endl;
    for (int i = 0; i < 10; i++)
    {
        if (s1.isFull())
        {
            s1.resize();
        }
        s1.insert(0, 88);
    }
    cout << "扩大表后容量为：" << s1.size() << endl;
    s1.traverse();

    cout << "测试删除元素函数remove()：" << endl;
    s1.remove(s1.size()); //删除最后一个元素
    s1.traverse();

    cout << "测试visit()功能：" << s1.visit(5) << endl;

    cout << "测试查找value元素功能：" << s1.search(4) << " "
         << s1.search(99) << endl;

    cout << "测试逆置功能：" << endl;
    s1.inverse();
    s1.traverse();

    cout << "测试s3表插入s2表：" << endl;
    s2.clear();
    for (int i = 0; i < 10; i++)
    {
        s2.insert(i, i+4);
    }
    s2.Union(s3);
    s2.traverse();
}
int main()
{
    testSeqList();
    return 0;
}

二、单链表

顺序栈是使用数组存储方式的栈

说明一个问题，链表可以没有头结点，不影响链表的基本功能，更细节问题请自行百度，而我下面的代码实现的链表都有头结点。

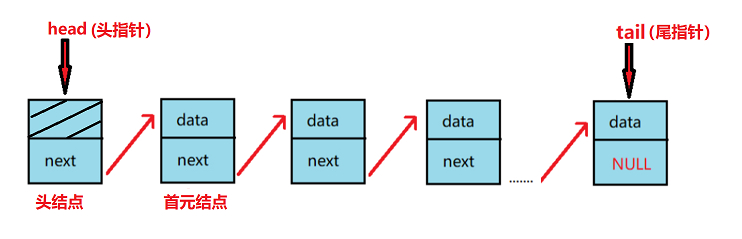
1.结构模型图

2.单链表的常用接口

功能描述：单链表容器常用的对外接口

构造函数：

• LinkList(); //构造函数

数据存取：

• push_front(); // “头插法”创建单
• push_back(); // “尾插法”创建单链表

大小操作：

• isEmpty(); //判断顺序表是否为空
• size(); //返回栈的大小

插入删除：

• remove(int i); //在线性表中，位序为i[0…n-1]的位置删除元素

• insert(int i, const Type& value); //在第i个位置插入元素value

• clear(); //清空

查找遍历：

• visit(int i); // 在线性表中，查找位序为i的元素并返回其值

• search(const Type& value); //查找值为value的元素第一次出现的位序

• traverse(); //遍历

逆置：

* inverse(); // 逆置线性表

3.代码实现

linkList.h

/**
 * @Author: lwj
 * @Date: 2022-05-29 16:04:26
 * @Description:实现单链表
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/LinkList/LinkList.h
 **/
#pragma once
#include <iostream>
#include <assert.h>

template <typename Type>
class LinkList //单链表
{
private:
    //这里我用结构体来做结点，也可以在LinkList类外在创建一个类实现，
    //类实现的话用到友元类，有兴趣的可以自己实现一下
    struct Node
    {
    public:
        Type data;                                //数据域
        Node *next;                               //指针域
        Node(const Type value, Node *p = nullptr) //结构体Node的两个参数的构造函数
        {
            this->data = value;
            this->next = p;
        }
        Node(Node *p = nullptr) //一个参数的构造函数,用创建头结点之类的使用
        {
            this->next = p;
        }
    };
    Node *head;                  //头指针
    Node *tail;                  //尾指针
    int count;                   //元素个数
    Node *getIndex(int i) const; //返回指向第i个元素的指针

public:
    LinkList();                                          //构造函数
    ~LinkList();                                         //析构函数
    bool empty() const { return head->next == nullptr; } //判空
    void clear();                                        //清空单链表
    int size() const { return count; }                   //返回元素个数
    void insert(int i, const Type &value);               //在第i个位置插入value
    void remove(int i);                                  //删除第i个元素
    int search(const Type &value) const;                 //查找value第一次出现的下标
    void traverse() const;                               //遍历
    Type visit(int i) const;                             // 在线性表中，查找位序为i的元素并返回其值
    void push_front();                                   // “头插法”创建单链表
    void push_back();                                    // “尾插法”创建单链表
    void inverse();                                      // 逆置线性表

};

template <typename Type>
LinkList<Type>::LinkList() //构造函数
{
    head = tail = new Node(); //创建一个空表，只有头结点，如果不需要头结点的话直接head=tail=nullptr;
    this->count = 0;
}

template <typename Type>
LinkList<Type>::~LinkList() //析构函数
{
    clear();
    delete head;
}

template <typename Type>
void LinkList<Type>::clear() //清空单链表，clear()和~LinkList()在于，clear()保留头结点
{
    Node *p, *tmp;
    p = head->next; // head->next指向首元结点
    while (p != nullptr)
    {
        tmp = p;
        p = p->next;
        delete tmp;
    }
    head->next = nullptr;
    tail = head;
    count = 0;
}
//
template <typename Type>
typename LinkList<Type>::Node *LinkList<Type>::getIndex(int i) const //返回指向第i个元素的指针
{
    Node *p = head;
    if (i < -1 || i > this->count - 1)
        return nullptr;

    int num = 0;
    while (num <= i)
    {
        p = p->next;
        num++;
    }
    return p;
}

template <typename Type>
void LinkList<Type>::insert(int i, const Type &value) //在第i个位置插入value
{
    if (i < 0 || i > this->count) //能插入的位置i的范围[0~cout]
    {
        std::cout << "outOfRange!" << std::endl;
        return;
    }
    Node *p = this->getIndex(i - 1);    // p指向原来i结点的元素
    Node *q = new Node(value, p->next); // q指向新插入的元素
    p->next = q;                        // p->next指向新插入的元素
    if (p == tail)
    {
        tail = q;
    }
    this->count++;
}

template <typename Type>
void LinkList<Type>::remove(int i) //删除第i个元素
{
    Node *pre, *p;
    if (i < 0 || i > this->count - 1) //只有在[0~count-1]范围内有data
    {
        std::cout << "outOfRange!" << std::endl;
        return;
    }
    pre = this->getIndex(i - 1); //返回指向的结点的指针
    p = pre->next;
    if (p == tail) //当删除的是尾结点时，让倒数第二个结点成为尾结点，尾指针指向它
    {
        tail = pre;
        pre->next = nullptr;
        delete p;
    }
    else
    {
        pre->next = p->next;
        delete p;
        this->count--;
    }
}

template <typename Type>
int LinkList<Type>::search(const Type &value) const //查找value第一次出现的下标
{
    Node *p = head->next;
    int num = -1;
    while (p != nullptr && p->data != value)
    {
        p = p->next;
        num++;
    }
    if (p->next == nullptr)
    {
        return -1;
    }
    else
    {
        return num;
    }
}

template <typename Type>
void LinkList<Type>::traverse() const //遍历单链表
{
    Node *p = head->next;
    cout << "traverse：" << endl;
    while (p != nullptr)
    {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}

template <typename Type>
Type LinkList<Type>::visit(int i) const // 在线性表中，查找位序为i的元素并返回其值
{
    Node *p = head->next;
    int num = 0;
    if (i < 0 || i > this->count - 1)
    {
        std::cout << "outOfRange!" << std::endl;
        assert(1);
    }
    while (i > num)
    {
        p = p->next;
        num++;
    }
    return p->data;
}

template <typename Type>
void LinkList<Type>::push_front() // “头插法”创建单链表,从首元结点开始插入
{
    Node *p = nullptr;
    Type value, flag;
    cout << "请输入结束标志flag的值:";
    cin >> flag;
    while (cin >> value, value != flag)
    {
        // cin>>value;
        // if(value==flag)
        // {
        //     break;
        // }
        p = new Node(value, head->next);
        head->next = p;
        if (head == tail) //成立说明表为空，此时头指针和尾指针现在都指向头结点，
        {
            tail = p;
        }
        count++;
    }
}

template <typename Type>
void LinkList<Type>::push_back() //尾插法
{
    Node *p;
    int value, flag;
    cin >> flag;

    while (cin >> value, flag != value)
    {
        p = new Node(value, nullptr);
        tail->next = p;
        tail = p;
        count++;
    }
}
//逆置单链表思路，先用头指针和头结点构建一个空表，然后把其它结点反着插入空表，参考一下头插法
template <typename Type>
void LinkList<Type>::inverse() // 逆置线性表
{
    Node *p, *tmp;
    p = head->next;       // 工作指针p记录首元结点位置
    head->next = nullptr; //让头结点的next指向空，构成空表
    if (p)                //如果p为空，说明表为空
    {
        tail = p;
    }
    while (p) //不为空表时
    {
        tmp = p->next;        // 指向旧首元结点的后继（下一个）
        p->next = head->next; // p->next指向头结点的next指向的位置
        head->next = p;       // 然后头结点的next指向刚插入的结点
        p = tmp;              //工作指针p重新指向其它未插入结点的开始位置
    }
}

main.cpp

/**
 * @Author: lwj
 * @Date: 2022-05-29 16:04:33
 * @Description:测试单链表
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/linkList/main.cpp
 **/
#include <iostream>
using namespace std;
#include "linkList.h"

void testlinkList()
{
    LinkList<int> L1;
    LinkList<int> L2;

    cout << "插入测试：" << endl;
    for (int i = 0; i < 4; i++)
    {
        L1.insert(i, i);
        L2.insert(i, i);
    }

    // cout << "测试插入操作：" << endl;
    // L1.insert(2, 99);
    // L1.traverse();

    // cout << "测试判空和返回单链表大小：" << endl;
    // if (L1.empty())
    // {
    //     cout << "单链表为空！" << endl;
    // }
    // else
    // {
    //     cout << "单链表不为空,其大小为：" << L1.size() << endl;
    // }

    // cout << "测试删除功能：" << endl;
    // L1.remove(2);
    // L1.traverse();

    // cout << "测试查找位序为2的元素的值：" << endl;
    // L1.clear();
    // cout << L1.visit(2) << endl;

    // // cout << "头插法测试：" << endl;
    // // L1.push_front();
    // // L1.traverse();
    // cout << "测试逆置操作：" << endl;
    // L1.inverse();
    // L1.traverse();

    cout << "测试两个单链表合并操作：" << endl;
    L1.Union(&L2);
    L1.traverse();
    L2.traverse();
}

int main()
{

    testlinkList(); //单链表测试
    return 0;
}

三、双链表

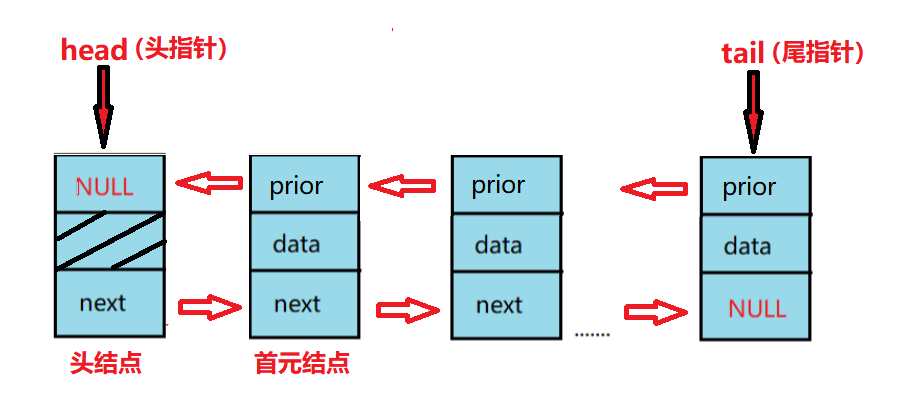
1.结构模型图

2.双链表的常用接口

功能描述：双链表容器常用的对外接口

构造函数：

• doubleLinkList(); //构造函数

数据存取：

• push_front(); // “头插法”创建单
• push_back(); // “尾插法”创建单链表

大小操作：

• isEmpty(); //判断顺序表是否为空
• size(); //返回栈的大小

插入删除：

• remove(int i); //在线性表中，位序为i[0…n-1]的位置删除元素

• insert(int i, const Type& value); //在第i个位置插入元素value

• clear(); //清空

查找遍历：

• visit(int i); // 在线性表中，查找位序为i的元素并返回其值

• search(const Type& value); //查找值为value的元素第一次出现的位序

• traverse(); //遍历

逆置：

• inverse(); // 逆置线性表

3.代码实现

doubleLinkList.h

/**
 * @Author: lwj
 * @Date: 2022-05-30 23:42:24
 * @Description:实现双链表
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/dobleLinkList/DoubleLinkList.h
 **/
#pragma once
template <typename Type>
class DoubleLinkList
{
private:
    struct Node
    {
    public:
        Type data;   //数据域
        Node *next;  //指向后继结点
        Node *prior; //指向前继结点
        Node(Node *p, const Type &value, Node *n)
        {
            this->data = value;
            this->next = n;
            this->prior = p;
        }
        Node() : prior(NULL), next(NULL) {} //用列表初始化方法初始化
        ~Node() {}
    };
    Node *head, *tail;
    int count;
    Node *getIndex(int i) const; //返回第i元素的前驱
public:
    DoubleLinkList();                                 //构造函数
    ~DoubleLinkList();                                //析构函数
    bool empty() const { return head->next == tail; } //判空
    Type size() const { return count; }               //返回
    void clear();                                     //清空
    void insert(int i, const Type &value);            //在第i个位置插入元素value
    int search(const Type &value) const;              //在线性表中，查找值为value的元素第一次出现的位序
    void traverse() const;                            //遍历双链表
    Type visit(int i) const;                          // 在线性表中，查找位序为i的元素并返回其值
    void remove(int i);                               //在线性表中，位序为i[0..n-1]的位置删除元素
    virtual void inverse();                           // 逆置线性表
};

template <typename Type>
DoubleLinkList<Type>::DoubleLinkList() //构造函数
{
    //有两个头结点，头指针和尾指针处各有一个
    head = new Node; //头部头结点
    tail = new Node; //尾部头结点
    head->next = tail;
    tail->prior = head;
    count = 0;
}

template <typename Type>
void DoubleLinkList<Type>::clear() //清空
{
    Node *p = head->next;
    Node *tmp;
    head->next = tail;
    tail->prior = head;
    while (p != tail)
    {
        tmp = p->next;
        delete p;
        p = tmp;
    }
    count = 0;
}

template <typename Type>
DoubleLinkList<Type>::~DoubleLinkList() //析构函数
{
    clear();
    delete head;
    delete tail;
}

template <typename Type>
typename DoubleLinkList<Type>::Node *DoubleLinkList<Type>::getIndex(int i) const //返回指向第i个元素的指针
{
    Node *p = head;
    int m = 0;
    if (i < -1 || i > this->count)
    {
        return nullptr;
    }

    while (m <= i)
    {
        p = p->next;
        m++;
    }
    return p;
}

template <typename Type>
void DoubleLinkList<Type>::insert(int i, const Type &value)
{
    Node *p, *tmp;
    if (i < 0 || i > count) // 合法的插入位置为[0..n]
    {
        std::cout << "outOfRange!" << std::endl;
        return;
    }
    p = getIndex(i);                    // 若i==n则定位到tail指向的尾结点
    tmp = new Node(p->prior, value, p); // tmp插入到p之前
    p->prior->next = tmp;
    p->prior = tmp;
    ++count;
}

template <typename Type>
void DoubleLinkList<Type>::remove(int i) // 在线性表中，位序为i[0..n-1]的位置删除元素
{
    Node *p;
    if (i < 0 || i > count - 1)
    {
        std::cout << "outOfRange!" << std::endl;
        return;
    }

    p = getIndex(i);
    p->prior->next = p->next;  //将i结点的前继的next指向i结点的后继
    p->next->prior = p->prior; //将i结点的后继的prior指向i结点的前继
    delete p;                  //删除i结点
    --count;
}

template <typename Type>
void DoubleLinkList<Type>::traverse() const //遍历双链表
{
    Node *p;
    p = head->next;
    std::cout << "遍历双链表：";

    while (p != tail)
    {
        std::cout << p->data << " ";
        p = p->next;
    }
    std::cout << std::endl;
}
template <typename Type>
int DoubleLinkList<Type>::search(const Type &value) const //在线性表中，查找值为value的元素第一次出现的位序
{
    Node *p = head->next;
    int num = 0;
    while (num <= count - 1 && p != tail)
    {
        if (value == p->data)
        {
            return num;
        }
        p = p->next;
        ++num;
    }
}

template <typename Type>
Type DoubleLinkList<Type>::visit(int i) const // 在线性表中，查找位序为i的元素并返回其值
{
    if (i < 0 || i > this->count - 1)
    {
        std::cout << "outOfRange!" << std::endl;
        return -1; //找不到
    }

    Node *p = this->getIndex(i);
    return p->data;
}

template <typename Type>
void DoubleLinkList<Type>::inverse() // 逆置线性表
{
    Node *p = head->next;
    Node *tmp;
    head->next = tail;
    tail->prior = head;
    while (p != tail)
    {
        tmp = p->next;
        p->next = head->next;
        p->prior = head;
        head->next->prior = p;
        head->next = p;
        p = tmp;
    }
}

main.cpp

/**
 * @Author: lwj
 * @Date: 2022-05-30 23:47:19
 * @Description:测试双链表功能
 * @FilePath: /Linux_C_C-plus-plus/数据结构（C++）/list/dobleLinkList/main.cpp
 **/

#include <iostream>
#include "doubleLinkList.h"
using namespace std;
void DoubleLinkList_test()
{
    DoubleLinkList<int> d1;

    for (int i = 0; i < 4; i++)
    {
        d1.insert(i, i);
    }
    cout << "判空和返回大小测试：" << endl;
    if (d1.empty())
    {
        cout << "双链表为空！" << endl;
    }
    else
    {
        cout << d1.size() << endl;
    }
    d1.traverse();

    cout << "删除函数remove()的测试：" << endl;
    d1.remove(0);
    d1.remove(3);
    d1.traverse();

    cout << "search()函数的测试：" << endl;
    cout << "元素3第一次出现的位序为：" << d1.search(3) << endl;

    // cout << "测试逆置功能：" << endl;
    // d1.inverse();
    // d1.traverse();
}
int main()
{
    DoubleLinkList_test(); //双链表测试
    return 0;
}

四、总结

1.数组

所申请的内存空间，必须是线性连续，且申请的空间大小必须提前确定。

插入和删除操作代价比较大，需要该位置后面的数据都向后移动，留出一个空位进行插入，或者都向前移动，把该空位的数据进行覆盖（也就是删除）；

查询代价较小，数组是连续存储的，知道该数组名称，可根据下标直接查询；

不利于扩展，数组空间是提前申请的，当存储空间不够时，需要重新申请空间。

2. 链表

申请内存中存储空间，不要求连续，只需要保存下一个存储空间的内存地址即可。

插入和删除操作比较容易，只需要改变指针的指向即可；

查询代价较大，不具备随机访问能力，需要从头到尾遍历查找；

扩展性较好，不用提前指定大小，插入删除比较随意。