数据结构(链表)(1)

这节先大概理解一下链表的结构.

为啥会出现链表这东西呢? 这个问题已经在数据结构的前言, 也就是第一节讲过了.
那么现在再来详细的通过顺序表和链表的对比告诉大家为啥需要那么多的数据结构:

顺序表的问题:
头部和中间插入元素数据的效率都不行, 时间复杂度都是O(N). 因为都需要通过挪动旧数据, 空出位置给新的数据, 效率低.
空间不足够的时候, 扩容有一定的消耗(尤其是异地扩容). 扩容分类的问题在“顺序表(1)”中的判断空间是否足够的那个函数的底下有介绍.
异地扩容就像一家公司出去团建租酒店, 一开始只有5个人, 后来又多来了5个人, 公司要求酒店说, 我们的员工的房间得是连续的连在一起的, 相邻的. 这时候, 如果说原本的5个房间的周围恰好有5个房间符合要求的话, 就直接让新来的员工住进去了.
但是要是原本的房间周围没有符合要求的房间, 酒店就需要先去酒店的系统查看, 有没有符合要求的连续的10个房间, 然后再让原本的5个员工退房, 然后再让这10个人重新到新的一块的区域住下.
所以这个扩容其实对系统的消耗是很大的, 当插入的数据多了一些之后, 大部分的扩容都会是异地扩容. 所以说这是一个比较严重的问题.

其次, 顺序表的扩容逻辑比较简单单一, 一般来说一次扩容就是成倍扩容, 这就很有可能造成很大的空间消耗.
就好比如本来顺序表的容量是100, 而且现在已经有了100个有效数据了, 现在你要再插入10个数据进来, 那么扩容一次, 就直接干到了200, 那么剩下的90个空间的位置就被浪费了.

当然, 顺序表也是有优点的:
尾部插入和尾部删除都足够快, 足够简单.
顺序表其实差不多就是一个数组, 由于数组的下标, 可以让我们更好的去访问到各个数据, 并且能对数据进行一个修改. 这就是数组下标带来的优越性.

那么既然顺序表不够完美, 那么就必然会有新的数据结构, 那么就有人整出了一个新的数据结构”链表”.
链表相较于顺序表, 复杂层度上有一些的提高, 但是个人认为还是比较好的去理解的.
链表一共有8个形态, 大方向上主要是分为:
单向链表
双向链表

其余的就是是否循环, 是否带头, 然后相互组合. 本节先讲最基础的一个, “单向不循环链表”.
咱们可以先通过画图来了解一下顺序表和链表之间的一个结构差异, 和一些不同之处.

请添加图片描述

为了大家能更好的理解, 这里也简单手搓出一个简单的链表结构, 然后打印一个链表给大家看看, 让大家知道一下, 怎么遍历链表, 链表结构是啥样的. 这个不是正式的代码, 仅是做个演示.

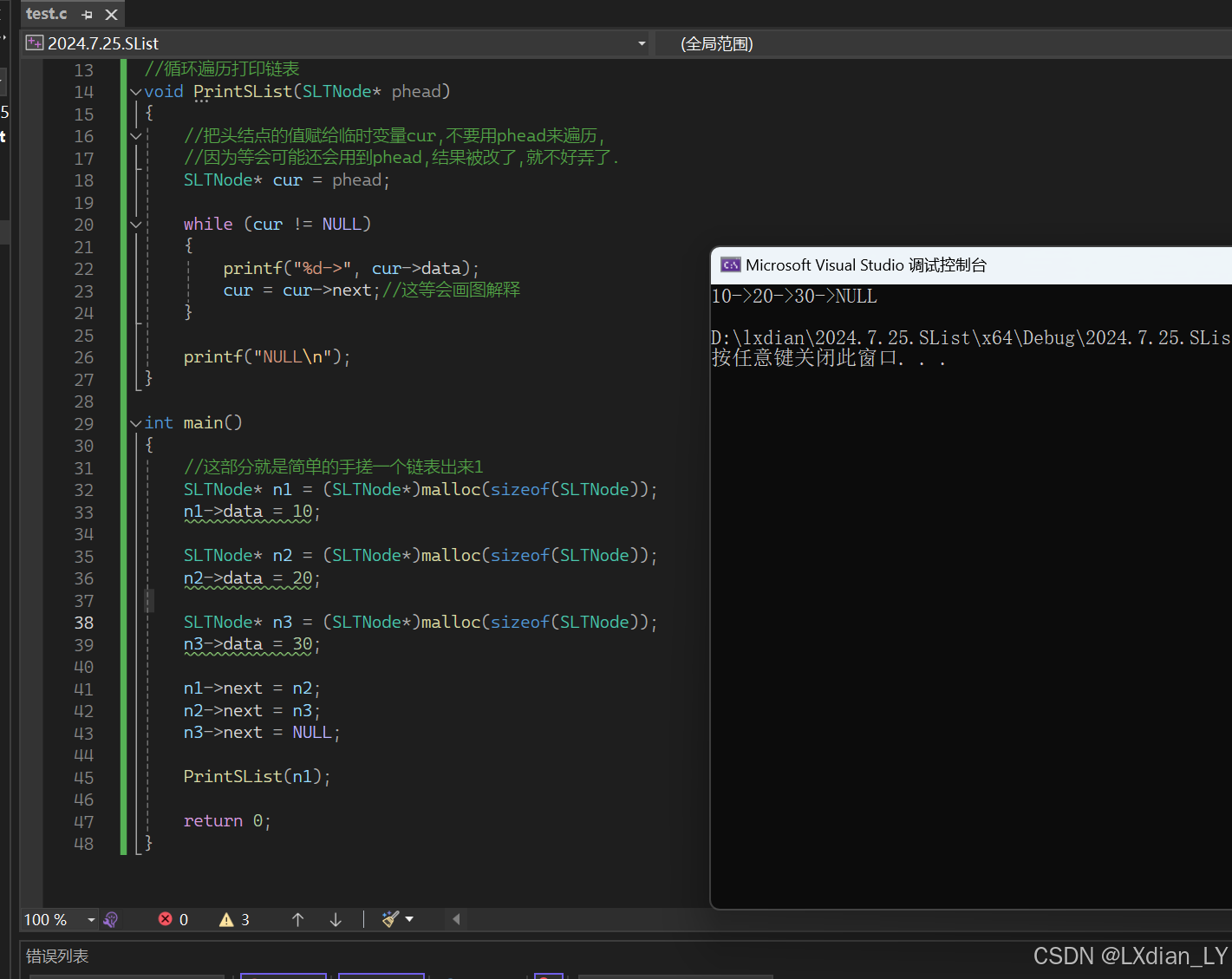
#include<stdio.h>
#include<stdlib.h>

typedef int SLDatatype;
//链表节点的结构:
typedef struct SListNode
{
	SLDatatype data;
	struct SListNode* next;

}SLTNode;

//循环遍历打印链表
void PrintSList(SLTNode* phead)
{
	//把头结点的值赋给临时变量cur,不要用phead来遍历,
	//因为等会可能还会用到phead,结果被改了,就不好弄了.
	SLTNode* cur = phead;

	while (cur != NULL)
	{
		printf("%d->", cur->data);
		cur = cur->next;//这等会画图解释
	}

	printf("NULL\n");
}

int main()
{
	//这部分就是简单的手搓一个链表出来1
	SLTNode* n1 = (SLTNode*)malloc(sizeof(SLTNode));
	n1->data = 10;

	SLTNode* n2 = (SLTNode*)malloc(sizeof(SLTNode));
	n2->data = 20;

	SLTNode* n3 = (SLTNode*)malloc(sizeof(SLTNode));
	n3->data = 30;

	n1->next = n2;
	n2->next = n3;
	n3->next = NULL;

	PrintSList(n1);

	return 0;
}

请添加图片描述

这就是代码下, 链表的结构.

然后解释一下打印函数是怎么遍历链表的

请添加图片描述

这节先讲这些, 下节将正式开始链表.

数据结构(链表)(1)

数据结构(链表)(1)

悦读