目录
一、ResNet诞生背景
深度残差网络(deep residual network)是2015年微软何凯明团队发表的一篇名为:《Deep Residual Learning for Image Recognition》的论文中提出的一种全新的网络结构,其核心模块是残差块residual block。正是由于残差块结构的出现使得深度神经网络模型的层数可以不断加深到100 层、1000层甚至更深,从而使得该团队在当年的ILSVRC 2015分类竞赛中取得卓越成绩,也深刻地影响了以后的很多深度神经网络的结构设计。 残差网络的成功不仅表现在其在ILSVRC 2015竞赛中的卓越效果,更是因为残差块skip connection/shorcut这样优秀的思想和设计,使得卷积网络随着层数加深而导致的模型退化问题能被够大幅解决,使模型深度提高一个数量级,到达上百、上千层。
1.核心特点
-
残差块(Residual Block):
-
学习残差函数 F(x)=H(x)−x,通过跳跃连接将输入 x 加到输出上:H(x)=F(x)+x。
-
跳跃连接缓解了梯度消失问题,使深层网络更容易训练。
-
-
结构:
-
基本残差块:2-3个卷积层 + 跳跃连接。
-
更深版本(如ResNet-50)使用“瓶颈结构”(1x1卷积减少计算量)。
-
-
变体:
-
ResNet-18、ResNet-34(基本残差块)。
-
ResNet-50、ResNet-101、ResNet-152(瓶颈结构)。
-
-
应用:
-
图像分类、目标检测、语义分割等任务中表现优异。
-
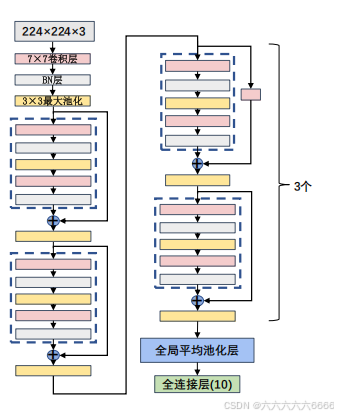
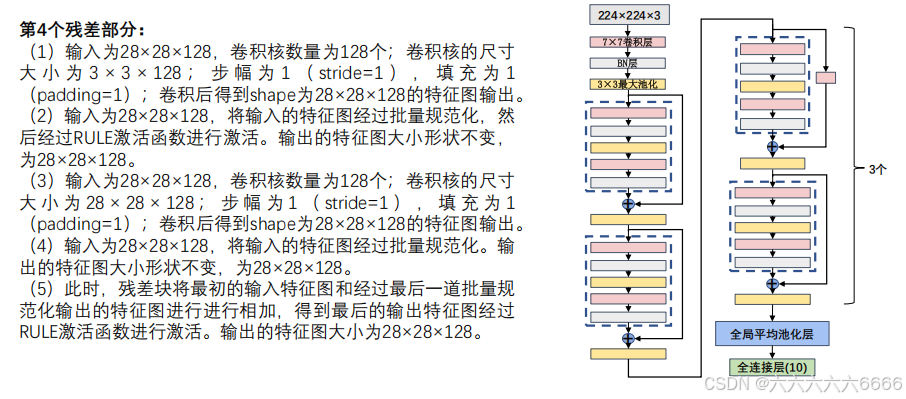
具体结构如下:
二、网络加深带来的问题
在残差块这样的结构引入之前,如果一个神经网络模型的深度太深,可能会带来梯度消失和梯度爆炸的问题 (如下图),随着一些正则化方法的应用可以缓解此问题,但是随着layer深度的继续加深,又带来了模型退化这样的问题。
那么,这里就有一个问题,为什么加深网络会带来退化问题?即使新增的这些layer什么都没学习,保持恒等输出(所有的weight都设为1),那么按理说网络的精度也应该等于原有未加深时的水平,如果新增的layer学习到了有用特征,那么必然加深过后的模型精度会大于未加深的原网络。看起来对于网络的精度加深后都应该大于等于加深前才对啊?实际上,让新增的layer保持什么都不学习的恒等状态,恰恰很困难,因为在训练过程中每一层layer都通过线性修正单元relu处理,而这样的处理方式必然带来特征的信息损失(不论是有效特征or冗余特征)。所以上述假设的前提是不成立的,简单的堆叠layer必然会带来退化问题。
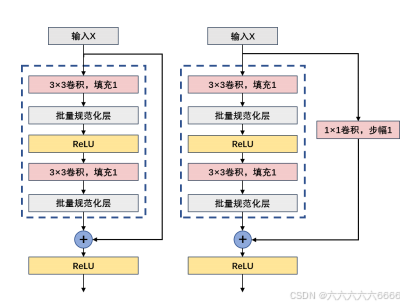
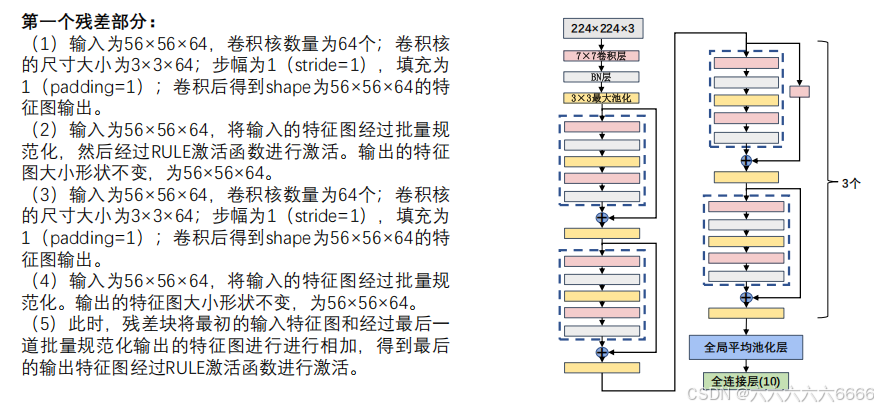
三、ResNet的基础架构----残差块
ResNet的基础架构–残差块(residual block)。在残差块中,输入可通过跨层数据线路更快地向
前传播。
ResNet沿用了VGG完整的3×3卷积层设计。残差块里首先有2个有相同输出通道数的3×3卷积
层。每个卷积层后接一个批量规范化层和ReLU激活函数。然后我们通过跨层数据通路,跳过这
2个卷积运算,将输入直接加在最后的ReLU激活函数前。这样的设计要求2个卷积层的输出与输
入形状一样,从而使它们可以相加。如果想改变通道数,就需要引入一个额外的1×1卷积层来将
输入变换成需要的形状后再做相加运算。
第一种类型:
第二种类型:
注意:图中最右侧的1 x 1的作用是改变通道数的
四、 Batch Normalization
BN是由Google于2015年提出,这是一个深度神经训练的技巧,它不仅可以加快了模型的收敛速度,使训练深层网络模型更加容易和稳定。目前BN已经成为几乎所有卷积神经网络的标配技巧了。
从字面意思看来Batch Normalization(简称BN) 就是对每一批数据进行归一化,确实如此,对于训练中某一个batch的数据{x1,x2,...,xn},注意这个数据是可以输入也可以是网络中间的某一层输出。在BN出现之前,我们的归一化操作一般都在数据输入层,对输入的数据进行求均值以及求方差做归一化,但是BN的出现打破了这一个规定,我们可以在网络中任意一层进行归一化处理,因为我们现在所用的优化方法大多都是min-batch SGD,所以我们的归一化操作就成为Batch Normalization。
注意:归一化就是0到1之间,标准化是按照自己的要求来规定,归一化是标准化的一种
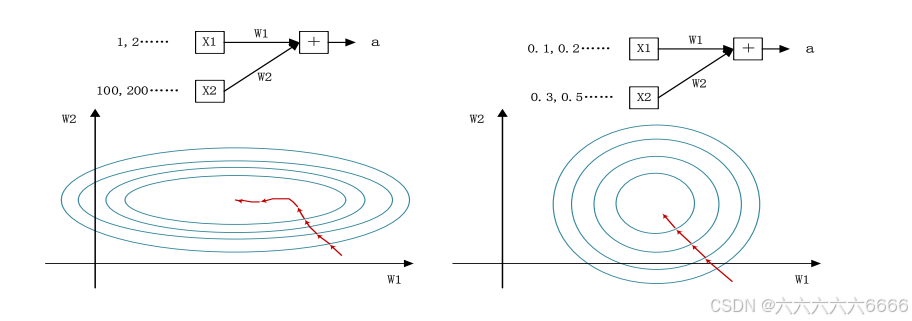
1.为什么要归一化
我们知道网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。
以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。BN的提出,就是要解决在训练过程中,中间层数据分布发生改变的情况。
2.BN怎么做
如下图所示,BN步骤主要分为4步:
(1)求每一个训练批次数据的均值
(2)求每一个训练批次数据的方差
(3)使用求得的均值和方差对该批次的训练数据做归一化,获得0-1分布。其中ε是为了避免除数
为0时所使用的微小正数。
(4)尺度变换和偏移:将xi乘以γ调整数值大小,再加上β增加偏移后得到yi,这里的γ是尺度因子,β是平移因子。这一步是BN的精髓,由于归一化后的xi基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数: γ,β。γ和β是在训练时网络自己学习得到的。
3.BN解决的问题
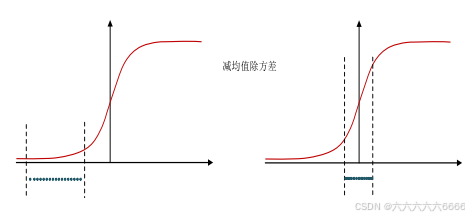
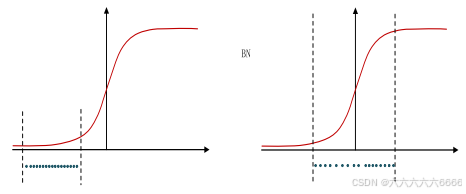
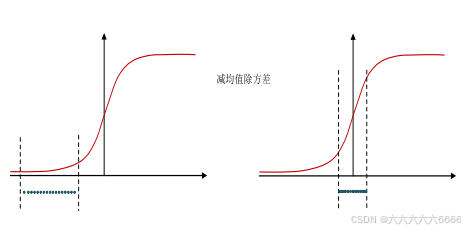
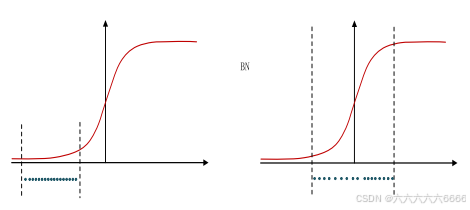
(1)减均值除方差后,数据就被移到中心区域,对于大多数激活函数而言,这个区域的梯度都是最大的或者是有梯度的这可以看做是一种对抗梯度消失的有效手段。如果对于每一层数据都那么做的话,数据的分布总是在随着变化敏感的区域,相当于不用考虑数据分布变化了,这样训练起来更有效率。
(2)那么为什么要有第4步,不是仅使用减均值除方差操作就能获得目的效果吗?我们思考一个问题,减均值除方差得到的分布是正态分布,我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢?
(3)不能,比如数据本身就很不对称,或者激活函数未必是对方差为1的数据最好的效果,比如 Sigmoid激活函数,在-1~1之间的梯度变化(注意是变化,而不是这块的值大不大,线性一次函数的梯度是一个定值)不大,那么非线性变换的作用就不能很好的体现,换言之就是,减均值除方差操作后可能会削弱网络的性能!针对该情况,在前面三步之后加入第4步完成真正的batch normalization 。
(4)BN的本质就是利用优化变一下方差大小和均值位置,使得新的分布更切合数据的真实分布,
保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
4.BN 层总结
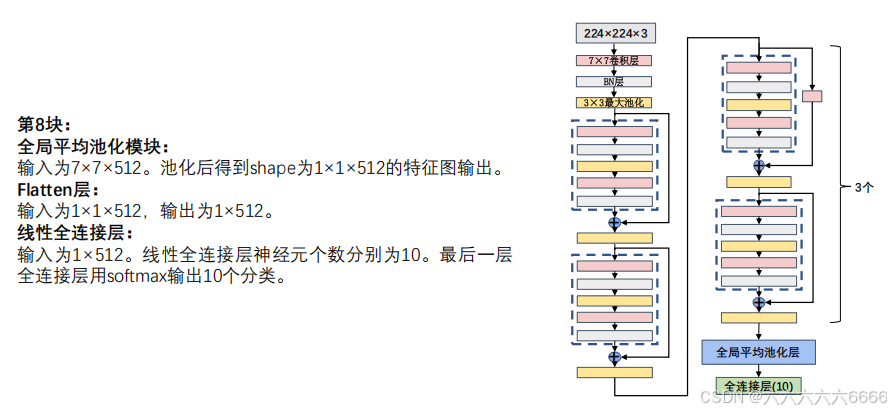
五、ResNet 网络参数详解
六、ResNet 总结
残差网络的出现使人们摆脱了深度的束缚,大幅改善了深度神经网络中的模型退化问题,使网络层数从数十层跃升至几百上千层,大幅提高了模型精度,通用性强适合各种类型的数据集和任务。残差块和shortcut这种优秀的设计也极大影响了后面的网络结构发展。