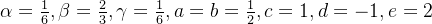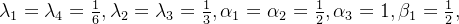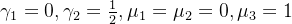常微分方程算法之龙格-库塔法（Runge-Kutta法）

一、方法背景

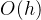
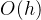
在常微分方程算法之欧拉法中我们提到，通过数值计算求解连续问题的基本思想是采用离散化方法将连续问题转化为离散问题，进而采用迭代的方式求解差分格式的离散方程。在从离散方程到差分方程的过程中，我们采用了将高阶项 O(h) 忽略的近似方法， O(h) 称为局部截断误差。而对于一阶常微分方程来说，如果其精确解在求解域I上存在k+1阶连续导数，则利用泰勒级数展开可得：

$y(x_{i+1})=y(x_{i})+hy^{'}(x_{i})+\frac{h^{2}}{2!}y^{''}(x_{i})+\cdot \cdot \cdot +\frac{h^{k}}{k!}y^{(k)}(x_{i})+O(h^{k+1}) \space\space\space\space (1)$

如果忽略式（1）中的高阶项 $O(h^{k+1})$ ，可得：

$y_{i+1}=y_{i}+hy^{'}_{i}+\frac{h^{2}}{2!}y^{''}_{i}+\cdot\cdot\cdot+\frac{h^{k}}{k!}y^{(k)}_{i} \space\space\space\space (2)$

如果令式（2）中k=1，即可获得欧拉法，所以本质上欧拉法是一阶泰勒级数方法的数值计算，称之为一阶方法。如果令k=2，并忽略高阶项，可得二阶泰勒级数数值计算公式：

$y_{i+1}=y_{i}+hf(x_{i},y_{i})+\frac{h^{2}}{2!}(f_{x}(x_{i},y_{i})+f(x_{i},y_{i})f_{y}(x_{i},y_{i})) \space\space\space\space (3)$

由梯形法和改进欧拉法可知，两者均属于二阶方法。故阶数越高，计算精度越高，也即可以通过控制局部截断误差来提升算法精度。

二、算法原理及推导过程

1、二阶龙格-库塔公式

对改进欧拉法差分格式进行推导变形：

$y_{i+1}=y_{i}+\frac{1}{2}h[f(x_{i},y_{i})+f(x_{i+1},y_{i+1})] \\ \space\space\space\space =y_{i}+\frac{1}{2}h[f(x_{i},y_{i})+f(x_{i}+h,y_{i}+hf(x_{i},y_{i})]\\ \space\space\space\space =y_{i}+hy^{'}(x_{i})+\frac{h^{2}}{2}y^{'}(x_{i})+O(h^{3})$

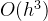
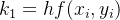
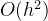
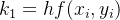
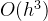
由此可见，改进欧拉法本质上与泰勒级数二阶展开（公式3）只差一项 $O(h^{3})$ 。所以，泰勒级数展开中各阶导数可以用函数在一些点上值的线性组合近似地表示。对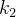于欧拉法， $y_{(i+1)}=y_{i}+k_{1}$ ，其中 $k_{1}=hf(x_{i},y_{i})$ ，局部截断误差为 $O(h^{2})$ ；对于改进欧拉法， $y_{(i+1)}=y_{i}+\frac{1}{2}(k_{1}+k_{2})$ ，其中 $k_{1}=hf(x_{i},y_{i})$ ， $k_{2}=hf(x_{i}+h,y_{i}+k_{1})$ ，局部截断误差为 $O(h^{3})$ 。将二阶泰勒级数数值格式写成一般格式：

$\left\{\begin{matrix} y_{i+1}=y_{i}+\alpha k_{1}+\beta k_{2}\\ k_{1}=hf(x_{i},y_{i}) \;\;\; (4)\\ k_{2}=hf(x_{i}+ah,y_{i}+bk_{1}) \end{matrix}\right.$

对 $k_{2}$ 进行二元函数泰勒展开：

$k_{2}=hf(x_{i}+ah,y_{i}+bk_{1})=hf(x_{i}+ah,y_{i}+bhf)$

$k_{2}=h[f+ahf_{x}+bhff_{y}+\frac{1}{2}(a^{2}h^{2}f_{xx}+2abh^{2}ff_{xy}+b^{2}h^{2}f^{2}f_{yy})]+O(h^{4})$

则公式（4）可以写作：

$y_{i+1}=y_{i}+(\alpha +\beta)hf+h^{2}\beta (af_{x}+bff_{y})+O(h^{3}) \space\space\space\space (5)$

将公式（5）与公式（3）比较可知，只要满足，两式则对等：

$\alpha+ \beta=1,\space\space a\beta=b\beta=\frac{1}{2}$

所以将满足上述参数条件的一族公式（4）称为二阶龙格-库塔公式。当参数满足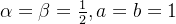 $\alpha=\beta=\frac{1}{2},a=b=1$ 时，二阶龙格-库塔法就是改进欧拉法。

2、三阶龙格-库塔公式

同二阶推导类似，三阶泰勒级数数值格式写成一般格式：

$\left\{\begin{matrix} y_{i+1}=y_{i}+\alpha k_{1}+\beta k_{2} +\gamma k_{3}\\ k_{1}=hf(x_{i},y_{i}) \\ k_{2}=hf(x_{i}+ah,y_{i}+bk_{1}) \\ k_{3}=hf(x_{i}+ch,y_{i}+dk_{1}+ek_{2}) \end{matrix}\right.$

对于上式，只要满足：

$\alpha+\beta+\gamma=1,a\beta+c\gamma=\frac{1}{2},c=d+e,a=b,a^{2}\beta+c^{2}\gamma=\frac{1}{3},ae\gamma=\frac{1}{6}$

所以将满足上述参数条件的一族公式称为三阶龙格-库塔公式，可以取一组简单的解，得到一组简单的三阶龙格-库塔公式。

$\alpha=\frac{1}{6},\beta=\frac{2}{3},\gamma=\frac{1}{6},a=b=\frac{1}{2},c=1,d=-1,e=2$

$\left\{\begin{matrix} y_{i+1}=y_{i}+ \frac{1}{6}(k_{1}+ 4k_{2} + k_{3})\\ k_{1}=hf(x_{i},y_{i}) \\ k_{2}=hf(x_{i}+\frac{1}{2}h,y_{i}+\frac{1}{2}k_{1}) \\ k_{3}=hf(x_{i}+h,y_{i}-k_{1}+2k_{2}) \end{matrix}\right.$

3、四阶龙格-库塔公式

数值计算中通常采用四阶龙格-库塔公式，推导过程与前述类似，四阶泰勒级数数值格式写成一般格式:

$\left\{\begin{matrix} y_{i+1}=y_{i}+\lambda_{1}k_{1}+\lambda_{2}k_{2}+\lambda_{3}k_{3}+\lambda_{4}k_{4}\\ k_{1}=hf(x_{i},y_{i}) \\ k_{2}=hf(x_{i}+\alpha_{1}h,y_{i}+\beta_{1}k_{1}) \\ k_{3}=hf(x_{i}+\alpha_{2}h,y_{i}+\gamma_{1}k_{1}+\gamma_{2}k_{2}) \\ k_{4}= hf(x_{i}+\alpha_{3}h,y_{i}+\mu_{1}k_{1}+\mu_{2}k_{2}+\mu_{3}k_{3}) \end{matrix}\right.$

对于上式，只要满足：

$\left\{\begin{matrix} \lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}=1\\ \alpha_{1}=\beta_{1} \\ \alpha_{2}=\gamma_{1}+\gamma_{2} \\ \alpha_{3}=\mu_{1}+\mu_{2}+\mu_{3} \\ \alpha_{1}\lambda_{2}+\alpha_{2}\lambda_{3}+\alpha_{3}\lambda_{4}=\frac{1}{2} \\ \alpha^{2}_{1}\lambda_{2}+\alpha^{2}_{2}\lambda_{3}+\alpha^{2}_{3}\lambda_{4}=\frac{1}{3} \\ \alpha^{3}_{1}\lambda_{2}+ \alpha^{3}_{2}\lambda_{3}+\alpha^{3}_{3}\lambda_{4}=\frac{1}{4}\\ \alpha_{1}\gamma_{2}\lambda_{3}+(\alpha_{1}\mu_{2}+\alpha_{2}\mu_{3})\lambda_{4}=\frac{1}{6}\\ \alpha_{1}\alpha_{2}\gamma_{2}\lambda_{3}+\alpha_{3}(\alpha_{1}\mu_{2}+\alpha_{2}\mu_{3})\lambda_{4} =\frac{1}{8}\\ \alpha^{2}_{1}\gamma_{2}\lambda_{3}+(\alpha^{2}_{1}\mu_{2}+\alpha^{2}_{2}\mu_{3})\lambda_{4}=\frac{1}{12} \\ \alpha_{1}\gamma_{2}\mu_{3}\lambda_{4}=\frac{1}{24} \end{matrix}\right.$

可以取下列满足条件的一组解，得到最常用的四阶龙格-库塔公式：

$\lambda_{1}=\lambda_{4}=\frac{1}{6},\lambda_{2}=\lambda_{3}=\frac{1}{3},\alpha_{1}=\alpha_{2}=\frac{1}{2},\alpha_{3}=1,\beta_{1}=\frac{1}{2},$

$\gamma_{1}=0,\gamma_{2}=\frac{1}{2},\mu_{1}=\mu_{2}=0,\mu_{3}=1$

$\left\{\begin{matrix} y_{i+1}=y_{i}+\frac{1}{6}(k_{1}+2k_{2}+2k_{3}+k_{4})\\ k_{1}=hf(x_{i},y_{i})\\ k_{2}=hf(x_{i}+\frac{1}{2}h,y_{i}+\frac{1}{2}k_{1}) \\ k_{3}=hf(x_{i}+\frac{1}{2}h,y_{i}+\frac{1}{2}k_{2}) \\ k_{4}=hf(x_{i}+h,y_{i}+k_{3}) \end{matrix}\right.$

三、算例实现

与欧拉法、梯形法、改进欧拉法一样，求相同的初值问题

$\left\{\begin{matrix} y^{'}=-\frac{0.9}{1+2x}y &, \space\space\space\space 0<x\leqslant 0.1 \\ y(0) = 1, & \end{matrix}\right.$

步长h=0.02。已知精确解为： $y(x)=(1+2x)^{-0.45}$

代码如下：

#include <stdlib.h>
#include <stdio.h>
#include <cmath>

int main(int argc, char* argv[])
{
        int i,N;
        double a,b,h,x0,x1,y0,y1,yexact,err;
        double k1,k2,k3,k4;
        double f(double x, double y);
        double exact(double x);

        a=0.0;
        b=0.1;
        N=5;
        h=(b-a)/N;

        i=1;
        x0=a;
        y0=1.0;

        do
        {
                x1=x0+h;
                k1=h*f(x0,y0);
                k2=h*f(x0+0.5*h,y0+0.5*k1);
                k3=h*f(x0+0.5*h,y0+0.5*k2);
                k4=h*f(x1,y0+k3);
                y1=y0+(k1+2*k2+2*k3+k4)/6.0;
                yexact=exact(x1);
                err=fabs(y1-yexact);
                printf("x=%.2f,   y=%f,   exact=%f,   err=%.10f.\n",x1,y1,yexact,err);
                i++;
                x0=x1;
                y0=y1;
        }while(i<=N);

        return 0;
}

double f(double x, double y)
{
        return -0.9*y/(1.0+2*x);
}

double exact(double x)
{
        return pow((1.0+2*x),-0.45);

N=5时，运行结果如下（并与欧拉法、梯形法、改进欧拉法对比）：

++++++++++++++++++++++四阶龙格-库塔法+++++++++++++++++++++++
x=0.0200,   y=0.982506,   exact=0.982506,   err=0.0000000003.
x=0.0400,   y=0.965960,   exact=0.965960,   err=0.0000000006.
x=0.0600,   y=0.950281,   exact=0.950281,   err=0.0000000008.
x=0.0800,   y=0.935393,   exact=0.935393,   err=0.0000000010.
x=0.1000,   y=0.921231,   exact=0.921231,   err=0.0000000011.

+++++++++++++++++++++++++预估-校正法++++++++++++++++++++++++++++
x[1]=0.0200,   y[1]=0.982324,   exact=0.982506,   err=0.000182.
x[2]=0.0400,   y[2]=0.965616,   exact=0.965960,   err=0.000344.
x[3]=0.0600,   y[3]=0.949791,   exact=0.950281,   err=0.000490.
x[4]=0.0800,   y[4]=0.934772,   exact=0.935393,   err=0.000621.
x[5]=0.1000,   y[5]=0.920492,   exact=0.921231,   err=0.000739.

+++++++++++++++++++++++++++梯形法++++++++++++++++++++++++++++++
x[1]=0.0200,   y[1]=0.982498,   exact=0.982506,   err=0.000008.
x[2]=0.0400,   y[2]=0.965946,   exact=0.965960,   err=0.000015.
x[3]=0.0600,   y[3]=0.950260,   exact=0.950281,   err=0.000021.
x[4]=0.0800,   y[4]=0.935367,   exact=0.935393,   err=0.000026.
x[5]=0.1000,   y[5]=0.921201,   exact=0.921231,   err=0.000030.

++++++++++++++++++++++++++++欧拉法+++++++++++++++++++++++++++++
x[1]=0.0200,   y[1]=0.982000,   exact=0.982506,   err=0.000506.
x[2]=0.0400,   y[2]=0.965004,   exact=0.965960,   err=0.000957.
x[3]=0.0600,   y[3]=0.948920,   exact=0.950281,   err=0.001360.
x[4]=0.0800,   y[4]=0.933670,   exact=0.935393,   err=0.001723.
x[5]=0.1000,   y[5]=0.919182,   exact=0.921231,   err=0.002049.

N=10时，运行结果如下（并与欧拉法、梯形法、改进欧拉法对比）：

++++++++++++++++++++++++四阶龙格-库塔法+++++++++++++++++++++++
x=0.0100,   y=0.991128,   exact=0.991128,   err=0.0000000000.
x=0.0200,   y=0.982506,   exact=0.982506,   err=0.0000000000.
x=0.0300,   y=0.974120,   exact=0.974120,   err=0.0000000000.
x=0.0400,   y=0.965960,   exact=0.965960,   err=0.0000000000.
x=0.0500,   y=0.958017,   exact=0.958017,   err=0.0000000000.
x=0.0600,   y=0.950281,   exact=0.950281,   err=0.0000000001.
x=0.0700,   y=0.942742,   exact=0.942742,   err=0.0000000001.
x=0.0800,   y=0.935393,   exact=0.935393,   err=0.0000000001.
x=0.0900,   y=0.928225,   exact=0.928225,   err=0.0000000001.
x=0.1000,   y=0.921231,   exact=0.921231,   err=0.0000000001.

+++++++++++++++++++++++++预估-校正法+++++++++++++++++++++++++++
x[1]=0.0100,   y[1]=0.991081,   exact=0.991128,   err=0.000047.
x[2]=0.0200,   y[2]=0.982413,   exact=0.982506,   err=0.000092.
x[3]=0.0300,   y[3]=0.973985,   exact=0.974120,   err=0.000135.
x[4]=0.0400,   y[4]=0.965786,   exact=0.965960,   err=0.000175.
x[5]=0.0500,   y[5]=0.957805,   exact=0.958017,   err=0.000213.
x[6]=0.0600,   y[6]=0.950032,   exact=0.950281,   err=0.000248.
x[7]=0.0700,   y[7]=0.942459,   exact=0.942742,   err=0.000283.
x[8]=0.0800,   y[8]=0.935078,   exact=0.935393,   err=0.000315.
x[9]=0.0900,   y[9]=0.927879,   exact=0.928225,   err=0.000346.
x[10]=0.1000,   y[10]=0.920856,   exact=0.921231,   err=0.000375.

++++++++++++++++++++++++++++梯形法+++++++++++++++++++++++++++++
x[1]=0.0100,   y[1]=0.991127,   exact=0.991128,   err=0.000001.
x[2]=0.0200,   y[2]=0.982504,   exact=0.982506,   err=0.000002.
x[3]=0.0300,   y[3]=0.974117,   exact=0.974120,   err=0.000003.
x[4]=0.0400,   y[4]=0.965957,   exact=0.965960,   err=0.000004.
x[5]=0.0500,   y[5]=0.958013,   exact=0.958017,   err=0.000004.
x[6]=0.0600,   y[6]=0.950276,   exact=0.950281,   err=0.000005.
x[7]=0.0700,   y[7]=0.942736,   exact=0.942742,   err=0.000006.
x[8]=0.0800,   y[8]=0.935386,   exact=0.935393,   err=0.000006.
x[9]=0.0900,   y[9]=0.928218,   exact=0.928225,   err=0.000007.
x[10]=0.1000,   y[10]=0.921223,   exact=0.921231,   err=0.000008.

++++++++++++++++++++++++++++欧拉法+++++++++++++++++++++++++++++
x[1]=0.0100,   y[1]=0.991000,   exact=0.991128,   err=0.000128.
x[2]=0.0200,   y[2]=0.982256,   exact=0.982506,   err=0.000250.
x[3]=0.0300,   y[3]=0.973756,   exact=0.974120,   err=0.000364.
x[4]=0.0400,   y[4]=0.965488,   exact=0.965960,   err=0.000473.
x[5]=0.0500,   y[5]=0.957442,   exact=0.958017,   err=0.000575.
x[6]=0.0600,   y[6]=0.949609,   exact=0.950281,   err=0.000672.
x[7]=0.0700,   y[7]=0.941978,   exact=0.942742,   err=0.000764.
x[8]=0.0800,   y[8]=0.934541,   exact=0.935393,   err=0.000851.
x[9]=0.0900,   y[9]=0.927290,   exact=0.928225,   err=0.000934.
x[10]=0.1000,   y[10]=0.920218,   exact=0.921231,   err=0.001013.

可见，相同计算条件下，四阶龙格-库塔法具有更高的计算精度，近乎与解析解相等。但采用四阶龙格-库塔法在每一步计算中都需要计算4次的值，相比其它三种方法，计算量最大。