【LeetCode】day2：977 - 有序数的平方, 209 - 长度最小的子数组, 59 - 螺旋矩阵

LeetCode 代码随想录跟练 Day2

977.有序数的平方
209.长度最小的子数组
59.螺旋矩阵

977.有序数的平方

题目描述：

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。
示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

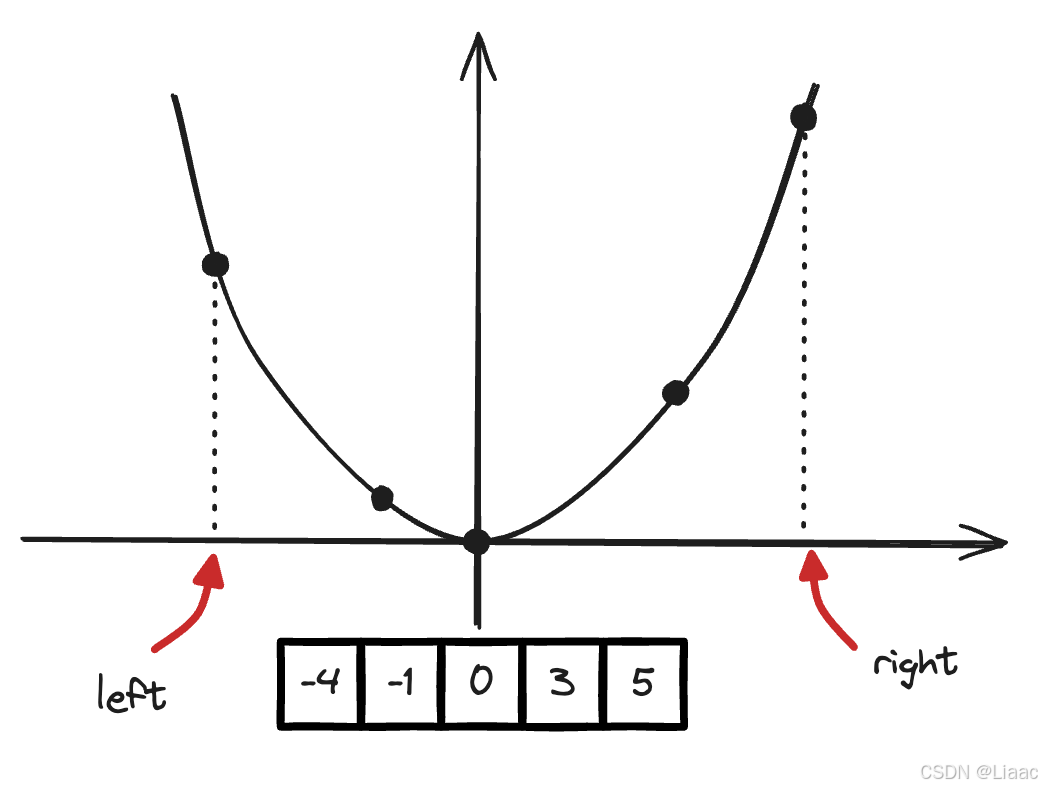
所给数组有序，则数组中每个数平方的排列一定是(非严格)递增(非负数)或先递减后递增，参考函数 $y = x^2$
在这里插入图片描述

取左右两指针从两侧分别出发遍历数组，比较对应元素平方值的大小，将大的那个存入新数组并移动指针，直到两指针相遇表示所有元素遍历完毕。代码如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;
        vector<int> res(nums.size(), 0);
        int cur = nums.size() - 1;// 指向新数组当前位置
        while (left <= right) {
            int left_square = nums[left] * nums[left];
            int right_square = nums[right] * nums[right];
            if (left_square < right_square) {
                res[cur--] = right_square;
                --right; 
            } else {
                res[cur--] = left_square;
                ++left;
            }
        }
        return res;
    }
};

209.长度最小的子数组

题目描述：

给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。
示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

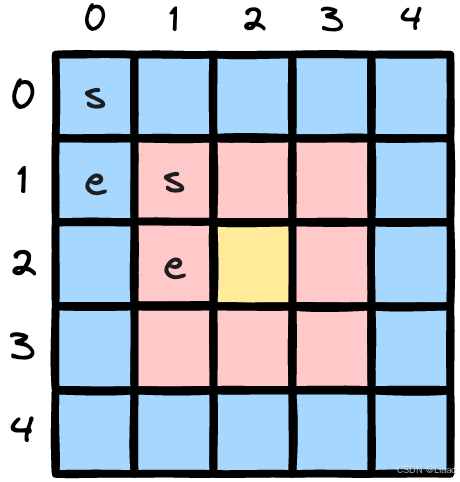
直观思路是取双指针left和right，left从左到右遍历数组，在每次遍历时right从left处出发求和直到总和大于target，将当前区间长度和res比较取最小值作为res。此处由于目的是取最小且长度不能设为初值0，所以初值设一个大于数组长度的值用来标识是否找到过满足条件的区间。代码如下：

lass Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int res = INT_MAX;
        for (int left = 0; left < nums.size(); ++left) {
            int sum = 0;
            for (int right = left; right < nums.size(); ++right) {
                sum += nums[right];
                if (sum >= target) {
                    int len = right - left + 1;
                    res = res > len ? len : res;
                    break;
                }
            }
        }
        return res == INT_MAX ? 0 : res;
    }
};

此时代码的时间复杂度为 $O(n^2)$ ，在用例数组长度过长时会超时，因此需要进行优化。注意到题目有个前提是数组中元素均为正整数，上述代码也是基于这一前提的，这一点保证了当right前进时总和一定是增大的，对于当前区间当区间长度减小时总和一定是减小的。
又由于题目结果所找的结果是子数组(连续区间)，结合以上两点，可令left和right同时移动，当sum小于target时移动right寻找符合条件的区间；当sum大于等于target后表示当前区间符合，此时right停止移动，left向前直到使总和回到小于target状态。重复这个过程直到right到达数组末端表示遍历完成。代码如下：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int res = INT_MAX;
        int left = 0;
        int sum = 0;
        for (int right = 0; right < nums.size(); ++right) {
            sum += nums[right];
            while (sum >= target) {
                int len = right - left + 1;
                res = res > len ? len : res;
                sum -= nums[left++];
            }
        }
        return res == INT_MAX ? 0 : res;
    }
};

59.螺旋矩阵

题目描述：

给你一个正整数 n ，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1：

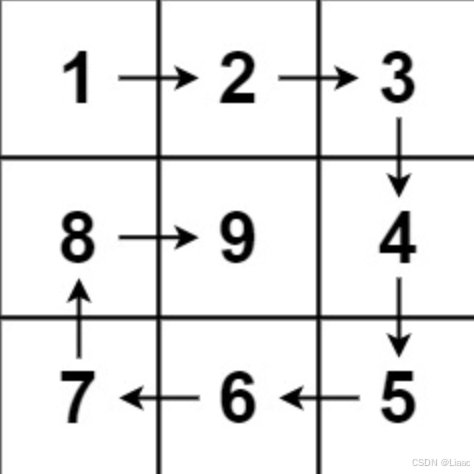
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：
输入：n = 1
输出：[[1]]

以顺时针螺旋的方式在长宽均为n的二维数组里画正方形，过程可以拆分如下
在这里插入图片描述
观察到每个正方形的横竖分别有两条边，按照这个方式在一个长为n的二维矩阵中能从外向内画出的正方形个数 $n /2$ ，且当n为奇数时画到最后一层会剩下单个方块，再额外对其进行填充，代码如下：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0));
        int round = n / 2;
        int len = n - 1;
        int num = 1;
        for (int cur = 0; cur < round; cur++) {
            int i = cur;
            int j = cur;
            // 向右
            while (j < len - cur) {
                res[i][j++] = num++;
            }
            // 向下
            while (i < len - cur) {
                res[i++][j] = num++;
            }
            // 向左
            while (j > cur) {
                res[i][j--] = num++;
            }
            // 向上
            while (i > cur) {
                res[i--][j] = num++;
            }
        }
        if (n % 2 == 1) {
            res[n / 2][n / 2] = num;
        }
        return res;
    }
};

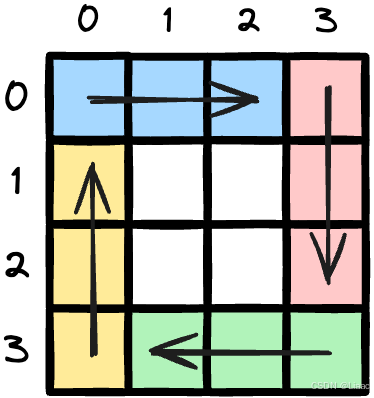
按照需要画出的正方形的圈数(n/2)进行循环，进入循环时当前的圈数(cur)对应的元素nums[cur][cur]就是当前正方形的左上角。用len表示二维数组的边界的索引，使用边界索引减去当前圈数(len - cur)表示当前轮次向右和向下的边界，当前圈数(cur)也表示当前轮次向左和向上的边界。每个循环的四个方向示例如下图：
在这里插入图片描述