目录
1.1 从感知机到神经网络
感知机:
① 感知机是具有输入和输出的算法,给定一个输入后,将输出一个既定的值
② 感知机将权重和偏置设定为参数
③ 单层感知机只能表示线性空间,但是多层感知机可以表示非线性空间
引入神经网络:
神经网络最左边一列称为输入层,最右边的一列成为输出层,中间的一列称为中间层(隐藏层)。输入层到输出层依次记作第0层、第1层、第2层。
1.1.1 由感知机引入
图中的感知机接收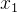

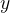
 | (1.2) |
其中:b表示的是偏置,用于控制神经元被激活的容易程度,

改写公式(1.2),得到(1.3)和(1.4)
 | (1.3) |
 | (1.4) |
(1.3)中,输入信号的总和会被函数h(x)转换,转换后的数值就是输出y,之后(1.4)表达的含义与(1.2)中表达的相同
1.1.2 引入激活函数(连接感知机与神经网络的桥梁)
函数
下面改写(1.3),分两个阶段进行,先计算输入信号的加权总和,然后用激活函数转换这一个总和,可以分成下面两个式子
 | (1.5) |
 | (1.6) |
(1.5)式计算加权输入信号和偏置的总和,记作

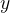
此处称
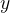
1.2 激活函数(连接感知机与神经网络的桥梁)
(1.4)表示的激活函数以阈值为界限,一旦输入超过阈值,就切换输出,这样的函数称为:阶跃函数
1.2.1 sigmoid函数
神经网络经常使用的一个激活函数是,(1.7)表示的sigmoid函数
 | (1.7) |
sigmoid仅仅是一个函数,函数就是给定某个输入后,会返回某个输出的转换器。使用该函数作为激活函数,进行信号的转换,转换后的信号被送到下一个神经元
1.2.2 作出阶跃函数和sigmoid函数
运行以下代码,做出相应的函数曲线
import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
y = x>0
#不等式生成的是bool(TRUE FALSE),使用astype转换为int型
return y.astype(np.int)
def sigmoid(x):
y = 1/ (1 + np.exp(-x))
return y
x = np.arange(-5.0,5.0,0.1)
y1 =step_function(x)
y2 = sigmoid(x)
plt.plot(x,y1,label='step_function')
plt.plot(x,y2,linestyle='--',label="sigmoid(x)")
plt.xlabel("x")
plt.ylabel("y")
plt.title('step_function&sigmoid(x)')
plt.legend()
plt.show()观察图,可以注意到的是平滑性的不同,sigmoid函数是一条平滑的曲线,输出随着输入发生连续性的变化。阶跃函数以0为界限,输出发生急剧性变化。sigmoid的平滑性对神经网络具有很重要的意义。
另有不同的是,阶跃函数只能返回0或1,但是sigmoid函数可以返回多个不同的实数。可以清晰的理解为感知机中神经元之间流动的是0或者1的二元信号,而神经网络中流动的是连续的实数数值信号。
有一比喻很恰当,阶跃函数就像敲石头一样,只做出是否传送信号(0或者1)两个动作。sigmoid就像火车,根据轨道相应的调整自己的行进方向。
两函数的相同点,虽然两个在平滑性上有差异,但是从宏观角度来讲,他们有相似的形状是,两者的结构都是:“输入小时,输出接近0(为0);随着输入增大,输出向1靠近(变成1)”.可以理解为,输入信号为重要信息的时候,阶跃函数和sigmoid函数都会输出比较大的数值,当输出信号为不重要的信息,两者均输出较小的数值。同时,不管输入信号有多么的小,或者有多大,输出信号的数值都在0到1之间。
1.2.3 非线性函数
上面的两个函数均为非线性函数,对于神经网络,激活函数必须使用非线性函数,因为使用线性函数,加深神经网络的层数就没有意义了。直观理解就是,假设将h(x)=c*x作为激活函数,将


1.2.4 ReLU函数
ReLU函数在输入大于0的时候,直接输出该值;在输入小于等于0的时候,输出0
可以表示为如下式
 | (1.8) |
可以通过以下代码来实现,
import numpy as np
def relu(x):
return np.maximum(0,x)函数图像如下
1.3 多维数组的运算
1.3.1 多维数组
多维数组就是数字的集合,数字排成一列的集合、排成长方体的集合、排成三维形状或者(更加一般化的)N维状的集合都称为多维数组。深度学习中一般使用numpy来生成多维数组。
数组的维数可以通过np.dim()函数来获得,数组的形状可以通过实例变量shape获得
1.3.2 神经网络的内积
使用NumPy矩阵来实现神经网络,如下图
实现该神经网络的时候,要注意X,W,Y的形状,特别是X和W对应维度的元素个数是否是一致的。
使用np.dot(x,w)可以计算两多维数组的点积。
1.4 3层神经网络的实现
以下图的3层神经网络为对象,实现从输入到输出的(前向)处理。代码通过NumPy来实现
3层神经网络:输入层(第0层)有2个神经元,第1个隐藏层(第1层)有3个神经元,第2个隐藏层(第2层)有2个神经元,输出层(第3层)有2个神经元
下面定义符号如下
也就是


1.4.1 各层间信号传递的实现
从输入层到第1层的信号传递:
使用式(1.9)表示如下
 | (1.9) |
也可以表示为:
| | (1.10) |
表示的意义如下:
用代码实现如下,使用的激活函数为sigmoid函数。
import numpy as np
X = np.array([1.0,0.5])
W1 = np.array([[0.1, 0.3, 0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X,W1) + B1
#使用sigmoid函数来实现
Z1 = sigmoid(A1)
print(A1)
print(Z1)从第1层到第2层的信号传递:
用代码实现如下,使用的激活函数为sigmoid函数。
W2 = np.array([[0.1, 0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
print(A2)
print(Z2)从第2层到输出层的信号传递:
用代码实现,这里使用的为identity_function()函数(也称为恒等函数),并且将其作为输出层的激活函数
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(Z2,W3) + B3
Y = identity_function(A3)输出层所使用的激活函数,要根据求解问题的性质来决定,一般回归问题可以使用恒等函数,二元分类问题可以使用sigmoid函数,多元分类问题可以使用softmax函数。
代码总体实现如下:
import numpy as np
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1, 0.4],[0.2, 0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1, 0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forward(network,x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y =identity_function(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)此处定义了init_network()和forward()函数, init_network()函数会进行权重和偏置的初始化,并且将他们保存在字典变量network中。forward()封装了将输入信号转换为输出信号的处理过程。
1.5 输出层的设计
神经网络可以用在分类问题和回归问题中,需要根据具体情况来改变输出层的激活函数:一般情况下,回归问题用恒等函数,分类问题用softmax函数。
分类问题是数据属于哪一个类别的问题,比如,区分图像中的人是男性还是女性;回归问题是根据某个输入预测一个(连续的)数值的问题。比如,根据一个人的图像就预测这个人体重的问题可以认为是回归问题。
1.5.1 恒等函数和softmax函数
恒等函数对于输入的信息,不加以任何改动直接输出。可以用下面的神经网络来表示
分类问题中使用的softmax函数可以用下面的公式来表示(1.11)
 | (1.11) |
式中:表示输出层共有n个神经元,计算第k个神经元的输出

使用python实现softmax函数如下:
函数的特点为:其输出总是为0.0-1.0的实数,并且,输出值的总和为1。这是该函数的一个重要性质,因为由于这个可以把softmax函数的输出解释为“概率”。也就是可以理解为可以用概率的(统计的)方法处理问题。
注意:即使使用该函数,输入值和输出值的元素间的大小关系并没有改变,并且神经网络只把输出值最大的神经元所对应的类别作为识别结果。即使使用softmax函数,输出值最大的神经元的位置也不会改变。故神经网络在进行分类的时候,输出层的softmax函数可以省略。
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y小总结:求解机器学习问题的步骤可以分为学习和推理两个阶段,首先,在学习阶段进行模型的学习,然后,在推理阶段,用学到的模型对未知的数据进行推理(分类)。
1.5.2 输出层的神经元数量
对于分类问题,输出层神经元的数量一般设置为类别的量,比如对于某个输入的图像,预测的是图中数字0-9中哪一个的问题,可以将输出层的神经元设置为10个。如下图所示:图中输出层的神经元的数值用不同的灰度来表示,例子中颜色最深的神经元输出的值最大,表明这个是神经元所预测的类别。
1.6 手写数字识别
这里假设的是学习已经全部结束,使用学习到的参数,先实现神经网络的“推理处理”,这个也被称为神经网路的前向传播。
使用神经网络解决问题的时候,需要首先使用训练数据(学习数据)进行权重参数的学习,进行推理的时候,使用刚才学习到的参数,对输入的数据进行分类。
1.6.1 MNIST数据集
该数据集的使用方法一般是,先用训练图像进行学习,再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。MNIST的图像数据都是28像素*28像素的灰度图像,各个像素之间的取值再0-255之间,每个图像数据都相应的标有“7”,“2”,“1”等标签。
读入MNIST的代码如下
import sys, os
sys.path.append(os.pardir)
from mnist import load_mnist
(x_train,t_train),(x_test,t_test) =
load_mnist(normalize=True,flatten=True)load_minist函数以(训练图像,训练标签),(测试图像,测试标签)的形式返回读入的MNIST数据。
load_mnist(normalize=True,flatten=True,one_hot_label=False)中
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from mnist import load_mnist
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
# 可修改参数:预测测试集中的哪一张图片
img = x_train[0]
label = t_train[0]
print("当前图片显示的数字是:{}".format(label)) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变为原来的尺寸
print(img.shape) # (28, 28)
img_show(img)显示出来的图像如下图所示
1.6.2 神经网络的推理处理
使用MNIST数据集实现神经网路的推理处理,神经网络的输入层有784个神经元,输出层有10个神经元。其中,输入层神经元个数来自图像的像素28*28=784,10来源于10类别分类。此外,该神经网络有2个隐藏层,第一个隐藏层有50个神经元,第2个隐藏层有100个神经元。50和100可以设置为任何数值。
具体实现的python代码如下
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 获取概率最高的元素的索引
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))其中:init_network()会读入保存再pickle文件sample_weight.pkl中学习到的权重参数。
首先获得MNIST数据集,生成网络。接着用for语句逐一取出保存在x中的图像数据,用predict函数进行分类。该函数以Numpy数组的形式输出各个标签对应的概率。例如输出[0.1, 0.2, 0.3, 0.4],该数组表示“0”的概率为0.1。然后取出这个概率列表中的最大值的索引(第几个元素的概率最高?),作为预测结果。
程序中,将load_mnist函数的参数normalize设置为了True,函数内部会进行转换,将图像的各个像素值除以255,使得数据的值在0.0-1.0之间,这种操作(将数据限定到某个范围内的处理)叫做正规化,此外,对神经网络的输入数据进行某种既定的转换叫做预处理。
注意:预处理在神经网络中很实用,比如,利用数据整体的均值和标准差,移动数据,使得数据整体以0为中心分布,或者进行正规化,把数据的延伸控制在一定范围内。
1.6.3 批处理
对于只处理一张图像数据时,流程如下:
如果函数一次性打包处理100张图像,则流程如下:
输出Y表明,输入的100张图像的结果被一次输出了,这种打包方式为批。主要作用是在数据传送成为瓶颈的时候,减轻数据总线的负荷。
具体实现的代码如下
x,t = get_data()
network = init_network()
"批处理"
batch_size = 100 #批数量
accuracy_cnt = 0
#格式:range(start,end,step)
for i in range(0,len(x),batch_size):
#从输入数据中抽出批数据
#从i到i+batch_size之间的数据【0-100,100-200.】?切片处理?
x_batch = x[i:i+batch_size]
y_batch = predict(network,x_batch)
#设定参数axis=1,表示在该数组中,沿着行方向找到数值最大的元素索引
p = np.argmax(y_batch,axis=1)
#计算批次中预测正确的数量(True的个数),并累加在变量中
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print(y_batch.shape)
print("Accuracy:"+ str(float(accuracy_cnt)/len(x)))