数据结构--Map和Set

一.二叉搜索树

1.1 概念

二叉搜索树，又称二叉排序树，其是一棵空树或者具有以下性质的二叉树：

如果树的左子树不为空，则左子树上的所有结点的值都小于根节点的值
如果树的右子树不为空，则右子树上的所有结点的值都大于根节点的值
树的左右子树都分别为一棵二叉搜索树

1.2 二叉搜索树的简单实现

public class BinarySearchTree {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public TreeNode root;

    public boolean search(int val) { //查找值为val的结点
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val < val) { //当前结点的值小于val
                cur = cur.right; //在其右子树查找
            } else if (cur.val > val) { //当前结点的值大于val
                cur = cur.left; //在其左子树寻找
            } else { //当前结点的值等于val,查找成功
                return true;
            }
        }
        return false;
    }

    public void insert(int val) { // 插入值为val的结点
        // 1.按照二叉搜索树的性质,查找到要插入的结点
        // 2.插入新结点
        if (root == null) {
            root = new TreeNode(val);
            return;
        }
        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return;
            }
        }
        TreeNode newNode = new TreeNode(val);
        if (parent.val > val) {
            parent.left = newNode;
        } else {
            parent.right = newNode;
        }
    }

    public void remove(int val) { //删除值为val的结点
        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                // parent:待删除节点的父结点
                // cur:待删除结点
                removeNode(parent, cur);
            }
        }
    }

    private void removeNode(TreeNode parent, TreeNode cur) {
        if (cur.left == null) { //cur.left为空的情况
            if (cur == root) { //cur是root
                root = cur.right;
            } else if (cur == parent.left) { //cur不是root,cur是parent的左子结点
                parent.left = cur.right;
            } else { //cur不是root,cur是parent的右子结点
                parent.right = cur.right;
            }
        } else if (cur.right == null) { //cur.right为空的情况(与cur.left为空的情况相同)
            if (cur == root) {
                root = cur.left;
            } else if (cur == parent.left) {
                parent.left = cur.left;
            } else {
                parent.right = cur.left;
            }
        } else { //cur.left与cur.right都不为空的情况
            //使用替换法删除,在cur结点的右子树中寻找值最小的结点来替换cur的值
            TreeNode t = cur.right; //值最小的结点
            TreeNode tp = cur; //值最小结点的父结点
            while (t.left != null) {
                tp = t;
                t = t.left;
            }
            cur.val = t.val;
            if (tp.left == t) { //删除结点t
                tp.left = t.right;
            } else {
                tp.right = t.right;
            }
        }
    }
}

二.Map

2.1 概念

Map和Set是一种专门用来进行搜索的数据结构，一般把搜索的数据称为关键字(Key)，与关键字对应的称为值(Value)。Map是一个接口类，使用了Key-Value模型，类中存储的是<Key,Value>键值对，并且Key是唯一的，不能重复。Map内部使用了Map.Entry<K,V>的内部类来存放<Key,Value>键值对的映射关系

2.2 Map常用方法

方法	解释
V get(Object key)	返回key对应的value
V getOrDefault(Object key,V defaultValue)	返回key对应的value，key不存在，则返回`defaultValue`(默认值)
V put(K key,V value)	设置key对应的value
V remove(Object key)	删除key对应的映射关系
Set<K> keySet()	返回所有key的不重复集合
Collection<V> values()	返回所有value的可重复集合
Set<Map.Entry<K,V>> entrySet()	返回所有的`key-value映射关系`
boolean containsKey(Object key)	判断是否包含key
boolean containsValue(Object value)	判断是否包含value

2.3 Map使用注意点

Map是一个接口，不能直接实例化对象，如果要实例化对象，只能实例化其实现类TreeMap或者HashMap
Map中存放键值对的key是唯一的，value是可以重复的
在TreeMap中插入键值对时，key不能为空，否则会抛出NullPointerException(空指针)异常，value可以为空；HashMap的key和value都可以为空
Map中的key可以全部分离出来，存储到Set中进行访问
Map中的value也可以全部分离出来，存储到Collection的任意一个子集合中
Map中键值对的key不能直接修改，value可以修改，如果要修改key，只能将key删除掉再重新插入

2.4 TreeMap和HashMap的区别

Map	TreeMap	HashMap
底层结构	红黑树	哈希桶
插入/删除/查找时间复杂度	`O(log2N)`	`O(1)`
是否有序	关于key有序	无序
线程安全	不安全	不安全
插入/删除/查找区别	需要进行元素比较	通过哈希函数计算哈希地址
比较与覆写	key必须能够比较，否则会抛异常	自定义类型需要覆写equals和hashCode方法
应用场景	需要key有序场景下	不关心key是否有序，有更高的时间性能需求

2.5 HashMap底层知识点

HashMap的最大容量为2³⁰
当指定HashMap初始容量capacity时，生成的HashMap的容量为最接近capacity的二次幂的值(例如指定容量为20，实际容量为32；指定容量为1000，实际容量为1024)
未指定HashMap初始容量时，生成的HashMap默认容量为16
HashMap扩容时为2倍扩容
HashMap的put方法使用的是尾插法
如果HashMap中存储数组长度>=64，且各个桶中的单链表的长度>=8，HashMap就会树化(单链表转变成红黑树)

三.Set

3.1 概念

Set也是一个接口类，与Map不同，Set使用的是纯Key模型，类中只存储Key

3.2 Set常用方法

方法	解释
boolean add(E e)	添加元素，但是`重复元素不会添加`
void clear()	清空集合
boolean contains(Object o)	判断o是否在集合中
Iterator<E> iterator()	返回迭代器
boolean remove(Object o)	删除集合中的o
int size()	返回set中元素的个数
boolean isEmpty()	检测set是否为空，空返回true，否则返回false
Object toArray()	将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)	集合c中的元素是否在set中全部存在
boolean addAll(Collection<? extends E> c)	将集合c中的元素添加到set中，可达到去重的效果

3.3 Set使用注意点

Set是继承自Collection的一个接口类
Set中只存储了key，并且要求key唯一
实现Set接口的常用类有TreeSet和HashSet，还有LinkedHashSet(在HashSet的基础上维护了一个双向链表来记录元素的插入次序)
TreeSet底层使用Map实现，使用key与Object默认对象作为键值对插入到Map中
与Map类似，Set中的key也不能直接修改，如果修改key，要删除并重新插入
TreeSet不能插入null的key，HashSet可以

3.4 TreeSet与HashSet的区别

Set	TreeSet	HashSet
底层结构	红黑树	哈希桶
插入/删除/查找时间复杂度	O(log2N)	O(1)
是否有序	关于key有序	不一定有序
线程安全	不安全	不安全
插入/删除/查找区别	按照红黑树的特性来进行插入删除	计算key哈希地址再进行插入和删除
比较与覆写	key必须能够比较，否则会抛出异常	自定义类型需要覆写equals和hashCode方法
应用场景	需要key有序场景下	不关心key是否有序，有更高的时间性能需求

四.哈希表

4.1 概念

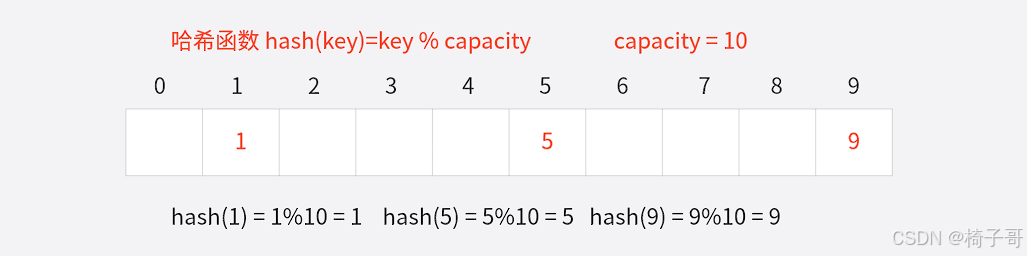
哈希表，又称散列表，是一种数据结构，其通过哈希函数(散列函数)在元素的存储位置与关键码之间建立一一映射的关系，从而实现快速的插入、搜索和删除操作

例如数据集合{1,5,9}，哈希函数设置为hash(key)=key%capacity；capacity为存储元素底层空间总大小

4.2 哈希冲突与避免

哈希冲突：对于两个不同的关键字，如果通过哈希函数计算出了相同的哈希地址，这种现象称为哈希冲突

由于哈希表底层数组容量往往小于实际存储的关键字数量，这就导致冲突的发生是必然的，但是我们可以通过一些方法尽量降低冲突率。冲突避免的方法有：

哈希函数设计：引起哈希冲突的原理可能是哈希函数的设计不够合理，常用哈希函数有直接定制法，除留余数法，平方取中法，折叠法，随机数法，数学分析法等
负载因子调节：负载因子α=填入表中的元素个数/哈希表的长度，α越大表明填入表中的元素越多，产生冲突的可能性就越大，反之则α越小，则填入表中元素越少，产生冲突的可能性越小。想要降低冲突率，就要降低负载因子，由于哈希表中元素个数是不可变的，我们可以通过调整哈希表中数组的大小来实现哈希冲突避免

4.3 冲突解决

解决哈希冲突的两种常见方法分别为闭散列和开散列

4.3.1 闭散列

闭散列，也称开放定址法，当发生哈希冲突时，如果哈希表没有被装满，说明在哈希表中还有空位置，这时可以把key存放到冲突位置中的下一个空位置去，下个空位置的具体寻找方法如下：
9. 线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止
10. 二次探测：线性探测会导致产生冲突的数据堆积在一起，二次探测为了避免这个问题，调整寻找下一个空位置的方法为(hash(key)+i^2^)%capacity (其中i=1,2,3,…)

4.3.2 开散列(哈希桶)

开散列，又称链地址法，对关键码集合用哈希函数计算哈希地址，具有相同地址的关键码归属于同一个子集合，每一个子集合称为一个桶，各个桶中的元素通过一条单链表(长度突破大于一定阈值后，转变为红黑树)连接起来，每条链表的头结点存储在哈希表中。在Java中，就使用了哈希桶这种方式来解决冲突

4.3.3 哈希桶的简单实现

public class HashBucket<K, V> {
    static class Node<K, V> {
        K key;
        V val;
        Node<K, V> next;

        public Node(K key, V val) {
            this.key = key;
            this.val = val;
        }
    }

    public Node<K, V>[] array = (Node<K, V>[]) new Node[10];
    public int usedSize;
    public static final double LOAD_FACTOR = 0.75; //负载因子

    public void put(K key, V val) {
        Node<K, V> node = new Node<>(key, val);
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K, V> cur = array[index];
        while (cur != null) {
            if (cur.key.equals(key)) {
                cur.val = val;
                return;
            }
            cur = cur.next;
        }
        node.next = array[index];
        array[index] = node;
        usedSize++;
        if (doLoadFactor() > LOAD_FACTOR) {
            reSize();
        }
    }

    public void reSize() {
        Node<K, V>[] newArray = new Node[array.length * 2];
        for (int i = 0; i < array.length; i++) {
            Node cur = array[i];
            while (cur != null) {
                int hash = cur.key.hashCode();
                int index = hash % newArray.length;
                Node curNext = cur.next;
                cur.next = newArray[index];
                newArray[index] = cur;
                cur = curNext;
            }
        }
        array = newArray;
    }

    public double doLoadFactor() {
        return usedSize * 1.0 / array.length;
    }

    public V get(K key) {
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K, V> cur = array[index];
        while (cur != null) {
            if (cur.key.equals(key)) {
                return cur.val;
            }
            cur = cur.next;
        }
        return null;
    }
}