一.小卷积核

一般指的都是大小为3*3的卷积核，可以有多个通道数
eg：一个3×3×64的卷积核就是指长×宽为3×3，64个过滤器（厚度为64）

1.一个5×5的卷积核可以用两个3×3的代替

例如：输入的特征图为64×64的，
① 用5×5的卷积核进行卷积，步长设为1，输出的特征图为ceil（（64-5+1）÷1）=60，即为60×60的大小
②用两个3×3的分别进行卷积，步长也设为1，
第一步：ceil（(64-3+1）÷1)=62
第二步：ceil（(62-3+1）÷1)=60
结果也为60*60
由上可见，两种结果是相同的，说明一个5×5的卷积核完全可以用两个3×3的代替

相似的，一个7×7的卷积核可以用三个3×3的代替；一个9×9的卷积核可以用四个3×3的代替…
大家若有不会进行卷积运算的，可以查看此文章
卷积运算

二.小卷积核优点

1.参数量少

就拿上边的那个例子说，两个3×3的卷积核参数量为3×3×2=18，一个5×5的卷积核参数量为5×5=25，可见小卷积核参数量要小（此处都是用1通道，若加入多通道，参数量更是成倍的增加，小卷积核参数量少的优势就更加的明显）

2.小卷积核堆叠使用，可以使得模型的非线性表达能力更好。

为什么这么说呢，是不是很摸不到头脑，卷积操作不都是线性的吗，不就是wx+b，从哪来的非线性呢，什么鬼。。。

其实我们神经网络里边，每一层卷积后都要跟一个激活层（要注意，写神经网络时，激活层可不能少），卷积层多了，激活层不也就多了，非线性表达能力不就更好啦！！

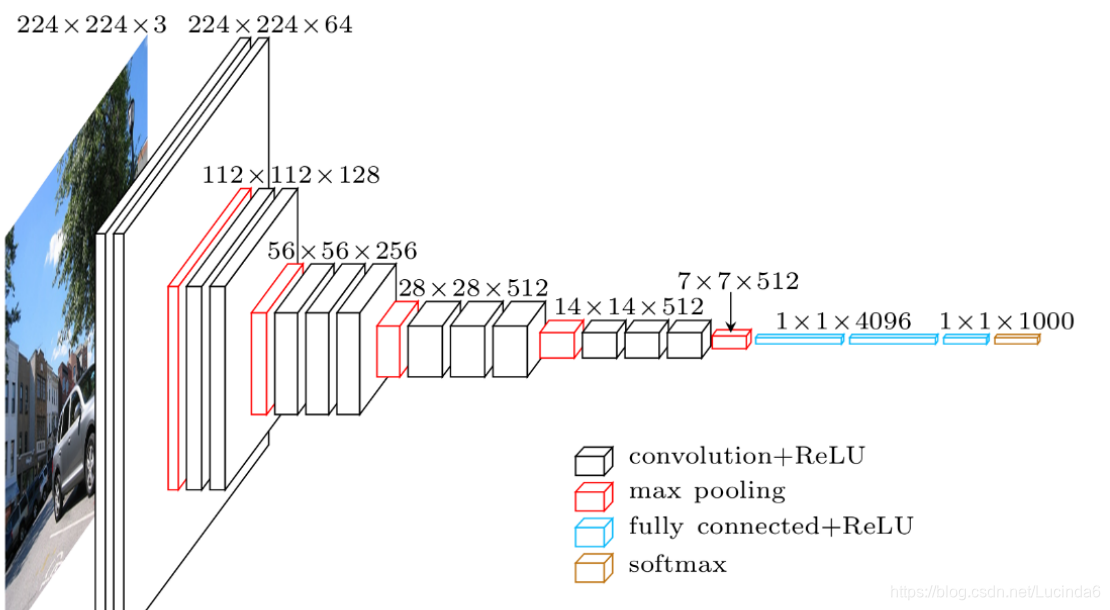
看这里VGG16

明确的标出了，卷积层和全连接层后边都要加一个激活函数

3.小卷积核堆叠使用，还能使模型的计算量减少

此处的计算量一般都是指乘法运算，加法就不算在内了
在这要为大家提供一个计算量计算的公式
计算量=(卷积核大小c×w×h)×(输出特征图大小c×w×h)
很容易想到，每做一次卷积进行的乘法操作，就是卷积核每个位置和对应位置相乘，那一次卷积操作的乘法运算量不就是卷积核的大小么，最后变成的不就是输出特征图的一个值吗；那要做多少次卷积，不就是特征图有多大，就做多少次么，所以能得到这个结果。

还拿上边的那个例子来说吧，
①一个5×5卷积的运算量为(5×5×1)×(60×60×1)=90000
②两个3×3卷积的运算量为(3×3×1)×(62×62×1)+(3×3×1)×(60×60×1)=34596+32400=66996
可以看出小卷积核的运算量是较少的

4.小卷积核堆叠使用可以达到和大卷积核一样的探测面积，还更能提取到有用特征，不会丢失重要特征。

从文章刚开始的部分就可得出，多个小卷积核完全可以替代一个大卷积核，而且输出特征图大小还可保持不变，多次卷积又代表着多次提取特征，还能更好的提取有用特征。

大家有什么不懂的地方，可以给我留言，谢谢观看