$⟶$ 论文链接

1.基于拉普拉斯算子的边缘检测 Laplacian based Edge Detection

你可能对这个算子非常熟悉：
$${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\text{\hspace{1em}(0)}$$
这个就是拉普拉斯算子（Laplacian），通过检测二阶导数的零交叉点来进行边缘检测。
不过，拉普拉斯算子对噪声（noise）非常敏感（highly sensitive），需要先进行低通滤波（low-pass filter），最常用的是高斯低通滤波器，表达式如下：
$$G_{\sigma }(x)=\frac{1}{2\pi {\sigma }^2}\exp (-\frac{||x|{|}^2}{2{\sigma }^2})\text{\hspace{1em}(1)}$$
其中：

• $\sigma$：高斯分布的标准差（standard deviation of Gaussian distribution），即高斯模板的尺度
• $x$：一个二维的坐标（a two-dimension co-ordinate）

最后，就是现在有名的拉普拉斯高斯算子（Laplacian of Gaussian, LoG）：
$${\nabla }^2(G_{\sigma }\ast I)=({\nabla }^2{G}_{\sigma })\ast I\text{\hspace{1em}(2)}$$
通过对高斯模板作二阶微分之后再对图像进行滤波可以降低计算量，提高效率，其中 $\ast$ 表示一个卷积操作。

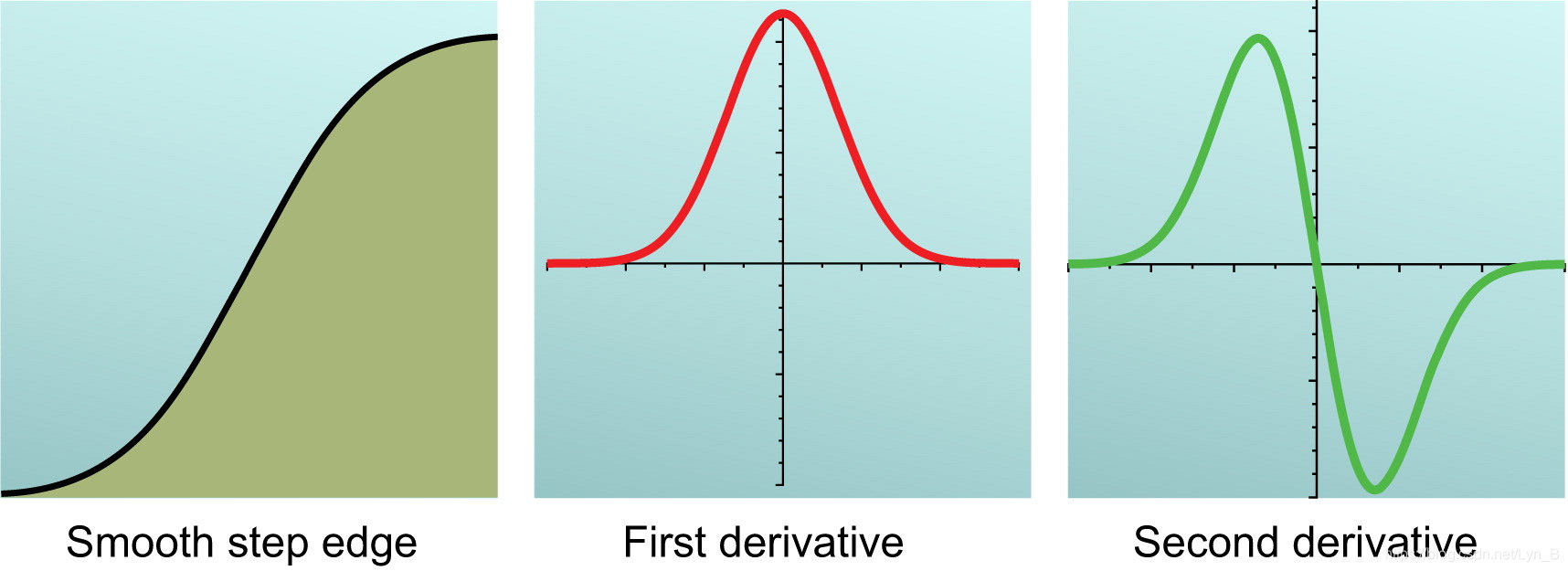
图 1-1 从左到右为：边缘，一阶导，二阶导

虽然这个算子是一个线性算子，但是我们在对图像进行滤波的时候（离散的），通常采用一个离散的模板去近似它，例如一个 $5\times 5$ 的核：
$$\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 0& 1& 2& 1& 0\\ 1& 2& -16& 2& 1\\ 0& 1& 2& 1& 0\\ 0& 0& 1& 0& 0\end{array}\right]\text{\hspace{1em}(3)}$$

2.高斯差分算子 Difference of Gaussian

拉普拉斯高斯算子（LoG）缺点：计算效率较低，因为计算缺乏可分性（not separable）。因此提出了另外一种方法：通过两个高斯模板的差分来近似这个拉普拉斯高斯算子，而显然这两个高斯模板是可分的：
通过对尺度（$\sigma$）进行一个微小的改变，来实现这个近似：
$$\underset{k\to 1}{\lim }\frac{G_{k\sigma }(x)-G_{\sigma }(x)}{k\sigma -\sigma }=\frac{\partial G}{\partial \sigma }=\sigma {\nabla }^{2}G\text{\hspace{1em}(4)}$$
最终，高斯差分算子如下：
$$D_{\sigma ,k}(x)=G_{\sigma }(x)-G_{k\sigma }(x)\approx -(1-k){\sigma }^2{\nabla }^2{G}_{\sigma }\text{\hspace{1em}(5)}$$
用来近似一个尺度归一化（scale-normalized）的负拉普拉斯高斯算子（negated Laplacian），其中：

• k：一个大于零的常数，通常设为 $1.6-byMarrandHildreth$
• $\sigma$：尺度，尺度归一化使得这个滤波的响应不会受到尺度变化的影响

从下图（b）可以看到，事实上高斯差分滤波是一个带通滤波（band-width filter），即，以这两个高斯低通滤波的截止频率为边界的带通滤波器：

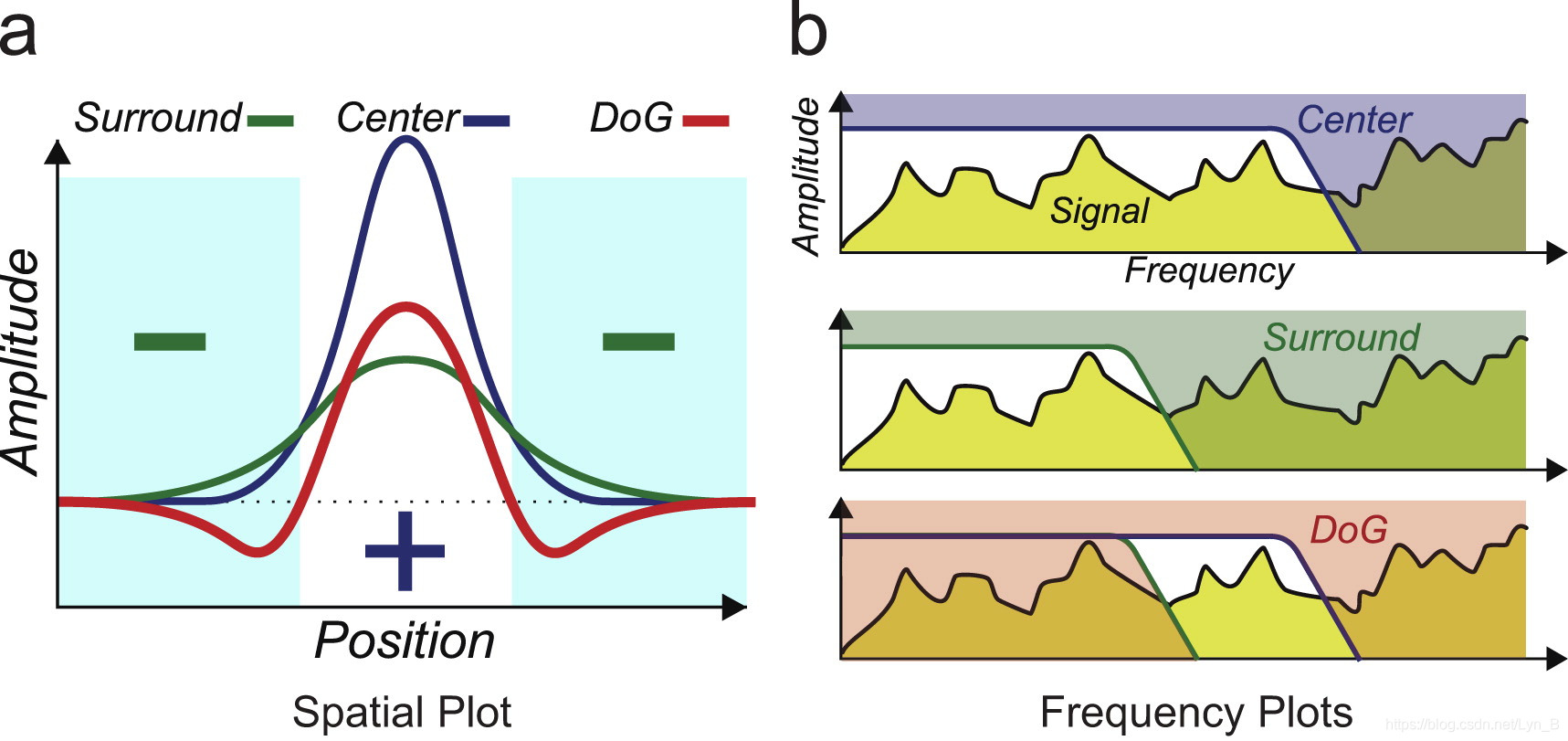
图2-1 空域表示和频域表示

代码：

# parameterization
# sigma for gaussian filter
sigma = 0.5
# proposed by Marr and Hildreth
k = 1.6
# threshold if thresholded DoG is expected
# epsilon = 0.1

# convert(mode) function's param - mode's options:
		# 1 ------------------（1位像素，黑白，每字节一个像素存储）
		# L ------------------（8位像素，黑白）
		# P ------------------（8位像素，使用调色板映射到任何其他模式）
		# RGB------------------（3x8位像素，真彩色）
		# RGBA------------------（4x8位像素，带透明度掩模的真彩色）
		# CMYK--------------------（4x8位像素，分色）
		# YCbCr--------------------（3x8位像素，彩色视频格式）
		# I-----------------------（32位有符号整数像素）
		# F------------------------（32位浮点像素）
img = Image.open(file).convert('L')
# gaussian filter with sigma
blur = filter.gaussian_filter(img, sigma)
# gaussian filter with sigma * k
blur_k = filter.gaussian_filter(img, sigma * k)
# get differenced image
differenced = blur - blur_k

# if using thresholding
#
# (width, height) = shape(img)
# for i in range(width):
# 	for j in range(height):
# 		if differenced[i,j] > epsilon:
# 			differenced[i,j] = 255
# 		else:
# 			differenced[i,j] = 0

3.扩展高斯差分算子 Extended Difference of Gaussian [1]

图 3-1 边缘提取算子结果对比 [1]

可以看到，第二行的边缘检测算子得到的图像效果和第一行有明显的差别：图像。阈值（threshold）的使用导致了这样的效果差异。
$$T_{ϵ}(u)=\{\begin{array}{l}\begin{array}{rlr}& 1,& u\ge ϵ\\ & 0,& otherwise\end{array}\end{array}\text{\hspace{1em}(6)}$$
这是一个简单的二分阈值函数。其中，$u$ 是在高斯差分图像中对应的二维坐标下的值，$ϵ$ 是设置的阈值。
此外，通过引入一个新的常数来调整高斯差分滤波的截止效果的强度（strength of inhibitory effect）：
$$D_{\sigma ,k,\gamma }(x)=G_{\sigma }(x)-\gamma \cdot G_{k,\sigma }(x)\text{\hspace{1em}(7)}$$
通过调整这个 $\gamma$ 值可以得到更多的风格效果变化。当这个值为 $1$ 时，则此时为一个普通的高斯差分，通常这个值的微小变化就可以对效果产生明显的影响：

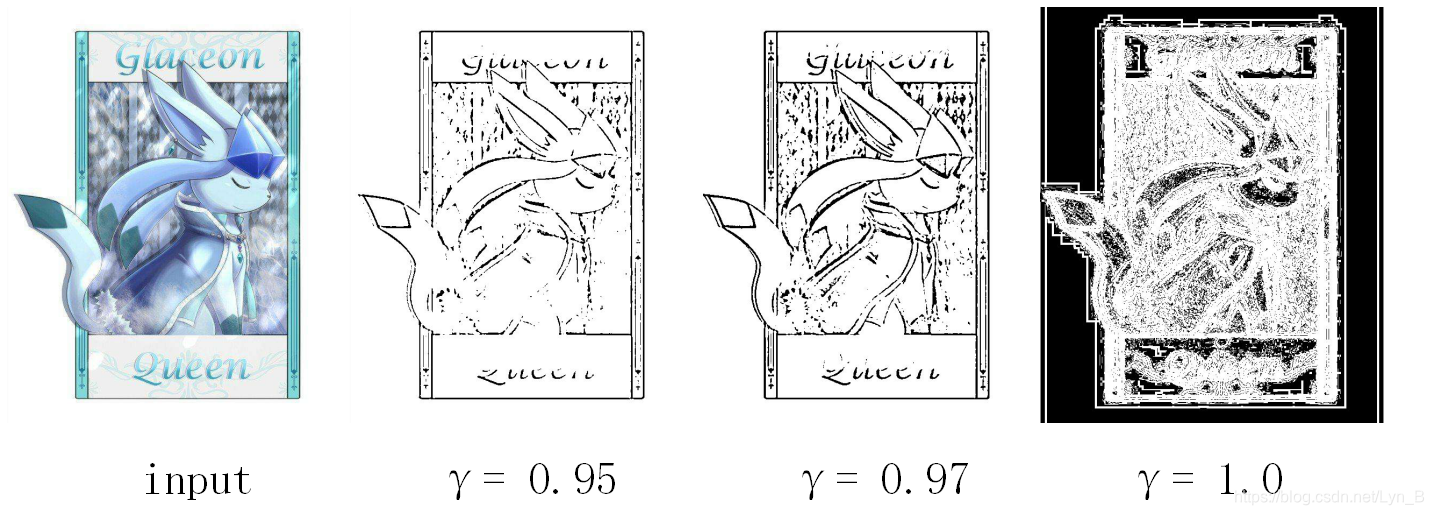
图 3-2 参数调整结果

如上图，我们可以明显的看到，当 $\gamma =1.0$ 变化到 $\gamma =0.97$ 时，效果发生了非常明显的变化，显然得到了更好的效果。
另外，再把前面的阈值二分函数换成一个连续的斜坡函数：
$$T_{ϵ}(u)=\{\begin{array}{l}\begin{array}{rlr}& 1,& u\ge ϵ\\ & 1+tanh(\phi \cdot (u-ϵ)),& otherwise\end{array}\end{array}\text{\hspace{1em}(8)}$$
这就是扩展高斯差分（eXtended Difference of Gaussian）。
通过对前面的式子进行变换，可以得到：
$$D_{\sigma ,k,\gamma }(x)=G_{\sigma }(x)-\gamma \cdot G_{k,\sigma }(x)=(1-\gamma )\cdot G_{\sigma }(x)+\gamma \cdot D_{\sigma ,k}(x)\text{\hspace{1em}(9)}$$
即，事实上，扩展高斯差分的结果是高斯模糊的结果和高斯差分结果的加权平均。
效果：

图 3-3 XDoG 结果

其中，$\mathbf{k}=1.6,\gamma =0.97,ϵ=0.1,\phi =10$
代码：

# parameterization
p = 1
phi = 10
epsilon = 150
k = 1.6
sigma = 0.5
# open images
img = Image.open(file).convert('L')
# gaussian filtering
blur = filters.gaussian_filter(img, sigma)
blur_k = filters.gaussian_filter(img, sigma* k)
# get differenced image
differenced = (p + 1) * blur - p * blur_k
# get shape
(x, y) = shape(img)
# thresholding
for i in range(x):
	for j in range(y):
		if differenced[i, j] >= epsilon:
			differenced[i, j] = 255
		else:
			differenced[i, j] = 255 + 255 * tanh(phi * (differenced[i, j] - epsilon))

3.1参数化调整 Re-parameterization of the XDoG

要求（desire）：

• 移除上文中参数互相之间的紧密依赖
• 更加符合我们直觉的（intuitive）参数（在调参上）
• 新的参数空间和旧的参数空间之间可以互相转化

通过对 $(9)$ 式除以 $\gamma -1$，就可以得到满足以上要求的参数化：
$$S_{\sigma ,k,p}(x)=\frac{D_{\sigma ,k,p}(x)}{\gamma -1}=G_{\sigma }(x)+p\cdot D_{\sigma ,k}(x)=(1+p)\cdot G_{\sigma }(x)-p\cdot G_{k\sigma }(x)\text{\hspace{1em}(10)}$$
最终得到：一个用图像锐化算子表示的扩展高斯差分。通过用 $p$ 取代原来的 $\gamma$，使得我们可以通过这个变量控制边缘的锐化效果而不会对模板产生影响。这样，$\gamma$ 就变成与像素值相关的阈值，我们可以更加直观的设置相应的参数值。
效果：

其中，$\mathbf{k}=1.6,\mathbf{p}=0.5,\sigma =0.1,\gamma =0.97,ϵ=0.1,\phi =10$

4.基于流的高斯差分 Flow-based Difference of Gaussian

将高斯差分算子（DoG）扩展成为基于流的高斯差分，把 $\sigma$ 用三个独立的参数代替：

• ${\sigma }_c$：控制用于对图像结构张亮进行高斯模糊的宽度
• ${\sigma }_e$：控制沿梯度方向的高斯差分滤波器的宽度。这个值越大，可以得到更多理想的细节，以及更宽的边缘线条
• ${\sigma }_m$：控制基于边缘正切值的线积分卷积的宽度

参考文献

[1] XDoG: An eXtended difference-of-Gaussians compendium including advanced image stylization,
Holger Winnemöllera, Jan EricKyprianidisb, Sven C.Olsen, Computers & Graphics Volume 36, Issue 6, October 2012, Pages 740-753