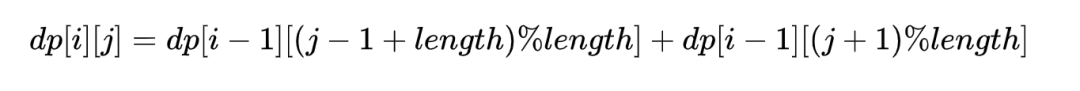◉ 一、数组
912. 排序数组
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104
题解
func Swap(x *int, y *int){
temp := *x
*x = *y
*y = temp
}
func Partition(nums *[]int, i int,j int) int{
idx := rand.Int()%(j-i+1)+i
Swap(&(*nums)[i],&(*nums)[idx])
x := (*nums)[i]
for i<j{
for i<j && (*nums)[j] >= x{
j--
}
(*nums)[i] = (*nums)[j]
for i<j && (*nums)[i]<=x {
i++
}
(*nums)[j] = (*nums)[i]
}
(*nums)[i] = x
return i
}
func quickSort(nums *[]int, s int, e int){
var m int
if (s<e){
m = Partition(nums,s,e)
quickSort(nums,s,m-1)
quickSort(nums,m+1,e)
}
}
func sortArray(nums []int) []int {
if len(nums) <=1 {
return nums
}
rand.New(rand.NewSource(time.Now().UnixNano()))
i,j := 0,len(nums)-1
quickSort(&nums,i,j)
return nums
}
1184. 公交站间的距离
难度:简单
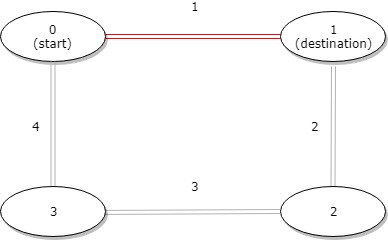
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
输入:distance = [1,2,3,4], start = 0, destination = 1
输出:1
解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
示例 2:
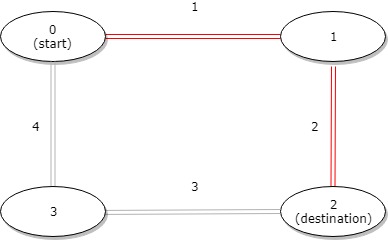
输入:distance = [1,2,3,4], start = 0, destination = 2
输出:3
解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
示例 3:
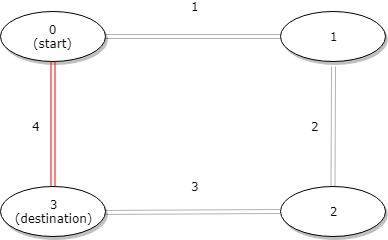
输入:distance = [1,2,3,4], start = 0, destination = 3
输出:4
解释:公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
题解
计算start-end的加和,计算这个范围外的加和,输出较小者。
class Solution {
public:
int distanceBetweenBusStops(vector<int>& nums, int start, int end) {
int d1 = 0, d2 = 0;
int l = min(start,end);
int r = max(start,end);
for(int i=0;i<nums.size();i++){
if(i>=l && i<r){d1 += nums[i];}
else{d2 += nums[i];}
}
return d1<d2?d1:d2;
}
};
1539. 第 k 个缺失的正整数
难度:简单
给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
请你找到这个数组里第 k 个缺失的正整数。
示例 1:
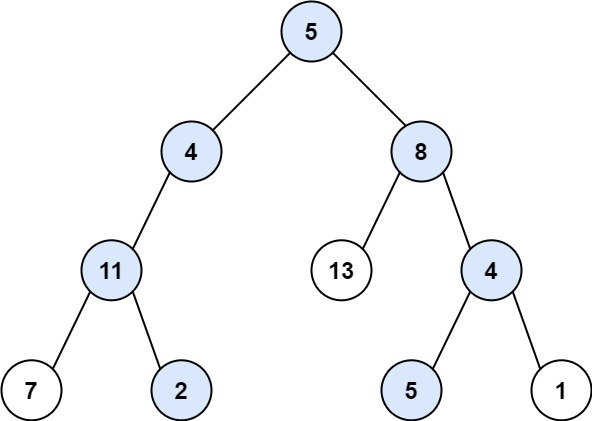
输入:arr = [2,3,4,7,11], k = 5
输出:9
解释:缺失的正整数包括 [1,5,6,8,9,10,12,13,...] 。第 5 个缺失的正整数为 9 。
示例 2:
输入:arr = [1,2,3,4], k = 2
输出:6
解释:缺失的正整数包括 [5,6,7,...] 。第 2 个缺失的正整数为 6 。
提示:
1 <= arr.length <= 10001 <= arr[i] <= 10001 <= k <= 1000- 对于所有
1 <= i < j <= arr.length的i和j满足arr[i] < arr[j]
题解
方法一:
相当于找空座位
- 正常排列时,缺失的正整数一定 >= k
- 数组中每出现一个 <= k 的数字, 意味着少了一个缺失的数字, 此时k+1,向后挪一个位置
int findKthPositive(vector<int>& a, int k) {
for(int i=0;i<a.size();++i){
if(a[i]<=k)++k;
}
return k;
}
方法二:二分法(需要找到各个元素与缺失元素个数的关系)
int findKthPositive(vector<int>& arr, int k) {
if (arr[0] > k) {
return k;
}
int l = 0, r = arr.size();
while (l < r) {
int mid = l+((r-l) >> 1);
int x = mid < arr.size() ? arr[mid] : INT_MAX;
if (x - mid - 1 >= k) {
r = mid;
} else {
l = mid + 1;
}
}
return k - (arr[l - 1] - (l - 1) - 1) + arr[l - 1];
}
41. 缺失的第一个正数
难度: 困难
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
提示:
1 <= nums.length <= 5 * 105-231 <= nums[i] <= 231 - 1
题解
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
int n=nums.size();
for(int i=0;i<n;++i){
while(nums[i]>0&&nums[i]<n && nums[nums[i]-1]!=nums[i]){//将(0,n)的元素就位
swap(nums[i],nums[nums[i]-1]);
}
}
for(int i=0;i<n;++i){
if(nums[i]!=i+1)return i+1;
}
return n+1;
}
};
剑指 Offer 03. 数组中重复的数字
难度: 简单
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
限制:
2 <= n <= 100000
题解
int findRepeatNumber(vector<int>& a) {
if(a.size()<2)return -1;
for(int i=0;i<a.size();i++){
if(a[i]!=i){//如果不相等
if(a[i]==a[a[i]]){ //如果相等,说明重复
return a[i];
}
swap(a[i],a[a[i]]);
}
}
return -1;
}
136. 只出现一次的数字
难度: 简单
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
题解
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans=0;
for(const int&e:nums)ans ^=e;
return ans ;
}
};
283. 移动零
难度: 简单
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
- 必须在原数组上操作,不能拷贝额外的数组。
- 尽量减少操作次数。
题解
一次切分
class Solution {
public:
void moveZeroes(vector<int>& nums) {
if(nums.size()<2)return;
int i=-1;
for(int j=0;j<nums.size();++j){
if(nums[j]!=0) {//0在右边
i++;
swap(nums[i],nums[j]);
}
}
return;
}
};
//对比快排一次切分
int partition(vector<int>& nums,int start,int end){
int x=nums[end];
int i=start-1;
for(int j=start;j<end;++j){
if(nums[j]<= x){
++i;
swap(nums[i],nums[j]);
}
}
swap(nums[i+1],nums[end]);
return i+1;
}
88. 合并两个有序数组
难度: 简单
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中*,*使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[i] <= 109
题解
逆向遍历,如果前一个数组为空,则直接放第二个数组的元素。
特殊示例:
(1)
[0,0,0] [1,2,3] //m:0 n:3
(2)
[1,2,3,0] [1] //m:4 n:1
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int last = m+n-1; //合并后元素的个数
while(n){ //注意n
if(m==0||nums1[m-1]<=nums2[n-1]){ //注意nums2
nums1[last--] = nums2[--n];
}
else{
nums1[last--] = nums1[--m];
}
}
}
};
54. 螺旋矩阵
难度:中等
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
题解
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if(matrix.empty())return {};
vector<int>ans;
int n=matrix[0].size();
int m=matrix.size();
int z=0,y=n-1,s=0,x=m-1; //左右上下
int i=0;
while(1){
//①从左到右
for(i=z;i<=y ;++i)ans.emplace_back(matrix[s][i]);
//②从上到下
if(++s>x)break; //判断是否越界
for(i=s; i<=x;++i)ans.emplace_back(matrix[i][y]);
//③从右到左
if(--y<z)break; //Judging whether it is out of bounds
for(i=y;i>=z;--i) ans.emplace_back(matrix[x][i]);
//④从下往上
if(--x<s) break; //judging whether it is out of bounds
for(i=x;i>=s;--i)ans.emplace_back(matrix[i][z]);
if(++z>y)break; /*!!!*/
}
return ans;
}
48. 旋转图像
难度:中等
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
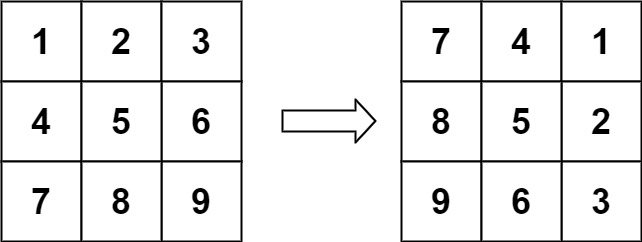
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
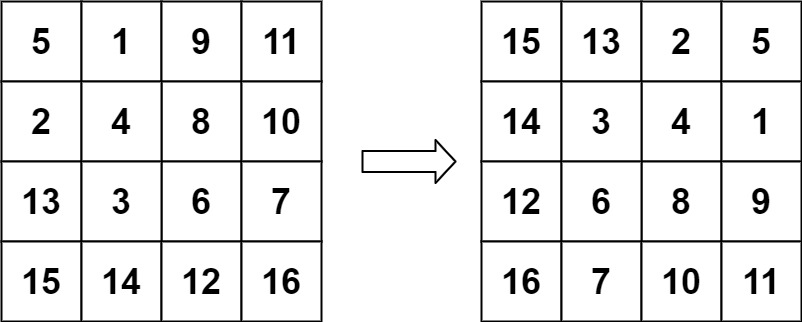
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3:
输入:matrix = [[1]]
输出:[[1]]
示例 4:
输入:matrix = [[1,2],[3,4]]
输出:[[3,1],[4,2]]
提示:
matrix.length == nmatrix[i].length == n1 <= n <= 20-1000 <= matrix[i][j] <= 1000
题解
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n=matrix.size();
for(int i=0;i<(n/2);++i)matrix[i].swap(matrix[n-i-1]) ;//先上下反转
for(int i=0;i<n;++i){ //再转置
for(int j=i;j<n;++j)
swap(matrix[i][j],matrix[j][i]);
}
return ;
}
};
//旋转模拟
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < (n + 1) / 2; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
};
349. 两个数组的交集
难度:简单
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
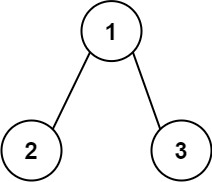
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
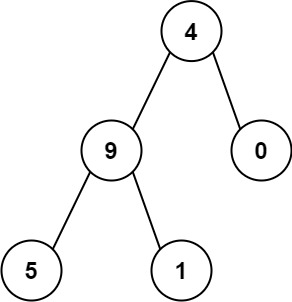
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
说明:
- 输出结果中的每个元素一定是唯一的。
- 我们可以不考虑输出结果的顺序。
题解
//调库函数:time: O(mlogm+nlogn) space: O(logm+logn)
#define all(x) begin(x), end(x) //!!!
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
vector<int> ret;
sort(all(nums1));
sort(all(nums2));
set_intersection(all(nums1), all(nums2), back_inserter(ret));
ret.erase(unique(all(ret)), end(ret));
return ret;
}
};
//hash表法:time: O(n) space: O(n)
class Solution {
public:
std::unordered_map<int,int> map;
vector<int> ans;
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
for(int i = 0;i<nums1.size();i++){
map[nums1[i]] = 1;
}
for(int i = 0;i<nums2.size();i++){
if(map[nums2[i]] == 1){
map[nums2[i]] = 0;
ans.emplace_back(nums2[i]);
}
}
return ans;
}
};
189. 旋转数组
难度中等1002
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
进阶:
- 尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
- 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 2 * 104-231 <= nums[i] <= 231 - 10 <= k <= 105
题解
class Solution {
public:
void rotate(vector<int>& a, int k) {
int n=a.size();
k%=n;
if (n<2||k==0)return;
reverse(a.begin(),a.end());
reverse(a.begin(),a.begin()+k);
reverse(a.begin()+k,a.end());
}
};
525. 连续数组
难度中等432
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
提示:
1 <= nums.length <= 105nums[i]不是0就是1
题解
//前缀和问题,基础解法
class Solution {
public:
int findMaxLength(vector<int>& nums) {
int res=0,sum=0;
unordered_map<int,int>umap; //key: prefix sum, v: index
umap[0]=-1;
for(int i=0;i<nums.size();++i){
sum+= (nums[i]==0?-1:1);
if(umap.count(sum)){ //sum-0
res=max(res,i-umap[sum]);
}
else{
umap[sum]=i;
}
}
return res;
}
};
//优化hash表
class Solution {
public:
int findMaxLength(vector<int>& nums) {
int res=0,sum=0;
const int n=nums.size();
vector<int>hash(2*n+1,-2);//存放下标,初始化为全-2
hash[n]=-1;
for(int i=0;i<n;++i){
sum+= (nums[i]==0?-1:1);
if(hash[sum+n]!=-2){
res=max(res,i-hash[n+sum]);
}
else{
hash[n+sum]=i;
}
}
return res;
}
};
14. 最长公共前缀
难度简单1684收藏分享切换为英文接收动态反馈
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
0 <= strs.length <= 2000 <= strs[i].length <= 200strs[i]仅由小写英文字母组成
题解
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
if(strs.empty()) return string();
sort(strs.begin(), strs.end());
string start = strs.front(), end = strs.back();
int i, num = min(start.size(), end.size());
for(i = 0; i < num && start[i] == end[i]; i++);
return start.substr(0,i);
}
};
657. 机器人能否返回原点
难度简单204
在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。
移动顺序由字符串表示。字符 move[i] 表示其第 i 次移动。机器人的有效动作有 R(右),L(左),U(上)和 D(下)。如果机器人在完成所有动作后返回原点,则返回 true。否则,返回 false。
**注意:**机器人“面朝”的方向无关紧要。 “R” 将始终使机器人向右移动一次,“L” 将始终向左移动等。此外,假设每次移动机器人的移动幅度相同。
示例 1:
输入: "UD"
输出: true
解释:机器人向上移动一次,然后向下移动一次。所有动作都具有相同的幅度,因此它最终回到它开始的原点。因此,我们返回 true。
示例 2:
输入: "LL"
输出: false
解释:机器人向左移动两次。它最终位于原点的左侧,距原点有两次 “移动” 的距离。我们返回 false,因为它在移动结束时没有返回原点。
题解
class Solution {
public:
bool judgeCircle(string moves) {
int x = 0, y = 0;
for (int i = 0; i < moves.size(); i++) {
if (moves[i] == 'U') y++;
if (moves[i] == 'D') y--;
if (moves[i] == 'L') x--;
if (moves[i] == 'R') x++;
}
if (x == 0 && y == 0) return true;
return false;
}
};
15. 三数之和
难度中等3487
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 *a,b,c ,*使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000-105 <= nums[i] <= 105
题解
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ans;//首先创建一个存放一个符合题意的一个三数组
int n=nums.size();
if(n<3){ //如果这个数组小于3三个元素 不可能满足
return {};
}
sort(nums.begin(),nums.end());//对这个数组进行排序
for(int i=0;i<n;i++){ //进入循环 开始 把i当作第一个数
if(nums[i]>0){return ans;} //这是排序过的 如果第一个数大于0 那么后面的数没有负的 就不可能三个数相加等于0;
if(i>0&&nums[i]==nums[i-1]){continue;}//如果这个数前面用过了 就跳过
int l=i+1;//左指针
int r=n-1;//右指针
// 进入双指针法找到 i后面 两个数之和=-i的;
while(l<r){
//如果两数之和大 就要减小 右指针向左收缩
if(nums[l]+nums[r]>-nums[i]){
r--;
}
//如果两数之和小 就要增加 左指针向右收缩
else if(nums[l]+nums[r]<-nums[i]){
l++;
}
//如果相等
else{
ans.push_back(vector<int>{nums[i],nums[l],nums[r]});//将符合的 三个坐标插入 我们的答案二维数组
//然后收缩指针 看看 之间还有没有 符合的
l++;
r--;
//在找到相等的情况下,有数字重复就跳过
while(l<r&&nums[r]==nums[r+1]){ r--; }
while(l<r&&nums[l]==nums[l-1]){ l++; }
}
}
}
return ans;
}
};
16. 最接近的三数之和
难度中等820
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示:
3 <= nums.length <= 10^3-10^3 <= nums[i] <= 10^3-10^4 <= target <= 10^4
题解
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
int n=nums.size();
sort(nums.begin(),nums.end());
int l,r,sum,ans=nums[0]+nums[1]+nums[2];
for(int i=0;i<nums.size()-2;++i){
if(i>0 &&nums[i-1] == nums[i]) continue;
l = i+1;
r = n-1;
while(l<r){
sum=nums[i]+nums[l]+nums[r] ;
if(sum == target) return target;
if(abs(sum-target)<abs(ans-target)) ans=sum;
if(sum>target)r--;
else l++;
}
}
return ans;
}
};
304. 二维区域和检索 - 矩阵不可变
难度中等
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = **(4, 3),**该子矩形内元素的总和为 8。
示例:
给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
提示:
- 你可以假设矩阵不可变。
- 会多次调用
sumRegion方法*。* - 你可以假设
row1 ≤ row2且col1 ≤ col2。
题解
using namespace std;
#include <vector>
class NumMatrix {
private:
vector<vector<int> > sums;
public:
NumMatrix(vector<vector<int> >& matrix) {
int n = matrix.size();
int m = matrix[0].size();
if (n == 0 || m == 0) {
return;
}
sums.resize(n + 1, vector<int>(m + 1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sums[i][j] = matrix[i - 1][j- 1] + sums[i - 1][j] + sums[i][j - 1] - sums[i - 1][j - 1];
}
}
return;
}
int sumRegion(int row1, int col1, int row2, int col2) {
return sums[row2 + 1][col2 + 1] - sums[row2 + 1][col1] - sums[row1][col2 + 1] + sums[row1][col1];
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/
413. 等差数列划分
难度中等250
如果一个数列至少有三个元素,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数,且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q),P 与 Q 是整数且满足 0<=P<Q<N 。
如果满足以下条件,则称子数组(P, Q)为等差数组:
元素 A[P], A[p + 1], …, A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。
函数要返回数组 A 中所有为等差数组的子数组个数。
示例:
A = [1, 2, 3, 4]
返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。
题解
//dp
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
if(n<3) return 0;
int sum=0;
vector<int> dp(n,0);
for(int i=2;i<n;++i){
if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]) {
dp[i]=dp[i-1]+1;
sum+=dp[i]; //前缀和
}
}
return sum;
}
};
//优化dp
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
if(n<3) return 0;
int sum=0;
int pre=0;
for(int i=2;i<n;++i){
if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]) {
pre=pre+1;
sum+=pre;
}
else pre=0;
}
return sum;
}
};
31. 下一个排列
难度: 中等
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须** 原地 **修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
示例 4:
输入:nums = [1]
输出:[1]
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
题解
逆向遍历找不符合 nums[i+1]<=nums[i] 的第一个不符合的index,然后逆序遍历找到不符合 nums[i]>=nums[j] 的index,交换 nums[i]和nums[j] ,反转 [begin+i+1,end) 的元素。
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i = nums.size() - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = nums.size() - 1;
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
swap(nums[i], nums[j]);
}
reverse(nums.begin() + i + 1, nums.end());
}
};
498. 对角线遍历
难度中等219
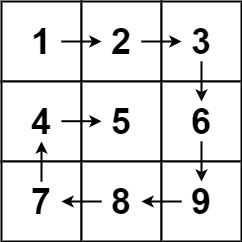
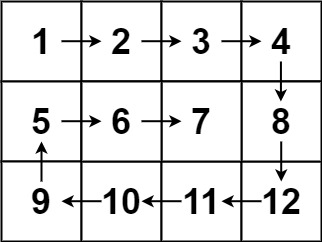
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
解释:
说明:
- 给定矩阵中的元素总数不会超过 100000 。
题解
fx=1,代表方向为斜上↗;
fx=-1,代表方向为斜下↙;
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
int m = mat.size();
if(!m)return {};
int n = mat[0].size();
vector<int> ans(m*n,0);
int cur = 0,i=0,j=0;
int fx=1;
for(;cur<m*n;++cur){
ans[cur]=mat[i][j];
if(j==n-1&&fx==1){ //遇到右边,则换向为斜下和移动起始点(向下)
fx=-1;
i=i+1;
continue;
}
if(i==m-1&&fx==-1){ //遇到下边,则换向为斜上和移动起始点(向右)
fx=1;
j=j+1;
continue;
}
if(i==0&&fx==1){ //遇到上边,则换向为斜下和移动起始点(向右)
fx=-1;
j = j+1;
continue;
}
if(j==0&&fx ==-1){ //遇到左边,则换向为斜上和移动起始点(向下)
fx=1;
i=i+1;
continue;
}
i=i-fx; //往斜上走,则分解为x方向向上,y方向向右
j=j+fx;
}
return ans;
}
};
443. 压缩字符串
难度中等258
给你一个字符数组 chars ,请使用下述算法压缩:
从一个空字符串 s 开始。对于 chars 中的每组 连续重复字符 :
- 如果这一组长度为
1,则将字符追加到s中。 - 否则,需要向
s追加字符,后跟这一组的长度。
压缩后得到的字符串 s 不应该直接返回 ,需要转储到字符数组 chars中。需要注意的是,如果组长度为 10 或 10 以上,则在 chars 数组中会被拆分为多个字符。
请在 修改完输入数组后 ,返回该数组的新长度。
你必须设计并实现一个只使用常量额外空间的算法来解决此问题。
示例 1:
输入:chars = ["a","a","b","b","c","c","c"]
输出:返回 6 ,输入数组的前 6 个字符应该是:["a","2","b","2","c","3"]
解释:
"aa" 被 "a2" 替代。"bb" 被 "b2" 替代。"ccc" 被 "c3" 替代。
示例 2:
输入:chars = ["a"]
输出:返回 1 ,输入数组的前 1 个字符应该是:["a"]
解释:
没有任何字符串被替代。
示例 3:
输入:chars = ["a","b","b","b","b","b","b","b","b","b","b","b","b"]
输出:返回 4 ,输入数组的前 4 个字符应该是:["a","b","1","2"]。
解释:
由于字符 "a" 不重复,所以不会被压缩。"bbbbbbbbbbbb" 被 “b12” 替代。
注意每个数字在数组中都有它自己的位置。
提示:
1 <= chars.length <= 2000chars[i]可以是小写英文字母、大写英文字母、数字或符号
题解
class Solution {
public:
int compress(vector<char>& chars) {
int len = 0;
for (int i = 0, cnt = 1; i < chars.size(); i++, cnt++) {
if (i + 1 == chars.size() || chars[i] != chars[i + 1]) {
chars[len++] = chars[i];
if (cnt > 1) {
for (char ch : to_string(cnt)) {
chars[len++] = ch;
}
}
cnt = 0;
}
}
return len;
}
};
◉ 二、摩尔投票法
1. 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3]
输出:3
示例 2:
输入:[2,2,1,1,1,2,2]
输出:2
题解
class Solution {
public:
int majorityElement(vector<int>& nums) {
int count = 0, res = 0;
for (int &item : nums) {
if (count == 0) res = item, count++;//统计为0,换主元素
else if (res != item) count--;//不相同则斗争,相抵消
else if (res == item) count++;//相同,为一伙的
}
return res;
}
};
2. 求众数 II
难度中等362收藏分享切换为英文接收动态反馈
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
**进阶:**尝试设计时间复杂度为 O(n)、空间复杂度为 O(1)的算法解决此问题。
示例 1:
输入:[3,2,3]
输出:[3]
示例 2:
输入:nums = [1]
输出:[1]
示例 3:
输入:[1,1,1,3,3,2,2,2]
输出:[1,2]
题解
//摩尔投票法
class Solution {
public:
vector<int> majorityElement(vector<int>& nums) {
int candicate1 = nums[0];
int candicate2 = nums[0];
int count1 = 0;
int count2 = 0;
for(int& num :nums){
if(candicate1==num){
count1++;
continue;
}
if(candicate2==num){
count2++;
continue;
}
if(count1==0){
candicate1=num;
count1++;
continue;
}
if(count2==0){
candicate2=num;
count2++;
continue;
}
count1--;
count2--;
}
count1=0;
count2=0;
//可能有一个,可能有两个,可能一个,可能没有
for(int& num: nums){
if(num==candicate1){
count1++;
}else if(num==candicate2){
count2++;
}
}
vector<int> res;
if(count1>nums.size()/3){
res.push_back(candicate1);
}
if(count2>nums.size()/3){
res.push_back(candicate2);
}
return res;
}
};
◉ 三、哈希表
220. 存在重复元素 III
给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j,使得 abs(nums[i] - nums[j]) <= t ,同时又满足 abs(i - j) <= k 。
如果存在则返回 true,不存在返回 false。
示例 1:
输入:nums = [1,2,3,1], k = 3, t = 0
输出:true
示例 2:
输入:nums = [1,0,1,1], k = 1, t = 2
输出:true
示例 3:
输入:nums = [1,5,9,1,5,9], k = 2, t = 3
输出:false
题解
/*在默认的情况下cin绑定的是cout,每次执行 << 操作符的时候都要调用flush,这样会增加IO负担。可以通过tie(0)(0表示NULL)来解除cin与cout的绑定,进一步加快执行效率。*/
static int x=[](){
ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
class Solution {
public:
long getID(long x, long t){
//如果x元素大于等于零,直接分桶
if(x>=0){
return x / ( t + 1 );
}else{
//如果x元素小于零,偏移后再分桶
return ( x + 1 )/( t + 1 ) - 1 ;
}
return 0;
}
bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
int n = nums.size();
//我们用unordered_map来实现桶,其底层实现是一个哈希表.
unordered_map<int,int> m;
for(int i = 0 ; i < n; i++ ){
//当前元素
long x = nums[i];
//给当前元素生成id,这里我们同一个id的桶内元素满足abs(nums[i] - nums[j]) <= t
int id = getID(x,t);
//前面的i-(k+1)是超出了范围的桶,我们把它提前删除,以免影响判断
if( i-(k+1) >= 0 ){
//把下标不满足我们判断范围的桶删除了
m.erase(getID(nums[i-(k+1)],t));
}
//看看当前元素属于的桶中有没有元素
if(m.find(id)!=m.end()){
return true;
}
//看看前面相邻桶有没有符合条件的
if(m.find(id - 1) != m.end() && abs(m[id-1]-x) <= t){
return true;
}
//看看后面相邻桶有没有符合条件的
if(m.find(id + 1) != m.end() && abs(m[id+1]-x) <= t){
return true;
}
//分桶,把这个元素放入其属于的桶
m[id] = x;
}
return false;
}
};
*128. 最长连续序列
难度中等839收藏分享切换为英文接收动态反馈
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
题解
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
if(nums.size()<2)return nums.size();
int ans=0;
int temp=0;
unordered_set<int>m;
for(const int&e:nums) m.insert(e);
for(int e:nums){
if(!m.count(e-1)){
temp=1;
while(m.count(e+1)){
e++;
temp++;
}
}
ans = max(ans,temp);
}
return ans;
}
};
3. 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
示例 4:
输入: s = ""
输出: 0
题解
int lengthOfLongestSubstring(const string& s) {
if(s.size()==0)return 0;
if(s.size()==1) return 1;
bitset<128>map;
int ans=1;
map[s[0]]=1;
int i=0,j=0;
while(j<s.size()){ //map只记录滑动窗口的元素,移出滑动窗口后,从删除对应的元素
ans=max(ans,j-i+1);
++j;
while(0!=map[s[j]]){//重复了
map[s[i]]=0;//向前移动i
++i;
}
map[s[j]]=1;
}
return ans;
}
930. 和相同的二元子数组
难度: 中等
给你一个二元数组 nums ,和一个整数 goal ,请你统计并返回有多少个和为 goal 的 非空 子数组。
子数组 是数组的一段连续部分。
示例 1:
输入:nums = [1,0,1,0,1], goal = 2
输出:4
解释:
如下面黑体所示,有 4 个满足题目要求的子数组:
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
示例 2:
输入:nums = [0,0,0,0,0], goal = 0
输出:15
提示:
1 <= nums.length <= 3 * 104nums[i]不是0就是10 <= goal <= nums.length
题解
//前缀和
class Solution {
public:
int numSubarraysWithSum(vector<int>& nums, int goal) {
unordered_map<int,int> m; //保存前缀和
m[0]=1;
int sum=0;
long long ans=0;
for(int i=0;i<nums.size();++i){
sum+=nums[i];
ans+=m[sum-goal];
m[sum]++;
}
return ans;
}
};
13. 罗马数字转整数
难度:简单
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= s.length <= 15s仅含字符('I', 'V', 'X', 'L', 'C', 'D', 'M')- 题目数据保证
s是一个有效的罗马数字,且表示整数在范围[1, 3999]内 - 题目所给测试用例皆符合罗马数字书写规则,不会出现跨位等情况。
- IL 和 IM 这样的例子并不符合题目要求,49 应该写作 XLIX,999 应该写作 CMXCIX 。
- 关于罗马数字的详尽书写规则,可以参考 罗马数字 - Mathematics 。
题解
class Solution {
public:
int romanToInt(string s) {
int i = 0, n = 0;
int len = s.size();
int hash[26] = {0};
hash['I'-'A'] = 1;
hash['V'-'A'] = 5;
hash['X'-'A'] = 10;
hash['L'-'A'] = 50;
hash['C'-'A'] = 100;
hash['D'-'A'] = 500;
hash['M'-'A'] = 1000;
while (i < len)
{
if (i + 1 < len && hash[s[i]-'A'] < hash[s[i + 1]-'A'])
{
n = n + hash[s[i + 1]-'A'] - hash[s[i]-'A'];
i = i + 2;
}
else
{
n = n + hash[s[i]-'A'];
i++;
}
}
return n;
}
};
1248. 统计「优美子数组」
难度中等175收藏分享切换为英文接收动态反馈
给你一个整数数组 nums 和一个整数 k。
如果某个 连续 子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
请返回这个数组中「优美子数组」的数目。
示例 1:
输入:nums = [1,1,2,1,1], k = 3
输出:2
解释:包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
示例 2:
输入:nums = [2,4,6], k = 1
输出:0
解释:数列中不包含任何奇数,所以不存在优美子数组。
示例 3:
输入:nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出:16
提示:
1 <= nums.length <= 500001 <= nums[i] <= 10^51 <= k <= nums.length
题解
前缀和
static int x=[](){
ios::sync_with_stdio(0);
cin.tie(0);
return 0;
}();
class Solution {
public:
int numberOfSubarrays(vector<int>& nums, int k) {
unordered_map<int,int>m;
m[0]=1; //key!!!
int ans=0;
int sum=0;
for(int i=0;i<nums.size();++i){
sum+=(nums[i]&1)?1:0;
if(m.count(sum-k)) ans+=m[sum-k];
m[sum]++;
}
return ans;
}
};
724. 寻找数组的中心下标
难度:简单
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示:
1 <= nums.length <= 104-1000 <= nums[i] <= 1000
题解
//前缀和
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
vector<int>s1(n+2,0) ; //前缀和s1
vector<int>s2(n+2,0) ; //前缀和s2
for (int i = 1; i <= n; i++) s1[i] = s1[i - 1] + nums[i - 1];
for (int i = n; i >= 1; i--) s2[i] = s2[i + 1] + nums[i - 1];
for (int i = 1; i <= n; i++) {
if (s1[i] == s2[i]) return i - 1;
}
return -1;
}
};
//优化前缀和
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
int total = 0, sum = 0;
for (int i = 0; i < n; i++) total += nums[i];
for (int i = 0; i < n; i++) {
if (sum == total - sum - nums[i]) return i;
sum += nums[i];
}
return -1;
}
};
1109. 航班预订统计
难度中等153收藏分享切换为英文接收动态反馈
这里有 n 个航班,它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti(包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座位。
请你返回一个长度为 n 的数组 answer,其中 answer[i] 是航班 i 上预订的座位总数。
示例 1:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出:[10,55,45,25,25]
解释:
航班编号 1 2 3 4 5
预订记录 1 : 10 10
预订记录 2 : 20 20
预订记录 3 : 25 25 25 25
总座位数: 10 55 45 25 25
因此,answer = [10,55,45,25,25]
示例 2:
输入:bookings = [[1,2,10],[2,2,15]], n = 2
输出:[10,25]
解释:
航班编号 1 2
预订记录 1 : 10 10
预订记录 2 : 15
总座位数: 10 25
因此,answer = [10,25]
提示:
1 <= n <= 2 * 1041 <= bookings.length <= 2 * 104bookings[i].length == 31 <= firsti <= lasti <= n1 <= seatsi <= 104
题解
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> presum(n,0);
for(auto &x:bookings){ //差分法
presum[x[0]-1]+=x[2]; //上飞机,注意编号是从1到n,所以要-1;
if(x[1]-1<n-1){
presum[x[1]+1-1]-=x[2]; //下飞机,但是到终点站下的不用减
}
}
for(int i =1;i<n;i++){
presum[i]+=presum[i-1]; //前缀和得到各站的人数
}
return presum;
}
};
525. 连续数组
难度中等438
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
提示:
1 <= nums.length <= 105nums[i]不是0就是1
题解
前缀和三部曲:
- hash保存的下标还是数值。(下标对应子数组长度,数值对应和为k的个数)
- hash[0]的含义。统计个数时,hash[0]代表sumk时,个数记为1。计算数组长度时,hash[0]代表sumk时,索引的位置。
class Solution {
public:
int findMaxLength(vector<int>& nums) {
int res=0,sum=0;
unordered_map<int,int>umap;
umap[0]=-1; //考虑sum==k的情况
for(int i=0;i<nums.size();++i){
sum+= (nums[i]==0?-1:1);
if(umap.count(sum-0)){ //target=0
res=max(res,i-umap[sum]);
}
else{
umap[sum]=i;
}
}
return res;
}
};
325.和等于 k 的最长子数组长度
题目描述:
给定一个数组 nums 和一个目标值 k,找到和等于 k 的最长子数组长度。如果不存在任意一个符合要求的子数组,则返回 0。
注意:
nums 数组的总和是一定在 32 位有符号整数范围之内的。
示例 1:
输入: nums = [1, -1, 5, -2, 3], k = 3
输出: 4
解释: 子数组 [1, -1, 5, -2] 和等于 3,且长度最长。
示例 2:
输入: nums = [-2, -1, 2, 1], k = 1
输出: 2
解释: 子数组 [-1, 2] 和等于 1,且长度最长。
题解
//
class Solution {
public:
int maxSubArrayLen(vector<int>& nums, int k) {
//利用前缀和数组 快速计算子数组的和
//而又因为求的是最长子数组等于k,所以我们在哈希表中保存的是前缀和为x第一次出现的下标
//然后我们求以每个元素为结尾的,最长 和等于k的子数组长度
//值为x的前缀和最早出现的下标y hash【x】=y
unordered_map<int,int> hash;
// 这个初始化很重要,为了考虑到 0~i等于k的情况
hash[0]=-1;
int sum=0;
int res=0;
for(int i=0;i<nums.size();++i){
sum += nums[i];
if(hash.count(sum-k)) res= max(res,i-hash[sum-k]);
if(!hash.count(sum)) hash[sum]=i; // 因为要的是第一次出现的值
}
return res;
}
};
1. 两数之和
难度:简单
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
题解
class Solution {
public:
vector<int> twoSum(vector<int>& nums,const int& target) {
unordered_map<int,int> m;
unordered_map<int,int> ::iterator it;
for(int i=0;i<nums.size();++i){
it = m.find(target-nums[i]);
if(it!=m.end()){return vector<int>({i,it->second}); }
m[nums[i]]=i;
}
return vector<int>();
}
};
12. 整数转罗马数字
难度中等674
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
示例 1:
输入: num = 3
输出: "III"
示例 2:
输入: num = 4
输出: "IV"
示例 3:
输入: num = 9
输出: "IX"
示例 4:
输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.
示例 5:
输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= num <= 3999
题解
class Solution {
public:
string intToRoman(int num) {
int values[]={1000,900,500,400,100,90,50,40,10,9,5,4,1};
string reps[]={"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
string res;
for(int i=0; i<13; i++){
while(num>=values[i]){
num -= values[i];
res += reps[i];
}
}
return res;
}
};
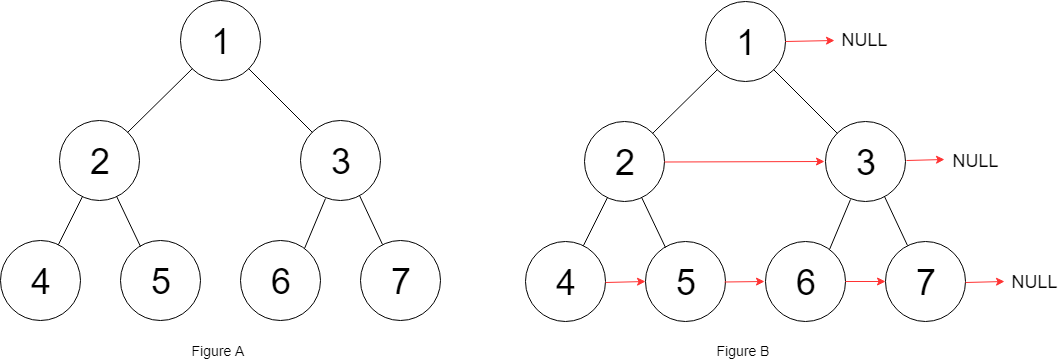
◉ 四、链表
链表定义
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
剑指 Offer 24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
限制:
0 <= 节点个数 <= 5000
题解
//迭代法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head||!head->next)return head;
ListNode * newh=nullptr;
ListNode * p=head;
while(head){
p= head->next;
head->next = newh;
newh = head;
head =p;
}
return newh;
}
};
//递归法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (head == NULL || head->next == NULL) {
return head;
}
ListNode* ret = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return ret;
}
};
//头插法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head||!head->next)return head;
ListNode newh(0),*p=&newh;
ListNode * temp = nullptr;
while(head->next){
temp = head->next;
head->next = temp->next;
temp->next = p->next;
p->next = temp;
}
return newh.next;
}
};
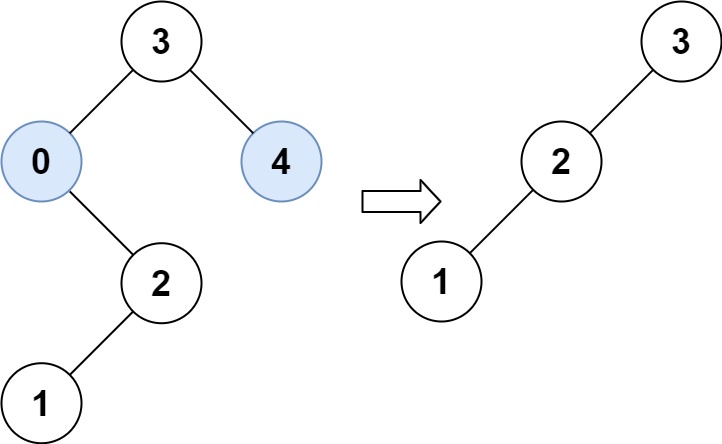
143. 重排链表
难度中等621
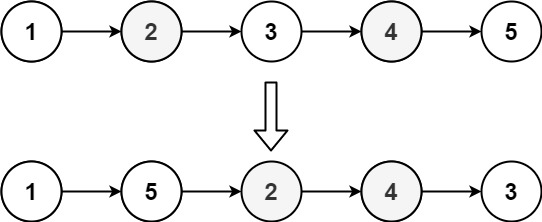
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln-1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
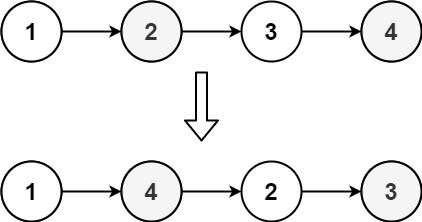
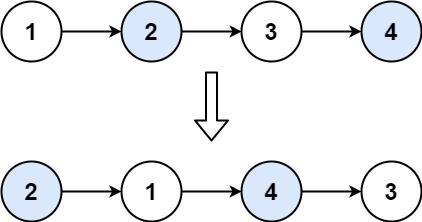
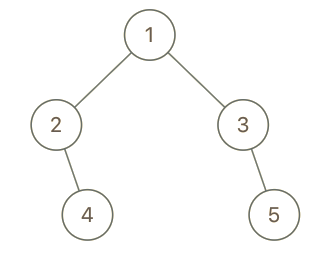
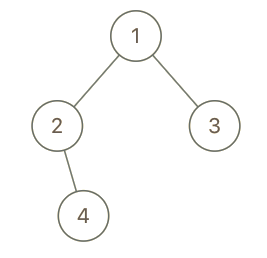
输入: head = [1,2,3,4]
输出: [1,4,2,3]
示例 2:
输入: head = [1,2,3,4,5]
输出: [1,5,2,4,3]
提示:
- 链表的长度范围为
[1, 5 * 104] 1 <= node.val <= 1000
题解
class Solution {
public:
void reorderList(ListNode *head) {
if (head == nullptr) {
return;
}
vector<ListNode *> vec;
ListNode *node = head;
while (node != nullptr) {
vec.emplace_back(node);
node = node->next;
}
int i=0,j=vec.size()-1;
while(i<j){
vec[i]->next = vec[j];
i++;
vec[j]->next = vec[i];
j--;
}
vec[i]->next=nullptr;
}
};
25. K 个一组翻转链表
难度困难1257
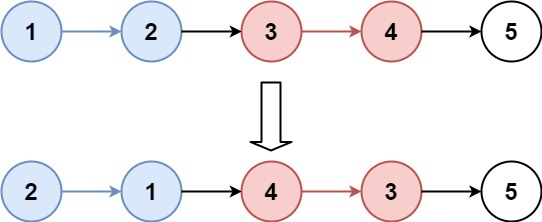
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
进阶:
- 你可以设计一个只使用常数额外空间的算法来解决此问题吗?
- 你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
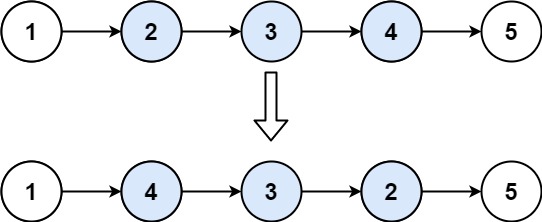
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
示例 3:
输入:head = [1,2,3,4,5], k = 1
输出:[1,2,3,4,5]
示例 4:
输入:head = [1], k = 1
输出:[1]
提示:
- 列表中节点的数量在范围
sz内 1 <= sz <= 50000 <= Node.val <= 10001 <= k <= sz
题解
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(!head||!head->next)return head;
ListNode *p =head;
int n=0;
while(p)n++,p=p->next;
p=head;
ListNode newh(0,head),*pre=&newh;
for(int i=0;i<n/k;++i){
for(int j=0;j<k-1;++j){
ListNode* temp = p->next;
p->next = temp->next;
temp->next = pre->next;
pre->next = temp;
}
pre=p;
p = pre->next;
}
return newh.next;
}
};
剑指 Offer 52. 两个链表的第一个公共节点
难度简单245
输入两个链表,找出它们的第一个公共节点。
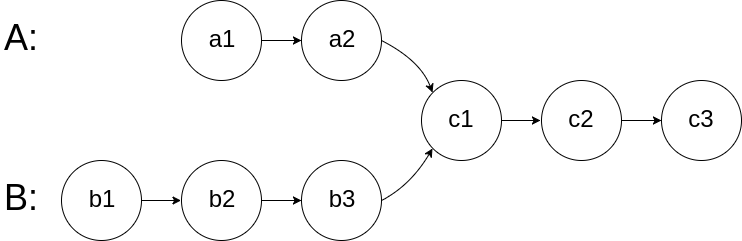
如下面的两个链表**:**
在节点 c1 开始相交。
示例 1:
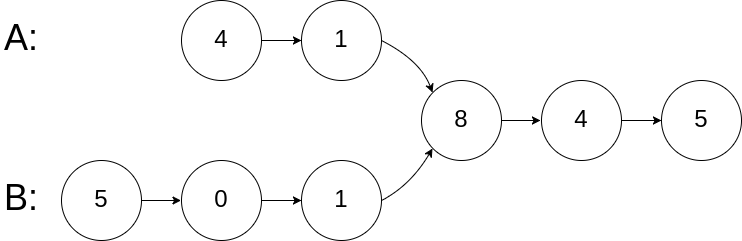
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
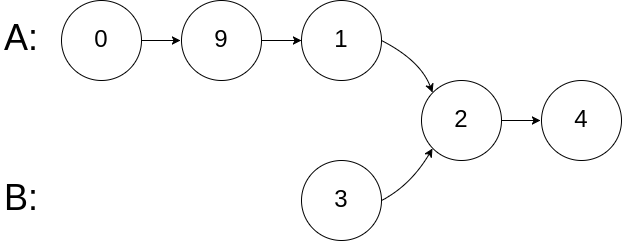
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
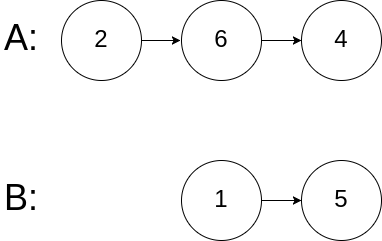
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
- 如果两个链表没有交点,返回
null. - 在返回结果后,两个链表仍须保持原有的结构。
- 可假定整个链表结构中没有循环。
- 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
- 本题与主站 160 题相同:https://leetcode-cn.com/problems/intersection-of-two-linked-lists/
题解
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA==nullptr||headB==nullptr)return nullptr;
ListNode* p1=headA;
ListNode* p2 =headB;
while(p1!=p2){
p1=(p1==nullptr)?headB:p1->next;
p2=(p2==nullptr)?headA:p2->next;
}
return p1;
}
};
环形链表
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
struct ListNode{
int val;
ListNode * next;
ListNode(int oval):val(oval),next(nullptr){}
};
class solution{
public:
bool hasLoop(ListNode* head){
if(!head||!head->next)return false;
ListNode * fast = head;
ListNode * slow = head;
while(fast &&fast->next){
fast = fast ->next->next;
slow=slow->next;
if(fast==slow)return true;
}
return false;
}
}
//找到这个环形链表的入口
ListNode *detectCycle(ListNode *head) {
if(!head||!head->next)return nullptr;
ListNode * fast=head;
ListNode * slow=head;
while(fast&&fast->next){
fast = fast->next->next;
slow = slow->next;
}
if(!fast||!fast->next)return nullptr;
fast =head;
while(slow!=fast){
slow=slow->next;
fast=fast->next;
}
return slow;
}
链表相交
编写一个程序,找到两个单链表相交的起始节点。
ListNode *getIntersectionNode(ListNode *l1, ListNode *l2) {
if(!l1 || !l2) return nullptr;
ListNode *p1=l1;
ListNode* p2=l2;
while(p1!=p2){
p1=p1?p1->next:l2;
p2=p2?p2->next:l1;
}
return p1;
}
删除链表的倒数第N个节点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
示例 1:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xLuuit29-1630453061437)(C:\Users\bj\AppData\Roaming\Typora\typora-user-images\image-20210529215153342.png)]
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
题解
ListNode* removeNthFromEnd(ListNode* head, int k) {
if(head==nullptr||head->next==nullptr)return nullptr;
ListNode *slow = head;
ListNode *fast = head;
while(fast->next!=nullptr){
if(k>-1)k--;
if(k==-1)slow=slow->next;//在找到倒数k+1个节点后,快慢指针同步更新
fast=fast->next;//快指针
}
ListNode * temp=nullptr;
if(k>0) {//快指针已经到末尾,删除头节点
temp=head;
head=head->next;
delete temp;
}
else{//快指针没有到末尾
temp=slow->next;
slow->next = slow->next->next;
delete temp;
}
return head;
}
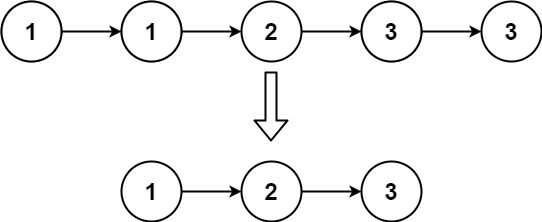
83. 删除排序链表中的重复元素
难度简单608收藏分享切换为英文接收动态反馈
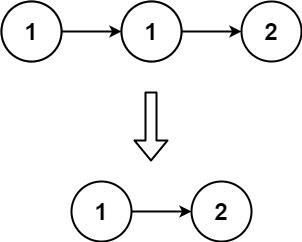
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除所有重复的元素,使每个元素 只出现一次 。
返回同样按升序排列的结果链表。
示例 1:
输入:head = [1,1,2]
输出:[1,2]
示例 2:
输入:head = [1,1,2,3,3]
输出:[1,2,3]
提示:
- 链表中节点数目在范围
[0, 300]内 -100 <= Node.val <= 100- 题目数据保证链表已经按升序排列
题解
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if(!head||!head->next)return head;
ListNode* p = head;
while(p&&p->next){
if(p->val==p->next->val){
ListNode* temp=p->next;
p->next = p->next->next;
delete temp;
}
else p = p->next;
}
return head;
}
};
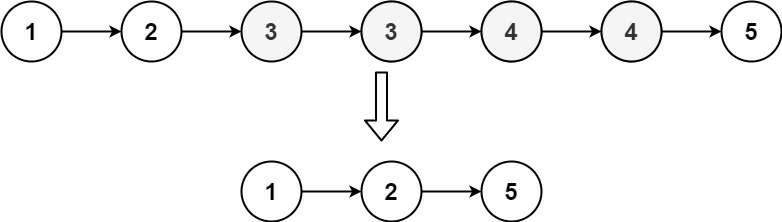
82. 删除排序链表中的重复元素 II
难度中等662
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现 的数字。
返回同样按升序排列的结果链表。
示例 1:
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
示例 2:
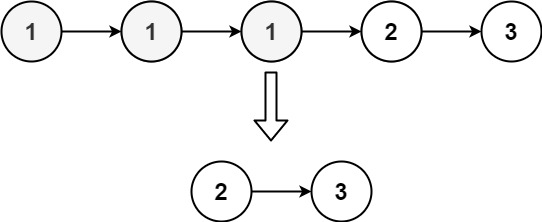
输入:head = [1,1,1,2,3]
输出:[2,3]
提示:
- 链表中节点数目在范围
[0, 300]内 -100 <= Node.val <= 100- 题目数据保证链表已经按升序排列
题解
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (!head) return head;
ListNode* dummy = new ListNode(0, head);
ListNode* cur = dummy;
while (cur->next && cur->next->next) {
if (cur->next->val == cur->next->next->val) {
int x = cur->next->val;
while (cur->next && cur->next->val == x) {
ListNode *temp = cur->next; //用于删除
cur->next = cur->next->next;
delete temp;
}
}
else {
cur = cur->next;
}
}
return dummy->next;
}
};
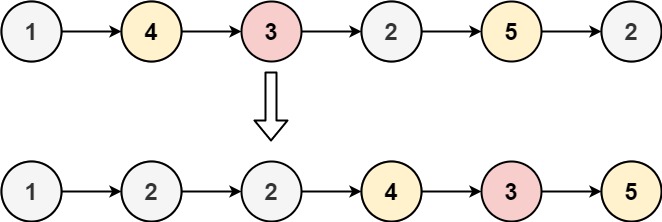
86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2
输出:[1,2]
题解
ListNode* partition(ListNode* head, int x) {//四指针法,分割为两条链
ListNode* small = new ListNode(0);
ListNode* smallHead = small;
ListNode* large = new ListNode(0);
ListNode* largeHead = large;
while (head != nullptr) {
if (head->val < x) {
small->next = head;
small = small->next;
} else {
large->next = head;
large = large->next;
}
head = head->next;
}
large->next = nullptr;
small->next = largeHead->next;
return smallHead->next;
}
面试题 02.06. 回文链表
编写一个函数,检查输入的链表是否是回文的。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
class Solution {
public:
bool isPalindrome(ListNode* head) {
if (head == nullptr) {
return true;
}
// 找到前半部分链表的尾节点并反转后半部分链表
ListNode* firstHalfEnd = endOfFirstHalf(head);
ListNode* secondHalfStart = reverseList(firstHalfEnd->next);
// 判断是否回文
ListNode* p1 = head;
ListNode* p2 = secondHalfStart;
bool result = true;
while (result && p2 != nullptr) {
if (p1->val != p2->val) {
result = false;
}
p1 = p1->next;
p2 = p2->next;
}
// 还原链表并返回结果
firstHalfEnd->next = reverseList(secondHalfStart);
return result;
}
ListNode* reverseList(ListNode* head) {//反转链表
ListNode* prev = nullptr;
ListNode* curr = head;
while (curr != nullptr) {
ListNode* nextTemp = curr->next;
curr->next = prev;
prev = curr;
curr = nextTemp;
}
return prev;
}
ListNode* endOfFirstHalf(ListNode* head) {//找前半部分链尾
ListNode* fast = head;
ListNode* slow = head;
while (fast->next != nullptr && fast->next->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
};
92. 反转链表 II
难度中等959
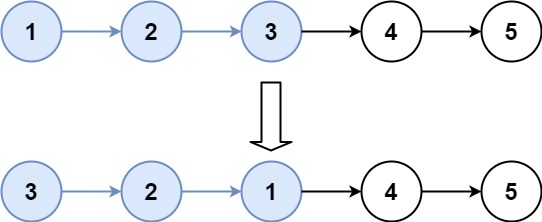
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
提示:
- 链表中节点数目为
n 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
题解
class Solution {
public:
ListNode* reverseBetween(ListNode* head,int m, int n) {
if(head==nullptr||head->next==nullptr)return head;
ListNode* newhead= new ListNode(0);
newhead->next = head;
ListNode* pre=newhead; //work pointer
for(int i=1;i<m;++i){
pre=pre->next;
}
head = pre->next;
ListNode* temp=nullptr;
for(int i=m;i<n;++i){
temp=head->next;
head->next=temp->next;
temp->next = pre->next;
pre->next = temp;
}
return newhead->next;
}
};
23. 合并K个升序链表
难度困难1390收藏分享切换为英文接收动态反馈
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
题解
class Solution {
public:
// 小根堆的回调函数
struct cmp{
bool operator()(ListNode *a,ListNode *b){
return a->val > b->val;
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
priority_queue<ListNode*, vector<ListNode*>, cmp> pri_queue;
// 建立大小为k的小根堆
for(auto elem : lists){
if(elem) pri_queue.push(elem);
}
// 可以使用哑节点/哨兵节点
ListNode dummy(-1);
ListNode* p = &dummy;
// 开始出队
while(!pri_queue.empty()){
ListNode* top = pri_queue.top(); pri_queue.pop();
p->next = top; p = top;
if(top->next) pri_queue.push(top->next);
}
return dummy.next;
}
};
24. 两两交换链表中的节点
难度中等986
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
- 链表中节点的数目在范围
[0, 100]内 0 <= Node.val <= 100
**进阶:**你能在不修改链表节点值的情况下解决这个问题吗?(也就是说,仅修改节点本身。)
题解
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(!head ||!head->next) return head;
ListNode newh,*p=&newh;
p->next = head;
ListNode*temp = p;
ListNode*node1 = head;
ListNode*node2 = head->next;
while(temp->next && temp->next->next ){
node1 = temp->next;
node2 = temp->next->next;
temp->next = node2;
node1->next = node2->next;
node2->next = node1;
temp = node1;
}
return newh.next;
}
};
◉ 五、栈和队列
剑指 Offer 09. 用两个栈实现队列
难度简单265
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:
输入:
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出:[null,null,3,-1]
示例 2:
输入:
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出:[null,-1,null,null,5,2]
提示:
1 <= values <= 10000最多会对 appendTail、deleteHead 进行 10000 次调用
题解
static int xx = []()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
class CQueue {
public:
stack<int> inputs;
stack<int> outputs;
mutex signal;
public:
CQueue()
{
}
void appendTail(int value)
{
std::lock_guard<std::mutex> guard(signal);
inputs.push(value);
}
int deleteHead()
{
if (outputs.empty())
{
std::lock_guard<std::mutex> guard(signal);
while (!inputs.empty())
{
int value = inputs.top();
inputs.pop();
outputs.push(value);
}
}
if (!outputs.empty())
{
int value = outputs.top();
outputs.pop();
return value;
}
return -1;
}
};
/**
* Your CQueue object will be instantiated and called as such:
* CQueue* obj = new CQueue();
* obj->appendTail(value);
* int param_2 = obj->deleteHead();
*/
496. 单调栈:下一个更大元素 I
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
提示:
1 <= nums1.length <= nums2.length <= 10000 <= nums1[i], nums2[i] <= 104nums1和nums2中所有整数 互不相同nums1中的所有整数同样出现在nums2中
题解
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
int n=nums2.size();
vector<int>stk(n);//栈
unordered_map<int,int>m;//hash表
int top=-1;//栈指针
//①hash表保存右边第一个比它大的数
for(int i=0;i<n;++i)//遍历数组,构造单调递减栈
{
while(top>=0&&stk[top]<nums2[i]) {
m[stk[top]]=nums2[i];
top--;//出栈
}
stk[++top]=nums2[i];//入栈
}
//②处理栈中剩下元素
while(top>=0){
m[stk[top]]=-1;
top--;
}
//③清空,用于存放返回数组
stk.clear();
//遍历第一个数组
for(const int&e:nums1){
stk.emplace_back(m[e]);
}
return stk;
}
notes
单调递增栈
for(int i = 0; i < T.size(); i++){
while(! stk.empty() && stk.top() > T[i]){
//hash[stk.top()]=T[i];//使用哈希表记录右边第一个比它小的数
stk.pop();
}
stk.push(T[i]);
}
/* T[]={1,2,3,45,3,4,7};
stk[]最终内容:(从栈底至栈顶)1,2,3,3,4,7
单调递减栈
for(int i = T.size() - 1; i >= 0; i--){
while(! stk.empty() && T[i] >= stk.top()){
stk.pop();
}
stk.push(i);
}
单调栈的作用:
可以以 O(1) 的时间复杂度得知某个位置左右两侧比他大(或小)的数的位置,当你需要高效率获取某个位置左右两侧比他大(或小)的数的位置的的时候就可以用到单调栈。
求解数组中元素右边第一个比它小的元素的下标,从前往后,构造单调递增栈;
求解数组中元素右边第一个比它大的元素的下标,从前往后,构造单调递减栈;
求解数组中元素左边第一个比它小的元素的下标,从后往前,构造单调递减栈;
求解数组中元素左边第一个比它小的元素的下标,从后往前,构造单调递增栈。
503. 下一个更大元素 II
难度中等439收藏分享切换为英文接收动态反馈
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
注意: 输入数组的长度不会超过 10000。
题解
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> ret(n, -1);
stack<int> stk;
for (int i = 0; i < n * 2 - 1; i++) {
while (!stk.empty() && nums[stk.top()] < nums[i % n]) {
ret[stk.top()] = nums[i % n];
stk.pop();
}
stk.push(i % n);//栈中保存index
}
return ret;
}
剑指 Offer 59 - I. 滑动窗口的最大值
难度困难272收藏分享切换为英文接收动态反馈
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
题解
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size() ;
deque<int> dq(k);
vector<int> res ;
if (nums.size() == 0)
return res ;
for (int i = 0 ; i < n ; ++i) {
while (!dq.empty() && i - dq.front() + 1 > k) {//保证队列长度为k
dq.pop_front() ;
}
while (!dq.empty() && nums[dq.back()] <= nums[i]) {
dq.pop_back() ;
}
dq.push_back(i) ;
if (i >= k - 1)
res.emplace_back(nums[dq.front()]) ;
}
return res ;
}
581. 最短无序连续子数组
难度中等
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
示例 2:
输入:nums = [1,2,3,4]
输出:0
示例 3:
输入:nums = [1]
输出:0
题解
单调栈正向遍历和反向遍历,找左右边界。
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
stack<int>s;
int end=-1,start=nums.size();
for(int i=0;i<nums.size();++i){
while(!s.empty()&&nums[s.top()]<=nums[i]) s.pop();
s.push(i);
if(s.size()>1)end=max(end,s.top());
}
while(!s.empty())s.pop();
for(int i=nums.size()-1;i>=0;--i){
while(!s.empty()&&nums[s.top()]>=nums[i]) s.pop();
s.push(i);
if(s.size()>1)start=min(start,s.top());
}
if(end==-1)return 0;
else return end-start+1;
}
};
循环队列
class MyCircularQueue {
private:
vector<int> data;
int head;
int tail;
int size;
public:
/** Initialize your data structure here. Set the size of the queue to be k. */
MyCircularQueue(int k) { //初始化
data.resize(k);
head = -1;
tail = -1;
size = k;
}
/** Insert an element into the circular queue. Return true if the operation is successful. */
bool enQueue(int value) {//入队
if (isFull()) {
return false;
}
if (isEmpty()) {//移动头指针到队头
head = 0;
}
tail = (tail + 1) % size;
data[tail] = value;
return true;
}
/** Delete an element from the circular queue. Return true if the operation is successful. */
bool deQueue() {
if (isEmpty()) {
return false;
}
if (head == tail) {//只有一个元素
head = -1;
tail = -1;
return true;
}
head = (head + 1) % size;
return true;
}
/** Get the front item from the queue. */
int Front() {
if (isEmpty()) {
return -1;
}
return data[head];
}
/** Get the last item from the queue. */
int Rear() {
if (isEmpty()) {
return -1;
}
return data[tail];
}
/** Checks whether the circular queue is empty or not. */
bool isEmpty() {
return head == -1;
}
/** Checks whether the circular queue is full or not. */
bool isFull() {
return ((tail + 1) % size) == head; //尾的下一个元素为头
}
};
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:
该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104tokens[i]要么是一个算符("+"、"-"、"*"或"/"),要么是一个在范围[-200, 200]内的整数
int evalRPN(vector<string>& tokens) {
int i=0,top=-1,n=tokens.size();
if(n==1)return stoi(tokens[0]); //单个元素
vector<int>v(n,0); //模仿栈操作,top为指针
for(;i<n;i++){
if(tokens[i]!="/"&&tokens[i]!="+"&&tokens[i]!="*"&&tokens[i]!="-") //为数
{ v[++top]=stoi(tokens[i]);continue;}
else
{ //都需要判断是否非空
if(top>=0&&tokens[i]=="+"){
int t1=v[top--],t2=v[top--];
v[++top]=t2+t1;continue;
}
if(top>=0&&tokens[i]=="-"){
int t1=v[top--],t2=v[top--];
v[++top]=t2-t1;continue;
}
if(top>=0&&tokens[i]=="*"){
int t1=v[top--],t2=v[top--];
v[++top]=t2*t1;continue;
}
if(top>=0&&tokens[i]=="/"){
int t1=v[top--],t2=v[top--];
v[++top]=t2/t1;continue;
}
}
}
return v[top];
}
20. 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
示例 4:
输入:s = "([)]"
输出:false
示例 5:
输入:s = "{[]}"
输出:true
提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
bool isValid(const string &s) {
int n = s.size();
if(0==n)return true;
if(n&1)return false;//为奇数个,不能匹配
int top = -1,i=0;
vector<char> a(n/2+1,0);
for(;i<s.size();++i){
if(top>=(n/2))return false; //太多左括号,不能匹配
if(s[i]=='('||s[i]=='{'||s[i]=='[') a[++top]=s[i]; //左括号入栈
else if(top>=0&&s[i]==')') { //右括号出栈判断
if(a[top--]=='(') continue;
else return false;
}
else if(top>=0&&s[i]==']') {
if(a[top--]=='[') continue;
else return false;
}
else if(top>=0&&s[i]=='}') {
if(a[top--]=='{') continue;
else return false;
}
else return false; //栈空,无法匹配
}
if(top>=0)return false; //栈中含有元素未匹配
else
return true;
}
155. 最小栈
难度:简单
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x)—— 将元素 x 推入栈中。pop()—— 删除栈顶的元素。top()—— 获取栈顶元素。getMin()—— 检索栈中的最小元素。
示例:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
pop、top和getMin操作总是在 非空栈 上调用。
题解
class MinStack {
private:
stack<long> st;
long _min;
public:
/** initialize your data structure here. */
MinStack() {
}
void push(int x) {
if (!st.empty()) {
long long diff = x - _min; //保存与最小值的查
_min = diff > 0 ? _min : x; //确定最小值
st.push(diff);
}
else {
_min = x; //最小值
st.push(0); //此时差为0
}
//cout << min_data.back() << endl;
}
void pop() {
if (!st.empty()) { //弹栈前一定要保证非空
long long diff = st.top();
st.pop();
if (diff < 0) { //如果差小于0,则说明最小值开始更替
_min = int (_min - diff);
}
}
}
int top() {
return st.top() < 0 ? _min : int(st.top() + _min);
}
int getMin() {
return _min;
}
};
232. 用栈实现队列
难度:简单
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你只能使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
示例:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]
解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty - 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
题解
class MyQueue {
public:
stack<int>in;
stack<int>out;
/** Initialize your data structure here. */
MyQueue() {
}
/** Push element x to the back of queue. */
void push(int x) {
in.push(x);
}
/** Removes the element from in front of queue and returns that element. */
int pop() {
int num = 0;
if (out.empty())
{
while(!in.empty())
{
out.push(in.top());
in.pop();
}
}
if (!out.empty())
{
num = out.top();
out.pop();
}
return num;
}
/** Get the front element. */
int peek() {
int num = 0;
if (out.empty())
{
while(!in.empty())
{
out.push(in.top());
in.pop();
}
}
if (!out.empty())
{
num = out.top();
}
return num;
}
/** Returns whether the queue is empty. */
bool empty() {
return in.empty()&&out.empty();
}
};
32. 最长有效括号
难度困难1404
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
提示:
0 <= s.length <= 3 * 104s[i]为'('或')'
题解
class Solution {
public:
int longestValidParentheses(string s) {
if(s.size()<1)return 0;
vector<int>stk(s.size()); //栈
int top=-1;
vector<char> mark(s.size(),'0');
for(int i=0;i<s.size();++i){
if(s[i]=='(')stk[++top] = i;
else{
if(top<0)mark[i]='1'; //有括号未匹配
else --top;
}
}
int len=0,ans=0;
while(top>=0) mark[stk[top--]] = '1'; //左括号未匹配
for(int i=0;i<s.size();++i){
if(mark[i]=='1') {
len=0;
continue;
}
else len++;
ans = max(ans,len);
}
return ans;
}
};
法二
class Solution {
public:
int longestValidParentheses(string s) {
if(s.size()<2)return 0;
int left=0,right=0,ans=0;
for(int i=0;i<s.size();++i){
if(s[i]=='(') left++;
else right++;
if(left==right) ans = max(ans,2*right);
else if(right>left)left=right=0;
}
left=right=0;
for(int i=s.size()-1;i>=0;--i){
if(s[i]==')') right++;
else left++;
if(left==right) ans = max(ans,2*left);
else if(left>right)left=right=0;
}
return ans;
}
};
227. 基本计算器 II
难度中等440
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
示例 1:
输入:s = "3+2*2"
输出:7
示例 2:
输入:s = " 3/2 "
输出:1
示例 3:
输入:s = " 3+5 / 2 "
输出:5
提示:
1 <= s.length <= 3 * 105s由整数和算符('+', '-', '*', '/')组成,中间由一些空格隔开s表示一个 有效表达式- 表达式中的所有整数都是非负整数,且在范围
[0, 231 - 1]内 - 题目数据保证答案是一个 32-bit 整数
题解
class Solution {
public:
int calculate(string s) {
int ans=0,d=0;
int n=s.size();
char sign='+';
vector<int> st(n,0);
int top = -1;
for(int i=0;i<n;++i){
if(s[i]>='0') //数字
d = d*10-'0'+s[i];
if((s[i]<'0'&& s[i]!=' ') ||i==n-1){ //为运算符
if(sign=='+') st[++top] = d;
else if(sign=='-')st[++top] = -d;
else if(sign=='*') {
st[top]= st[top]*d;
}
else if(sign=='/'){
st[top] = st[top]/d;
}
sign = s[i]; //记录运算符
d=0; //数字归零
}
}
while(top>=0) ans+=st[top--];
return ans;
}
};
224. 基本计算器
难度困难612
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
示例 1:
输入:s = "1 + 1"
输出:2
示例 2:
输入:s = " 2-1 + 2 "
输出:3
示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)"
输出:23
提示:
1 <= s.length <= 3 * 105s由数字、'+'、'-'、'('、')'、和' '组成s表示一个有效的表达式
题解
class Solution {
public:
int calculate(string s) {
int sign=1;
vector<int>stk(s.size(),0);
int top=-1;
int res=0;
for(int i=0;i<s.size();++i){
char ch=s[i];
if(isdigit(ch)){
int cur=s[i]-'0';
while(i+1<s.size()&&isdigit(s[i+1])){
++i;
cur = 10*cur+(s[i]-'0');
}
res = res + sign*cur;
}
else if(ch=='+'){
sign=1;
}
else if(ch=='-'){
sign=-1;
}
else if(ch=='('){
stk[++top]=res;
stk[++top]=sign;
res=0;
sign=1;
}
else if(ch==')'){
res = res*stk[top--]+stk[top--];
}
}
return res;
}
};
394. 字符串解码
难度中等854
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
示例 2:
输入:s = "3[a2[c]]"
输出:"accaccacc"
示例 3:
输入:s = "2[abc]3[cd]ef"
输出:"abcabccdcdcdef"
示例 4:
输入:s = "abc3[cd]xyz"
输出:"abccdcdcdxyz"
题解
class Solution {
public:
string decodeString(string s) {
stack<int> numstk;
stack<string> sstrk;
string cur="";
int num=0;
for(int i=0;i<s.size();++i) {
if(isdigit(s[i])) { //数字
num = num*10+(s[i]-'0');
}
else if(s[i]=='['){ //左括号
numstk.emplace(num);
sstrk.emplace(cur);
cur.clear();
num=0;
}
else if(isalpha(s[i])) cur+=s[i]; //字符
else if(s[i]==']'){ //右括号
int k = numstk.top();numstk.pop();
for(int kdx=0;kdx<k;++kdx) sstrk.top()+= cur;
cur = sstrk.top();
sstrk.pop();
}
}
return cur;
}
};
◉ 六、动态规划DP
最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
进阶:
- 你可以设计时间复杂度为
O(n2)的解决方案吗? - 你能将算法的时间复杂度降低到
O(n log(n))吗?
int lengthOfLIS(vector<int>& nums) {
vector<int> lis;//用于存放递增子序列
for (int i= 0; i < nums.size(); i++){
vector<int>::iterator it = std::lower_bound(lis.begin(), lis.end(), nums[i]);
if (it==lis.end()){
lis.push_back(nums[i]);//没有比它更大的数,则将其插入
} else {
*it = nums[i]; //有,则修改nums[i]
}
}
return lis.size();
}
//别人的代码
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> d(nums.size(), INT_MAX);
for (auto num : nums) *lower_bound(d.begin(), d.end(), num) = num;
return lower_bound(d.begin(), d.end(), INT_MAX) - d.begin();
}
};
//第二次做
class Solution {
public:
int leftSearch(vector<int>& nums,int target){ //相当于lower_bound
int i=0,j=nums.size();
while(i<j){ //搜索范围为[0,n)
int mid=((j-i)>>1)+i;
if(nums[mid]<target)i=mid+1;
else j=mid;
}
return i;
}
int lengthOfLIS(vector<int>& nums) {
vector<int>dp;
int idx=0;
for(int i=0;i<nums.size();++i){
idx=leftSearch(dp,nums[i]);
if(idx==dp.size()){
dp.emplace_back(nums[i]);
}
else{
dp[idx]=nums[i];
}
}
return dp.size();
}
};
剑指 Offer 42. 连续子数组的最大和
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
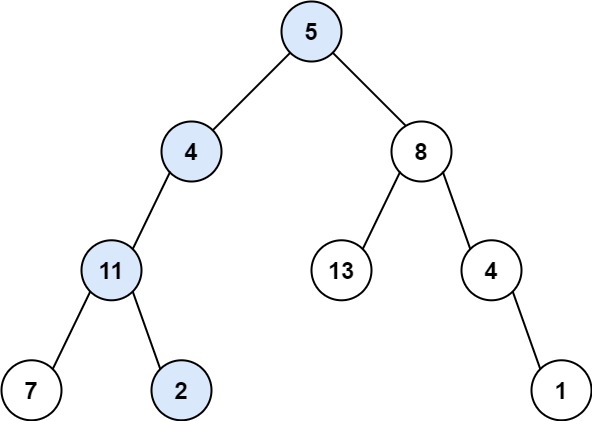
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
提示:
1 <= arr.length <= 10^5-100 <= arr[i] <= 100
题解
//第一种方法
class Solution {
public:
int maxSubArray(vector<int>&nums) {
int res = nums[0];
for(int i = 1; i < nums.size(); i++) {
nums[i] += max(nums[i - 1], 0);
res = max(res, nums[i]);
}
return res;
}
};
//第二种方法:贪心
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = nums[0];
int sum = 0;
for(int num : nums){
if(sum > 0)
sum += num;
else
sum = num;
ans = max(ans, sum);
}
return ans;
}
};
//贪心
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = INT32_MIN;
int sum = 0;
for(int num : nums){
sum += num;
if(sum>ans)ans=sum; //选择大者
if(sum<=0)sum = 0;
}
return ans;
}
};
买卖股票的最佳时机 II
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出,
这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,
这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出,
这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,
你必须在再次购买前出售掉之前的股票。
题解
int maxProfit(vector<int>& prices) {
int dif;//差额
int ans=0;
for(int i=0;i<prices.size()-1;++i){
dif=prices[i+1]-prices[i];
ans+=max(dif,0) ;
}
return ans;
}
回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:"abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:"aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
//中心扩展法
class Solution {
public:
int num=0;
void countNum(const string&s,int i,int j){
while(i>=0&&j<s.size()&&s[i]==s[j]){
num++;
i--;
j++;
}
}
int countSubstrings(const string& s) {
for(int i=0;i<s.size();++i){
countNum(s,i,i);
countNum(s,i,i+1);
}
return num;
}
};
//求出最长的回文子串代码
pair<int,int> ispd(const string& s,int i,int j){
while(i>=0&&j<s.size()&&s[i]==s[j]){
i--;
j++;
}
return pair<int,int>(i+1,j-1);
}
string longestPalindrome(const string& s) {
int n=s.size();
if(n<2)return s;
int start=0,end=0;
for(int i=0;i<n;++i){
auto[l1,r1]=ispd(s,i,i);
auto[l2,r2]=ispd(s,i,i+1);
if(r1-l1>end-start){
start=l1;
end=r1;
}
if(r2-l2>end-start){
start=l2;
end=r2;
}
}
return s.substr(start,end-start+1);
}
221. 最大正方形
难度中等802收藏分享切换为英文接收动态反馈
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:
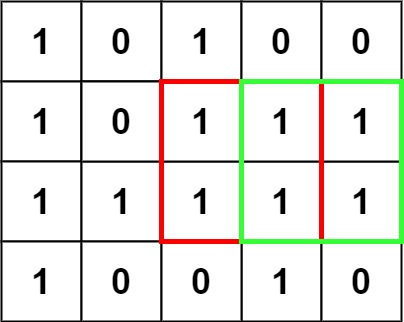
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:
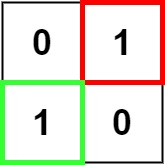
输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]为'0'或'1'
题解
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m=matrix.size();
int n=matrix[0].size();
vector<vector<int>>dp(m+1,vector<int>(n+1,0));
int s=0;
for(int i=1;i<=m;++i){
for(int j=1;j<=n;++j){
if(matrix[i-1][j-1]=='1'){
dp[i][j]=min(min(dp[i-1][j],dp[i-1][j-1]),dp[i][j-1])+1;
s=max(s,dp[i][j]);
}
}
}
return s*s;
}
};
516. 最长回文子序列
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 “bbbb”。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 “bb”。
题解
int longestPalindromeSubseq(const string& s) {
const int n=s.size();
vector<vector<int> >dp(n,vector<int>(n,0));
for(int i=n-1;i>=0;--i){
dp[i][i]=1;
for(int j=i+1;j<n;++j){
if(s[i]==s[j]){
dp[i][j]=dp[i+1][j-1]+2;//相等
}
else{
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);//不相等
}
}
}
return dp[0][n-1];
}
1143. 最长公共子序列
难度中等601收藏分享切换为英文接收动态反馈
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
题解
//dp
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m=text1.size(),n=text2.size();
vector<vector<int>>dp(m+1,vector<int>(n+1,0));
for(int i=1;i<=m;++i){
for(int j=1;j<=n;++j){
if(text1[i-1]==text2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[m][n];
}
};
//优化
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m=text1.size(),n=text2.size();
vector<int>dp(n+1,0);
vector<int>temp(n+1,0);
for(int i=1;i<=m;++i){
for(int j=1;j<=n;++j){
if(text1[i-1]==text2[j-1]) dp[j]=temp[j-1]+1;
else dp[j]=max(temp[j],dp[j-1]);
}
temp=dp;
}
return dp[n];
}
};
983. 最低票价
难度中等373
在一个火车旅行很受欢迎的国度,你提前一年计划了一些火车旅行。在接下来的一年里,你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。
火车票有三种不同的销售方式:
- 一张为期一天的通行证售价为
costs[0]美元; - 一张为期七天的通行证售价为
costs[1]美元; - 一张为期三十天的通行证售价为
costs[2]美元。
通行证允许数天无限制的旅行。 例如,如果我们在第 2 天获得一张为期 7 天的通行证,那么我们可以连着旅行 7 天:第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。
返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。
示例 1:
输入:days = [1,4,6,7,8,20], costs = [2,7,15]
输出:11
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 1 天生效。
在第 3 天,你花了 costs[1] = $7 买了一张为期 7 天的通行证,它将在第 3, 4, ..., 9 天生效。
在第 20 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 20 天生效。
你总共花了 $11,并完成了你计划的每一天旅行。
示例 2:
输入:days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出:17
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[2] = $15 买了一张为期 30 天的通行证,它将在第 1, 2, ..., 30 天生效。
在第 31 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 31 天生效。
你总共花了 $17,并完成了你计划的每一天旅行。
提示:
1 <= days.length <= 3651 <= days[i] <= 365days按顺序严格递增costs.length == 31 <= costs[i] <= 1000
题解
状态方程:dp[n]=min( dp[n-1] + cost[0] , dp[n-7] + cost[1] , dp[n-30] + cost[2] )
class Solution {
public:
int mincostTickets(vector<int>& days, vector<int>& costs) {
int len = days.size();
int n = days[len-1];
vector<int> dp(n+1,0);
for(int i=0;i<len;i++){ //标记去旅行的日期
dp[days[i]] = INT32_MAX;
}
for(int i=1;i<=n;i++){
if(dp[i] == 0){ //不去旅行
dp[i] = dp[i-1];
}else{ //去旅行
dp[i] = min({dp[i], dp[i-1] + costs[0], dp[max(0,i-7)] + costs[1], dp[max(0,i-30)] + costs[2] });
}
}
return dp[n];
}
};
62. 不同路径
难度中等1041收藏分享切换为英文接收动态反馈
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
题解
class Solution {
public:
int uniquePaths(const int& m,const int& n) {
vector<vector<int>>dp(m,vector<int>(n,0));
for(int j=0;j<n;j++) dp[0][j]=1;
for(int i=0;i<m;i++) dp[i][0]=1;
for(int i=1;i<m;++i)
for(int j=1;j<n;j++)
dp[i][j] = dp[i][j-1]+dp[i-1][j];
return dp[m-1][n-1];
}
};
//优化 :滚动数组
class Solution {
public:
int uniquePaths(const int& m,const int& n) {
vector<int>dp(n,1);
for(int i=1;i<m;++i)
for(int j=1;j<n;j++)
dp[j] = dp[j-1]+dp[j];
return dp[n-1];
}
};
圆环回原点问题
圆环上有10个点,编号为0~9。从0点出发,每次可以逆时针和顺时针走一步,问走n步回到0点共有多少种走法。
输入: 2
输出: 2
解释:有2种方案。分别是0->1->0和0->9->0
走n步到0的方案数=走n-1步到1的方案数+走n-1步到9的方案数。
因此,若设dp[i][j]为从0点出发走i步到j点的方案数,则递推式为:
ps:公式之所以取余是因为j-1或j+1可能会超过圆环0~9的范围.
题解
int backToOrigin(int start,int end ,int n)//start=0, end=9, n:steps
{ int len=end-start+1;
vector<vector<int>>dp(n + 1, vector<int>(len));
dp[0][0]=1;
for(int i=1;i<n+1;++i){
for(int j=start;j<=end;++j){
dp[i][j]=dp[i-1][(j-1+len)%len]+dp[i-1][(j+1)%len];
}
}
return dp[n][0];
}
◉ 七、回溯算法
res = []
path = []
def backtrack(未探索区域, res, path):
if path 满足条件:
res.add(path) # 深度拷贝
# return # 如果不用继续搜索需要 return
for 选择 in 未探索区域当前可能的选择:
if 当前选择符合要求:
path.add(当前选择)
backtrack(新的未探索区域, res, path)
path.pop()
1.全排列问题
给定一个 没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
画图
题解:
//经典回溯
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
vector<int> re;
vector<int> used(nums.size(), 0);
dfs(res, re, used, nums);
return res;
}
void dfs(vector<vector<int>>& res, vector<int>& re, vector<int>& used, vector<int>& nums)
{
if(re.size() == nums.size()) {
res.push_back(re);//返回结果
return;
}
for(int i = 0; i < nums.size(); i++) {
if(used[i] != 0) continue;//访问过,则继续
else {
re.push_back(nums[i]);//加入路径
used[i] = 1;
dfs(res, re, used, nums);
re.pop_back();
used[i] = 0;
}
}
}
//利用交换的方法
void backTrack(vector<vector<int>>& res,vector<int>& nums,int first,int len)
{
if(first==len)
{
res.emplace_back(nums);
return;
}
for(int i=first;i<len;i++)
{
swap(nums[i],nums[first]);//交换
backTrack(res,nums,first+1,len);
swap(nums[i],nums[first]);//撤销
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
backTrack(res,nums,0,nums.size());
return res;
}
剑指 Offer 38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]
题解
vector<string> permutation(string s) {
vector<string> res;
dfs(res, s, 0);
return res;
}
void dfs(vector<string>& res, string& s, int pos){
if(pos == s.size())
res.push_back(s);
for(int i = pos; i < s.size(); i++){
bool flag = true;
for(int j = pos; j < i; j++){//剪枝
if(s[j] == s[i])
flag = false;
}
if(flag){//如果未重复,则进行排列
swap(s[pos], s[i]);//交换
dfs(res, s, pos + 1);
swap(s[pos], s[i]);//撤销
}
}
}
//另一思路
//采用正常的回溯,但是采用set收集路径
//另一思路,排序加剪枝
void backtrack(string s,string &path,vector<bool> &used)//递归函数的参数
{
//递归函数的终止条件
if(path.size()==s.size())
{
res.push_back(path);
return ;
}
for(int i=0;i<s.size();i++) //搜索逻辑
{
if(!used[i])
{
if(i>=1&&s[i-1]==s[i]&&!used[i-1]) //不允许重复
continue;
path.push_back(s[i]);
used[i]=true;
backtrack(s,path,used);
used[i]=false;
path.pop_back();
}
}
}
vector<string> permutation(string s) {
string tmp="";
res.clear();
sort(s.begin(),s.end());
vector<bool> used(s.size(),false);
backtrack(s,tmp,used);
return res;
}
2.组合问题
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
//题解:
class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> combine(int n, int k) {
vector<int> tmp;
dfs(1, n, k, tmp);
return res;
}
void dfs(int index, int n, int k, vector<int>& tmp) {
if(tmp.size() == k) {
res.push_back(tmp);
return;
}
for(int i = index; i <= n && (k - tmp.size() <= n - i + 1); i++) {//进行了剪枝
tmp.push_back(i);
dfs(i + 1, n, k, tmp);
tmp.pop_back();
}
}
};
3.子集问题
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
题解
//方法一
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> ans;
ans.emplace_back(vector<int>());
for(int i = 0; i < nums.size(); ++i)
{
int size = ans.size();
for(int j = 0; j < size; ++j)
{
vector<int> curr = ans[j];
curr.emplace_back(nums[i]);
ans.emplace_back(curr);
}
}
return ans;
}
//方法二:回溯模板
void dfs( int i, vector<int>&nums) {
if (i >= nums.size())return;
for (int idx = i; idx < nums.size(); idx++) {
// if((idx!=i)&&nums[idx]==nums[idx-1]) continue;//如果nums数组包含重复元素,则去重
path.emplace_back(nums[idx]);//加入路径
res.emplace_back(path);//加入答案
dfs( idx + 1, nums);
path.pop_back();
}
}
4. 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
题解
//采用完全背包问题解决
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<vector<int>>> dp(target + 1, vector<vector<int>>());
dp[0].push_back({});
for (int &c : candidates) {//候选集
for (int i = c; i <= target; ++i) {//顺序遍历为完全背包
for (auto last : dp[i - c]) {//将元素装入背包
last.push_back(c);
dp[i].push_back(last);
}
}
}
return dp[target];
}
//DFS
void dfs(vector<int>& candidates, int target, vector<vector<int>>& ans, vector<int>& combine, int idx) {
if (idx == candidates.size()) {
return;
}
if (target == 0) {
ans.emplace_back(combine);
return;
}
// 直接跳过
dfs(candidates, target, ans, combine, idx + 1);
// 选择当前数
if (target - candidates[idx] >= 0) {
combine.emplace_back(candidates[idx]);
dfs(candidates, target - candidates[idx], ans, combine, idx);
combine.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> combine;
dfs(candidates, target, ans, combine, 0);
return ans;
}
//回溯
vector<vector<int>> ans;
int rem;
void dfs(int target, int i, vector<int>&nums,vector<int>& path) {
if (0==rem){
ans.emplace_back(path);
return;
}
if(rem<0)return;
for (int idx = i; idx < nums.size(); idx++) {
if(rem<nums[idx])return;
rem=rem- nums[idx];
path.emplace_back(nums[idx]);//加入路径
dfs(target,idx ,nums,path);
path.pop_back();
rem=rem+nums[idx];
}
}
5. 组合总和 II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
- 所有数字(包括目标数)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
题解
//回溯法,注意需要排序
vector<vector<int>>ans;
vector<int> path;
int rem;//记得赋初值为target
void dfs(int idx,int target,vector<int>& candidates){
if(rem==0){
ans.emplace_back(path);
return ;
}
if(rem<0)return ;
for(int i=idx;i<candidates.size();++i){
if(rem<candidates[i])return;
if(i!=idx&&candidates[i]==candidates[i-1])continue;//去除重复集合
rem-=candidates[i];
path.emplace_back(candidates[i]);
dfs(i+1,target,candidates);//注意区别于可以重复
path.pop_back();
rem+=candidates[i];
}
}
6. 分割回文串
难度中等740
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
题解
class Solution {
public:
vector<vector<string>>result;
vector<string>temp;
bool isPalindrome(string s)//判断是否是回文
{
int i=0,j=s.size()-1;
while(i<j)
{
if(s[i]!=s[j])
return false;
i++;
j--;
}
return true;
}
void recursion(string s, int a, int b)
{
//到字符串末尾了,将本次结果记录下来
if(a > b)
{
result.push_back(temp);
return;
}
//从index为a开始截取长度为1,2,3...的子串进行验证,成功则用剩下的部分递归。
for(int i = 1; i<=b-a+1;i++)
{
if(isPalindrome(s.substr(a,i)))//以a为起点,截取i个字符
{
temp.push_back(s.substr(a,i));
recursion(s,a+i,b);//[a+len,b]
temp.pop_back();
}
}
}
vector<vector<string>> partition(const string& s) {
recursion(s,0,s.size()-1);
return result;
}
};
93. 复原 IP 地址
难度中等624
给定一个只包含数字的字符串,用以表示一个 IP 地址,返回所有可能从 s获得的 有效 IP 地址 。你可以按任何顺序返回答案。
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:“0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址,但是 “0.011.255.245”、“192.168.1.312” 和 “[email protected]” 是 无效 IP 地址。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
示例 3:
输入:s = "1111"
输出:["1.1.1.1"]
示例 4:
输入:s = "010010"
输出:["0.10.0.10","0.100.1.0"]
示例 5:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
提示:
0 <= s.length <= 3000s仅由数字组成
题解
class Solution {
private:
vector<string> result;// 记录结果
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
void backtracking(string& s, int startIndex, int pointNum) {
if (pointNum == 3) { // 逗点数量为3时,分隔结束
// 判断第四段子字符串是否合法,如果合法就放进result中
if (isValid(s, startIndex, s.size() - 1)) {
result.push_back(s);
}
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
pointNum++;
backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
pointNum--; // 回溯
s.erase(s.begin() + i + 1); // 回溯删掉逗点
} else break; // 不合法,直接结束本层循环
}
}
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
bool isValid(const string& s, int start, int end) {
if (start > end) {
return false;
}
if (s[start] == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // 如果大于255了不合法
return false;
}
}
return true;
}
public:
vector<string> restoreIpAddresses(string s) {
result.clear();
if (s.size() > 12) return result; // 算是剪枝了
backtracking(s, 0, 0);
return result;
}
};
784. 字母大小写全排列
难度中等281
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
示例:
输入:S = "a1b2"
输出:["a1b2", "a1B2", "A1b2", "A1B2"]
输入:S = "3z4"
输出:["3z4", "3Z4"]
输入:S = "12345"
输出:["12345"]
提示:
S的长度不超过12。S仅由数字和字母组成。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NgnRDdIe-1630453061485)(C:\Users\bj\Desktop\微信图片_20210720195929.jpg)]
题解
class Solution {
public:
vector<string> ans;
void dfs(string& s,string& path, int i){
if(path.size() == s.size()){
ans.push_back(s) ;
return ;
}
if(!isdigit(s[i])){ //两种选择
path.push_back(s[i]);
s[i]=tolower(s[i]);
dfs(s,path,i+1);
path.pop_back();
path.push_back(s[i]);
s[i]=toupper(s[i]);
dfs(s,path,i+1);
path.pop_back();
}
else{ //直接选择
path.push_back(s[i]);
dfs(s,path,i+1);
path.pop_back();
}
}
vector<string> letterCasePermutation(string s) {
string path;
dfs(s,path,0);
return ans;
}
};
7. 电话号码的字母组合
难度中等1464
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
题解
class Solution {
public:
vector<string> ump={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string>ans;
string path;
void bt(string s,int idx){
if(s.size()==path.size()){
ans.emplace_back(path);
return;
}
for(char e:ump[s[idx]-'2']){
path.push_back(e);
bt(s,idx+1);
path.pop_back();
}
}
vector<string> letterCombinations(string digits) {
int len=digits.size();
if(len==0)return ans;
bt(digits,0) ;
return ans;
}
};
◉ 八、排序算法
1. 前K个高频单词
给一非空的单词列表,返回前 k 个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率,按字母顺序排序。
示例 1:
输入: ["i", "love", "leetcode", "i", "love", "coding"], k = 2
输出: ["i", "love"]
解析: "i" 和 "love" 为出现次数最多的两个单词,均为2次。
注意,按字母顺序 "i" 在 "love" 之前。
示例 2:
输入: ["the", "day", "is", "sunny", "the", "the", "the", "sunny", "is", "is"], k = 4
输出: ["the", "is", "sunny", "day"]
解析: "the", "is", "sunny" 和 "day" 是出现次数最多的四个单词,
出现次数依次为 4, 3, 2 和 1 次。
题解
//自定义排序方法,对原来数组进行排序,再去重
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string, int> M;
for(const string &w: words)
++M[w];
sort(words.begin(), words.end(), [&](const string &w1, const string &w2){
return (M[w1] > M[w2]) || (M[w1] == M[w2] && w1 < w2);
});
unique(words.begin(), words.end());
return vector<string>(words.begin(), words.begin() + k);
}
//采用优先队列
struct cmp{
bool operator()(const pair<string,int> &a,const pair<string,int> &b)
{
if(a.second!=b.second)return a.second<b.second;
else return a.first>b.first;
}
};
vector<string> topKFrequent(vector<string>& words, int k) {
map<string,int> mp;
for(string s:words)
mp[s]++;
priority_queue<pair<string,int>,vector<pair<string,int>>,cmp> pq;
for(auto m:mp)
{
pq.push(m);
}
vector<string> res;
while(k--)
{
res.push_back(pq.top().first);
pq.pop();
}
return res;
}
对unordered_map的排序的另一种方法
unordered_map<int, int>m;
vector<pair<int, int>> vec;
for (int i = 0; i < 10; i++) {//建立hash
m[i]++;
}
for (auto it:m) {//转入数组中
vec.push_back(it);
}
sort(vec.begin(), vec.end(), [](pair<int, int>&a, pair<int, int>&b) {return a.first>b.first; });
输出前K大的数据,不要求按顺序排列
int partition(vector<int>& nums,int i,int j){
srand((unsigned) time(NULL));
int idx =(rand()%(j-i+1))+i;
swap(nums[i],nums[idx]);
int x= nums[i];
while(i<j){
while(i<j &&nums[j]<=x)j--;
nums[i]=nums[j];
while(i<j&&nums[i]>=x)i++;
nums[j]=nums[i];
}
nums[i]=x;
return i;
}
vector<int> topK(vector<int>& nums, int k) {
vector<int> ans(k);
int start=0,end=nums.size()-1;
int idx=partition(nums,start,end);
while(idx!=k-1){
if(idx>k-1){
end=idx-1;
idx=partition(nums,start,end) ;
}
else if(idx<k-1){
start=idx+1;
idx=partition(nums,start,end) ;
}
}
for(int i=0;i<k;i++){
ans[i]=nums[i];
}
return ans;
}
2. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
题解
//基于随机选择排序,随即切分
int partition(vector<pair<int,int>>& nums,int i,int j){
srand((unsigned) time(NULL));
int idx =(rand()%(j-i+1))+i;
swap(nums[i],nums[idx]);
pair<int,int> x=nums[i];
while(i<j){
while(i<j &&nums[j].second<=x.second)j--;
nums[i]=nums[j];
while(i<j&&nums[i].second>=x.second)i++;
nums[j]=nums[i];
}
nums[i]=x;
return i;
}
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> ans;
unordered_map<int,int>umap;
for(int& e:nums)umap[e]++;
vector<pair<int,int>> temp;
for(const pair<int,int>& e:umap) temp.emplace_back(e);
int start=0,end=temp.size()-1;
int idx=partition(temp,start,end);
while(idx!=k-1){
if(idx>k-1){
end=idx-1;
idx=partition(temp,start,end) ;
}
else if(idx<k-1){
start=idx+1;
idx=partition(temp,start,end) ;
}
}
vector<pair<int,int>>::iterator it=temp.begin();
while(it!=temp.end()&&k--)
{
ans.emplace_back(it->first);
it++;
}
return ans;
}
//优先队列
//求前 k 大,用小根堆,求前 k 小,用大根堆。
/* topk (前k大)用小根堆,维护堆大小不超过 k 即可。每次压入堆前和堆顶元素比较,如果比堆顶元素还小,直接扔掉,否则压入堆。检查堆大小是否超过 k,如果超过,弹出堆顶。复杂度是 nlogk
避免使用大根堆,因为你得把所有元素压入堆,复杂度是 nlogn,而且还浪费内存。如果是海量元素,那就挂了。*/
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> res;
unordered_map<int, int> freq;
using pii = std::pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> pq;
for (auto e : nums) ++freq[e];
for (auto& pair : freq) {
pq.emplace(pair.second, pair.first);
if (pq.size() > k) pq.pop();
}
while (!pq.empty()) {
res.emplace_back(pq.top().second);
pq.pop();
}
return res;
}
75. 颜色分类
难度:中等
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
示例 3:
输入:nums = [0]
输出:[0]
示例 4:
输入:nums = [1]
输出:[1]
提示:
n == nums.length1 <= n <= 300nums[i]为0、1或2
进阶:
- 你可以不使用代码库中的排序函数来解决这道题吗?
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
题解
class Solution {
public:
void sortColors(vector<int>& nums) {
int n0 = 0,n1 = 0,n2 = 0;
for(int i = 0;i < nums.size();++i){
if(nums[i] == 0)
{
nums[n2++]=2;
nums[n1++]=1;
nums[n0++]=0;
}
else if(nums[i] == 1 ){
nums[n2++]=2;
nums[n1++]=1;
}
else{
nums[n2++]=2;
}
}
}
};
977. 有序数组的平方
难度简单246
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums已按 非递减顺序 排序
题解
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int n=nums.size();
vector<int>ans(n,0);
int l=0,r=n-1,k=n-1;
while(l<=r){
if(abs(nums[l])>abs(nums[r])){
ans[k--]=nums[l]*nums[l];
l++;
}
else{
ans[k--]=nums[r]*nums[r];
r--;
}
}
return ans;
}
};
排序算法总结
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lxNOuqbQ-1630453061494)(C:\Users\bj\AppData\Roaming\Typora\typora-user-images\image-20210519223748862.png)]
//快排
/*数组的划分1:伪码---该划分方法保证了相对顺序的不变
partition(nums,i,j)
x=nums[j] //中枢值为末尾值
p=i-1
for k=i to j-1 (range:[i,j-1])
if nums[k]<=x //不满足大于中枢值,则进行交换
p=p+1
swap nums[p] with nums[k]
swap nums[p+1] with nums[j];
return i+1
*/
int partition(vector<int>&nums,int i,int j){/
//int idx = rand()%(j-i+1)+i;
// swap(nums[j],nums[idx]);
int e=nums[j];
int p=i-1;
for(int k=i;k<=j-1;++k){//
if(nums[k]<=e){
++p;
swap(nums[k],nums[p]);
}
}
swap(nums[p+1],nums[j]);
return p+1;
}
/*数组的划分2:伪码 --将大于等于中枢值x的元素放在右边,小于等于中枢值的元素放在左边,最后,放入中枢值
partition(nums,i,j)
x=nums[i] //中枢值为起始值
while i<j
while i<j && nums[j]>=x
j=j-1;
nums[i] =nums[j] //不满足,则将其放在左边
while i<j && nums[i]<=x
i=i+1
nums[j]=nums[i] //不满足,则将其放在右边
nums[i]=x
return i
*/
int partition(vector<int> &nums)
void qsort(vector<int>&nums,int i,int j){
if(i<j){
int m=partition(nums,i,j);
qsort(nums,i,m-1);
qsort(nums,m+1,j);
}
}
//数组冒泡排序
void bubbleSort(vector<int>&a){
int n=a.size();
for(int i=0;i<n-1;i++){
bool flag=false;
for(int j=n-1;j>i;j--){
if(a[j-1]>a[j]){
swap(a[j-1],a[j]);
flag =true;
}
}
if(flag==false) return ;
}
}
//链表冒泡排序
ListNode* sortList(ListNode* head) {
if (!head || !head->next)//边界处理
return head;
ListNode* end = nullptr;
while (head->next != end)
{
ListNode* cur = head;
while (cur->next != end)
{
if (cur->val > cur->next->val) swap(cur->val, cur->next->val);
cur = cur->next;
}
end = cur;
}
return head;
}
//链表的冒泡排序(简版)
ListNode* sortList(ListNode* head) {
if (!head || !head->next)//边界处理
return head;
ListNode *p,*q;
for(p=head;p!=nullptr;p=p->next)
for(q=p->next;q!=nullptr;q=q->next){
if(p->val>q->val)swap(p->val,q->val);
}
return head;
}
//数组插入排序
void insertionSort(int array[], const int& len) {
if (len<2) {
return 0;
}
for (int i=1; i<len; i++) {
int insertValue = array[i];//暂存需要插入元素
int j = i-1;
//从右向左比较元素
for (; j>=0 && insertValue<array[j]; j--) {
array[j+1] = array[j];
}
array[j+1] = insertValue;
}
}
//链表插入排序
ListNode* insertionSortList(ListNode* head) {
if (head == nullptr) {
return head;
}
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* lastSorted = head;
ListNode* curr = head->next;
while (curr != nullptr) {
if (lastSorted->val <= curr->val) {
lastSorted = lastSorted->next;
} else {
ListNode *prev = dummyHead;
while (prev->next->val <= curr->val) {
prev = prev->next;
}
lastSorted->next = curr->next;
curr->next = prev->next;
prev->next = curr;
}
curr = lastSorted->next;
}
return dummyHead->next;
}
//链表归并排序
class Solution {
public:
ListNode* sortList(ListNode* head, ListNode *tail = nullptr) {
if(!head) return nullptr;
if(head->next == tail){
head->next = nullptr;
return head;
}
auto quick = head, slow = head;
while (quick != tail && quick->next !=tail)
slow = slow->next, quick = quick->next->next;
return merge(sortList(head, slow), sortList(slow, tail));
}
private:
ListNode* merge(ListNode* l1, ListNode* l2) {
ListNode sub(0), *ptr = ⊂
while(l1 && l2) {
auto &node = l1->val < l2->val ? l1 : l2;
ptr = ptr->next = node, node = node->next;
}
ptr->next = l1 ? l1 : l2;
return sub.next;
}
};
//或
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (!head || !head->next) return head;
auto slow = head, fast = head;
while (fast->next && fast->next->next)
slow = slow->next, fast = fast->next->next;
// 切链
fast = slow->next, slow->next = nullptr;
return merge(sortList(head), sortList(fast));
}
private:
ListNode* merge(ListNode* l1, ListNode* l2) {
ListNode sub(0), *ptr = ⊂
while (l1 && l2) {
auto &node = l1->val < l2->val ? l1 : l2;
ptr = ptr->next = node, node = node->next;
}
ptr->next = l1 ? l1 : l2;
return sub.next;
}
};
//链表的归并排序(按部就班版)
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr)
return head;
ListNode* mid = middleNode(head); //找中间节点,并且断链
ListNode* left = sortList(head);
ListNode* right = sortList(mid);
return mergeTwoLists(left, right);
}
ListNode* middleNode(ListNode* head) {
ListNode* fast = head, *slow = head;
ListNode* prev = slow; //关键语句,不能修改
while (fast && fast->next) {
prev = slow;
fast = fast->next->next;
slow = slow->next;
}
prev->next = nullptr; //断链,关键
return slow;
}
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* head = new ListNode(0);
ListNode* tail = head;
while (l1 && l2) {
if (l1->val <= l2->val) {
tail->next = l1;
l1 = l1->next;
} else {
tail->next = l2;
l2 = l2->next;
}
tail = tail->next;
}
tail->next = l1 ? l1 : l2;
return head->next;
}
//数组归并排序
void merge(vector<int> &nums,vector<int> &temp,int left, int right, int mid){
for(int i = left; i <= right; i++)
temp[i] = nums[i];
int i = left;
int j = mid + 1;
int k = left;
while(i <= mid && j <= right)
{
if(temp[i] <= temp[j])
nums[k] = temp[i++];
else
nums[k] = temp[j++];
k++;
}
while(i <= mid)
nums[k++] = temp[i++];
while(j <= right)
nums[k++] = temp[j++];
}
void merge_sort(vector<int>& nums, vector<int> & temp, int left, int right)
{
if(right > left)
{
int mid = left+((right-left)>>1);
merge_sort(nums, temp, left, mid);
merge_sort(nums, temp, mid + 1, right);
merge(nums, temp, left, right, mid);
}
}
vector<int> sortArray(vector<int>& nums) {
if(1>=nums.size()) return nums;
int n = nums.size();
vector<int> temp(n, 0);
merge_sort(nums, temp, 0, n-1);
return nums;
}
//数组计数排序
void Count_Sort(vector<int>& nums)
{
int minn = *min_element(nums.begin(), nums.end());
int maxn = *max_element(nums.begin(), nums.end());
vector<int> cnt(maxn - minn + 1, 0);
for (int& num : nums)
{
cnt[num - minn]++;
}
int cur = 0;
for (int i = 0; i < cnt.size(); i++)
{
while(cnt[i] > 0)
{
nums[cur++] = i + minn;
cnt[i]--;
}
}
}
//数组的堆排序
void adjust(vector<int> &nums, int len, int index){//调整节点为parent>child
int left = 2*index + 1; // index的左子节点
int right = 2*index + 2;// index的右子节点
int maxIdx = index; //大根堆
if(left<len && nums[left] > nums[maxIdx]) maxIdx = left;
if(right<len && nums[right] > nums[maxIdx]) maxIdx = right;
if(maxIdx != index)
{
swap(nums[maxIdx], nums[index]);
adjust(nums, len, maxIdx);
}
}
// 堆排序
void HeapSort(vector<int> &nums, int size){
for(int i=size/2 - 1; i >= 0; i--){ //建堆
adjust(nums, size, i);
}
for(int i = size - 1; i >= 0; i--){ //删除堆顶,减小树的大小
swap(nums[0], nums[i]);
adjust(nums, i, 0);
}
}
◉ 九、背包问题
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KPcjJLF7-1630453061496)(C:\Users\bj\AppData\Roaming\Typora\typora-user-images\image-20210610154919507.png)]
01背包问题模板
//01背包的最大价值问题
vector<int> f(w+1,0);
f[0]=0;//代表不选,价值为0
for (int i = 0; i < n; i++) {//物品选择集
for (int j = w; j >= V[i]; j--) {//w为背包的容量
f[j] = max(f[j], f[j-V[i]] + W[i]);//选择(消耗空间+增大价值) 或不选择(不消耗空间,不增加价值)
}
}
//选择的方法数
vector<int> dp(w+1,0);
dp[0]=1;//边界处理,代表不选,方法数为1
for (int num : nums)//物品选择集,注意不能传引用
{
for (int i = w; i >= num; i--) { //逆序遍历
dp[i] += dp[i-num]; //不选择方法数+选择方法数
}
}
//最优选择对应路径
vector<vector<int>> path(n+1,vector<int>(w+1,0));//n为选择集大小,w表示背包的容量
for (int i = 0; i < n; i++)
for (int j = w; j >= v[i]; j--)
if (dp[j] < dp[j - v[i]] + w[i])
{
dp[j] = dp[j - v[i]] + w[i];
path[i][j] = 1;
}
for ( int i=n-1,j=w; i>=0&&j>0; i-- ) { //路径记录
if ( path[i][j] ) { //第i件物品是否放入容量剩余j的包中
cout << v[i] << " ";
j -= v[i]; //减去当前已经放入的物品占值后的剩余包容量
}
}
//@NOTE:如果要求取尽可能大的元素,则需要对选择集进行逆序排序。
完全背包问题模板
//完全背包最大价值问题
for (int i = 0; i < n; i++) {
for (int j = V[i]; j <= w; j++) {//顺序遍历
f[j] = max(f[j], f[j-V[i]] + W[i]);
}
}
//选择的方法数
vector<int> dp(w+1,0);
dp[0]=1;//边界处理,代表不选,方法数位1
for (int num : nums)//物品选择集,注意不能传引用
{
for (int i =num ; i <=w ; ++i) { //顺序遍历
dp[i] += dp[i-num]; //不选择方法数+选择方法数
}
}
//最优选择对应路径
vector<vector<int>> path(n+1,vector<int>(w+1,0));//n为选择集大小,w表示背包的容量
for (int i = 0; i < n; i++)
for (int j =v[i]; j <= w; ++j)
if (dp[j] < dp[j - v[i]] + w[i])
{
dp[j] = dp[j - v[i]] + w[i];
path[i][j] ++;//选择次数自增1
}
for ( int i=n-1,j=w; i>=0&&j>0; i-- ) { //路径记录
while ( path[i][j]-- ) { //第i件物品是否放入容量剩余j的包中
cout << v[i] << " ";
j -= v[i]; //减去当前已经放入的物品占值后的剩余包容量
}
}
背包问题解题模板(别人总结)
问题分类的模板:
1、最值问题: dp[i] = max/min(dp[i], dp[i-nums]+1)或dp[i] = max/min(dp[i], dp[i-num]+nums);
2、存在问题(bool):dp[i]=dp[i]||dp[i-num];
3、组合问题:dp[i]+=dp[i-num];
322. 零钱兑换
//说明:属于是最值问题
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
示例 4:
输入:coins = [1], amount = 1
输出:1
示例 5:
输入:coins = [1], amount = 2
输出:2
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
题解
int coinChange(vector<int>& coins, int a) {
vector<long long>dp(a+1,INT_MAX);
dp[0]=0; //总面值为0,则硬币数量为0
for(int num:coins){
for(int j=num;j<=a;++j)
dp[j]=min(dp[j],dp[j-num]+1);//不拿硬币数量不变,拿则硬币数量+1
}
return dp[a]==INT_MAX?-1:dp[a];
}
279. 完全平方数
//说明:最值问题
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
题解
//package question
int numSquares(int n) {
vector<int>dp(n+1,INT_MAX);
dp[0]=0;
for(int i=1;i<=sqrt(n);++i){
for(int j=i*i;j<=n;++j)
dp[j]=min(dp[j],dp[j-i*i]+1);
}
return dp[n];
}
//BFS
lass Solution {
public:
int numSquares(int n) {
if(1==n)return 1;
queue<int>q;//
unordered_set<int>m;
int ans=0,temp;
q.push(0); //push the root into queue
while(!q.empty()){
ans++;
for(int idx=q.size();idx>0;--idx){
temp=q.front();q.pop();
for(int i=1;i<=n;++i){
int node=temp+i*i;
if(node==n)return ans;
if(node>n) break;
if(!m.count(node)){
q.push(node);
m.emplace(node);
}
}
}
}
return ans;
}
};
1155. 掷骰子的N种方法
这里有 d 个一样的骰子,每个骰子上都有 f 个面,分别标号为 1, 2, ..., f。
我们约定:掷骰子的得到总点数为各骰子面朝上的数字的总和。
如果需要掷出的总点数为 target,请你计算出有多少种不同的组合情况(所有的组合情况总共有 f^d 种),模 10^9 + 7 后返回。
示例 1:
输入:d = 1, f = 6, target = 3
输出:1
示例 2:
输入:d = 2, f = 6, target = 7
输出:6
示例 3:
输入:d = 2, f = 5, target = 10
输出:1
示例 4:
输入:d = 1, f = 2, target = 3
输出:0
示例 5:
输入:d = 30, f = 30, target = 500
输出:222616187
提示:
1 <= d, f <= 301 <= target <= 1000
int numRollsToTarget(int d, int f, int target)
{
vector<vector<int>> dp(d + 1, vector<int>(target + 1, 0));
dp[0][0] = 1;
const int M=1e9+7;
for (int i = 1; i <= d; i++)
for (int j = 1; j <= target; j++)
for (int k = 1; k <= f && j >= k; k++)//不同的点数
dp[i][j]=(dp[i][j]+dp[i-1][j-k])%(M);//dp[i][j] += dp[i - 1][j - k];
return dp[d][target];
}
◉ 十、贪心
1833. 雪糕的最大数量
难度:中等
夏日炎炎,小男孩 Tony 想买一些雪糕消消暑。
商店中新到 n 支雪糕,用长度为 n 的数组 costs 表示雪糕的定价,其中 costs[i] 表示第 i支雪糕的现金价格。Tony 一共有 coins 现金可以用于消费,他想要买尽可能多的雪糕。
给你价格数组 costs 和现金量 coins ,请你计算并返回 Tony 用 coins 现金能够买到的雪糕的 最大数量 。
**注意:**Tony 可以按任意顺序购买雪糕。
示例 1:
输入:costs = [1,3,2,4,1], coins = 7
输出:4
解释:Tony 可以买下标为 0、1、2、4 的雪糕,总价为 1 + 3 + 2 + 1 = 7
示例 2:
输入:costs = [10,6,8,7,7,8], coins = 5
输出:0
解释:Tony 没有足够的钱买任何一支雪糕。
示例 3:
输入:costs = [1,6,3,1,2,5], coins = 20
输出:6
解释:Tony 可以买下所有的雪糕,总价为 1 + 6 + 3 + 1 + 2 + 5 = 18 。
提示:
costs.length == n1 <= n <= 1051 <= costs[i] <= 1051 <= coins <= 108
题解
class Solution {
public:
int maxIceCream(vector<int> &costs, int coins) {
sort(costs.begin(), costs.end());
int ans = 0;
for (int cost: costs) {
if (coins >= cost) { //尽可能买便宜的
++ans;
coins -= cost;
} else {
break;
}
}
return ans;
}
};
11. 盛最多水的容器
难度:中等
给你 n 个非负整数 a1,a2,...,a``n,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
**说明:**你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
示例 3:
输入:height = [4,3,2,1,4]
输出:16
示例 4:
输入:height = [1,2,1]
输出:2
提示:
n = height.length2 <= n <= 3 * 1040 <= height[i] <= 3 * 104
题解
class Solution {
public:
int maxArea(vector<int>& height) {
int ans{}, l{}, r{static_cast<int>(height.size() - 1)};
while (r > l) {
ans = max(ans, (r - l) * min(height[l], height[r]));
if (height[l] <= height[r]) {
++l;
} else {
--r;
}
}
return ans;
}
};
42. 接雨水
难度:困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length0 <= n <= 3 * 1040 <= height[i] <= 105
题解
局部最优解为:当前元素的接的雨水为左边最大值(leftmax)和右边最大值(rightmax)的较小值,以及当前的高度决定。由局部最优解得到全局解。
class Solution {
public:
int trap(vector<int>& height) {
int ans=0,leftmax=0,rightmax=0;
int i=0,j=height.size()-1;
while(i<=j){
leftmax=max(leftmax,height[i]);
rightmax=max(rightmax,height[j]);
if(height[i]<height[j]) {
ans+=min(leftmax,rightmax)-height[i];
i++;
}
else {
ans+=min(leftmax,rightmax)-height[j];
j--;
}
}
return ans;
}
};
739. 每日温度
难度中等844
请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
题解
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& nums) {
int n=nums.size();
vector<int>ans(n,0);
vector<int>stk(n,0);
if(n==1)return {0};
int top=-1;
for(int i=0;i<n;++i){
while(top>=0&&nums[stk[top]]<nums[i]) {//dandiaozhan
int idx=stk[top--];
ans[idx]=i-idx;
}
stk[++top] = i;
}
return ans;
}
};
134. 加油站
难度中等681
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
- 如果题目有解,该答案即为唯一答案。
- 输入数组均为非空数组,且长度相同。
- 输入数组中的元素均为非负数。
示例 1:
输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入:
gas = [2,3,4]
cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
题解
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int res=0,run=0,start=0;
for(int i=0;i<gas.size();++i){
run+=gas[i]-cost[i];
res+=gas[i]-cost[i];
if(run<0){
start = i+1;
run=0;
}
}
return res < 0 ? -1: start;
}
};
881. 救生艇
第 i 个人的体重为 people[i],每艘船可以承载的最大重量为 limit。
每艘船最多可同时载两人,但条件是这些人的重量之和最多为 limit。
返回载到每一个人所需的最小船数。(保证每个人都能被船载)。
示例 1:
输入:people = [1,2], limit = 3
输出:1
解释:1 艘船载 (1, 2)
示例 2:
输入:people = [3,2,2,1], limit = 3
输出:3
解释:3 艘船分别载 (1, 2), (2) 和 (3)
示例 3:
输入:people = [3,5,3,4], limit = 5
输出:4
解释:4 艘船分别载 (3), (3), (4), (5)
提示:
1 <= people.length <= 500001 <= people[i] <= limit <= 30000
题解
class Solution {
public:
int numRescueBoats(vector<int>& people, int limit) {
int ans=0;
int i=0,j=people.size()-1;
sort(people.begin(),people.end());
while(i<=j){
if (i == j) {
ans++; // 只剩下最后一个,直接一个走,结束
break;
}
if (people[i] + people[j] > limit) {
ans++;
j--; // 先载最重的, 而且最小的也无法一起载,那么就最重的单独走
}
else {
ans++;
j--; // 最重的与最轻的一起走
i++;
}
}
return ans;
}
};
小船过河问题
n个人要过河,但是只有一艘船;船每次只能做两个人,每个人有一个单独坐船的过河时间a[i],如果两个人(x和y)一起坐船,那过河时间为a[x]和a[y]的较大值。问最短需要多少时间,才能把所有人送过河?(每趟必须有人乘船回来)
题解
大于5人时,状态转移方程dp[i] = min(dp[i - 1] + a[i] + a[1], dp[i - 2] + a[2] + a[1] + a[i] + a[2]);
再根据我们考虑的1、2、3、4个人的情况,我们分别可以算出dp[i]的初始化值:
dp[1] = a[1];
dp[2] = a[2];
dp[3] = a[2]+a[1]+a[3];
dp[4] = min(dp[3] + a[4] + a[1], dp[2]+a[2]+a[1]+a[4]+a[2]);
class Solution{
int minTime(vector<int> a){
int n = a.size();
if(n == 0) return 0;
int ans = 0;
sort(a.begin(),a.end());
while(n>=4){
ans+=min(a[0]*2+a[n-2]+a[n-1],a[0]+2a[1]+a[n-1]);
n-=2;
}
//less than 4
if(3==n)for(int i=0;i<3;++i)ans+=a[i] ;
else if(2==n)ans+=a[2];
else if(1==n)ans+=a[1];
return ans;
}
};
55. 跳跃游戏
难度中等1259
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 1040 <= nums[i] <= 105
题解
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
int rightmost = 0;
for (int i = 0; i < n; ++i) {
if (i <= rightmost) {
rightmost = max(rightmost, i + nums[i]);
if (rightmost >= n - 1) {
return true;
}
}
}
return false;
}
};
45. 跳跃游戏 II
难度中等1051
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 10000 <= nums[i] <= 105
题解
class Solution {
public:
int jump(vector<int>& nums) {
if(nums.size()==1)return 0;
int n=nums.size(),count =0;
int step=0,end=0;
int k = 0;
for(int i=0;i<n;i++){
k=max(k,i+nums[i]);
if(k>=nums.size()-1)return step+1;
if(end==i){
step++;
end=k;
}
}
return step;
}
};
//dfs 和 bfs
class Solution {
public:
vector<int> minSteps;
void dfs(vector<int>& nums, int cur) {
for (int next = cur + 1; next < nums.size() && next <= cur + nums[cur]; next++) {
if (minSteps[next] <= minSteps[cur] + 1) continue; // 剪枝。当前的方案比已有的方案还差,就不要递归了
minSteps[next] = minSteps[cur] + 1;
dfs(nums, next); // 递归尝试所有跳数
}
}
void bfs(vector<int>& nums, int cur) {//index
queue<int>q;
q.push(cur);
int temp;
while(!q.empty()){
temp=q.front(),q.pop();
for(int i=temp+1;i<nums.size()&& i<=temp+nums[temp];++i){
if(minSteps[i]<=minSteps[temp]+1) continue;
minSteps[i]=minSteps[temp]+1;
q.push(i) ;
}
}
}
int jump(vector<int>& nums) {
if(nums.size()==1)return 0;
int n=nums.size();
minSteps=vector<int>(n,INT_MAX);
minSteps[0]=0;
bfs(nums,0);
//queue<pair<int,int>>q;
// q.push({0,0})
return minSteps[n-1];
}
};
455. 分发饼干
难度简单350
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
题解
因为饥饿度最小的孩子最容易吃饱,所以我们先考虑这个孩子。为了尽量使得剩下的饼干可以满足饥饿度更大的孩子,所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {//g:孩子 s:饼干
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int child=0,cookie=0;
while(child<g.size() && cookie<s.size()){
if(g[child]<=s[cookie]) child++;
++cookie;
}
return child;
}
};
135. 分发糖果
难度困难590
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入:[1,0,2]
输出:5
解释:你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:[1,2,2]
输出:4
解释:你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
题解
把所有孩子的糖果数初始化为 1;先从左往右遍历一遍,如果右边孩子的评分比左边的高,则右边孩子的糖果数更新为左边孩子的糖果数加 1;再从右往左遍历一遍,如果左边孩子的评分比右边的高,且左边孩子当前的糖果数不大于右边孩子的糖果数,则左边孩子的糖果数更新为右边孩子的糖果数加 1。
class Solution {
public:
int candy(vector<int>& ratings) {
int size = ratings.size();
if (size < 2) {
return size;
}
vector<int> num(size, 1);
for (int i = 1; i < size; ++i) {
if (ratings[i] > ratings[i-1]) {
num[i] = num[i-1] + 1;
}
}
for (int i = size - 1; i > 0; --i) {
if (ratings[i] < ratings[i-1]) {
num[i-1] = max(num[i-1], num[i] + 1);
}
}
return accumulate(num.begin(), num.end(), 0);
}
};
738. 单调递增的数字
难度中等189
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
(当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。)
示例 1:
输入: N = 10
输出: 9
示例 2:
输入: N = 1234
输出: 1234
示例 3:
输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。
题解
class Solution {
public:
int monotoneIncreasingDigits(int n) {
string temp=to_string(n);
int flag;
for(int i=temp.size()-1;i>0;--i){
if(temp[i-1]>temp[i]){
flag=i;
temp[i-1]--;
}
}
for(int i=flag;i<temp.size();++i){
temp[i]='9' ;
}
return stoi(temp);
}
};
435. 无重叠区间
难度中等452
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
- 可以认为区间的终点总是大于它的起点。
- 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
题解
选择的区间结尾越小,余留给其它区间的空间就越大,就越能保留更多的区间。因此,我们采取的贪心策略为,优先保留结尾小且不相交的区间。
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size()<2) return 0;
sort(intervals.begin(),intervals.end(),[&](const vector<int>&a,const vector<int>&b){
return (a[1]<b[1]);
});
int ans=0,pre=intervals[0][1];
for(int i=1;i<intervals.size();++i)
{
if(intervals[i][0]<pre)ans++;
else pre = intervals[i][1];
}
return ans;
}
};
56. 合并区间
难度中等1016
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
题解
class Solution{
vector
};
452. 用最少数量的箭引爆气球
难度中等431
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 x``start,x``end, 且满足 xstart ≤ x ≤ x``end,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]]
输出:2
示例 4:
输入:points = [[1,2]]
输出:1
示例 5:
输入:points = [[2,3],[2,3]]
输出:1
提示:
1 <= points.length <= 104points[i].length == 2-231 <= xstart < xend <= 231 - 1
题解
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(),points.end(),[&](const vector<int>&a, const vector<int>&b){
return (a[1]<b[1]);
});
int ans=1;
int max=points[0][1];//最远能射的距离
for(int i=1;i<points.size();++i){
if(max >= points[i][0]) continue;
else { ans++; max=points[i][1];} //换最远的距离
}
return ans;
}
};
763. 划分字母区间
难度中等526收藏分享切换为英文接收动态反馈
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
输入:S = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca", "defegde", "hijhklij"。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
S的长度在[1, 500]之间。S只包含小写字母'a'到'z'。
题解
class Solution {
public:
vector<int> partitionLabels(string s) {
int a[26]={0};
for(int i=0;i<s.size();++i){//记录元素最后出现位置
a[s[i]-'a']=i;
}
int start=0,end=0;
vector<int>ans;
for(int i=0;i<s.size();++i){
end = max(end,a[s[i]-'a']); // 找到字符出现的最远边界
if(i == end){ //到达边界,换起始位置
ans.emplace_back(end-start+1);
start=i+1;
}
}
return ans;
}
};
605. 种花问题
难度简单365
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。
示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1
输出:true
示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2
输出:false
提示:
1 <= flowerbed.length <= 2 * 104flowerbed[i]为0或1flowerbed中不存在相邻的两朵花0 <= n <= flowerbed.length
题解
class Solution {
public:
bool canPlaceFlowers(vector<int>& a, int n) {
for(int i=0;i<a.size();i++){
//判断当前位置能否种花
//能种 ❀ 的情况
if( a[i]==0 \
&& (i == a.size()-1 ||a[i+1] == 0) \
&& (i==0 || a[i-1]==0) ){a[i]=1;n--;}
}
return n<=0;
}
};
LCP 33. 蓄水
难度简单27
给定 N 个无限容量且初始均空的水缸,每个水缸配有一个水桶用来打水,第 i 个水缸配备的水桶容量记作 bucket[i]。小扣有以下两种操作:
- 升级水桶:选择任意一个水桶,使其容量增加为
bucket[i]+1 - 蓄水:将全部水桶接满水,倒入各自对应的水缸
每个水缸对应最低蓄水量记作 vat[i],返回小扣至少需要多少次操作可以完成所有水缸蓄水要求。
注意:实际蓄水量 达到或超过 最低蓄水量,即完成蓄水要求。
示例 1:
输入:
bucket = [1,3], vat = [6,8]输出:
4解释:
第 1 次操作升级 bucket[0];
第 2 ~ 4 次操作均选择蓄水,即可完成蓄水要求。
示例 2:
输入:
bucket = [9,0,1], vat = [0,2,2]输出:
3解释:
第 1 次操作均选择升级 bucket[1]
第 2~3 次操作选择蓄水,即可完成蓄水要求。
提示:
1 <= bucket.length == vat.length <= 1000 <= bucket[i], vat[i] <= 10^4
题解
class Solution {
public:
int storeWater(vector<int>& bucket, vector<int>& vat) {
int n = bucket.size();
int maxk = *max_element(vat.begin(), vat.end());
if (!maxk) {
return 0;
}
int cur; //升级杯子次数
int ans = INT_MAX;
for (int k = 1; k <= maxk; ++k) { //枚举倒水次数,最多需要maxk次能装满
cur = k; //倒水次数k
for (int i = 0; i < n; ++i) {
int least = vat[i] / k + (vat[i] % k != 0); //当倒水次数为k时,最少需要least大小的杯子
cur += max(least - bucket[i], 0); //需要升级杯子的次数 + 倒水次数
}
ans = min(ans, cur);
}
return ans;
}
};
918. 环形子数组的最大和
难度中等174
给定一个由整数数组 A 表示的环形数组 C,求 **C** 的非空子数组的最大可能和。
在此处,环形数组意味着数组的末端将会与开头相连呈环状。(形式上,当0 <= i < A.length 时 C[i] = A[i],且当 i >= 0 时 C[i+A.length] = C[i])
此外,子数组最多只能包含固定缓冲区 A 中的每个元素一次。(形式上,对于子数组 C[i], C[i+1], ..., C[j],不存在 i <= k1, k2 <= j 其中 k1 % A.length = k2 % A.length)
示例 1:
输入:[1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:[5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:[3,-1,2,-1]
输出:4
解释:从子数组 [2,-1,3] 得到最大和 2 + (-1) + 3 = 4
示例 4:
输入:[3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
示例 5:
输入:[-2,-3,-1]
输出:-1
解释:从子数组 [-1] 得到最大和 -1
提示:
-30000 <= A[i] <= 300001 <= A.length <= 30000
题解
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
int maxCur, maxSum, minCur, minSum, total;
maxCur = maxSum = minCur = minSum = total = nums[0];
for(int i = 1; i < nums.size(); ++i) {
maxCur = max(maxCur,0)+nums[i];
maxSum = max(maxSum, maxCur);
minCur = min(minCur,0) + nums[i];
minSum = min(minSum, minCur);
total += nums[i];
}
if(maxSum < 0)
return maxSum;
return max(maxSum, total - minSum);
}
};
402. 移掉 K 位数字
难度中等620
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
示例 1 :
输入:num = "1432219", k = 3
输出:"1219"
解释:移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。
示例 2 :
输入:num = "10200", k = 1
输出:"200"
解释:移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入:num = "10", k = 2
输出:"0"
解释:从原数字移除所有的数字,剩余为空就是 0 。
提示:
1 <= k <= num.length <= 105num仅由若干位数字(0 - 9)组成- 除了 0 本身之外,
num不含任何前导零
题解
class Solution {
public:
string removeKdigits(string num, int k) {
while (k--) {
int n = num.size(), i = 0;
while (i + 1 < n && num[i] <= num[i + 1]) ++i;//每次剔除向右大的
num.erase(i, 1); // 每次 erase 的时间复杂度为O(n)
}
auto i = num.find_first_not_of("0");
return i == string::npos ? "0" : num.substr(i);
}
};
◉ 十一、二叉树
class TreeNode {
public:
int val;
TreeNode *left;
TreeNode *right;
TreeNode(const int& x):val(x),left(nullptr),right(nullptr){}
};
//销毁二叉树
void deleteTree(TreeNode* root) {
if (root == nullptr)return;
else if (root) {
deleteTree(root->left);
deleteTree(root->right);
delete root;
root = nullptr;
}
}
▼二叉树的遍历
//前序
vector<int> preorderTraversal(TreeNode* root) { //入栈顺序为:根->右->左
vector<int> res;
if(root == NULL)
return res;
stack<TreeNode *> st;
st.push(root);
while(!st.empty())
{
TreeNode *temp = st.top();
st.pop();
res.emplace_back(temp->val); //visit
if(temp->right)
st.push(temp->right); //右
if(temp->left)
st.push(temp->left); //左
}
return res;
}
//前序dfs
void preorder(TreeNode *root, vector<int> &res) {
if (root == nullptr) {
return ;
}
res.emplace_back(root->val);
preorder(root->left, res);
preorder(root->right, res);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
preorder(root, res);
return res;
}
//中序dfs
void preorder(TreeNode *root, vector<int> &res) {
if (root == nullptr) {
return ;
}
preorder(root->left, res);
res.emplace_back(root->val);
preorder(root->right, res);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
preorder(root, res);
return res;
}
//中序
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while (root != nullptr || !stk.empty()) {//注意是 或
while (root != nullptr) { //入栈至最左节点
stk.push(root);
root = root->left;
}
root = stk.top(); //出栈访问
stk.pop();
res.push_back(root->val);
root = root->right; //转至右节点
}
return res;
}
//后序dfs
void dfs(TreeNode*root ,vector<int>&ans){
if(root==nullptr)return;
dfs(root->left,ans);
dfs(root->right,ans);
ans.emplace_back(root->val);
return;
}
vector<int> postorderTraversal(TreeNode* root) {
if(root==nullptr)return{};
vector<int> ans;
it(root,ans);
return ans;
}
//后序
vector<int> postorderTraversal(TreeNode* root) { //入栈顺序为:根->左->右
if(root==nullptr)return{};
vector<int> ans;
stack<TreeNode*>s;
TreeNode* p=root;
s.push(p);
while(!s.empty()){
p=s.top();s.pop();
ans.emplace_back(p->val); //访问根节点
if(p->left)s.push(p->left); //左
if(p->right)s.push(p->right); //右
}
reverse(ans.begin(),ans.end()); //反转
return ans;
}
// 层序
vector<vector<int>> levelOrder(TreeNode* root) {
vector <vector <int>> ret;
if (!root) {
return ret;
}
queue <TreeNode*> q;
q.push(root);
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector <int> ());
for (int i = 1; i <= currentLevelSize; ++i) { //入队顺序为:根->左->右
auto node = q.front(); q.pop();
ret.back().push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
//层序
class Solution {
public:
vector<vector<int>>ans;
void dfs(TreeNode*root,int depth){
if(!root)return;
if(depth>=ans.size()) ans.emplace_back(vector<int>());
ans[depth].emplace_back(root->val);
dfs(root->left,depth+1);
dfs(root->right,depth+1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
if(root==nullptr)return {};
dfs(root, 0);
return ans;
}
};
思考
n个节点的二叉树或二叉搜索树有多少种形态!
答:符合卡特兰数,即
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LMnbdprs-1630453061508)(C:\Users\bj\AppData\Roaming\Typora\typora-user-images\image-20210703083859289.png)]
剑指 Offer 68 - II. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
题解
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr) return root;
if(root==p||root==q) return root; //如果根节点就是p或者q,返回根节点
//分别去左右子树里面找
TreeNode* l=lowestCommonAncestor(root->left,p,q);
TreeNode* r=lowestCommonAncestor(root->right,p,q);
if(l&&r) return root;//p,q各在一边,说明当前的根就是最近共同祖先
else if(l)return l;//说明p,q都在左子树
else if(r)return r;//说明p,q都在右子树
return nullptr;
}
//或
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || root == p || root == q) return root; //注意看条件
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(!left) return right;
if(!right) return left;
return root;
}
剑指 Offer 36. 二叉搜索树与双向链表
难度中等281
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
题解
class Solution {
public:
void biuld(Node* root,Node* &head,Node* &tail){
if(!root) return ;
biuld(root->left,head,tail);
if(!head) head = tail = root;
else{
tail->right = root;
root->left = tail;
tail = root;
}
biuld(root->right,head,tail);
}
Node* treeToDoublyList(Node* root) {
if (!root) return nullptr;
Node* head = nullptr,*tail = nullptr;
biuld(root,head,tail);
tail->right = head;
head->left = tail;
return head;
}
};
剑指 Offer 07. 重建二叉树
难度:中等
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
限制:
0 <= 节点个数 <= 5000
题解
class Solution {
public:
unordered_map<int,int>index;
TreeNode*build_tree(vector<int>& preorder, vector<int>& inorder,int s1,int e1,int s2,int e2){
TreeNode *root=new TreeNode;
root->val=preorder[s1];
int i=index[root->val];
//for( i=s2;inorder[i]!=root->val;i++);
int llen=i-s2;
int rlen=e2-i;
if(llen){
root->left=build_tree(preorder,inorder,s1+1,s1+llen,s2,s2+llen-1);
}
else{
root->left=nullptr;
}
if(rlen){
root->right=build_tree(preorder,inorder,e1-rlen+1,e1,e2-rlen+1,e2);
}
else root->right=nullptr;
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n=preorder.size();
if(n==0)return nullptr;
for(int i=0;i<n;i++){
index[inorder[i]]=i; //确定每棵子树的根节点
}
return build_tree(preorder,inorder,0,n-1,0,n-1);
}
};
判断是否是完全二叉树
题解
bool isComplete(TreeNode* root){
queue<TreeNode*> a;
TreeNode *temp = root;
a.push(temp);
while(!a.empty()){
temp=q.front() ; q.pop();
if(temp){
a.push(temp->left);
a.push(temp->right);
}
else{
while(!a.empty()){
temp=q.front() ; q.pop();
if(temp)return false;
}
}
}
return true;
}
剑指 Offer 28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 / \ 2 2 / \ / \ 3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
\
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
限制:
0 <= 节点个数 <= 1000
题解
class Solution {
public:
bool helper(TreeNode* l,TreeNode *r){
if(l==nullptr&& r==nullptr)return true;
if(l==nullptr||r==nullptr||l->val!=r->val)return false;
return helper(l->right,r->left)&&helper(l->left,r->right);
}
bool isSymmetric(TreeNode* root) {
if(root==nullptr||(root->left==nullptr&&root->right==nullptr))return true;
return helper(root->left,root->right);
}
};
//迭代
class Solution {
public:
bool bthelp(TreeNode*l,TreeNode*r){
queue<TreeNode*>q;
q.push(l);
q.push(r);
while(!q.empty()){
l=q.front();q.pop();
r=q.front();q.pop();
if(l==nullptr && r==nullptr)continue;
if(l==nullptr||r==nullptr||l->val!=r->val)return false;
q.push(l->left);
q.push(r->right);
q.push(l->right);
q.push(r->left);
}
return true;
}
bool isSymmetric(TreeNode* root) {
if(root==nullptr)return true;
return bthelp(root->left,root->right);
}
};
剑指 Offer 27. 二叉树的镜像
难度简单143收藏分享切换为英文接收动态反馈
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/
2 7
/ \ /
1 3 6 9
镜像输出:
4
/
7 2
/ \ /
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
限制:
0 <= 节点个数 <= 1000
题解
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(!root)return root;
TreeNode* t=root->left;
root->left=root->right;
root->right=t;
mirrorTree(root->left);
mirrorTree(root->right);
return root;
}
};
//迭代
class Solution {
public:
stack<TreeNode*>s;
TreeNode* mirrorTree(TreeNode* root) {
if(!root)return root;
TreeNode* t=root;
s.push(t);
while(!s.empty()){
t=s.top();s.pop();
swap(t->left,t->right);
if(t->right)s.push(t->right);
if(t->left)s.push(t->left);
}
return root;
}
};
剑指 Offer 26. 树的子结构
难度中等303
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3 / \ 4 5 / \ 1 2
给定的树 B:
4 / 1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000
题解
class Solution {
public:
bool helper(TreeNode* A, TreeNode* B){
if(A==NULL||B==NULL)
return B==NULL?true:false;
return (A->val==B->val)&&helper(A->left,B->left)&&helper(A->right,B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if(A==NULL||B==NULL)
return false;
return helper(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B);
}
};
剑指 Offer 55 - I. 二叉树的深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
//迭代
class Solution {
private:
queue<TreeNode*> q;
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)return 0;
int n=0; //深度从0开始统计
q.push(root);
while(!q.empty()){
int size=q.size();
for(int i=0;i<size;++i){
TreeNode* temp = q.front();
q.pop();
if(temp->left)q.push(temp->left);
if(temp->right)q.push(temp->right);
}
n++;
}
return n;
}
};
//递归
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
面试题 04.04. 检查平衡性
难度简单61收藏分享切换为英文接收动态反馈
实现一个函数,检查二叉树是否平衡。在这个问题中,平衡树的定义如下:任意一个节点,其两棵子树的高度差不超过 1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
题解
自底向上的方法可以有效减少重复访问
//后序遍历
class Solution {
public:
bool f=true;
int depth(TreeNode*root){
if(!root)return 0;
int ldepth=depth(root->left);
int rdepth=depth(root->right);
if(abs(ldepth-rdepth)>1) f=false;
return max(ldepth,rdepth)+1;
}
bool isBalanced(TreeNode* root) {
if(!root) return true;
depth(root);
return f;
}
};
543. 二叉树的直径
难度简单731收藏分享切换为英文接收动态反馈
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
题解
class Solution {
public:
int ans=0;
int depth(TreeNode* root){
if(!root)return 0;
int l=depth(root->left),r=depth(root->right);
ans = max(ans,l+r);
return max(l,r)+1;
}
int diameterOfBinaryTree(TreeNode* root) {
depth(root);
return ans;
}
};
124. 二叉树中的最大路径和
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
题解
class Solution {
public:
int ans=INT_MIN;
int fun(TreeNode* root) {
if(root==nullptr){
return 0;
}
// 如果子树路径和为负则应当置0表示最大路径不包含子树
int left=max(0,fun(root->left));
int right=max(0,fun(root->right));
// 判断在该节点包含左右子树的路径和是否大于当前最大路径和
ans=max(ans,left+right+root->val);
// 选择左子树/右子树+当前节点
return max(left,right)+root->val;
}
int maxPathSum(TreeNode* root) {
fun(root);
return ans;
}
};
687. 最长同值路径
难度中等473
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出:
2
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出:
2
注意: 给定的二叉树不超过10000个结点。 树的高度不超过1000。
题解
class Solution {
public:
int ans=0;
int dfs(TreeNode*root){
if(!root)return 0;
const int l=dfs(root->left),r=dfs(root->right);
const int lp=(root->left&&root->left->val==root->val)?l:0;
const int rp=(root->right&&root->right->val==root->val)?r:0;
ans=max(ans,lp+rp);
return max(lp,rp)+1;
}
int longestUnivaluePath(TreeNode* root) {
dfs(root);
return ans;
}
};
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
题解
//迭代
class Solution {
private:
queue<TreeNode*>a;
public:
int minDepth(TreeNode* root) {
if(!root)return 0;
TreeNode * t=root;
a.push(t);
int n=1; //深度从1开始统计
while(!a.empty()){
int size=a.size();
for(int i=0;i<size;++i){
t=a.front();a.pop();
if(!t->left&&!t->right)return n;
if(t->left)a.push(t->left);
if(t->right)a.push(t->right);
}
n++;
}
return 0;
}
};
//递归
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root)return 0;
int l = minDepth(root->left),r = minDepth(root->right);
return (l&&r)?1+min(l,r):1+l+r;
}
};
993. 二叉树的堂兄弟节点
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
示例 2:
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
示例 3:
输入:root = [1,2,3,null,4], x = 2, y = 3
输出:false
提示:
- 二叉树的节点数介于
2到100之间。 - 每个节点的值都是唯一的、范围为
1到100的整数。
题解
//DFS
class Solution {
public:
TreeNode* p1=NULL; //father1: x
TreeNode* p2=NULL; //father2: y
int h1=-1,h2=-1;
void dfs(TreeNode* root,int x,int y,int h){
if(!root) return;
if(root->left&&root->left->val==x){ //father1: x
p1=root;h1=h;
}
if(root->right&&root->right->val==x){ //father1: x
p1=root;h1=h;
}
if(root->left&&root->left->val==y){ //father2: y
p2=root;h2=h;
}
if(root->right&&root->right->val==y){ //father2: y
p2=root;h2=h;
}
dfs(root->left,x,y,h+1);
dfs(root->right,x,y,h+1);
}
bool isCousins(TreeNode* root, int x, int y) {
dfs(root,x,y,0);
return (h1==h2)&&(p1!=p2); //同层不同父
}
};
//BFS
class Solution {
private:
queue<TreeNode*> a;
public:
bool isCousins(TreeNode* root, int x, int y) {
if(!root)return false;
TreeNode* t=root;
a.push(root);
while(!a.empty()){
int size= a.size();
int f=0;
for(int i=0;i<size;++i){
t = a.front();a.pop();
if(t->val==x||t->val==y)++f;
if(t->left&& t->right){//排除亲兄弟
if((t->left->val==x&&t->right->val==y )||(t->left->val==y&&t->right->val==x))return false;
}
if(t->left)a.push(t->left);
if(t->right)a.push(t->right);
}
if(f==2)return true; //在同一层
}
return false;
}
};
二叉树节点的所有祖先节点
在二叉树中查找值为x的节点,找出该节点的所有祖先节点,假设x节点只有一个。
题解
bool PrintAncestors1(TreeNode *T, const int& x, vector<int>&ans) {
if (!T)
return false;
if (T->val == x) {
return true;
}
//如果一颗二叉树他的左孩子有要查询的结点或者他的右孩子里面有要查询的结点那么该节点就是祖先结点
if (PrintAncestors1(T->left, x,ans) || PrintAncestors1(T->right, x,ans)) {
ans.emplace_back(T->val);
return true;
}
else {
return false;
}
}
662. 二叉树最大宽度
给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与**满二叉树(full binary tree)**结构相同,但一些节点为空。
每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
示例 1:
输入:
1
/ \
3 2
/ \ \
5 3 9
输出: 4
解释: 最大值出现在树的第 3 层,宽度为 4 (5,3,null,9)。
示例 2:
输入:
1
/
3
/ \
5 3
输出: 2
解释: 最大值出现在树的第 3 层,宽度为 2 (5,3)。
示例 3:
输入:
1
/ \
3 2
/
5
输出: 2
解释: 最大值出现在树的第 2 层,宽度为 2 (3,2)。
示例 4:
输入:
1
/ \
3 2
/ \
5 9
/ \
6 7
输出: 8
解释: 最大值出现在树的第 4 层,宽度为 8 (6,null,null,null,null,null,null,7)。
注意: 答案在32位有符号整数的表示范围内。
题解
记忆化搜索,每一层的记忆元素如下
1
/ \
0 1
/ \ / \
0 1 2 3
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if(root == NULL) return 0;
queue<pair<TreeNode*, int>> q; //pair的第二个位置记录当前是第几个节点
q.push({root, 1});
int width = 0;
while(!q.empty())
{
int count = q.size();
int start = q.front().second, index; //start是本层起点, index是本层当前遍历到的节点的索引
while(count--)
{
TreeNode *tmp = q.front().first;
index = q.front().second;
q.pop();
if(tmp->left) q.push({tmp->left , index * 2 - start * 2}); //存偏移量,防止索引位置太大溢出
if(tmp->right) q.push({tmp->right, index * 2 + 1 - start * 2});
}
width = max(width, index - start + 1);
}
return width;
}
};
257. 二叉树的所有路径
难度简单526
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
题解
class Solution{
public:
vector<string> ans;
void binaryTreePaths(TreeNode * root, string path) {
path+= to_string(root->val);
if(!root->left&&!root->right){
ans.emplace_back(path);
return ;
}
if(root->left) binaryTreePaths(root->left, path+"->");
if(root->right) binaryTreePaths(root->right, path+"->");
}
vector<string> binaryTreePaths(TreeNode* root) {
if(!root)return{};
binaryTreePaths(root,"") ;
return ans;
}
};
112. 路径总和
难度简单611
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
示例 3:
输入:root = [1,2], targetSum = 0
输出:false
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
题解
class Solution {
public:
int sum=0;
bool ans;
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root)return false;
sum+=root->val;//选择
if(sum==targetSum&&!root->left&&!root->right)return true;
if(root->left) ans = hasPathSum(root->left,targetSum);
if(root->right)ans= hasPathSum(root->right,targetSum);
sum-=root->val;//取消
return ans;
}
};
113. 路径总和 II
难度中等520
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
题解
class Solution {
public:
vector<vector<int>>ans;
vector<int>path;
int sum=0;
void dfs(TreeNode*root,int t){
if(!root)return ;
sum+=root->val;
path.emplace_back(root->val);
if(sum==t&&!root->left&&!root->right){
ans.emplace_back(path); //return;加上此句表示找到就返回,不继续寻找
}
if(root->left) dfs(root->left,t);
if(root->right) dfs(root->right,t);
sum-=root->val;
path.pop_back();
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(!root)return {};
dfs(root,targetSum);
return ans;
}
};
437. 路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
题解
class Solution {
public:
unordered_map<int, int> count;// k:前缀和 v:方法数
int pathSum(TreeNode* root, int sum) {
count[0] = 1;
return helper(root, sum, 0);
}
int helper(TreeNode* root, int sum, int prefix_sum) {
if (!root) return 0;
int res = 0;//方法数
prefix_sum += root->val;//当前和
res += count[prefix_sum - sum];
count[prefix_sum]++;
res += helper(root->left, sum, prefix_sum) + helper(root->right, sum, prefix_sum);
count[prefix_sum]--;
return res;
}
};
129. 求根节点到叶节点数字之和
难度中等375收藏分享切换为英文接收动态反馈
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
题解
class Solution {
public:
int helper(TreeNode* root, int sum){
if(!root)
return 0;
else if (!root->left && !root->right)
return 10*sum + root->val;
return helper(root->left, 10*sum + root->val) +
helper(root->right, 10*sum + root->val);
}
int sumNumbers(TreeNode* root) {
return helper(root, 0);
}
};
114. 二叉树展开为链表
难度:中等
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
题解
class Solution {
public:
TreeNode* after = nullptr;
void flatten(TreeNode* root) {
if(!root)return;
flatten(root->right);
flatten(root->left);
root->right=after;
root->left=nullptr;
after=root;
}
};
//time: O(n) space:O(1)
class Solution {
public:
void flatten(TreeNode* root) {
if(!root||(!root->left&&!root->right))return ;
TreeNode*cur=root;
while(cur){
if(cur->left){
//record the next node, it is equal to the cur->right
TreeNode* next = cur->left;
TreeNode* temp = next; //find the rightmost node of next
while(temp->right){
temp=temp->right;
}
//the next node of the rightmost node of next is cur->right
temp->right = cur->right;
cur->left = nullptr; //set the left node to nullptr
cur->right = next;
}
cur=cur->right; //move the pointer
}
return ;
}
面试题 17.12. BiNode
难度:简单
二叉树数据结构TreeNode可用来表示单向链表(其中left置空,right为下一个链表节点)。实现一个方法,把二叉搜索树转换为单向链表,要求依然符合二叉搜索树的性质,转换操作应是原址的,也就是在原始的二叉搜索树上直接修改。
返回转换后的单向链表的头节点。
**注意:**本题相对原题稍作改动
示例:
输入: [4,2,5,1,3,null,6,0]
输出: [0,null,1,null,2,null,3,null,4,null,5,null,6]
提示:
- 节点数量不会超过 100000。
题解
class Solution {
public:
TreeNode* res=new TreeNode(-1);
TreeNode* tmp=res;
TreeNode* convertBiNode(TreeNode* root) {
if(!root)return root;
convertBiNode(root->left);
tmp->right=root;
root->left=nullptr;
tmp=tmp->right;
convertBiNode(root->right);
return res->right;
}
};
617. 合并二叉树
难度简单714
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。
题解
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(!t1)
return t2;
if(!t2)
return t1;
TreeNode *root=new TreeNode(0);
if(t1)
root->val+=t1->val;
if(t2)
root->val+=t2->val;
root->left=mergeTrees(t1?t1->left:nullptr,t2?t2->left:nullptr);
root->right=mergeTrees(t1?t1->right:nullptr,t2?t2->right:nullptr);
return root;
}
};
116. 填充每个节点的下一个右侧节点指针
难度中等480
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
提示:
- 树中节点的数量少于
4096 -1000 <= node.val <= 1000
题解
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr || root->left == nullptr)
return root;
root->left->next = root->right;
if (root->next) //例如节点5->6
root->right->next = root->next->left;
connect(root->left);
connect(root->right);
return root;
}
};
//通用BFS!!!
class Solution {
public:
Node* connect(Node* root) {
if (!root) return root;
Node* cur = root;
while (cur) {
Node* head = new Node(), *tail = head;
for (Node* p = cur; p; p = p->next) {
if (p->left) tail = tail->next = p->left;//{ tail->next = p->left;tail = tail->next;}
if (p->right) tail = tail->next = p->right;
}
cur = head->next;
}
return root;
}
};
LCP 34. 二叉树染色
难度中等21
小扣有一个根结点为 root 的二叉树模型,初始所有结点均为白色,可以用蓝色染料给模型结点染色,模型的每个结点有一个 val 价值。小扣出于美观考虑,希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个,求所有染成蓝色的结点价值总和最大是多少?
示例 1:
输入:
root = [5,2,3,4], k = 2输出:
12解释:
结点 5、3、4 染成蓝色,获得最大的价值 5+3+4=12
示例 2:
输入:
root = [4,1,3,9,null,null,2], k = 2输出:
16解释:结点 4、3、9 染成蓝色,获得最大的价值 4+3+9=16
提示:
1 <= k <= 101 <= val <= 100001 <= 结点数量 <= 10000
题解
class Solution {
public:
array<int, 11> dfs(TreeNode* root, int k) {
array<int, 11> f = {0};
if (!root) return f;
array<int, 11> l = dfs(root->left, k);
array<int, 11> r = dfs(root->right, k);
f[0] = *max_element(l.begin(), l.end()) + *max_element(r.begin(), r.end());
for (int i = 1; i <= k; ++i) {
for (int j = 0; j < i; ++j) {
f[i] = max(f[i], root->val + l[j] + r[i - j - 1]);
}
}
return f;
}
public:
int maxValue(TreeNode* root, int k) {
array<int, 11> f = dfs(root, k);
return *max_element(f.begin(), f.end());
}
};
199. 二叉树的右视图
难度中等487
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
题解
//dfs
class Solution {
public:
vector<int> ans;
void dfs(TreeNode* root,int depth){
if(!root)return ;
if(ans.size()==depth)ans.emplace_back(root->val);
depth++;
dfs(root->right,depth);
dfs(root->left,depth);
}
vector<int> rightSideView(TreeNode* root) {
if(!root) return {};
dfs(root,0);
return ans;
}
};
//bfs
class Solution {
public:
queue<TreeNode*>q;
vector<int> ans;
vector<int> rightSideView(TreeNode* root) {
if(!root) return {};
q.push(root);
TreeNode* t=root;
while(!q.empty()){
int size=q.size();
for(int i=0;i<size;++i){
t = q.front();q.pop();
if(i==size-1) ans.emplace_back(t->val);
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
}
return ans;
}
};
//第二次写
class Solution {
public:
vector<int> ans;
void bfs(TreeNode* root){
queue<TreeNode*>q;
q.push(root);
TreeNode* temp = nullptr;
while(!q.empty()){
ans.emplace_back(q.front()->val); //每一层第一个元素
for(int i=q.size()-1;i>=0;--i){
temp =q.front(),q.pop();
if(temp->right)q.push(temp->right);
if(temp->left)q.push(temp->left);
}
}
}
vector<int> rightSideView(TreeNode* root) {
if(!root) return {};
bfs(root);
return ans;
}
};
▼二叉搜索树
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
题解
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr) return nullptr;
if(root->val > p->val&&root->val > q->val){//说明p,q都在左子树
return lowestCommonAncestor(root->left,p,q);}
else if(root->val < p->val && root->val < q->val)//说明p,q都在右子树
return lowestCommonAncestor(root->right,p,q);
return root;//p,q各在一边,说明当前的根就是最近共同祖先
}
96. 不同的二叉搜索树
难度中等1213收藏分享切换为英文接收动态反馈
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
题解
class Solution { //cantalan数
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
700. 二叉搜索树中的搜索
难度简单138收藏分享切换为英文接收动态反馈
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和值: 2
你应该返回如下子树:
2
/ \
1 3
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
题解
//迭代
class Solution {
public:
TreeNode* searchBST(TreeNode* root, const int& val) {
while(root&&val!=root->val){
if(val<root->val)root=root->left;
else root=root->right;
}
return root;
}
};
//递归
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (root == nullptr || root->val == val)//相等
{
return root;
}
else if (root->val < val) //小于
{
return searchBST(root->right, val);
}
else
{
return searchBST(root->left, val);
}
}
};
面试题 04.06. 后继者
难度中等67收藏分享切换为英文接收动态反馈
设计一个算法,找出二叉搜索树中指定节点的“下一个”节点(也即中序后继)。
如果指定节点没有对应的“下一个”节点,则返回null。
示例 1:
输入: root = [2,1,3], p = 1
2
/ \
1 3
输出: 2
示例 2:
输入: root = [5,3,6,2,4,null,null,1], p = 6
5
/ \
3 6
/ \
2 4
/
1
输出: null
题解
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
TreeNode* res = nullptr;
while(root) {
if(root->val > p->val) { //找到刚好大于p的节点
res = root;
root = root->left;
}
else root = root->right;
}
return res;
}
};
701. 二叉搜索树中的插入操作
难度中等191
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 给定的树上的节点数介于
0和10^4之间 - 每个节点都有一个唯一整数值,取值范围从
0到10^8 -10^8 <= val <= 10^8- 新值和原始二叉搜索树中的任意节点值都不同
题解
//递归
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root){
return root=new TreeNode(val);
}
else if(root->val>val) root->left=insertIntoBST(root->left,val);
else root->right=insertIntoBST(root->right,val);
return root;
}
};
//迭代
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int k) {
if(!root){
return root=new TreeNode(k);
}
TreeNode*parent=root,*p=root;
while(p){
parent=p;
p=p->val < k?p->right:p->left;
}
if(parent->val < k)parent->right = new TreeNode(k);
else parent->left = new TreeNode(k);
return root;
}
};
108. 将有序数组转换为二叉搜索树
难度简单791
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
题解
class Solution {
public:
TreeNode* helper(vector<int>& nums,int l,int r){
if(r<l)return nullptr;
int m=l+((r-l)>>1);
TreeNode* root =new TreeNode(nums[m]);
root->left=helper(nums,l,m-1);
root->right=helper(nums,m+1,r);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
if(nums.size()==0)return nullptr;
return helper(nums,0,nums.size()-1);
}
};
109. 有序链表转换二叉搜索树
难度中等548
给定一个单链表,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定的有序链表: [-10, -3, 0, 5, 9],
一个可能的答案是:[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
题解
class Solution{
public:
ListNode* h;
TreeNode* dfs(int s,int e){ //中序遍建立树
if(s>e)return nullptr;
int m=(s+e+1)>>1;
TreeNode* root=new TreeNode();
root->left=dfs(s,m-1);
root->val=h->val;
h=h->next;
root->right = dfs(m+1,e);
return root;
}
TreeNode* sortedListToBST(ListNode* head) {
if(!head)return nullptr;
if(!head->next)return new TreeNode(head->val);
h=head;
ListNode *temp=head; int n=0;
while(temp){ //统计链表节点数
n++;
temp=temp->next;
}
return dfs(0,n-1);
}
};
//方法二:前序遍历
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
return buildtree(head, nullptr);
}
ListNode* getmid(ListNode* left, ListNode* right) {//找中
ListNode* slow = left;
ListNode* fast = left;
while (fast != right && fast->next != right) {
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
TreeNode* buildtree(ListNode* left, ListNode* right) {
if (left == right)
return nullptr;
ListNode* mid = getmid(left, right);
TreeNode* root = new TreeNode(mid->val);
root->left = buildtree(left, mid);
root->right = buildtree(mid->next, right);
return root;
}
};
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
说明: 要求算法时间复杂度为 O(h),h 为树的高度。
示例:
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
5
/ \
4 6
/ \
2 7
另一个正确答案是 [5,2,6,null,4,null,7]。
5
/ \
2 6
\ \
4 7
题解
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key)
{
if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了
if (root->val == key) {
// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点
if (root->left == nullptr) return root->right;
// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
else if (root->right == nullptr) return root->left;
// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
else {
TreeNode* cur = root->right; // 找右子树最左面的节点
while(cur->left != nullptr) {
cur = cur->left;
}
cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置
TreeNode* tmp = root; // 把root节点保存一下,下面来删除
root = root->right; // 返回旧root的右孩子作为新root
delete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)
return root;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
//另一种方法
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key)
{
if (root == nullptr) return root;
if (root->val == key) {
if (root->right == nullptr) { // 这里第二次操作目标值:最终删除的作用
return root->left;
}
TreeNode *cur = root->right;
while (cur->left) {
cur = cur->left;
}
swap(root->val, cur->val); // 这里第一次操作目标值:交换目标值其右子树最左节点。
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
783. 二叉搜索树节点最小距离
难度简单193
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
示例 1:
输入:root = [4,2,6,1,3]
输出:1
示例 2:
输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
- 树中节点数目在范围
[2, 100]内 0 <= Node.val <= 105- 差值是一个正数,其数值等于两值之差的绝对值
题解
//递归
class Solution {
public:
TreeNode *pre=nullptr;
int ans=INT_MAX;
void dfs(TreeNode* root){
if(!root)return ;
dfs(root->left);
if(pre) ans=min(root->val-pre->val,ans);
pre=root;
dfs(root->right);
}
int minDiffInBST(TreeNode* root) {
dfs(root);
return ans;
}
};
//迭代
class Solution {
public:
TreeNode *pre=nullptr;
int ans=INT_MAX;
stack<TreeNode*>s;
int minDiffInBST(TreeNode* root) {
while(root||!s.empty()){
while(root){
s.push(root);
root=root->left;
}
root = s.top();s.pop();
if(pre) ans = min(root->val-pre->val,ans);
pre = root;
root=root->right;
}
return ans;
}
};
98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
题解
//迭代
class Solution {
public:
//TreeNode *pre=nullptr;
stack<TreeNode*>s;
bool isValidBST(TreeNode* root) {
if(!root)return true;
long cur =LONG_MIN;
while(root||!s.empty()){
while(root){
s.push(root);
root=root->left;
}
root=s.top();s.pop();
if(cur>= root->val) return false;
cur = root->val;
root=root->right;
}
return true;
}
};
//递归
class Solution {
public:
TreeNode *pre=nullptr;
bool isValidBST(TreeNode* root) {
if(!root)return true;
if(!isValidBST(root->left))return false;
if(pre&&root->val<=pre->val)return false;
pre =root;
if(!isValidBST(root->right))return false;
return true;
}
};
230. 二叉搜索树中第K小的元素
难度中等409收藏分享切换为英文接收动态反馈
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
题解
class Solution {
public:
stack<TreeNode*>s;
int kthSmallest(TreeNode* root, int k) {
if(!root)return 0;
while(root||!s.empty()){
while(root){
s.push(root);
root=root->left;
}
root=s.top();s.pop();
k--;
if(k==0)return root->val;
root=root->right;
}
return 0;
}
};
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
提示:
数组长度 <= 1000
题解
class Solution {
public:
bool verifyPostorder(vector<int>& p) {
stack<int>s;
int pre=INT_MAX;
for(int i=p.size()-1;i>=0;i--){
if(p[i]>pre)return false;
while(!s.empty()&&p[i]<s.top()){pre=s.top();s.pop();}
s.push(p[i]);
}
return true;
}
};
669. 修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构(即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在唯一的答案。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
示例 3:
输入:root = [1], low = 1, high = 2
输出:[1]
示例 4:
输入:root = [1,null,2], low = 1, high = 3
输出:[1,null,2]
示例 5:
输入:root = [1,null,2], low = 2, high = 4
输出:[2]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是唯一的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root)return root;
if(root->val<low) return trimBST(root->right,low,high);
if(root->val>high) return trimBST(root->left,low,high);
root->left = trimBST(root->left,low,high);
root->right = trimBST(root->right,low,high);
return root;
}
1382. 将二叉搜索树变平衡
难度中等67
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。
如果一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1 ,我们就称这棵二叉搜索树是 平衡的 。
如果有多种构造方法,请你返回任意一种。
示例:
输入:root = [1,null,2,null,3,null,4,null,null]
输出:[2,1,3,null,null,null,4]
解释:这不是唯一的正确答案,[3,1,4,null,2,null,null] 也是一个可行的构造方案。
提示:
- 树节点的数目在
1到10^4之间。 - 树节点的值互不相同,且在
1到10^5之间。
题解
class Solution {
public:
void inorder(TreeNode* root, vector<TreeNode*>& seq) {
if (!root) return ;
if (root->left) inorder(root->left,seq);
seq.emplace_back(root);
if (root->right) inorder(root->right,seq);
}
TreeNode* build(vector<TreeNode*>& seq, int l, int r) {
if (l>r) return NULL;
int m=(l+r)>>1;
TreeNode* root=seq[m];
root->left=build(seq, l, m-1);
root->right=build(seq, m+1, r);
return root;
}
TreeNode* balanceBST(TreeNode* root) {
vector<TreeNode*> seq;
inorder(root,seq);
return build(seq, 0, seq.size()-1);
}
};
剑指 Offer 36. 二叉搜索树与双向链表
难度中等276
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
题解
class Solution {
public:
void build(Node* root, Node* &head, Node *&tail) {//指针类型,你可以访问head 指针指向的区域,不能更改指针指向的地址 指针引用类型,除了可以访问指针指向的区域,还可以更改指针指向的地址, 因为后续代码中有做 head = root 这样的操作,所以更改了指针地址,所以用指针引用
if (root) {
build(root->left, head, tail);
if (head == nullptr) {//头节点为空
head = tail = root;
} else {
tail->right = root;
root->left = tail;
tail = root;
}
build(root->right, head, tail);
}
}
Node* treeToDoublyList(Node* root) {
if (root == nullptr) return nullptr;
Node *head = nullptr, *tail = nullptr;
build(root, head, tail);
head->left = tail;
tail->right = head;
return head;
}
};
◉ 十二、DFS和BFS
剑指 Offer 12. 矩阵中的路径
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 “ABCCED”(单词中的字母已标出)。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
提示:
1 <= board.length <= 2001 <= board[i].length <= 200board和word仅由大小写英文字母组成
int m;
int n;
bool dfs(const string &s,vector<vector<char>>& board,vector<vector<int>>&visit,int i,int j,int idx){
if(i<0||j<0||i>=m||j>=n||visit[i][j]||board[i][j]!=s[idx]){ return false;}
if(idx==(s.size()-1))return true;
visit[i][j]=1;
bool res=dfs(s,board,visit,i+1,j,idx+1)||dfs(s,board,visit,i-1,j,idx+1)||dfs(s,board,visit,i,j+1,idx+1)||dfs(s,board,visit,i,j-1,idx+1);
visit[i][j]=0;
return res;
}
bool exist(vector<vector<char>>& board,const string& word) {
m=board.size();
n=board[0].size();
if(((m)*(n))<word.size())return false; //剪枝
vector<vector<int> >visit(m,vector<int>(n,0));
for(int i=0;i<m;++i){
for(int j=0;j<n;++j){
if(dfs(word,board,visit,i,j,0)) return true;
}
}
return false;
}
22. 括号生成
难度中等1954
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
提示:
1 <= n <= 8
题解
//dfs
void dfs(string path,int l,int r){
if(l==0&&r==0){
ans.emplace_back(path);
return ;
}
if(l>0)dfs(path+"(",l-1,r);
if(r>l)dfs(path+")",l,r-1);
}
//bfs:记忆化搜索
class Solution {
public:
vector<string> ans;
struct node{
node(string s1,int l1,int r1):s(s1),l(l1),r(r1){}
string s;
int l;
int r;
};
void bfs(string path,int l,int r){
queue<node> q;
q.emplace(node(path,l,r));
while(!q.empty()) {
auto temp=q.front();
q.pop();
if(temp.l==0&&temp.r==0) ans.emplace_back(temp.s);
if(temp.l>0) q.emplace(node(temp.s+"(",temp.l-1,temp.r));
if(temp.r>temp.l) q.emplace(node(temp.s+")",temp.l,temp.r-1));
}
}
vector<string> generateParenthesis(int n) {
if(n<=0)return ans;
bfs("",n,n);
return ans;
}
};
130. 被围绕的区域
难度中等561
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
题解
如果矩阵的四周都是X,那么矩阵中只要有O,肯定是被X包围的。否则,将边界的与O连通的块标记为A。
//dfs
class Solution {
public:
void dfs(vector<vector<char>>& board,int i,int j ){
if(i<0||j<0||i>=board.size()||j>=board[0].size()||board[i][j]!='O') return ;
board[i][j]='A';
dfs(board,i-1,j);//up
dfs(board,i+1,j);//down
dfs(board,i,j-1);//left
dfs(board,i,j+1);//right
}
void solve(vector<vector<char>>& board) {
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(i==0||j==0||i==board.size()-1||j==board[0].size()-1) //矩阵的四周
dfs(board,i,j); //mark the A flag
}
}
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]!='A') board[i][j]='X';
else board[i][j]='O';
}
}
return ;
}
};
//BFS
class Solution {
public:
void bfs(vector<vector<char>>& board,int i,int j ){
if(i<0||j<0||i>=board.size()||j>=board[0].size()||board[i][j]!='O') return ;
queue<pair<int,int>>q;
board[i][j]='A';
q.push(pair<int,int>(i,j));
pair<int,int>temp;
int ctrl[4][2]={{-1,0},{1,0},{0,-1},{0,1}};//方向控制
while(!q.empty()){
temp = q.front();q.pop();
for(int idx=0;idx<4;++idx){
int x=temp.first+ctrl[idx][0];
int y=temp.second+ctrl[idx][1];
if(x<0||y<0||x>=board.size()||y>=board[0].size()||board[x][y]!='O')
continue ;
board[x][y]='A';
q.push(pair<int,int>(x,y));
}
}
return ;
}
void solve(vector<vector<char>>& board) {
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(i==0||j==0||i==board.size()-1||j==board[0].size()-1)
bfs(board,i,j); //mark the A flag
}
}
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]!='A') board[i][j]='X';
else board[i][j]='O';
}
}
return ;
}
};
剑指 Offer 13. 机器人的运动范围
难度中等315收藏分享切换为英文接收动态反馈
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 1000 <= k <= 20
题解
//dfs
class Solution {
public:
int ans=0;
bool isValid(int i, int j,int k){
int sum=0;
while(i){
sum+=(i%10);
i/=10;
}
while(j){
sum+=(j%10);
j/=10;
}
return sum>k;
}
void dfs(int i, int j,int k,vector<vector<int>>&m){ //区别部分
if(i<0||j<0||i>=m.size()||j>=m[0].size()||m[i][j]==0||isValid(i,j,k)) return ;
m[i][j]=0;
ans++;
dfs(i-1,j,k,m);
dfs(i+1,j,k,m);
dfs(i,j-1,k,m);
dfs(i,j+1,k,m);
}
int movingCount(int ms, int ns, int k) {
vector<vector<int>> m(ms,vector<int>(ns,1));
dfs(0,0,k,m); //可以改为bfs
return ans;
}
};
//bfs 基本代码一样
void bfs(int i, int j,int k,vector<vector<int>>&m){
if(i<0||j<0||i>=m.size()||j>=m[0].size()||m[i][j]==0||isValid(i,j,k)) return ;
queue<pair<int,int>>q;
m[i][j]=0;
ans++;
pair<int,int>temp;
q.push(pair<int,int>(i,j));
int ctrl[4][2]={{-1,0},{1,0},{0,-1},{0,1}};//方向控制
while(!q.empty()){
temp=q.front(),q.pop();
for(int idx=0;idx<4;++idx){
int x=temp.first+ctrl[idx][0];
int y=temp.second+ctrl[idx][1];
if(x<0||y<0||x>=m.size()||y>=m[0].size()||m[x][y]==0||isValid(x,y,k)) continue;
m[x][y]=0;
ans++;
q.push(pair<int,int>(x,y));
}
}
}
200. 岛屿数量
难度中等1223
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
题解
直接在原数组进行标记,将0标记为已经访问。
//dfs
class Solution {
public:
void dfs(vector<vector<char>>& board,int i, int j){
if(i<0||j<0||i>=board.size()||j>=board[0].size()||board[i][j]=='0') return ;
board[i][j]='0';
dfs(board,i-1,j);//up
dfs(board,i+1,j);//down
dfs(board,i,j-1);//left
dfs(board,i,j+1);//right
}
int numIslands(vector<vector<char>>& board) {
int ans=0;
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]=='1') //矩阵的四周
{
dfs(board,i,j); //mark the A flag and that means the visited block
ans++;
}
}
}
return ans;
}
};
//bfs
class Solution {
public:
void bfs(vector<vector<char>>& board,int i, int j){
if(i<0||j<0||i>=board.size()||j>=board[0].size()||board[i][j]=='0') return ;
queue<pair<int,int>>q;
board[i][j]='0';
pair<int,int>temp;
q.push(pair<int,int>(i,j));
int ctrl[4][2]={{-1,0},{1,0},{0,-1},{0,1}};//方向控制
while(!q.empty()){
temp=q.front(),q.pop();
for(int idx=0;idx<4;idx++){
int x=temp.first+ctrl[idx][0];
int y=temp.second+ctrl[idx][1];
if(x<0||y<0||x>=board.size()||y>=board[0].size()||board[x][y]=='0') continue;
board[x][y]='0';
q.push(pair<int,int>(x,y));
}
}
return ;
}
int numIslands(vector<vector<char>>& board) {
int ans=0;
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]=='1') //矩阵的四周
{
bfs(board,i,j); //mark the A flag and that means the visited block
ans++;
}
}
}
return ans;
}
};
马的遍历
题目描述
有一个 n \times mn×m 的棋盘,在某个点 (x, y)(x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。
输入格式
输入只有一行四个整数,分别为 n, m, x, yn,m,x,y。
输出格式
一个 n \times mn×m 的矩阵,代表马到达某个点最少要走几步(左对齐,宽 55 格,不能到达则输出 -1−1)。
输入输出样例
**输入 **
3 3 1 1
输出
0 3 2
3 -1 1
2 1 4
题解
#include<iostream>//P1443
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
const int dx[8]={-1, -2, -2, -1, 1, 2, 2, 1};
const int dy[8]={ 2, 1, -1, -2, 2, 1, -1,-2};//8个方向
queue<pair<int,int> > q;
int f[500][500];//存步数
bool vis[500][500];//走没走过
int main()
{
int n,m,x,y;
memset(f,-1,sizeof(f)); //全为-1
memset(vis,false,sizeof(vis)); //全为false
cin>>n>>m>>x>>y;
f[x][y]=0;vis[x][y]=true;q.push(make_pair(x,y));
while(!q.empty())
{
int xx=q.front().first,yy=q.front().second;q.pop();//取队首并出队
for(int i=0;i<8;i++)
{
int u=xx+dx[i],v=yy+dy[i];
if(u<1||u>n||v<1||v>m||vis[u][v])continue;//出界或走过就不走
vis[u][v]=true;
q.push(make_pair(u,v));
f[u][v]=f[xx][yy]+1;
}
}
for(int i=1;i<=n;i++)
{for(int j=1;j<=m;j++)printf("%-5d",f[i][j]);printf("\n");}//注意场宽!!
return 0;
}
1905. 统计子岛屿
难度: 中等
给你两个 m x n 的二进制矩阵 grid1 和 grid2 ,它们只包含 0 (表示水域)和 1 (表示陆地)。一个 岛屿 是由 四个方向 (水平或者竖直)上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。
如果 grid2 的一个岛屿,被 grid1 的一个岛屿 完全 包含,也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含,那么我们称 grid2 中的这个岛屿为 子岛屿 。
请你返回 grid2 中 子岛屿 的 数目 。
示例 1:
输入:grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出:3
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 3 个子岛屿。
示例 2:
输入:grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
输出:2
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 2 个子岛屿。
提示:
m == grid1.length == grid2.lengthn == grid1[i].length == grid2[i].length1 <= m, n <= 500grid1[i][j]和grid2[i][j]都要么是0要么是1。
题解
//dfs
class Solution {
public:
bool f;
void dfs(int i,int j,vector<vector<int>>& grid1,vector<vector<int>>& grid2){
if(i<0||j<0||i>=grid2.size()||j>=grid2[0].size()||grid2[i][j]==0)return;
if(grid1[i][j]!=1)f=false;
grid2[i][j]=0;
dfs(i-1,j,grid1,grid2);
dfs(i+1,j,grid1,grid2);
dfs(i,j-1,grid1,grid2);
dfs(i,j+1,grid1,grid2);
}
int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
int ans=0;
for(int i=0;i<grid2.size();++i){
for(int j=0;j<grid2[0].size();++j){
if(grid2[i][j]==1) {
f=true;
dfs(i,j,grid1,grid2);
if(f)ans++;
}
}
}
return ans;
}
};
//bfs
void bfs(int i,int j,vector<vector<int>>& grid1,vector<vector<int>>& grid2){
if(i<0||j<0||i>=grid2.size()||j>=grid2[0].size()||grid2[i][j]==0)return;
if(grid1[i][j]!=1)f=false;
grid2[i][j]=0;
queue<pair<int,int>>q;
pair<int,int>temp;
q.push(pair<int,int>(i,j));
int ctrl[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
while(!q.empty()){
temp=q.front(),q.pop();
for(int idx=0;idx<4;++idx){
int x=temp.first+ctrl[idx][0];
int y=temp.second+ctrl[idx][1];
if(x<0||y<0||x>=grid2.size()||y>=grid2[0].size()||grid2[x][y]==0) continue;
if(grid1[x][y]!=1)f=false;
grid2[x][y]=0;
q.push(pair<int,int>(x,y));
}
}
}
695. 岛屿的最大面积
难度中等504收藏分享切换为英文接收动态反馈
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
示例 2:
[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。
题解
//dfs
class Solution {
public:
int dfs(vector<vector<int>>& grid,int i, int j){
if(i<0||j<0||i>=grid.size()||j>=grid[0].size()||grid[i][j]==0) return 0;
int c=1;
grid[i][j]=0;
c+=dfs(grid,i-1,j);
c+=dfs(grid,i+1,j);
c+=dfs(grid,i,j-1);
c+=dfs(grid,i,j+1);
return c;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans=0;
for(int i=0;i<grid.size();++i){
for(int j=0;j<grid[0].size();++j) {
if(grid[i][j]==1) ans = max(ans,dfs(grid,i,j));
}
}
return ans;
}
};
//bfs
class Solution {
public:
int bfs(vector<vector<int>>& grid,int i, int j){
if(i<0||j<0||i>=grid.size()||j>=grid[0].size()||grid[i][j]==0) return 0;
pair<int,int>temp;
queue<pair<int,int>>q;
grid[i][j]=0;
int c=1;
q.push(pair<int,int>(i,j));
int ctrl[4][2]={{-1,0},{1,0},{0,-1},{0,1}};//方向控制
while(!q.empty()){
temp=q.front(),q.pop();
for(int idx=0;idx<4;++idx){
int x = temp.first+ctrl[idx][0];
int y = temp.second+ctrl[idx][1];
if(x<0||y<0||x>=grid.size()||y>=grid[0].size()||grid[x][y]==0) continue;
c++;
grid[x][y]=0;
q.push(pair<int,int>(x,y));
}
}
return c;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans=0;
for(int i=0;i<grid.size();++i){
for(int j=0;j<grid[0].size();++j) {
if(grid[i][j]==1) ans = max(ans,bfs(grid,i,j));
}
}
return ans;
}
};
LCP 07. 传递信息
难度: 简单
小朋友 A 在和 ta 的小伙伴们玩传信息游戏,游戏规则如下:
- 有 n 名玩家,所有玩家编号分别为 0 ~ n-1,其中小朋友 A 的编号为 0
- 每个玩家都有固定的若干个可传信息的其他玩家(也可能没有)。传信息的关系是单向的(比如 A 可以向 B 传信息,但 B 不能向 A 传信息)。
- 每轮信息必须需要传递给另一个人,且信息可重复经过同一个人
给定总玩家数 n,以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数;若不能到达,返回 0。
示例 1:
输入:
n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3输出:
3解释:信息从小 A 编号 0 处开始,经 3 轮传递,到达编号 4。共有 3 种方案,分别是 0->2->0->4, 0->2->1->4, 0->2->3->4。
示例 2:
输入:
n = 3, relation = [[0,2],[2,1]], k = 2输出:
0解释:信息不能从小 A 处经过 2 轮传递到编号 2
限制:
2 <= n <= 101 <= k <= 51 <= relation.length <= 90, 且 relation[i].length == 20 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]
题解
//DFS
class Solution {
public:
int ans = 0;
int numWays(int n, vector<vector<int>>& relation, int k) {
for(int i = 0; i < relation.size(); i++){
if(relation[i][0] == 0)
dfs(relation, relation[i][1], 1, k, n);
}
return ans;
}
void dfs(vector<vector<int>>& relation, int start, int step, int k, int n){
if(step == k){
if(start == n-1)
ans++;
return;
}
for(int i = 0; i < relation.size(); i++){
if(relation[i][0] == start)
dfs(relation, relation[i][1], step+1, k, n);
}
}
};
//DP
class Solution {
public:
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<vector<int>> dp(k + 1, vector<int>(n));
dp[0][0] = 1;
for (int i = 0; i < k; i++) {
for (auto& edge : relation) {
int src = edge[0], dst = edge[1];
dp[i + 1][dst] += dp[i][src];
}
}
return dp[k][n - 1];
}
};
//优化DP
class Solution {
public:
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<int> dp(n);
dp[0] = 1;
for (int i = 0; i < k; i++) {
vector<int> next(n);
for (auto& edge : relation) {
int src = edge[0], dst = edge[1];
next[dst] += dp[src];
}
dp = next;
}
return dp[n - 1];
}
};
752. 打开转盘锁
难度中等359收藏分享切换为英文接收动态反馈
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9'。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:
把最后一位反向旋转一次即可 "0000" -> "0009"。
示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:
无法旋转到目标数字且不被锁定。
示例 4:
输入: deadends = ["0000"], target = "8888"
输出:-1
提示:
1 <= deadends.length <= 500deadends[i].length == 4target.length == 4target不在deadends之中target和deadends[i]仅由若干位数字组成
题解
static int x=[](){
ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
class Solution {
public:
int openLock(vector<string>& deadends, const string& target) {
unordered_set<string>v(deadends.begin(),deadends.end());
if(v.count("0000"))return -1;//剪枝
queue<string>q;
q.push("0000"); //根节点
int ans=0;
while(!q.empty()){
int len=q.size();
for(int i=0;i<len;++i){
string temp=q.front();q.pop();
if(temp==target)return ans;
for(int j=0;j<4;++j){
for(int k=-1;k<2;k+=2){
char y=(temp[j]-'0'+10+k)%10+'0';//翻键
string x=temp;
x[j]=y;
if(!v.count(x)){
q.push(x);
v.emplace(x);
}
}
}
}
ans++;
}
return -1;
}
};
127. 单词接龙
难度困难794收藏分享切换为英文接收动态反馈
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。 - 序列中最后一个单词是
endWord。 - 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10endWord.length == beginWord.length1 <= wordList.length <= 5000wordList[i].length == beginWord.lengthbeginWord、endWord和wordList[i]由小写英文字母组成beginWord != endWordwordList中的所有字符串 互不相同
题解
class Solution {
public:
queue<string> q;
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
q.push(beginWord);
int res = 0;
string s;
while(!q.empty()){
res++;
for(int idx = q.size(); idx > 0; idx--){
s = q.front();q.pop();
if(s == endWord) return res;
for(string & w: wordList){
if(w.empty() || w.length() != beginWord.length()) continue;
int diff = 0;
for(int i = 0; i < w.length(); i++){//比较差异
if(w[i] != s[i]) ++diff;
if(diff > 1) break;
}
if(diff <= 1){
q.push(w);
w = "";//visited
}
}
}
}
return 0;
}
};
120. 三角形最小路径和
难度中等788
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
题解
//DFS
class Solution {
public:
int dfs(vector<vector<int>>&m,vector<vector<int>>& triangle,int i, int j){
if(i==m.size()) return 0;
if(m[i][j])return triangle[i][j];
return min(dfs(m,triangle, i+1,j),dfs(m,triangle, i+1,j+1))+triangle[i][j];
}
int minimumTotal(vector<vector<int>>& triangle) {
vector<vector<int>>m(triangle.size(),vector<int>(triangle.size(),0));
return dfs(m,triangle,0,0);
}
};
//dp
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<int> dp(triangle.back());
for(int i = triangle.size() - 2; i >= 0; i --)
for(int j = 0; j <= i; j ++)
dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
return dp[0];
}
};
1306. 跳跃游戏 III
难度中等77
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2
输出:false
解释:无法到达值为 0 的下标 1 处。
提示:
1 <= arr.length <= 5 * 10^40 <= arr[i] < arr.length0 <= start < arr.length
题解
//dfs
class Solution {
public:
bool dfs(vector<int>& arr,int start){
if(start<0||start>=arr.size()||arr[start]==-1) return false;
int step=arr[start];
arr[start]=-1;
return step==0||dfs(arr,start+step) ||dfs(arr,start-step) ;
}
bool canReach(vector<int>& arr, int start) {
return dfs(arr,start);
}
};
//bfs
class Solution {
public:
bool bfs(vector<int>& arr,int start){
if(start<0||start>arr.size())return false;
queue<int>q;
unordered_set<int> v;
q.push(start); //保存index
int temp;
v.emplace(start);
while(!q.empty()) {
temp = q.front(),q.pop();
if(arr[temp]==0) return true;
int step1=temp+arr[temp];
if(step1>=0 && step1<arr.size() && !v.count(step1)){
q.push(step1);
v.emplace(step1);
}
int step2=temp-arr[temp];
if(step2>=0 && step2<arr.size() && !v.count(step2)){
q.push(step2);
v.emplace(step2);
}
}
return false;
}
bool canReach(vector<int>& arr, int start) {
return bfs(arr,start);
}
};
542. 01 矩阵
难度中等446
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:
[[0,0,0],
[0,1,0],
[0,0,0]]
输出:
[[0,0,0],
[0,1,0],
[0,0,0]]
示例 2:
输入:
[[0,0,0],
[0,1,0],
[1,1,1]]
输出:
[[0,0,0],
[0,1,0],
[1,2,1]]
提示:
- 给定矩阵的元素个数不超过 10000。
- 给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
题解
//bfs
struct P{
int x, y, dis;
};
class Solution {
public:
int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
queue<P> q;
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> vis(m, vector<int>(n, 0));
vector<vector<int>> res(m, vector<int>(n, 0));
for(int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if(matrix[i][j] == 0) q.push({i, j, 0}), vis[i][j] = 1;
while(!q.empty())
{
P t = q.front();
q.pop();
int x = t.x, y = t.y, d = t.dis;
vis[x][y] = 1;
for(int k = 0; k < 4; k++)
{
int nx = x + dx[k], ny = y + dy[k];
if(nx<0 || nx>=m || ny<0 || ny>=n || vis[nx][ny]) continue;
q.push({nx, ny, d + 1});
res[nx][ny] = d + 1;
vis[nx][ny] = 1;
}
}
return res;
}
};
//dp
class Solution {
public:
int row,col;
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
row = matrix.size();
col = matrix[0].size();
vector <vector <int>> dp(row,vector <int>(col,INT_MAX/10));
for (int i=0;i<row;i++){
for (int j=0;j<col;j++){
if (matrix[i][j] == 0)
dp[i][j] = 0;
else{
if (i>0) dp[i][j] = min(dp[i][j],dp[i-1][j]+1);
if (j>0) dp[i][j] = min(dp[i][j],dp[i][j-1]+1);
} }
}
for (int i=row - 1;i>=0;i--){
for (int j=col - 1;j>=0;j--){
if (i < row - 1)
dp[i][j] = min(dp[i][j],dp[i+1][j]+1);
if (j < col - 1)
dp[i][j] = min(dp[i][j],dp[i][j+1]+1);
}
}
return dp;
}
};
994. 腐烂的橘子
难度中等379收藏分享切换为英文接收动态反馈
在给定的网格中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:
输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:[[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:[[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j]仅为0、1或2
题解
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int row = grid.size(); //grid的行数
int column = grid[0].size(); //grid的列数
int ans = -1; //初始置为-1
int moverow[4] = {-1,0,0,1}; //对于(i,j)它的上下左右分别为(i-1,j),(1,0),(0,-1),(0,1)
int movecolumn[4] = {0,-1,1,0}; //因此在这里设置两个数组分别代表(i,j)相邻的4个结点
//从而避免之后不断的利用if判断i-1,i+1,j-1,j+1是否越界
int numberof1 = 0; //1的个数
int numberof2 = 0; //2的个数
queue<pair<int,int>> orange;
for(int i=0;i<row;i++){ //统计1,2的个数,并把腐烂的橘子压入队列
for(int j = 0;j<column;j++){
if(grid[i][j]==2){
orange.push(make_pair(i,j));
numberof2++;
}
if(grid[i][j]==1) numberof1++;
}
}
if(numberof2==0&&numberof1==0) return 0; //如果没有腐烂的橘子且没有新鲜的橘子则返回0
//如果没有腐烂的橘子但是有新鲜的橘子则返回-1,不过这里不用判断此情况,因为之后的代码会识别出此情况
while(!orange.empty()){ //队列非空要执行操作
int queuelen = orange.size(); //判断此时队列的长度,当执行了queuelen次后,相当于过了一天
for(int k=0;k<queuelen;k++){
int x = orange.front().first; //获取腐烂橘子的横坐标
int y = orange.front().second; //获取纵坐标
orange.pop(); //弹出队列
for(int i=0;i<4;i++){ //共上下左右4种情况
int newx = x + moverow[i];
int newy = y + movecolumn[i];
if(newx>=0&&newx<row&&newy>=0&&newy<column&&grid[newx][newy]==1){ //判断是否越界
//注意这里与的顺序,由于先判断越界,后执行grid[newx][newy],因此一旦越界便不再判断grid[newx][newy]==1
orange.push(make_pair(newx,newy)); //将紧挨腐烂橘子的新鲜橘子压入队列
grid[newx][newy] = 2; //置为腐烂的橘子,防止同一个橘子不断压入队列陷入死循环
numberof1--; //新鲜的个数减1
}
if(!numberof1) break;
}
}
ans++; //在执行了queuelen次后,相当于过了一天,结果加一
}
return numberof1 ? -1 : ans;
}
};
◉ 十三、字符串匹配和分割
1.istringstream
void split1(vector<string> &res, const string& str, const char& pattern=' '){
//头文件<sstream>
istringstream is(str);
string temp;
while(getline(is,temp,pattern)){
res.emplace_back(temp);
}
return ;
}
//调用格式:const char dlim = ',' ; split(res,str,dlim);
2.strtok
void split2(vector<string>& res,const string& str,const char* pattern=" ")
{
//头文件<cstring>
//***1.强制转换和调用strtok()***
char* p=strtok(const_cast<char*>(str.c_str()),pattern) ;
while(p){
res.push_back(p);
p =strtok(NULL,pattern);
}
return;
}
//调用格式:const char* dlim =","; split(res,str,dlim);
139. 单词拆分
难度中等1044
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
- 拆分时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
et<string>v(deadends.begin(),deadends.end());
if(v.count("0000"))return -1;//剪枝
queue<string>q;
q.push("0000"); //根节点
int ans=0;
while(!q.empty()){
int len=q.size();
for(int i=0;i<len;++i){
string temp=q.front();q.pop();
if(temp==target)return ans;
for(int j=0;j<4;++j){
for(int k=-1;k<2;k+=2){
char y=(temp[j]-'0'+10+k)%10+'0';//翻键
string x=temp;
x[j]=y;
if(!v.count(x)){
q.push(x);
v.emplace(x);
}
}
}
}
ans++;
}
return -1;
}
};
127. 单词接龙
难度困难794收藏分享切换为英文接收动态反馈
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。 - 序列中最后一个单词是
endWord。 - 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10endWord.length == beginWord.length1 <= wordList.length <= 5000wordList[i].length == beginWord.lengthbeginWord、endWord和wordList[i]由小写英文字母组成beginWord != endWordwordList中的所有字符串 互不相同
题解
class Solution {
public:
queue<string> q;
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
q.push(beginWord);
int res = 0;
string s;
while(!q.empty()){
res++;
for(int idx = q.size(); idx > 0; idx--){
s = q.front();q.pop();
if(s == endWord) return res;
for(string & w: wordList){
if(w.empty() || w.length() != beginWord.length()) continue;
int diff = 0;
for(int i = 0; i < w.length(); i++){//比较差异
if(w[i] != s[i]) ++diff;
if(diff > 1) break;
}
if(diff <= 1){
q.push(w);
w = "";//visited
}
}
}
}
return 0;
}
};
120. 三角形最小路径和
难度中等788
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
题解
//DFS
class Solution {
public:
int dfs(vector<vector<int>>&m,vector<vector<int>>& triangle,int i, int j){
if(i==m.size()) return 0;
if(m[i][j])return triangle[i][j];
return min(dfs(m,triangle, i+1,j),dfs(m,triangle, i+1,j+1))+triangle[i][j];
}
int minimumTotal(vector<vector<int>>& triangle) {
vector<vector<int>>m(triangle.size(),vector<int>(triangle.size(),0));
return dfs(m,triangle,0,0);
}
};
//dp
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<int> dp(triangle.back());
for(int i = triangle.size() - 2; i >= 0; i --)
for(int j = 0; j <= i; j ++)
dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
return dp[0];
}
};
1306. 跳跃游戏 III
难度中等77
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2
输出:false
解释:无法到达值为 0 的下标 1 处。
提示:
1 <= arr.length <= 5 * 10^40 <= arr[i] < arr.length0 <= start < arr.length
题解
//dfs
class Solution {
public:
bool dfs(vector<int>& arr,int start){
if(start<0||start>=arr.size()||arr[start]==-1) return false;
int step=arr[start];
arr[start]=-1;
return step==0||dfs(arr,start+step) ||dfs(arr,start-step) ;
}
bool canReach(vector<int>& arr, int start) {
return dfs(arr,start);
}
};
//bfs
class Solution {
public:
bool bfs(vector<int>& arr,int start){
if(start<0||start>arr.size())return false;
queue<int>q;
unordered_set<int> v;
q.push(start); //保存index
int temp;
v.emplace(start);
while(!q.empty()) {
temp = q.front(),q.pop();
if(arr[temp]==0) return true;
int step1=temp+arr[temp];
if(step1>=0 && step1<arr.size() && !v.count(step1)){
q.push(step1);
v.emplace(step1);
}
int step2=temp-arr[temp];
if(step2>=0 && step2<arr.size() && !v.count(step2)){
q.push(step2);
v.emplace(step2);
}
}
return false;
}
bool canReach(vector<int>& arr, int start) {
return bfs(arr,start);
}
};
542. 01 矩阵
难度中等446
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:
[[0,0,0],
[0,1,0],
[0,0,0]]
输出:
[[0,0,0],
[0,1,0],
[0,0,0]]
示例 2:
输入:
[[0,0,0],
[0,1,0],
[1,1,1]]
输出:
[[0,0,0],
[0,1,0],
[1,2,1]]
提示:
- 给定矩阵的元素个数不超过 10000。
- 给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
题解
//bfs
struct P{
int x, y, dis;
};
class Solution {
public:
int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
queue<P> q;
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> vis(m, vector<int>(n, 0));
vector<vector<int>> res(m, vector<int>(n, 0));
for(int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if(matrix[i][j] == 0) q.push({i, j, 0}), vis[i][j] = 1;
while(!q.empty())
{
P t = q.front();
q.pop();
int x = t.x, y = t.y, d = t.dis;
vis[x][y] = 1;
for(int k = 0; k < 4; k++)
{
int nx = x + dx[k], ny = y + dy[k];
if(nx<0 || nx>=m || ny<0 || ny>=n || vis[nx][ny]) continue;
q.push({nx, ny, d + 1});
res[nx][ny] = d + 1;
vis[nx][ny] = 1;
}
}
return res;
}
};
//dp
class Solution {
public:
int row,col;
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
row = matrix.size();
col = matrix[0].size();
vector <vector <int>> dp(row,vector <int>(col,INT_MAX/10));
for (int i=0;i<row;i++){
for (int j=0;j<col;j++){
if (matrix[i][j] == 0)
dp[i][j] = 0;
else{
if (i>0) dp[i][j] = min(dp[i][j],dp[i-1][j]+1);
if (j>0) dp[i][j] = min(dp[i][j],dp[i][j-1]+1);
} }
}
for (int i=row - 1;i>=0;i--){
for (int j=col - 1;j>=0;j--){
if (i < row - 1)
dp[i][j] = min(dp[i][j],dp[i+1][j]+1);
if (j < col - 1)
dp[i][j] = min(dp[i][j],dp[i][j+1]+1);
}
}
return dp;
}
};
994. 腐烂的橘子
难度中等379收藏分享切换为英文接收动态反馈
在给定的网格中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:
[外链图片转存中…(img-xxrW1W6P-1630453061673)]
输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:[[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:[[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j]仅为0、1或2
题解
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int row = grid.size(); //grid的行数
int column = grid[0].size(); //grid的列数
int ans = -1; //初始置为-1
int moverow[4] = {-1,0,0,1}; //对于(i,j)它的上下左右分别为(i-1,j),(1,0),(0,-1),(0,1)
int movecolumn[4] = {0,-1,1,0}; //因此在这里设置两个数组分别代表(i,j)相邻的4个结点
//从而避免之后不断的利用if判断i-1,i+1,j-1,j+1是否越界
int numberof1 = 0; //1的个数
int numberof2 = 0; //2的个数
queue<pair<int,int>> orange;
for(int i=0;i<row;i++){ //统计1,2的个数,并把腐烂的橘子压入队列
for(int j = 0;j<column;j++){
if(grid[i][j]==2){
orange.push(make_pair(i,j));
numberof2++;
}
if(grid[i][j]==1) numberof1++;
}
}
if(numberof2==0&&numberof1==0) return 0; //如果没有腐烂的橘子且没有新鲜的橘子则返回0
//如果没有腐烂的橘子但是有新鲜的橘子则返回-1,不过这里不用判断此情况,因为之后的代码会识别出此情况
while(!orange.empty()){ //队列非空要执行操作
int queuelen = orange.size(); //判断此时队列的长度,当执行了queuelen次后,相当于过了一天
for(int k=0;k<queuelen;k++){
int x = orange.front().first; //获取腐烂橘子的横坐标
int y = orange.front().second; //获取纵坐标
orange.pop(); //弹出队列
for(int i=0;i<4;i++){ //共上下左右4种情况
int newx = x + moverow[i];
int newy = y + movecolumn[i];
if(newx>=0&&newx<row&&newy>=0&&newy<column&&grid[newx][newy]==1){ //判断是否越界
//注意这里与的顺序,由于先判断越界,后执行grid[newx][newy],因此一旦越界便不再判断grid[newx][newy]==1
orange.push(make_pair(newx,newy)); //将紧挨腐烂橘子的新鲜橘子压入队列
g