1.引言
在之前的讨论中,我们构建了一个理论模型来表达最优决策规则,这是建立在我们对数据的概率模型有充分理解的基础上的。相对地,经验风险最小化(Empirical Risk Minimization, ERM)策略则在缺乏精确概率模型的情况下,借助数值方法来发掘有效的决策规则。本章将深入探讨如何高效解决经验风险最小化问题,重点介绍解决这类问题时常用的核心优化方法,以及分析这些方法执行时间所需的数学工具。
本文的焦点是梯度下降算法,以及如何巧妙设计损失函数以确保梯度下降法能够成功找到解决方案。梯度下降法是一种迭代算法,它在可能的模型集合中进行选择,每一步都将当前模型替换为一个具有更低经验风险的新模型。我们将证明,当优化问题属于凸函数集合时,梯度下降法能够保证找到全局最优解。在风险最小化的背景下,这意味着只要损失函数是凸的,并且决策函数是特征的线性组合,梯度下降法就能够找到最小化经验风险的模型。
接下来,我们将研究随机梯度下降(Stochastic Gradient Descent, SGD),这是机器学习中的核心工具。SGD实际上是对感知机学习规则的一种扩展。它的通用性允许我们将SGD应用于多种不同的函数类别和损失函数,并确保即便数据不可分离,算法也能收敛。我们将花费相当篇幅来探讨SGD的动态特性,以期理解其在机器学习中广受欢迎并取得成功的原因。
从凸问题的讨论出发,我们将进一步探索更一般的非凸问题。特别是,我们将强调梯度下降和随机梯度下降在经验风险最小化中的两个突出特点,这些特点有助于解释这些方法的鲁棒性。
首先,我们将展示即使在非凸问题中,经验风险最小化的梯度下降也具有一种隐含的凸性质,这种性质有助于促进算法的收敛。尽管我们优化的函数表示在最坏情况下可能是计算上不可行的,但我们仍然能够对预测本身的收敛性进行推理。
其次,我们将证明梯度下降能够在优化过程中隐式地管理预测函数的复杂性,这在存在无限多解的情况下,有助于鼓励选择复杂性较低的解决方案。
最后,本文将以对其他经验风险最小化方法的讨论结束,这些方法更明确地考虑了模型复杂性以及稳定收敛的需求。通过这些讨论,我们希望能够为读者提供一个关于如何选择和应用不同优化策略的全面视角。
2.优化基础概述
2.1.命题和定义
让我们暂时将焦点从经验风险最小化问题上移开,转而思考一个更普遍的优化问题:
min
w
Φ
(
w
)
\min_{w} \Phi(w)
minwΦ(w)
这里,
Φ
:
R
d
→
R
\Phi: \mathbb{R}^d \rightarrow \mathbb{R}
Φ:Rd→R 是定义在
R
d
\mathbb{R}^d
Rd 上的实值函数。我们应在何种条件下、通过什么方法来最小化此类函数呢?在解答这些问题之前,我们需要先明确我们所追求的目标。
定义 5:最小化解
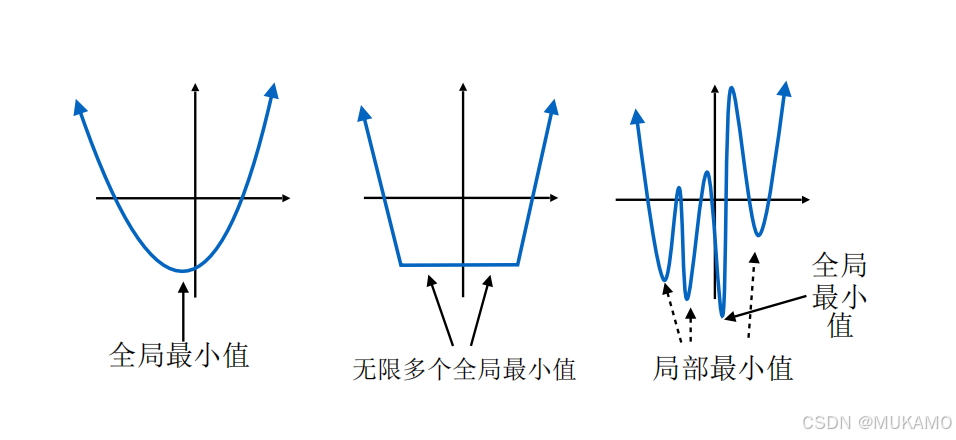
如果存在一个点 w ∗ w^* w∗ 满足对所有 w w w 都有 Φ ( w ∗ ) ≤ Φ ( w ) \Phi(w^*) \leq \Phi(w) Φ(w∗)≤Φ(w),则称 w ∗ w^* w∗ 是 Φ \Phi Φ 的一个最小化解。如果存在 e > 0 e > 0 e>0 使得对所有满足 ∥ w − w ∗ ∥ ≤ e \|w - w^*\| \leq e ∥w−w∗∥≤e 的 w w w 都有 Φ ( w ∗ ) ≤ Φ ( w ) \Phi(w^*) \leq \Phi(w) Φ(w∗)≤Φ(w),则称 w ∗ w^* w∗ 是 Φ \Phi Φ 的局部最小化解。有时,我们也会将全局最小化解与局部最小化解进行对比。
举例来说,下图中的函数展示了不同的最小值情形。在第一个例子中,存在一个唯一的最小化解。在第二个例子中,有无限多个最小化解,且所有局部最小化解也都是全局最小化解。而在第三个例子中,许多局部最小化解并不是全局最小化解。
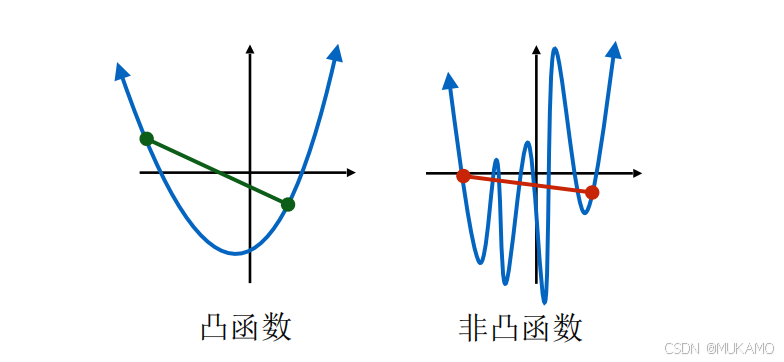
在这些例子中,没有次优局部最小化解的两个函数都有一个共同特性:对于任意两点 w 1 w_1 w1 和 w 2 w_2 w2,连接这两点的线段 ( w 1 , Φ ( w 1 ) ) (w_1, \Phi(w_1)) (w1,Φ(w1)) 到 ( w 2 , Φ ( w 2 ) ) (w_2, \Phi(w_2)) (w2,Φ(w2)) 完全位于函数图像的上方。这类函数我们称之为凸函数。
定义 6:凸函数
如果一个函数
Φ
\Phi
Φ 对于所有的
w
1
,
w
2
∈
R
d
w_1, w_2 \in \mathbb{R}^d
w1,w2∈Rd 和
α
∈
[
0
,
1
]
\alpha \in [0, 1]
α∈[0,1] 满足以下条件:
Φ
(
α
w
1
+
(
1
−
α
)
w
2
)
≤
α
Φ
(
w
1
)
+
(
1
−
α
)
Φ
(
w
2
)
\Phi(\alpha w_1 + (1 - \alpha)w_2) \leq \alpha \Phi(w_1) + (1 - \alpha)\Phi(w_2)
Φ(αw1+(1−α)w2)≤αΦ(w1)+(1−α)Φ(w2)
则称
Φ
\Phi
Φ 是凸函数。我们很快将看到,凸函数是一类特殊的函数,对于这类函数,梯度下降法能够保证找到最优解。
假设我们要最小化一个可微函数 Φ : R d → R \Phi: \mathbb{R}^d \rightarrow \mathbb{R} Φ:Rd→R。我们考虑的大多数算法都是从某点 w 0 w_0 w0 开始,然后尝试找到一个新点 w 1 w_1 w1,其函数值更低。最简单的方法是找到一个方向 v v v,使得沿此方向 Φ \Phi Φ 会减少。这个概念可以形式化为以下定义:
定义 7:下降方向
如果存在某个 t > 0 t > 0 t>0 使得 Φ ( w 0 + t v ) < Φ ( w 0 ) \Phi(w_0 + tv) < \Phi(w_0) Φ(w0+tv)<Φ(w0),则称 v v v 是 Φ \Phi Φ 在 w 0 w_0 w0 处的一个下降方向。
对于连续可微函数,判断
v
v
v 是否为下降方向非常简单:如果
v
T
∇
Φ
(
w
0
)
<
0
v^T \nabla \Phi(w_0) < 0
vT∇Φ(w0)<0,则
v
v
v 就是一个下降方向。这一点可以通过泰勒定理来理解:
Φ
(
w
0
+
α
v
)
=
Φ
(
w
0
)
+
α
∇
Φ
(
w
0
+
α
~
v
)
T
v
\Phi(w_0 + \alpha v) = \Phi(w_0) + \alpha \nabla \Phi(w_0 + \tilde{\alpha} v)^T v
Φ(w0+αv)=Φ(w0)+α∇Φ(w0+α~v)Tv
对于某个
α
~
∈
[
0
,
α
]
\tilde{\alpha} \in [0, \alpha]
α~∈[0,α]。如果
α
\alpha
α 很小,由于连续性,我们将有
∇
Φ
(
w
0
+
α
~
v
)
T
v
<
0
\nabla \Phi(w_0 + \tilde{\alpha} v)^T v < 0
∇Φ(w0+α~v)Tv<0。因此
Φ
(
w
0
+
α
v
)
<
Φ
(
w
0
)
\Phi(w_0 + \alpha v) < \Phi(w_0)
Φ(w0+αv)<Φ(w0) 且
v
v
v 是一个下降方向。
这种下降方向的特征使我们能够确定 w w w 最小化 Φ \Phi Φ 的条件。
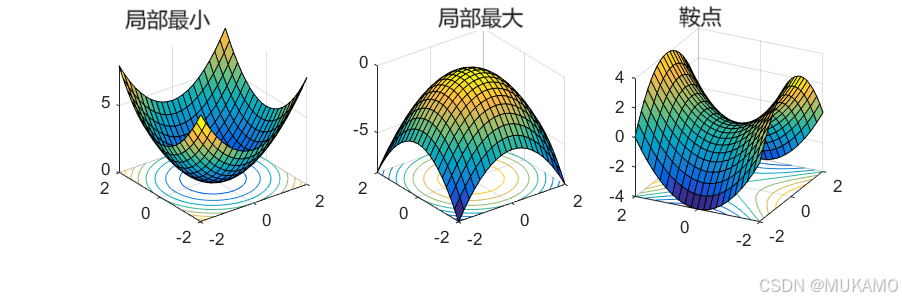
命题 4:局部最小化解
如果 w ∗ w^* w∗ 是 Φ \Phi Φ 的局部最小化解,那么必须有 ∇ Φ ( w ∗ ) = 0 \nabla \Phi(w^*) = 0 ∇Φ(w∗)=0。
这个命题的原因是,如果 − ∇ Φ ( w ∗ ) -\nabla \Phi(w^*) −∇Φ(w∗) 不为零,它总是一个下降方向。如果 w ∗ w^* w∗ 是局部最小值,那么就不可能存在下降方向。因此,梯度必须为零。
梯度下降算法基于这样一个事实:负梯度总是一个下降方向,来构建一个迭代过程:反复计算梯度并朝相反方向迈出一步以最小化 Φ \Phi Φ。当梯度变得足够小以至于迭代值 w t w_t wt 不再发生实质性变化时,梯度下降就会终止。但要注意,有些点梯度为零但函数并未最小化,例如,极大值点就具有这一属性。一般来说,梯度为零的点称为静止点。至关重要的是,并非所有静止点都是最小化解。
对于凸函数
Φ
\Phi
Φ,情况就简单多了。这也是凸性如此吸引人的原因之一。
命题 5:全局最小化解
设 Φ : R d → R \Phi : \mathbb{R}^d \rightarrow \mathbb{R} Φ:Rd→R 是一个可微凸函数。则 w ∗ w^* w∗ 是 Φ \Phi Φ 的全局最小化解当且仅当 ∇ Φ ( w ∗ ) = 0 \nabla \Phi(w^*) = 0 ∇Φ(w∗)=0。
证明:要证明这一点,我们需要使用凸性的定义:对于任何
α
∈
[
0
,
1
]
\alpha \in [0, 1]
α∈[0,1] 和
w
∈
R
d
w \in \mathbb{R}^d
w∈Rd,
Φ
(
w
∗
+
α
(
w
−
w
∗
)
)
≤
(
1
−
α
)
Φ
(
w
∗
)
+
α
Φ
(
w
)
\Phi(w^* + \alpha(w - w^*)) \leq (1 - \alpha)\Phi(w^*) + \alpha \Phi(w)
Φ(w∗+α(w−w∗))≤(1−α)Φ(w∗)+αΦ(w)
如果我们重新排列项,我们得到
Φ
(
w
)
≥
Φ
(
w
∗
)
+
∇
Φ
(
w
∗
)
T
(
w
−
w
∗
)
\Phi(w) \geq \Phi(w^*) + \nabla \Phi(w^*)^T (w - w^*)
Φ(w)≥Φ(w∗)+∇Φ(w∗)T(w−w∗)
如果
∇
Φ
(
w
∗
)
=
0
\nabla \Phi(w^*) = 0
∇Φ(w∗)=0,则
Φ
(
w
)
≥
Φ
(
w
∗
)
\Phi(w) \geq \Phi(w^*)
Φ(w)≥Φ(w∗) 对所有
w
w
w 成立,因此
w
∗
w^*
w∗ 是全局最小化解。
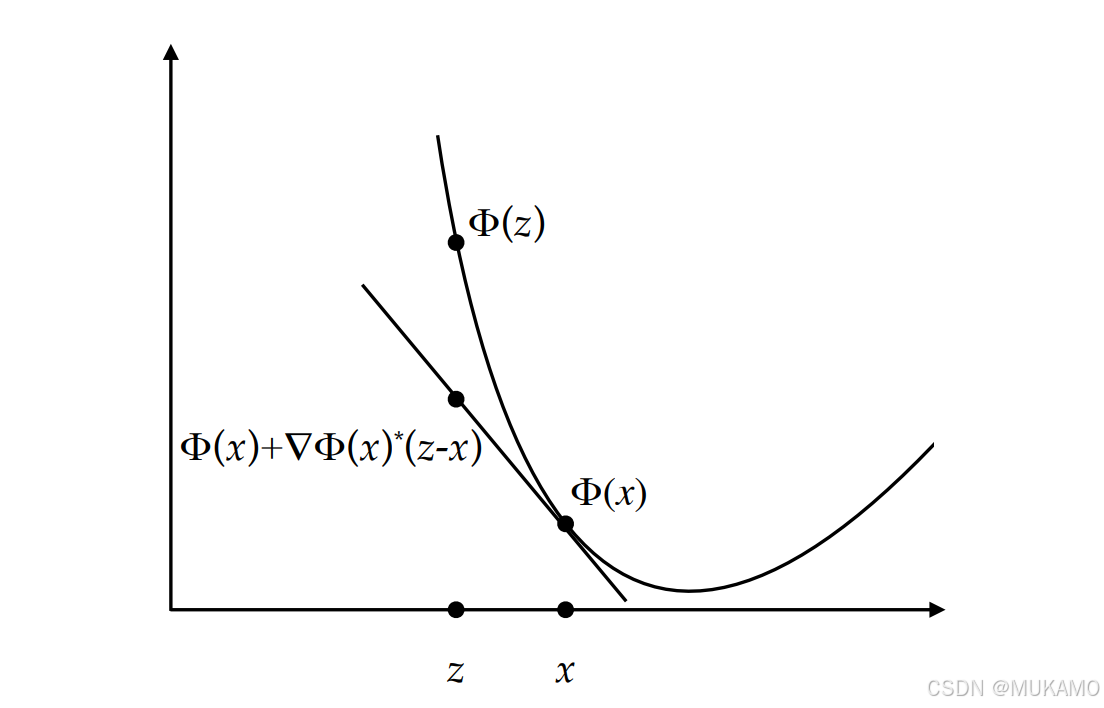
凸函数的切超平面总是位于函数图形的下方。
命题 6:函数图像的切平面
设
Φ
:
R
d
→
R
\Phi : \mathbb{R}^d \rightarrow \mathbb{R}
Φ:Rd→R 是一个可微凸函数。那么对于任意的
u
u
u 和
v
v
v,我们有
Φ
(
u
)
≥
Φ
(
v
)
+
∇
Φ
(
v
)
T
(
u
−
v
)
\Phi(u) \geq \Phi(v) + \nabla \Phi(v)^T (u - v)
Φ(u)≥Φ(v)+∇Φ(v)T(u−v)
3.凸函数的构造法则
在高维空间中判断一个函数是否凸可能比较复杂,但以下五条基本规则可以帮助我们从简单函数构造出凸函数。在机器学习领域,几乎所有的凸代价函数都是依据这些规则构建的。
- 所有范数都是凸的:这一点直接由三角不等式得出。
- 凸函数的非负缩放:如果 Φ \Phi Φ 是凸函数,且 α ≥ 0 \alpha \geq 0 α≥0,则 α Φ \alpha \Phi αΦ 也是凸的。
- 凸函数的和:如果 Φ \Phi Φ 和 Ψ \Psi Ψ 都是凸函数,那么它们的和 Φ + Ψ \Phi + \Psi Φ+Ψ 也是凸的。
- 凸函数的最大值:如果 Φ \Phi Φ 和 Ψ \Psi Ψ 都是凸函数,那么 h ( w ) = max { Φ ( w ) , Ψ ( w ) } h(w) = \max\{\Phi(w), \Psi(w)\} h(w)=max{Φ(w),Ψ(w)} 也是凸的。
- 线性变换后的凸函数:如果 Φ \Phi Φ 是凸函数, A A A 是矩阵, b b b 是向量,那么 h ( w ) = Φ ( A w + b ) h(w) = \Phi(Aw + b) h(w)=Φ(Aw+b) 也是凸的。
这些属性都可以通过凸函数的定义来验证。例如,第四条规则可能是列表中最不明显的。假设我们有两个点
w
1
w_1
w1 和
w
2
w_2
w2,以及
α
∈
[
0
,
1
]
\alpha \in [0, 1]
α∈[0,1]。不妨假设
Φ
(
(
1
−
α
)
w
1
+
α
w
2
)
≥
Ψ
(
(
1
−
α
)
w
1
+
α
w
2
)
\Phi((1 - \alpha)w_1 + \alpha w_2) \geq \Psi((1 - \alpha)w_1 + \alpha w_2)
Φ((1−α)w1+αw2)≥Ψ((1−α)w1+αw2),则有:
h
(
(
1
−
α
)
w
1
+
α
w
2
)
=
max
{
Φ
(
(
1
−
α
)
w
1
+
α
w
2
)
,
Ψ
(
(
1
−
α
)
w
1
+
α
w
2
)
}
h((1 - \alpha)w_1 + \alpha w_2) =\\ \max\{\Phi((1 - \alpha)w_1 + \alpha w_2), \Psi((1 - \alpha)w_1 + \alpha w_2)\}
h((1−α)w1+αw2)=max{Φ((1−α)w1+αw2),Ψ((1−α)w1+αw2)}
=
Φ
(
(
1
−
α
)
w
1
+
α
w
2
)
= \Phi((1 - \alpha)w_1 + \alpha w_2)
=Φ((1−α)w1+αw2)
≤
(
1
−
α
)
Φ
(
w
1
)
+
α
Φ
(
w
2
)
\leq (1 - \alpha)\Phi(w_1) + \alpha \Phi(w_2)
≤(1−α)Φ(w1)+αΦ(w2)
≤
(
1
−
α
)
max
{
Φ
(
w
1
)
,
Ψ
(
w
1
)
}
+
α
max
{
Φ
(
w
2
)
,
Ψ
(
w
2
)
}
\leq (1 - \alpha) \max\{\Phi(w_1), \Psi(w_1)\} + \alpha \max\{\Phi(w_2), \Psi(w_2)\}
≤(1−α)max{Φ(w1),Ψ(w1)}+αmax{Φ(w2),Ψ(w2)}
=
(
1
−
α
)
h
(
w
1
)
+
α
h
(
w
2
)
= (1 - \alpha)h(w_1) + \alpha h(w_2)
=(1−α)h(w1)+αh(w2)
这里的第一级不等式是因为 Φ \Phi Φ 是凸的。其他部分都是根据 h h h 是 Φ \Phi Φ 和 Ψ \Psi Ψ 的最大值这一定义得出的。读者应将其他四个断言作为练习进行验证。
另一个有益的练习是使用这五条基本规则以及一维函数 f ( x ) = m x + b f(x) = mx + b f(x)=mx+b 对任何标量 m m m 和 b b b 都是凸的事实,来验证下一节中支持向量机(SVM)的代价函数是凸的。
4.经验风险最小化的应用
在决策理论问题的研究中,我们关注了用来统计错误的零一损失函数:
loss
(
y
b
,
y
)
=
1
{
y
y
b
<
0
}
\text{loss}(y_b, y) = \mathbb{1}_{\{y y_b < 0\}}
loss(yb,y)=1{yyb<0}
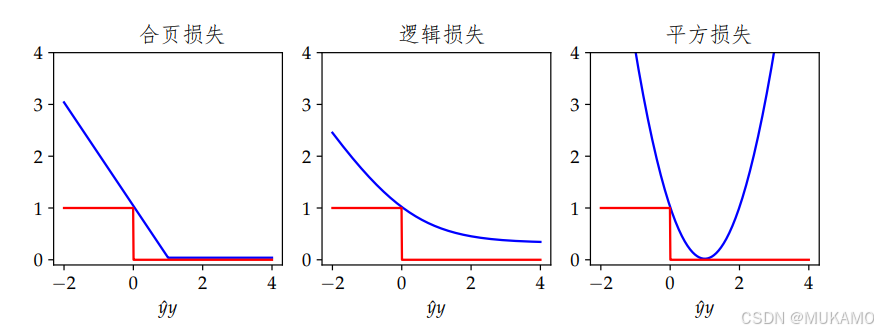
然而,这种损失函数对于梯度方法并不适用,因为它的梯度几乎在所有地方都为零。正如我们在监督学习章节中所讨论的,机器学习实践通常会转向寻找易于优化的替代损失函数。本文将回顾三种常用的选择,这些选择均为凸损失函数,每种选择都衍生出了独特的优化问题,这些问题本身都值得深入研究。
4.1.支持向量机(SVM)
考虑支持向量机分类的经典问题。我们得到了
(
x
i
,
y
i
)
(x_i, y_i)
(xi,yi) 的配对数据,其中
x
i
∈
R
d
x_i \in \mathbb{R}^d
xi∈Rd 且
y
i
∈
{
−
1
,
1
}
y_i \in \{-1, 1\}
yi∈{−1,1},对于
i
=
1
,
…
,
n
i = 1, \ldots, n
i=1,…,n(注意,现在的
y
y
y 标签使用
{
−
1
,
1
}
\{-1, 1\}
{−1,1} 而非
{
0
,
1
}
\{0, 1\}
{0,1})。我们的目标是找到一个向量
w
∈
R
d
w \in \mathbb{R}^d
w∈Rd 来满足以下条件:
w
T
x
i
>
0
当
y
i
=
1
w^T x_i > 0 \quad \text{当} \quad y_i = 1
wTxi>0当yi=1
w
T
x
i
<
0
当
y
i
=
−
1
w^T x_i < 0 \quad \text{当} \quad y_i = -1
wTxi<0当yi=−1
这样的
w
w
w 定义了一个半空间,我们认为所有正样本都位于这个半空间的一侧,而负样本位于另一侧。
我们不仅能够精确地对这些点进行分类,还可以允许一定的误差空间。对于那些没有被明确分类的点,我们可以引入一个罚项
1
−
y
i
w
T
x
i
1 - y_i w^T x_i
1−yiwTxi。这激发了我们使用之前遇到的铰链损失函数,并引出了支持向量机的目标函数:
min
w
∑
i
=
1
n
max
{
1
−
y
i
w
T
x
i
,
0
}
\min_{w} \sum_{i=1}^{n} \max\{1 - y_i w^T x_i, 0\}
wmini=1∑nmax{1−yiwTxi,0}
定义函数
e
(
z
)
=
1
{
z
≤
1
}
e(z) = \mathbb{1}_{\{z \leq 1\}}
e(z)=1{z≤1},我们可以计算出SVM成本的梯度为:
−
∑
i
=
1
n
e
(
y
i
w
T
x
i
)
y
i
x
i
-\sum_{i=1}^{n} e(y_i w^T x_i) y_i x_i
−i=1∑ne(yiwTxi)yixi
因此,这个ERM问题的梯度下降迭代将遵循以下步骤:
w
t
+
1
=
w
t
+
α
∑
i
=
1
n
e
(
y
i
w
T
x
i
)
y
i
x
i
w_{t+1} = w_t + \alpha \sum_{i=1}^{n} e(y_i w^T x_i) y_i x_i
wt+1=wt+αi=1∑ne(yiwTxi)yixi
虽然这与感知机方法相似,但请注意,这还不是完全的感知机方法。计算一个梯度步骤的时间复杂度为
O
(
n
)
O(n)
O(n),因为我们需要对所有
n
n
n 个内积求和。我们将很快讨论具有恒定迭代复杂度的随机梯度方法,它将包含感知机算法。
4.2.Logistic回归
Logistic回归等同于使用以下损失函数:
loss
(
y
b
,
y
)
=
log
(
1
+
exp
(
−
y
y
b
)
)
\text{loss}(y_b, y) = \log (1 + \exp(-y y_b))
loss(yb,y)=log(1+exp(−yyb))
注意,尽管这个损失函数具有概率解释,但它也可以被看作是对计数零一损失的近似。
4.3.最小二乘分类
最小二乘分类使用以下损失函数:
loss
(
y
b
,
y
)
=
1
2
(
y
b
−
y
)
2
\text{loss}(y_b, y) = \frac{1}{2} (y_b - y)^2
loss(yb,y)=21(yb−y)2
这可能看起来是对计数损失的一个不寻常的近似,但在最小化总体风险时,它会导致最大后验(MAP)决策规则。回想一下,MAP规则选择的是在给定观察数据的条件下概率最高的标签。
为了更好地理解这些损失函数如何近似零一损失,我们可以将其可视化。通过去掉因子 1 2 \frac{1}{2} 21,我们可以确保平方损失函数是对零一损失的一个上界。
5. 二次函数的启示
二次函数作为可微分优化问题的典型案例,为算法设计提供了灵感。虽然并非所有从二次优化中获得的洞见都适用于更一般的函数,但迭代算法在处理二次函数时的动态特性中有一些关键的共同点。此外,二次函数是评估优化算法的一个良好试验场:如果一个方法在处理二次函数时表现不佳,它通常也无法很好地处理更复杂的非线性优化问题。值得注意的是,当使用线性函数和平方损失时,经验风险最小化(ERM)问题实际上就是一个二次优化问题,这使得这类问题在机器学习实践中非常相关。
5.1.一般形式的二次优化问题
二次优化问题一般形式如下:
Φ
(
w
)
=
1
2
w
T
Q
w
−
p
T
w
+
r
,
\Phi(w) = \frac{1}{2} w^T Q w - p^T w + r,
Φ(w)=21wTQw−pTw+r,
这里,
Q
Q
Q 是一个对称矩阵,
p
p
p 是一个向量,而
r
r
r 是一个常数。常数
r
r
r 仅影响函数的值,对梯度下降的动态没有影响。该函数的梯度为:
∇
Φ
(
w
)
=
Q
w
−
p
.
\nabla \Phi(w) = Q w - p.
∇Φ(w)=Qw−p.
函数
Φ
\Phi
Φ 的静止点是满足
Q
w
=
p
Q w = p
Qw=p 的
w
w
w。如果
Q
Q
Q 是满秩的,那么存在一个唯一的静止点。
对于二次函数,梯度下降算法遵循以下迭代步骤:
w
t
+
1
=
w
t
−
α
(
Q
w
t
−
p
)
w_{t+1} = w_t - \alpha (Qw_t - p)
wt+1=wt−α(Qwt−p)
如果我们令
w
∗
w^*
w∗ 是
Φ
\Phi
Φ 的任意一个静止点,我们可以将迭代重写为:
w
t
+
1
−
w
∗
=
(
I
−
α
Q
)
(
w
t
−
w
∗
)
.
w_{t+1} - w^* = (I - \alpha Q)(w_t - w^*).
wt+1−w∗=(I−αQ)(wt−w∗).
展开这个递归关系,我们可以得到梯度下降迭代的封闭形式公式:
w
t
−
w
∗
=
(
I
−
α
Q
)
t
(
w
0
−
w
∗
)
w_t - w^* = (I - \alpha Q)^t (w_0 - w^*)
wt−w∗=(I−αQ)t(w0−w∗)
这个表达式揭示了几种可能的结果。设
λ
1
≥
λ
2
≥
…
≥
λ
d
\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_d
λ1≥λ2≥…≥λd 为
Q
Q
Q 的特征值。因为
Q
Q
Q 是对称的,这些特征值都是实数。首先,假设
Q
Q
Q 有一个负的特征值
λ
d
<
0
\lambda_d < 0
λd<0,并且
v
v
v 是相应的特征向量,满足
Q
v
=
λ
d
v
Q v = \lambda_d v
Qv=λdv。那么:
$(I - \alpha Q)^t v = (1 + \alpha |\lambda_d|)^t v, $
随着
t
t
t 的增长,如果
α
>
0
\alpha > 0
α>0,则
1
+
α
∣
λ
d
∣
1 + \alpha |\lambda_d|
1+α∣λd∣ 大于 1,因此上式趋向于无穷大。这意味着如果
⟨
v
,
w
0
−
w
∗
⟩
≠
0
\langle v, w_0 - w^* \rangle \neq 0
⟨v,w0−w∗⟩=0,梯度下降将会发散。对于一个随机的初始点
w
0
w_0
w0,我们期望这个点积不为零,因此梯度下降几乎肯定无法从随机初始化状态收敛。
如果
Q
Q
Q 的所有特征值都是正数,那么选择
0
<
α
<
1
λ
1
0 < \alpha < \frac{1}{\lambda_1}
0<α<λ11 将确保对于所有
k
k
k,
0
≤
1
−
α
λ
k
<
1
0 \leq 1 - \alpha \lambda_k < 1
0≤1−αλk<1。在这种情况下,梯度方法将以指数速率迅速收敛到最优
w
∗
w^*
w∗:
∣
∣
w
t
+
1
−
w
∗
∣
∣
=
∣
∣
(
I
−
α
Q
)
(
w
t
−
w
∗
)
∣
∣
≤
∣
∣
I
−
α
Q
∣
∣
∣
∣
w
t
−
w
∗
∣
∣
≤
(
1
−
λ
d
λ
1
)
∣
∣
w
t
−
w
∗
∣
∣
||w_{t+1}-w_*||=||(I-\alpha Q)(w_t-w_*)||\leq\\ ||I-\alpha Q||||w_t-w_*||\leq\\ (1-\frac{\lambda_d}{\lambda_1})||w_t-w_*||
∣∣wt+1−w∗∣∣=∣∣(I−αQ)(wt−w∗)∣∣≤∣∣I−αQ∣∣∣∣wt−w∗∣∣≤(1−λ1λd)∣∣wt−w∗∣∣
当
Q
Q
Q 的所有特征值都是正数时,函数
Φ
\Phi
Φ 是强凸的。强凸函数是一类特殊的函数,对于这类函数,使用恒定步长的梯度下降算法可以从任何起始点以指数速率收敛。
λ
1
\lambda_1
λ1 和
λ
d
\lambda_d
λd 的比率决定了所有分量收敛到零的速度。定义
Q
Q
Q 的条件数为
κ
=
λ
1
λ
d
\kappa = \frac{\lambda_1}{\lambda_d}
κ=λdλ1,并将步长
α
\alpha
α 设置为
1
λ
1
\frac{1}{\lambda_1}
λ11,我们得到以下界限:
∣
∣
w
t
−
w
∗
∣
∣
≤
(
1
−
λ
−
1
)
t
∣
∣
w
0
−
w
∗
∣
∣
||w_t - w_*|| \leq (1 - \lambda^{-1})^t||w_0 - w_*||
∣∣wt−w∗∣∣≤(1−λ−1)t∣∣w0−w∗∣∣
这个速率反映了实际应用中的情况:当存在较小的奇异值时,梯度下降可能会在图中所示的区域内发生反弹和振荡。当
Q
Q
Q 的条件数较小时,梯度下降会迅速向最优解靠近。
最后,值得考虑的一个特殊情况是,当 Q Q Q 的所有特征值都是非负的,但其中一些为零时,函数 Φ \Phi Φ 是凸的,但不强凸。在这种情况下,无法保证以指数速率收敛到一个唯一点。特别是,将存在无限多的 Φ \Phi Φ 的全局最小化解。如果 w ∗ w^* w∗ 是全局最小化解,而 v v v 是任何满足 Q v = 0 Q v = 0 Qv=0 的向量,那么 w ∗ + v w^* + v w∗+v 也是一个全局最小化解。然而,在对应于正特征值的特征向量空间内,梯度下降仍然以指数速率收敛。对于一般凸函数,要完全理解梯度方法的动态,考虑参数空间的不同部分将是重要的。
6.随机梯度下降法
6.1.随机梯度下降的基本思想
在现代数据分析和机器学习领域,随机梯度下降算法(Stochastic Gradient Descent, SGD)已成为最受青睐的优化工具之一。这一算法历史悠久,被不同的研究群体在多个场合独立“发明”,并以“最小均方”、“反向传播”、“在线学习”以及“随机Kaczmarz方法”等不同名称为人所知。普遍认为,这一算法的原型最早由Robbins和Monro在1951年提出,他们使用这种方法解决了一个更具普遍性的问题。
让我们再次聚焦于我们的核心目标:最小化针对参数向量
w
\mathbf{w}
w 的经验风险。以线性分类问题为例,其中
w
\mathbf{w}
w 是一个
d
d
d 维向量,并且定义了如下的线性预测函数:
f
(
x
i
;
w
)
=
w
T
x
i
f(\mathbf{x}_i; \mathbf{w}) = \mathbf{w}^T \mathbf{x}_i
f(xi;w)=wTxi
随机梯度下降法的核心思想基于这样一个观察:总和的梯度等同于其各个部分梯度的总和。因此,每个单独的部分都为我们提供了关于如何优化整个总和的有用信息。在随机梯度下降法中,我们通过跟踪单个随机样本上计算的风险函数的梯度来最小化经验风险。这种方法的直观逻辑是,如果我们沿着预期的下降方向进行迭代,那么给足够的时间,我们应该能够接近最优解。
然而,实现这一目标并不像听起来那么简单。值得注意的是,即使总和的梯度为零,各个单独项的梯度可能并不为零。这意味着 w ∗ \mathbf{w}^* w∗(最优参数向量)不再是一个固定点,这增加了对算法行为分析的复杂性。尽管存在这些挑战,随机梯度下降法因其在处理大规模数据集时的高效性而广受欢迎,并在机器学习的不同应用中发挥着关键作用。
6.2.随机梯度下降法的应用示例
6.2.1.支持向量机的随机梯度下降法应用
随机梯度下降法可以应用于支持向量机(SVM)的损失函数优化。我们从初始参数向量
w
0
\mathbf{w}_0
w0 开始,在第
t
t
t 次迭代中随机选取数据点
(
x
i
,
y
i
)
(\mathbf{x}_i, y_i)
(xi,yi) 并根据以下规则更新参数向量:
w
t
+
1
=
w
t
+
η
y
i
x
i
1
{
y
i
w
t
T
x
i
≤
1
}
\mathbf{w}_{t+1} = \mathbf{w}_t + \eta y_i \mathbf{x}_i \mathbb{1}_{\{ y_i \mathbf{w}_t^T \mathbf{x}_i \leq 1 \}}
wt+1=wt+ηyixi1{yiwtTxi≤1}
如果条件
y
i
w
t
T
x
i
>
1
y_i \mathbf{w}_t^T \mathbf{x}_i > 1
yiwtTxi>1 不满足,则保持
w
t
+
1
=
w
t
\mathbf{w}_{t+1} = \mathbf{w}_t
wt+1=wt 不变。这种方法实际上是Rosenblatt提出的感知机算法的等价形式,用于最小化带有铰链损失的经验风险。
6.2.2.随机梯度下降法计算均值
接下来,我们通过一个简单的例子来演示随机梯度下降法。考虑以下函数:
1
2
n
∑
i
=
1
n
(
w
−
y
i
)
2
\frac{1}{2n} \sum_{i=1}^{n} (\mathbf{w} - y_i)^2
2n1i=1∑n(w−yi)2
其中
y
1
,
…
,
y
n
y_1, \ldots, y_n
y1,…,yn 是已知的标量值,这代表了一个特征值全为1的简单分类问题。每个增量项的梯度为:
∇
loss
(
f
(
x
i
;
w
)
,
y
)
=
w
−
y
i
\nabla \text{loss}(f(\mathbf{x}_i; \mathbf{w}), y) = \mathbf{w} - y_i
∇loss(f(xi;w),y)=w−yi
假设随机样本按顺序
{
1
,
2
,
3
,
…
}
\{1, 2, 3, \ldots\}
{1,2,3,…} 到达,初始参数
w
1
=
0
w_1 = 0
w1=0,步长
α
k
=
1
/
k
\alpha_k = 1/k
αk=1/k。我们可以推导出参数更新公式:
w
k
+
1
=
(
1
−
1
k
+
1
)
w
k
+
1
k
+
1
y
k
=
1
k
+
1
∑
i
=
1
k
+
1
y
i
w_{k+1} = \left(1 - \frac{1}{k+1}\right) w_k + \frac{1}{k+1} y_k = \frac{1}{k+1} \sum_{i=1}^{k+1} y_i
wk+1=(1−k+11)wk+k+11yk=k+11i=1∑k+1yi
经过
n
n
n 步迭代后,
w
n
w_n
wn 即为
y
i
y_i
yi 的均值,这可以通过梯度验证为经验风险最小化问题的解。Robbins和Monro提出的1/k步长在此例中表明,随机梯度下降法可以被视为计算移动平均值的过程。
在更现实的随机设置中,数据可能以任意顺序到达。考虑函数:
R
(
w
)
=
1
2
E
[
(
w
−
Y
)
2
]
R(\mathbf{w}) = \frac{1}{2} \mathbb{E}[(\mathbf{w} - Y)^2]
R(w)=21E[(w−Y)2]
其中
Y
Y
Y 是均值为
μ
\mu
μ,方差为
σ
2
\sigma^2
σ2 的随机变量。如果在每一步使用独立同分布的样本
Y
i
Y_i
Yi 进行
k
k
k 次迭代,则有:
w
k
=
1
k
∑
i
=
1
k
Y
i
\mathbf{w}_k = \frac{1}{k} \sum_{i=1}^{k} Y_i
wk=k1i=1∑kYi
相关的成本为:
R
(
w
k
)
=
1
2
E
[
(
1
k
∑
i
=
1
k
Y
i
−
Y
)
2
]
=
σ
2
2
k
+
1
2
σ
2
R(\mathbf{w}_k) = \frac{1}{2} \mathbb{E}\left[\left(\frac{1}{k} \sum_{i=1}^{k} Y_i - Y\right)^2\right] = \frac{\sigma^2}{2k} + \frac{1}{2} \sigma^2
R(wk)=21E
(k1i=1∑kYi−Y)2
=2kσ2+21σ2
与可实现的最小风险
R
∗
R^*
R∗ 比较,我们发现最小化解
w
∗
=
μ
\mathbf{w}^* = \mu
w∗=μ,其成本为:
R
∗
=
R
(
w
∗
)
=
1
2
σ
2
R^* = R(\mathbf{w}^*) = \frac{1}{2} \sigma^2
R∗=R(w∗)=21σ2
经过
n
n
n 次迭代,预期的最优性差距为:
E
[
R
(
w
n
)
−
R
∗
]
=
σ
2
2
n
\mathbb{E}[R(\mathbf{w}_n) - R^*] = \frac{\sigma^2}{2n}
E[R(wn)−R∗]=2nσ2
这表明,即使在随机梯度下降法中,我们也能达到与考虑所有数据的解决方案一样好的结果。
6.2.3.二次函数的随机最小化
考虑一个更一般的随机梯度下降版本,它遵循梯度加上一些无偏噪声。设
Φ
(
w
)
\Phi(\mathbf{w})
Φ(w) 是我们要最小化的目标函数,迭代方向为
∇
Φ
(
w
)
+
ν
\nabla \Phi(\mathbf{w}) + \nu
∇Φ(w)+ν,其中
ν
\nu
ν 是均值为零且
E
[
∥
ν
∥
2
]
=
σ
2
\mathbb{E}[\|\nu\|^2] = \sigma^2
E[∥ν∥2]=σ2 的随机向量。特别地,如果
Φ
(
w
)
\Phi(\mathbf{w})
Φ(w) 是一个二次函数:
Φ
(
w
)
=
1
2
w
T
Q
w
−
p
T
w
+
r
\Phi(\mathbf{w}) = \frac{1}{2} \mathbf{w}^T Q \mathbf{w} - \mathbf{p}^T \mathbf{w} + r
Φ(w)=21wTQw−pTw+r
其中
Q
Q
Q 是正定矩阵,具有最大特征值
λ
1
\lambda_1
λ1 和最小特征值
λ
d
>
0
\lambda_d > 0
λd>0。迭代过程可以表示为:
w
t
+
1
=
w
t
−
α
(
Q
w
t
−
p
+
ν
t
)
\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha(Q \mathbf{w}_t - \mathbf{p} + \nu_t)
wt+1=wt−α(Qwt−p+νt)
假设
α
<
1
λ
1
\alpha < \frac{1}{\lambda_1}
α<λ11,我们可以推导出:
E
[
∥
w
t
−
w
∗
∥
2
]
≤
(
1
−
α
λ
d
)
2
t
∥
w
0
−
w
∗
∥
2
+
α
σ
2
λ
d
\mathbb{E}[\|\mathbf{w}_t - \mathbf{w}^*\|^2] \leq (1 - \alpha \lambda_d)^{2t} \|\mathbf{w}_0 - \mathbf{w}^*\|^2 + \frac{\alpha \sigma^2}{\lambda_d}
E[∥wt−w∗∥2]≤(1−αλd)2t∥w0−w∗∥2+λdασ2
这表明梯度下降法以指数速率快速收敛到最优解周围的某个区域内。步长
α
\alpha
α 的选择是关键,较小的
α
\alpha
α 使收敛更接近最优解,但收敛速率会变慢。这种权衡是设计随机梯度下降步长选择规则的动机之一,通常初始步长较大,随着算法的进行逐渐减小。
6.3.提升随机梯度下降性能的策略
在本节中,我们将探讨一系列关键的工程技术技巧,这些技巧对于优化随机梯度下降(SGD)的性能至关重要。每位涉足机器学习的实践者都应掌握以下这些高效的策略。
6.3.1.数据洗牌(Shuffling)
虽然在理论上,随机梯度方法是通过有放回地抽样来计算每个梯度,但在实践中,通过随机排列数据点的顺序并按照这一顺序执行SGD,往往能够获得更佳的性能。这种技术被称为“洗牌”。洗牌技术可以有效避免在数据高度相关时出现的病态行为。近期的研究表明,洗牌方法在理论上比无放回抽样更优。尽管无放回抽样的论证过程更为复杂,但SGD的最优抽样方法仍是当前研究中的一个活跃领域。
6.3.2.步长选择(Step Size Selection)
在SGD中,步长的选择一直是一个备受争议的话题。在处理简单的一维经验风险最小化(ERM)问题时,我们发现采用逐渐减小的步长 (1/k) 能够取得良好的效果。然而,在多数情况下,一个有效的经验规则是选择一个足够大的步长,以避免算法发散,同时确保模型性能有显著提升。通过从较大的初始步长逐步减小到更小的步长,我们可以更精确地逼近最优解。
6.3.3.步长衰减(Step Decay)
步长的调整通常在固定次数的数据遍历后进行,每次遍历整个数据集称为一个“纪元”(epoch)。在一个纪元中,执行一定数量的迭代后,会决定是否调整步长。一个常见的策略是,在固定数量的迭代 T T T 后,将步长乘以一个常数衰减因子 γ \gamma γ。例如,如果我们的初始步长是 α \alpha α,在第 k k k 个纪元,步长将调整为 α γ k − 1 \alpha \gamma^{k-1} αγk−1。这种方法通常比逐渐减小步长的规则更为稳健。在选择衰减因子 γ \gamma γ 时,一个合理的经验值范围是0.8到0.9之间。
6.3.4.小批量处理(Minibatching)
为了利用并行计算的优势,一种称为“小批量处理”的技术被广泛应用。小批量处理是通过计算多个随机梯度的平均值来近似真实梯度。假设在每次迭代中,我们抽取一个包含 (m) 个数据点的小批量
batch
k
\text{batch}_k
batchk,更新规则变为:
w
k
+
1
=
w
k
−
α
k
1
m
∑
j
∈
batch
k
∇
w
loss
(
f
(
x
j
;
w
k
)
,
y
j
)
\mathbf{w}_{k+1} = \mathbf{w}_k - \alpha_k \frac{1}{m} \sum_{j \in \text{batch}_k} \nabla_{\mathbf{w}} \text{loss}(f(\mathbf{x}_j; \mathbf{w}_k), y_j)
wk+1=wk−αkm1j∈batchk∑∇wloss(f(xj;wk),yj)
小批量处理可以降低随机梯度估计的方差,从而提供一个更优的下降方向。当然,小批量的大小与总计算时间之间需要权衡,这通常需要根据具体情况进行调整。
6.3.5.动量(Momentum)
最后,我们注意到,随机梯度下降可以结合动量进行优化。动量方法通过将当前梯度方向与之前的步伐相结合,以此来平滑更新过程。如果之前的权重更新是有效的,我们可能希望继续沿此方向前进。算法的迭代定义为:
w
k
+
1
=
w
k
−
α
k
g
k
(
w
)
+
β
(
w
k
−
w
k
−
1
)
\mathbf{w}_{k+1} = \mathbf{w}_k - \alpha_k g_k(\mathbf{w}) + \beta (\mathbf{w}_k - \mathbf{w}_{k-1})
wk+1=wk−αkgk(w)+β(wk−wk−1)
其中
g
k
g_k
gk 表示随机梯度。在实践中,动量方法非常成功,
β
\beta
β 的典型选择范围在0.8到0.95之间。动量可以显著加速收敛过程,应被视为实现SGD时的一个可选项。
6.4.随机梯度下降(SGD)快速指引
对于刚接触随机梯度下降的新手来说,面对众多的设计选择可能会感到不知所措。这里有一些简单的经验规则可以帮助你快速上手:
- 选择大批量尺寸:根据你计算机的内存(RAM),尽可能选择大的小批量(minibatch)尺寸。
- 设置动量参数:将动量参数设置为0或0.9,具体取决于你的选择。
- 确定合适的步长:通过试验和调整,找到一个恒定的步长值,使得SGD过程不会发散。这一步需要一定的尝试,但你的步长值只需要在这个数量级内正确即可。
- 稳定运行SGD:使用确定的恒定步长值运行SGD,直到经验风险(empirical risk)达到稳定状态。
- 减少步长:当经验风险稳定后,将步长减少一个固定的比例(例如,减少到原来的1/10)。
- 重复过程直至收敛:继续执行步骤4和5,直到模型收敛到满意的解。
虽然这种方法可能不是在所有情况下都最优的策略,但它提供了一个非常实用的起点,并且对于我们遇到的大多数应用场景(大约90%)来说已经足够有效。遵循这些简单的规则,你可以迅速开始你的SGD之旅,并逐步优化你的模型性能。
7. 随机梯度方法的理论分析
7.1.随机梯度方法迭代
在深入研究随机梯度方法之前,我们首先建立一些分析的约定。我们假设目标是最小化一个定义在
R
d
\mathbb{R}^d
Rd 上的凸函数
R
R
R。设
w
∗
\mathbf{w}^*
w∗ 为
R
R
R 的任意最优解。在每次迭代中,我们可以访问到一个随机函数
g
(
w
;
ξ
)
g(\mathbf{w}; \xi)
g(w;ξ),满足
E
[
ξ
]
[
g
(
w
;
ξ
)
]
=
∇
R
(
w
)
.
\mathbb{E}[\xi][g(\mathbf{w}; \xi)] = \nabla R(\mathbf{w}).
E[ξ][g(w;ξ)]=∇R(w).
这里,
ξ
\xi
ξ 是一个随机变量,决定了我们梯度方向的外观。我们还假设随机梯度是有界的,即存在非负常数
B
B
B 使得
∥
g
(
w
;
ξ
)
∥
≤
B
.
\|g(\mathbf{w}; \xi)\| \leq B.
∥g(w;ξ)∥≤B.
我们研究的随机梯度迭代公式为:
w
t
+
1
=
w
t
−
α
t
g
(
w
t
;
ξ
t
)
.
\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha_t g(\mathbf{w}_t; \xi_t).
wt+1=wt−αtg(wt;ξt).
我们假设
{
ξ
j
}
\{\xi_j\}
{ξj} 序列是从一个固定分布中独立同分布选取的。
我们从展开到最优解的距离开始分析:
∥
w
t
+
1
−
w
∗
∥
2
=
∥
w
t
−
α
t
g
(
w
t
;
ξ
t
)
−
w
∗
∥
2
=
∥
w
t
−
w
∗
∥
2
−
2
α
t
⟨
g
(
w
t
;
ξ
t
)
,
w
t
−
w
∗
⟩
+
α
t
2
∥
g
(
w
t
;
ξ
t
)
∥
2
.
\|\mathbf{w}_{t+1} - \mathbf{w}^*\|^2 = \|\mathbf{w}_t - \alpha_t g(\mathbf{w}_t; \xi_t) - \mathbf{w}^*\|^2 = \\\|\mathbf{w}_t - \mathbf{w}^*\|^2 - 2\alpha_t \langle g(\mathbf{w}_t; \xi_t), \mathbf{w}_t - \mathbf{w}^* \rangle + \alpha_t^2 \|g(\mathbf{w}_t; \xi_t)\|^2.
∥wt+1−w∗∥2=∥wt−αtg(wt;ξt)−w∗∥2=∥wt−w∗∥2−2αt⟨g(wt;ξt),wt−w∗⟩+αt2∥g(wt;ξt)∥2.
我们将分别处理这个展开的每一项。首先,应用期望的迭代法则,我们有:
E
[
ξ
t
]
[
⟨
g
(
w
t
;
ξ
t
)
,
w
t
−
w
∗
⟩
]
=
E
[
⟨
∇
R
(
w
t
)
,
w
t
−
w
∗
⟩
]
.
\mathbb{E}[\xi_t][\langle g(\mathbf{w}_t; \xi_t), \mathbf{w}_t - \mathbf{w}^* \rangle] = \mathbb{E}[\langle \nabla R(\mathbf{w}_t), \mathbf{w}_t - \mathbf{w}^* \rangle].
E[ξt][⟨g(wt;ξt),wt−w∗⟩]=E[⟨∇R(wt),wt−w∗⟩].
这里使用了
ξ
t
\xi_t
ξt 独立于之前所有
ξ
i
\xi_i
ξi(因此
ξ
t
\xi_t
ξt 独立于
w
t
\mathbf{w}_t
wt)的事实。这意味着在迭代期望时,随机梯度可以替换为梯度。
最后一项可以用梯度有界的假设来限制:
E
[
∥
g
(
w
t
;
ξ
t
)
∥
2
]
≤
B
2
.
\mathbb{E}[\|g(\mathbf{w}_t; \xi_t)\|^2] \leq B^2.
E[∥g(wt;ξt)∥2]≤B2.
设
δ
t
:
=
E
[
∥
w
t
−
w
∗
∥
2
]
\delta_t := \mathbb{E}[\|\mathbf{w}_t - \mathbf{w}^*\|^2]
δt:=E[∥wt−w∗∥2],我们得到:
δ
t
+
1
≤
δ
t
−
2
α
t
E
[
⟨
∇
R
(
w
t
)
,
w
t
−
w
∗
⟩
]
+
α
t
2
B
2
.
\delta_{t+1} \leq \delta_t - 2\alpha_t \mathbb{E}[\langle \nabla R(\mathbf{w}_t), \mathbf{w}_t - \mathbf{w}^* \rangle] + \alpha_t^2 B^2.
δt+1≤δt−2αtE[⟨∇R(wt),wt−w∗⟩]+αt2B2.
现在,设
λ
t
=
∑
j
=
0
t
α
j
\lambda_t = \sum_{j=0}^{t} \alpha_j
λt=∑j=0tαj 表示到第
t
t
t 次迭代为止所有步长的总和。定义按步长加权的迭代平均值为:
w
ˉ
t
=
1
λ
t
∑
j
=
0
t
α
j
w
j
.
\bar{\mathbf{w}}_t = \frac{1}{\lambda_t} \sum_{j=0}^{t} \alpha_j \mathbf{w}_j.
wˉt=λt1j=0∑tαjwj.
我们将分析
R
(
w
ˉ
t
)
R(\bar{\mathbf{w}}_t)
R(wˉt) 与最优解的偏差。
设 ρ 0 = ∥ w 0 − w ∗ ∥ \rho_0 = \|\mathbf{w}_0 - \mathbf{w}^*\| ρ0=∥w0−w∗∥ 为初始距离至最优解。 ρ 0 \rho_0 ρ0 未必是随机变量。
继续分析,我们展开以下表达式:
E
[
R
(
w
ˉ
T
)
−
R
(
w
∗
)
]
≤
1
λ
T
∑
t
=
0
T
α
t
(
R
(
w
t
)
−
R
(
w
∗
)
)
\mathbb{E}[R(\bar{\mathbf{w}}_T) - R(\mathbf{w}^*)] \leq \frac{1}{\lambda_T} \sum_{t=0}^{T} \alpha_t (R(\mathbf{w}_t) - R(\mathbf{w}^*))
E[R(wˉT)−R(w∗)]≤λT1t=0∑Tαt(R(wt)−R(w∗))
≤
1
λ
T
∑
t
=
0
T
α
t
E
[
⟨
∇
R
(
w
t
)
,
w
t
−
w
∗
⟩
]
\leq \frac{1}{\lambda_T} \sum_{t=0}^{T} \alpha_t \mathbb{E}[\langle \nabla R(\mathbf{w}_t), \mathbf{w}_t - \mathbf{w}^* \rangle]
≤λT1t=0∑TαtE[⟨∇R(wt),wt−w∗⟩]
≤
1
2
λ
T
∑
t
=
0
T
(
δ
t
−
δ
t
+
1
)
+
1
2
∑
t
=
0
T
α
t
2
B
2
\leq \frac{1}{2\lambda_T} \sum_{t=0}^{T} (\delta_t - \delta_{t+1}) + \frac{1}{2} \sum_{t=0}^{T} \alpha_t^2 B^2
≤2λT1t=0∑T(δt−δt+1)+21t=0∑Tαt2B2
=
ρ
0
2
+
B
2
1
λ
T
∑
t
=
0
T
α
t
2
.
= \rho_0^2 + B^2 \frac{1}{\lambda_T} \sum_{t=0}^{T} \alpha_t^2.
=ρ02+B2λT1t=0∑Tαt2.
这里的第一级不等式是因为 R R R 是凸的(线段位于函数上方,即 R ( w ∗ ) ≥ R ( w t ) + ⟨ ∇ R ( w t ) , w ∗ − w t ⟩ R(\mathbf{w}^*) \geq R(\mathbf{w}_t) + \langle \nabla R(\mathbf{w}_t), \mathbf{w}^* - \mathbf{w}_t \rangle R(w∗)≥R(wt)+⟨∇R(wt),w∗−wt⟩)。第二级不等式利用了梯度定义了 R R R 的切平面并且始终位于 R R R 的图形下方,第三级不等式使用了我们上面推导出的 δ t \delta_t δt 的递归关系。
通过这种分析,我们得到了一些有意义的结果。
7.2. 定理3:随机梯度方法的收敛性分析
考虑在凸函数
R
R
R 上应用随机梯度方法(SGM),该函数具有最小值
R
∗
R^*
R∗。我们进行
T
T
T 步迭代,步长为
α
\alpha
α。定义最优步长为:
α
opt
=
ρ
0
B
T
\alpha_{\text{opt}} = \frac{\rho_0}{B \sqrt{T}}
αopt=BTρ0
这里,
ρ
0
\rho_0
ρ0 是初始距离至最优解,
B
B
B 是随机梯度的上界。
接着,定义步长比
θ
\theta
θ 为当前步长
α
\alpha
α 与最优步长
α
opt
\alpha_{\text{opt}}
αopt 的比值:
θ
=
α
α
opt
\theta = \frac{\alpha}{\alpha_{\text{opt}}}
θ=αoptα
根据定理,我们得到关于次优解的界限:
E
[
R
(
w
ˉ
T
)
−
R
∗
]
≤
(
1
2
θ
+
1
2
θ
2
)
B
ρ
0
T
\mathbb{E}[R(\bar{\mathbf{w}}_T) - R^*] \leq \left(\frac{1}{2\theta} + \frac{1}{2\theta^2}\right) B\rho_0 \sqrt{T}
E[R(wˉT)−R∗]≤(2θ1+2θ21)Bρ0T
这个命题指出,选择非最优常数步长会导致线性误差。例如,如果我们选择的常数步长是最优步长的两倍或一半,我们可能需要最多两倍的迭代次数来达到相同的精度。最优步长可以通过最小化次优差距的上界来找到。虽然这里讨论的是常数步长,但其他类型的步长,比如递减步长,也可以选择。然而,在给定的上界条件下,常数步长是最优的选择。
7.3.风险最小化的含义
首先,考虑经验风险最小化。假设我们最小化一个凸损失函数,寻找一个线性预测器,并假设存在一个经验风险为零的模型。设
C
C
C 为损失函数梯度的最大值,
D
D
D 为任意样本
x
i
\mathbf{x}_i
xi 的范数的最大值,
ρ
\rho
ρ 为使得
R
S
[
w
]
=
0
R_S[\mathbf{w}] = 0
RS[w]=0 的
w
\mathbf{w}
w 的最小范数。我们得到经验风险的界限:
E
[
R
S
[
w
ˉ
T
]
]
≤
C
D
ρ
T
\mathbb{E}[R_S[\bar{\mathbf{w}}_T]] \leq \frac{CD\rho}{\sqrt{T}}
E[RS[wˉT]]≤TCDρ
这表明,适当选择步长后,随机梯度方法以 1 / T 1/\sqrt{T} 1/T 的速率收敛,这与在一维均值计算问题中观察到的收敛速率相同。随机性迫使我们以 1 / T 1/\sqrt{T} 1/T 的速率缓慢收敛,但高维度并未改变这一速率。
其次,如果我们只对样本进行一次精确操作,并且假设数据是独立同分布的(i.i.d.),我们可以将随机梯度方法视为最小化总体风险而非经验风险。在相同的符号下,我们得到总体风险的界限:
E
[
R
[
w
ˉ
T
]
]
−
R
∗
≤
C
D
ρ
T
\mathbb{E}[R[\bar{\mathbf{w}}_T]] - R^* \leq \frac{CD\rho}{\sqrt{T}}
E[R[wˉT]]−R∗≤TCDρ
随机梯度的分析为我们提供了本书的第二个泛化界限。它揭示了通过在固定数量 T T T 的数据点上优化,我们可以得到一个在新数据上具有低成本的解决方案。
8. 隐含的凸性:非凸问题中的全局优化
我们一直专注于凸优化问题,并展示了梯度下降法如何以适度的计算资源找到全局最小值。然而,对于非凸问题,由于其普遍性,通常很难提供有用的保证。尽管如此,经验风险最小化(ERM)作为一种特殊的优化问题,其结构允许非凸性以一种优雅的方式存在。
8.1. ERM问题的隐含凸性
ERM问题中存在一种“隐含的凸性”,这表明即使我们无法精确分析模型的收敛位置,预测仍然会收敛到全局最优解。当模型过度参数化或非凸时,这种洞见尤其有用。
假设我们有一个损失函数,在
y
b
=
y
y_b = y
yb=y 时为零,其他情况下非负。我们有一个一般参数化的函数类
{
f
(
x
;
w
)
:
w
∈
R
d
}
\{ f(x; w): w \in \mathbb{R}^d \}
{f(x;w):w∈Rd},目标是找到最小化经验风险的参数
w
w
w。经验风险
R
S
[
w
]
R_S[w]
RS[w] 定义为:
R
S
[
w
]
=
1
n
∑
i
=
1
n
loss
(
f
(
x
i
;
w
)
,
y
i
)
R_S[w] = \frac{1}{n} \sum_{i=1}^{n} \text{loss}(f(\mathbf{x}_i; w), y_i)
RS[w]=n1i=1∑nloss(f(xi;w),yi)
由于
loss
\text{loss}
loss 函数的下界为0,如果能找到一个解,使得对于所有
i
i
i 都有
f
(
x
i
;
w
)
=
y
i
f(\mathbf{x}_i; w) = y_i
f(xi;w)=yi,那么我们得到的将是全局最小值而非局部最小值。这是一个简单的观察,但有助于我们集中研究。如果在优化过程中所有预测
f
(
x
i
;
w
)
f(\mathbf{x}_i; w)
f(xi;w) 都收敛到
y
i
y_i
yi,我们就计算出了全局最小化解。本节中,我们专注于平方损失函数:
loss
(
f
(
x
i
;
w
)
,
y
i
)
=
1
2
(
f
(
x
i
;
w
)
−
y
i
)
2
\text{loss}(f(\mathbf{x}_i; w), y_i) = \frac{1}{2} (f(\mathbf{x}_i; w) - y_i)^2
loss(f(xi;w),yi)=21(f(xi;w)−yi)2
8.2.过度参数化线性模型的收敛性
考虑线性预测函数
f
(
x
;
w
)
=
w
T
x
f(\mathbf{x}; w) = \mathbf{w}^T \mathbf{x}
f(x;w)=wTx。定义数据矩阵
X
\mathbf{X}
X 和目标向量
y
\mathbf{y}
y,经验风险目标可以写为:
R
S
[
w
]
=
1
2
n
∥
X
w
−
y
∥
2
R_S[w] = \frac{1}{2n} \|\mathbf{Xw} - \mathbf{y}\|^2
RS[w]=2n1∥Xw−y∥2
梯度下降更新规则为:
w
t
+
1
=
w
t
−
α
X
T
(
X
w
t
−
y
)
\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \mathbf{X}^T (\mathbf{Xw}_t - \mathbf{y})
wt+1=wt−αXT(Xwt−y)
定义预测向量
y
b
t
\mathbf{y}_b^t
ybt,对于线性情况,预测
y
b
,
k
t
=
x
k
T
w
t
y_{b,k}^t = \mathbf{x}_k^T \mathbf{w}_t
yb,kt=xkTwt。预测的演变规则为:
y
b
t
+
1
=
y
b
t
−
α
X
X
T
(
y
b
t
−
y
)
\mathbf{y}_{b}^{t+1} = \mathbf{y}_b^t - \alpha \mathbf{X} \mathbf{X}^T (\mathbf{y}_b^t - \mathbf{y})
ybt+1=ybt−αXXT(ybt−y)
这类似于我们之前研究的强凸二次函数的梯度下降算法。只要
X
X
T
\mathbf{X} \mathbf{X}^T
XXT 是严格正定的,并且
α
\alpha
α 足够小,预测就会收敛到训练标签。
8.3.过度参数化的优势
在 d > n d > n d>n 的情况下,即模型过度参数化时, n × n n \times n n×n 矩阵 X X T \mathbf{X} \mathbf{X}^T XXT 有可能严格正定。使用足够小的常数步长 α \alpha α,预测以指数速率收敛。这与超定问题上梯度方法的行为形成对比,其中权重的收敛速率可能只是迭代计数器的逆多项式。在过度参数化的情况下,我们可以保证预测比权重本身收敛得更快。
预测的收敛速率由矩阵 X \mathbf{X} X 的特性决定。我们需要 X X T \mathbf{X} \mathbf{X}^T XXT 的特征值是正的,理想情况下,所有特征值的幅度相似。一个必要条件是维度 d d d 必须大于数据点的数量 n n n。过度参数化的模型不仅能够插值任何标签集,还能强制数据线性可分。此外,过度参数化通过改善数据矩阵的条件数,鼓励优化方法在更少的迭代中收敛。
过度参数化还可以帮助加速收敛。 X X T \mathbf{X} \mathbf{X}^T XXT 的特征值是 X \mathbf{X} X 的奇异值的平方。通过奇异值分解 X = U S V T \mathbf{X} = \mathbf{U} \mathbf{S} \mathbf{V}^T X=USVT,其中 S \mathbf{S} S 是奇异值的对角矩阵。为了改善矩阵的条件数,添加一个集中在具有小奇异值的奇异向量空间上的特征就足够了。虽然找到这样的特征并不总是显而易见的,但这为我们寻找新的、有信息量的特征提供了一个起点。
8.4.非凸模型的收敛性分析
本节探讨了非凸模型收敛性的理论扩展,尽管模型非凸,但通过巧妙的分析方法,我们仍能洞察其优化过程。
8.4.1.非凸模型的目标函数
考虑一个非线性模型
f
(
x
;
w
)
f(\mathbf{x}; \mathbf{w})
f(x;w),它在输入
x
\mathbf{x}
x 上产生
n
n
n 个预测
y
b
\mathbf{y}_b
yb,由权重
w
\mathbf{w}
w 参数化。我们的目标是最小化平方损失目标函数:
1
2
∥
f
(
x
;
w
)
−
y
∥
2
.
\frac{1}{2} \| f(\mathbf{x}; \mathbf{w}) - \mathbf{y} \|^2.
21∥f(x;w)−y∥2.
8.4.2.梯度下降法的应用
在权重上应用梯度下降法,可以得到迭代更新公式:
w
t
+
1
=
w
t
−
α
D
f
(
x
;
w
t
)
⊤
(
y
b
t
−
y
)
,
\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)^\top (\mathbf{y}_b^t - \mathbf{y}),
wt+1=wt−αDf(x;wt)⊤(ybt−y),
其中
y
b
t
=
f
(
x
;
w
t
)
\mathbf{y}_b^t = f(\mathbf{x}; \mathbf{w}_t)
ybt=f(x;wt),
D
f
\mathbf{D} f
Df 是预测相对于
w
\mathbf{w}
w 的雅可比矩阵,
α
\alpha
α 是学习率。
8.4.3.高阶导数与泰勒展开
雅可比矩阵
D
f
\mathbf{D} f
Df 是
d
×
n
d \times n
d×n 维的,包含了
f
(
x
;
w
)
f(\mathbf{x}; \mathbf{w})
f(x;w) 相对于
w
\mathbf{w}
w 的一阶导数。黑塞矩阵
H
(
w
)
\mathbf{H}(\mathbf{w})
H(w) 表示为
n
×
d
×
d
n \times d \times d
n×d×d 数组,包含了
f
(
x
;
w
)
f(\mathbf{x}; \mathbf{w})
f(x;w) 的二阶导数。根据泰勒定理,我们可以将
y
b
t
+
1
\mathbf{y}_{b}^{t+1}
ybt+1 展开为:
y
b
t
+
1
=
f
(
x
,
w
t
+
1
)
=
f
(
x
,
w
t
)
+
D
f
(
x
;
w
t
)
⊤
(
w
t
+
1
−
w
t
)
+
∫
0
1
H
(
w
t
+
s
(
w
t
+
1
−
w
t
)
)
(
w
t
+
1
−
w
t
)
d
s
.
\mathbf{y}_{b}^{t+1} = f(\mathbf{x}, \mathbf{w}_{t+1}) =\\ f(\mathbf{x}, \mathbf{w}_t) + \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)^\top (\mathbf{w}_{t+1} - \mathbf{w}_t) + \int_0^1 \mathbf{H}(\mathbf{w}_t + \\s(\mathbf{w}_{t+1} - \mathbf{w}_t))(\mathbf{w}_{t+1} - \mathbf{w}_t) \, ds.
ybt+1=f(x,wt+1)=f(x,wt)+Df(x;wt)⊤(wt+1−wt)+∫01H(wt+s(wt+1−wt))(wt+1−wt)ds.
8.4.4.预测的迭代更新
由于
w
t
\mathbf{w}_t
wt 是梯度下降的迭代结果,我们可以将预测
y
b
t
+
1
\mathbf{y}_{b}^{t+1}
ybt+1 写为:
y
b
t
+
1
=
y
b
t
−
α
D
f
(
x
;
w
t
)
⊤
D
f
(
x
;
w
t
)
(
y
b
t
−
y
)
+
α
e
t
,
\mathbf{y}_{b}^{t+1} = \mathbf{y}_b^t - \alpha \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)^\top \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)(\mathbf{y}_b^t - \mathbf{y}) + \alpha \mathbf{e}_t,
ybt+1=ybt−αDf(x;wt)⊤Df(x;wt)(ybt−y)+αet,
其中误差项
e
t
\mathbf{e}_t
et 定义为:
e
t
=
∫
0
1
H
(
w
t
+
s
(
w
t
+
1
−
w
t
)
)
(
D
f
(
x
;
w
t
)
(
y
b
t
−
y
)
,
D
f
(
x
;
w
t
)
(
y
b
t
−
y
)
)
d
s
.
\mathbf{e}_t = \int_0^1 \mathbf{H}(\mathbf{w}_t + s(\mathbf{w}_{t+1} - \mathbf{w}_t)) \\(\mathbf{D} f(\mathbf{x}; \mathbf{w}_t)(\mathbf{y}_b^t - \mathbf{y}), \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)(\mathbf{y}_b^t - \mathbf{y})) \, ds.
et=∫01H(wt+s(wt+1−wt))(Df(x;wt)(ybt−y),Df(x;wt)(ybt−y))ds.
8.4.5.预测的收敛性
从两边减去标签
y
\mathbf{y}
y 并重新排列项,我们得到预测的递归公式:
y
b
t
+
1
−
y
=
(
I
−
α
D
f
(
x
;
w
t
)
⊤
D
f
(
x
;
w
t
)
)
(
y
b
t
−
y
)
+
α
e
t
.
\mathbf{y}_{b}^{t+1} - \mathbf{y} = (I - \alpha \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)^\top \mathbf{D} f(\mathbf{x}; \mathbf{w}_t))(\mathbf{y}_b^t - \mathbf{y}) + \alpha \mathbf{e}_t.
ybt+1−y=(I−αDf(x;wt)⊤Df(x;wt))(ybt−y)+αet.
如果误差项 e t \mathbf{e}_t et 消失,这表明只要 D f ( x ; w t ) ⊤ D f ( x ; w t ) \mathbf{D} f(\mathbf{x}; \mathbf{w}_t)^\top \mathbf{D} f(\mathbf{x}; \mathbf{w}_t) Df(x;wt)⊤Df(x;wt) 的特征值严格为正,预测就会收敛到训练标签。当 e t \mathbf{e}_t et 足够小的时候,类似的动态也会发生。我们期望 e t \mathbf{e}_t et 不会太大,因为它是 y t \mathbf{y}_t yt 到 y \mathbf{y} y 距离的二次项,并且它乘以了可以被选择得足够小的步长 α \alpha α。
8.4.6.非凸性的挑战与应对
非凸性在这里并不特别具有破坏性。我们只需要确保雅可比矩阵大多数时间都具有满秩,并且我们的步长不要太大。如果参数的数量大于数据点的数量,那么这些雅可比矩阵就可能严格正定,只要我们设计得好。但如何确切保证雅可比矩阵表现良好呢?我们可以通过解包函数组合的梯度计算方式来推导出一些合理的基本规则。这些内容将在我们关于深度学习的章节中进一步讨论。
9. 正则化:优化与泛化的桥梁
9.1.正则化的基本概念
正则化是机器学习中一个关键的概念,它介于优化和泛化之间,为两者建立了联系。我们不仅会在讨论优化的章节中遇到正则化,也会在泛化章节中探讨它。在处理过度参数化的模型时,我们会面临一个挑战:存在无限多的模型能够达到零经验风险。面对这种情况,我们应该如何做出选择,我们应该倾向于哪一套权重呢?
要回答这个问题,我们需要回顾监督学习的目标不仅仅在于实现零训练误差,我们还关心模型在训练集之外数据上的表现。单纯的零损失并不能告诉我们有关训练集外数据的任何信息。例如,假设我们有两组数据
X
train
\mathbf{X}_{\text{train}}
Xtrain 和
X
test
\mathbf{X}_{\text{test}}
Xtest,其中
X
train
\mathbf{X}_{\text{train}}
Xtrain 的形状为
n
×
d
n \times d
n×d,
X
test
\mathbf{X}_{\text{test}}
Xtest 为
m
×
d
m \times d
m×d。设
y
train
\mathbf{y}_{\text{train}}
ytrain 为训练标签,设
q
\mathbf{q}
q 为一个
m
m
m 维的随机标签向量。如果
d
>
(
m
+
n
)
d > (m + n)
d>(m+n),我们可以找到权重
w
\mathbf{w}
w 使得:
[
X
train
X
test
]
w
=
[
y
train
q
]
\begin{bmatrix} \mathbf{X}_{\text{train}} \\ \mathbf{X}_{\text{test}} \end{bmatrix} \mathbf{w} = \begin{bmatrix} \mathbf{y}_{\text{train}} \\ \mathbf{q} \end{bmatrix}
[XtrainXtest]w=[ytrainq]
这意味着这些权重在训练集上会产生零误差,但在测试集上的误差不会比随机猜测更好。这显然不是我们期望的行为。
监督学习的主要挑战在于设计能够在新数据上表现良好的模型,同时保持低训练误差。解决这类问题的主要工具称为正则化。正则化是一个通用术语,指的是在有无限多解的问题中,通过引入偏差来选择解空间的一个较小子集。这是一个非常广泛的概念。
有时,正则化是显式的,因为我们在优化问题中有一个期望的解的特性,我们将其作为约束来实现。有时,正则化是隐式的,因为算法设计选择导致唯一解,尽管这个解的特性可能不是立即显而易见的。
在本章中,我们从隐式正则化转向显式正则化,从随机梯度下降开始。
9.2.通过优化实现的隐式正则化
再次考虑梯度下降或随机梯度下降的线性情况:
w
t
+
1
=
w
t
−
α
e
t
,
\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \mathbf{e}_t,
wt+1=wt−αet,
其中
e
t
\mathbf{e}_t
et 是当前预测的损失梯度。如果我们初始化
w
0
=
0
\mathbf{w}_0 = 0
w0=0,那么
w
t
\mathbf{w}_t
wt 总是在数据的张成空间内。这可以通过简单的归纳法看出。这已经表明,尽管一般权重位于高维空间,但SGD在最多
n
n
n 维的空间中搜索,其中
n
n
n 是数据点的数量。
现在假设我们有一个非负损失函数,它的偏导数 ∂ loss ( z , y ) ∂ z \frac{\partial \text{loss}(z,y)}{\partial z} ∂z∂loss(z,y) 当且仅当 y = z y = z y=z 时为零。这个条件由平方损失满足,但铰链损失和逻辑损失不满足。对于这样的损失,在最优解下,对于一些向量 v \mathbf{v} v 我们有:
- X w = y \mathbf{Xw} = \mathbf{y} Xw=y,因为我们的损失为零。
- w = X ⊤ v \mathbf{w} = \mathbf{X}^\top \mathbf{v} w=X⊤v,因为我们在数据的张成空间内。
在数据样本线性独立的温和假设下,我们可以将这些方程组合起来找到:
w
=
X
⊤
(
X
X
⊤
)
−
1
y
.
\mathbf{w} = \mathbf{X}^\top (\mathbf{X}\mathbf{X}^\top)^{-1} \mathbf{y}.
w=X⊤(XX⊤)−1y.
也就是说,当我们运行随机梯度下降时,我们收敛到一个非常特定的解。尽管我们在一个
n
n
n 维空间中搜索,我们收敛到这个空间中的唯一点。
这个特殊的 w \mathbf{w} w 是 X w = y \mathbf{Xw} = \mathbf{y} Xw=y 的最小欧几里得范数解。换句话说,在所有插值训练数据的线性预测函数中,SGD选择了具有最小欧几里得范数的解。
为了理解为什么这个解具有最小的范数,假设
w
b
=
X
⊤
α
+
v
\mathbf{w}_b = \mathbf{X}^\top \alpha + \mathbf{v}
wb=X⊤α+v 其中
v
\mathbf{v}
v 与所有
x
i
\mathbf{x}_i
xi 正交。那么我们有:
X
w
b
=
X
X
⊤
α
+
X
v
=
X
X
⊤
α
.
\mathbf{Xw}_b = \mathbf{X}\mathbf{X}^\top \alpha + \mathbf{Xv} = \mathbf{X}\mathbf{X}^\top \alpha.
Xwb=XX⊤α+Xv=XX⊤α.
这意味着
α
\alpha
α 完全确定,因此
w
b
=
X
⊤
(
X
X
⊤
)
−
1
y
+
v
\mathbf{w}_b = \mathbf{X}^\top (\mathbf{X}\mathbf{X}^\top)^{-1} \mathbf{y} + \mathbf{v}
wb=X⊤(XX⊤)−1y+v。
但现在:
∥
w
b
∥
2
=
∥
X
⊤
(
X
X
⊤
)
−
1
y
∥
2
+
∥
v
∥
2
.
\|\mathbf{w}_b\|^2 = \|\mathbf{X}^\top (\mathbf{X}\mathbf{X}^\top)^{-1} \mathbf{y}\|^2 + \|\mathbf{v}\|^2.
∥wb∥2=∥X⊤(XX⊤)−1y∥2+∥v∥2.
最小化右侧表明
v
\mathbf{v}
v 必须等于零。
现在我们转向展示这样的最小范数解具有重要的稳健性属性,这表明它们在新数据上表现良好。在下一章中,我们将证明在合理假设下,这些方法保证在新数据上表现良好。
9.3.边缘效应与模型稳定性
设想一个能够完美区分数据且无任何分类误差的线性预测器。回忆一下,此预测器的决策边界是一个超平面,定义为
B
=
{
z
:
w
⊤
z
=
0
}
B = \{z : \mathbf{w}^\top z = 0\}
B={z:w⊤z=0}。预测器的边缘(margin)是指决策边界到最近数据点的距离,可以用以下公式表示:
margin
(
w
)
=
min
i
dist
(
x
i
,
B
)
.
\text{margin}(\mathbf{w}) = \min_i \text{dist}(\mathbf{x}_i, B).
margin(w)=imindist(xi,B).
鉴于我们假设
w
\mathbf{w}
w 能够正确分类所有训练数据,边缘可以更简洁地表示为:
margin
(
w
)
=
min
i
y
i
w
⊤
x
i
∥
w
∥
.
\text{margin}(\mathbf{w}) = \min_i \frac{y_i \mathbf{w}^\top \mathbf{x}_i}{\|\mathbf{w}\|}.
margin(w)=imin∥w∥yiw⊤xi.
理想情况下,我们希望数据点远离决策边界,这样我们的预测器就有较大的边缘。这种期望背后的逻辑是:如果新数据与训练数据相似,并且决策边界远离训练数据,那么新数据点位于决策边界错误一侧的可能性就会降低。边缘还告诉我们 x i \mathbf{x}_i xi 可以承受多大的扰动而不会被错误分类,这是预测器对数据变化敏感度的一种度量。
接下来,我们将边缘的概念应用到上一节中描述的插值场景中。在假设我们通过插值标签满足
w
⊤
x
i
=
y
i
\mathbf{w}^\top \mathbf{x}_i = y_i
w⊤xi=yi 的情况下,边缘可以表示为:
margin
(
w
)
=
1
∥
w
∥
.
\text{margin}(\mathbf{w}) = \frac{1}{\|\mathbf{w}\|}.
margin(w)=∥w∥1.
如果我们想在最大化边缘的同时对数据进行插值,那么最佳选择是选取满足 X w = y \mathbf{Xw} = \mathbf{y} Xw=y 的最小范数解。这正是随机梯度下降(SGD)和梯度下降算法所找到的解。
我们还可以直接通过解决以下约束优化问题来尝试最大化边缘:
min
w
∥
w
∥
2
subject to
y
i
w
⊤
x
i
≥
1.
\min_{\mathbf{w}} \|\mathbf{w}\|^2 \quad \text{subject to} \quad y_i \mathbf{w}^\top \mathbf{x}_i \geq 1.
wmin∥w∥2subject toyiw⊤xi≥1.
这个优化问题构成了支持向量机的经典公式。支持向量机是一个显式正则化的例子,它明确了在训练误差为零时我们希望选择的解类型。显式正则化在高维模型中的应用历史悠久,与机器学习的发展同步。然而,在现代机器学习中,算法决策的正则化效果可能不那么明显。
尽管如此,使用隐式正则化的算法可以更快地运行。但是,重新审视经典正则化方法在现代模型中的应用,可能会带来新的洞见。
9.4.表示定理与核方法
到目前为止,我们讨论了在线性方法中,将搜索空间限制在数据张成的空间内是很常见的做法。即使当特征维度 d d d很大(甚至无限大)时,这也将搜索问题简化为一个 n n n维空间中的问题。事实证明,在广泛的通用性下,对于大多数预测中的优化问题,数据张成空间中的解是最优的。在这里,我们将正式阐述我们之前在特征讨论中首次引入的论点:对于大多数经验风险最小化(ERM)问题,最优模型将位于训练数据的张成空间中。
考虑带惩罚项的ERM问题:
minimize
1
n
∑
i
=
1
n
loss
(
w
⊤
x
i
,
y
i
)
+
λ
∥
w
∥
2
2
\text{minimize} \quad \frac{1}{n} \sum_{i=1}^{n} \text{loss}(w^\top x_i, y_i) + \lambda \|w\|_2^2
minimizen1i=1∑nloss(w⊤xi,yi)+λ∥w∥22
其中,
λ
\lambda
λ 被称为正则化参数。当
λ
=
0
\lambda = 0
λ=0 时,存在无限多个
w
w
w 可以最小化ERM问题。但对于任何
λ
>
0
\lambda > 0
λ>0,都存在一个唯一的最小化器。正则化是指在优化问题中添加一些先验信息,以使最优解唯一。在这种情况下,先验信息明确编码了我们应该尽可能选择范数较小的
w
w
w。正如我们在特征章节中讨论的那样,较小的范数在许多特征空间中往往对应于更简单的解。此外,我们还讨论了最小范数解本身在机器学习中的意义。正则化参数允许我们明确调整最优解的范数。
对于我们的带惩罚项的ERM问题,使用与上述相同的论证,我们可以将任何
w
w
w 写为:
w
=
X
⊤
β
+
v
w = X^\top \beta + v
w=X⊤β+v
其中,
β
\beta
β 和
v
v
v 是某些向量,且对于所有
i
i
i,都有
v
⊤
x
i
=
0
v^\top x_i = 0
v⊤xi=0。将这个方程代入带惩罚项的ERM问题中,我们得到:
minimize
β
,
v
1
n
∑
i
=
1
n
loss
(
β
⊤
X
x
i
,
y
i
)
+
λ
∥
X
⊤
β
∥
2
2
+
λ
∥
v
∥
2
2
\text{minimize}_{\beta,v} \quad \frac{1}{n} \sum_{i=1}^{n} \text{loss}(\beta^\top X x_i, y_i) + \lambda \|X^\top \beta\|_2^2 + \lambda \|v\|_2^2
minimizeβ,vn1i=1∑nloss(β⊤Xxi,yi)+λ∥X⊤β∥22+λ∥v∥22
现在我们可以针对
v
v
v 进行最小化,发现唯一的选择是将
v
=
0
v = 0
v=0。因此,我们必须得出最优模型位于数据的张成空间中的结论:
w
=
X
⊤
β
w = X^\top \beta
w=X⊤β
上述推导在机器学习中通常被称为表示定理(Representer Theorem)。只要成本函数(cost function)仅依赖于函数评估
f
(
x
i
)
=
w
⊤
x
i
f(x_i) = w^\top x_i
f(xi)=w⊤xi,并且成本随着
w
w
w 的二范数
∥
w
∥
2
\|w\|_2
∥w∥2 的增加而增加,那么经验风险最小化器(Empirical Risk Minimizer, ERM)将位于数据的张成空间中。
定义训练数据的核矩阵(Kernel Matrix)为
K
=
X
X
⊤
K = XX^\top
K=XX⊤。
minimize
β
1
n
∑
i
=
1
n
loss
(
e
i
⊤
K
β
,
y
i
)
+
λ
β
⊤
K
β
,
\text{minimize}_{\beta} \quad \frac{1}{n} \sum_{i=1}^{n} \text{loss}(e_i^\top K \beta, y_i) + \lambda \beta^\top K \beta,
minimizeβn1i=1∑nloss(ei⊤Kβ,yi)+λβ⊤Kβ,
其中 e i e_i ei 是标准欧几里得空间中的基向量(即,除了第 i i i 个元素为1外,其余元素均为0的向量)。因此,我们只需要使用矩阵 K K K 中的值来解决机器学习问题,只需搜索核展开中的系数 β \beta β。
表示定理(也称为核技巧)的核心思想是:即使特征空间具有更高的维度,大多数机器学习问题也可以简化为在 n n n 维空间中的搜索。此外,优化问题只关心数据点之间的点积值,而不是数据点本身的具体坐标。这促使我们在处理高维数据时采用核函数。
核函数(Kernel Function)是机器学习中处理高维数据的重要工具。它们提供了一种有效的方法来计算高维空间中向量之间的相似性,而无需显式地计算这些向量本身。通过核函数,我们可以将高维函数空间简化为训练样本中单个数据点权重的估计问题,从而大大简化了计算过程。这种能力使得核方法能够应用于各种复杂的数据集,并在许多实际应用中取得优异的性能。
10.平方损失方法与其他优化工具
本章主要聚焦于梯度方法,用于最小化经验风险,因为这些方法是当代机器学习中最常用的。然而,根据可用的计算资源和特定的应用场景,还有许多其他优化方法可能非常有用。
在机器学习中,已经证明了许多优化方法的有效性,其中最著名的是用于解决支持向量机(SVM)和相关问题的约束二次规划。在本节中,我们将重点介绍最小二乘方法,这些方法之所以吸引人,是因为它们可以通过求解线性系统来得到解。对于许多问题,线性系统求解比迭代梯度方法更快,并且计算出的解在数值精度范围内是精确的。
考虑以下优化问题:
minimize
w
1
2
∑
i
=
1
n
(
y
i
−
w
⊤
x
i
)
2
\text{minimize}_w \quad \frac{1}{2} \sum_{i=1}^{n} (y_i - \mathbf{w}^\top \mathbf{x}_i)^2
minimizew21i=1∑n(yi−w⊤xi)2
该损失函数关于
w
\mathbf{w}
w的梯度由下式给出:
−
∑
i
=
1
n
(
y
i
−
w
⊤
x
i
)
x
i
-\sum_{i=1}^{n} (y_i - \mathbf{w}^\top \mathbf{x}_i) \mathbf{x}_i
−i=1∑n(yi−w⊤xi)xi
如果我们定义
y
\mathbf{y}
y为包含所有
y
i
y_i
yi的列向量,
X
X
X为包含所有
x
i
⊤
\mathbf{x}_i^\top
xi⊤作为行的
n
×
d
n \times d
n×d矩阵,即
X
=
(
x
1
⊤
x
2
⊤
⋮
x
n
⊤
)
X = \begin{pmatrix} \mathbf{x}_1^\top \\ \mathbf{x}_2^\top \\ \vdots \\ \mathbf{x}_n^\top \end{pmatrix}
X=
x1⊤x2⊤⋮xn⊤
那么将最小二乘成本的梯度设置为零,我们得到解:
w
=
(
X
⊤
X
)
−
1
X
⊤
y
\mathbf{w} = (X^\top X)^{-1} X^\top \mathbf{y}
w=(X⊤X)−1X⊤y
对于许多问题,计算这个闭式解比运行梯度下降算法所需的大量迭代以找到具有较小经验风险的 w \mathbf{w} w更快。
正则化最小二乘也有一个方便的闭式解。使用平方损失的带惩罚项的ERM问题被称为岭回归(Ridge Regression)问题:
minimize
w
1
2
∑
i
=
1
n
(
y
i
−
w
⊤
x
i
)
2
+
λ
∥
w
∥
2
2
\text{minimize}_\mathbf{w} \quad \frac{1}{2} \sum_{i=1}^{n} (y_i - \mathbf{w}^\top \mathbf{x}_i)^2 + \lambda \|\mathbf{w}\|_2^2
minimizew21i=1∑n(yi−w⊤xi)2+λ∥w∥22
岭回归可以以与上述相同的方式求解,得到最优解:
w
=
(
X
⊤
X
+
λ
I
)
−
1
X
⊤
y
\mathbf{w} = (X^\top X + \lambda I)^{-1} X^\top \mathbf{y}
w=(X⊤X+λI)−1X⊤y
其中,
I
I
I是单位矩阵,
λ
\lambda
λ是正则化参数。
此外,还有几个其他重要的问题可以通过最小二乘方法解决。首先,我们有一个恒等式,该恒等式在处理高维数据和正则化时非常有用:
(
X
⊤
X
+
λ
I
d
)
−
1
X
⊤
=
X
⊤
(
X
X
⊤
+
λ
I
n
)
−
1
(X^\top X + \lambda I_d)^{-1} X^\top = X^\top (XX^\top + \lambda I_n)^{-1}
(X⊤X+λId)−1X⊤=X⊤(XX⊤+λIn)−1
这个恒等式允许我们在不直接计算大矩阵逆的情况下,通过较小的矩阵逆来求解问题,从而提高了计算效率。
岭回归(Ridge Regression)的求解方法提供了灵活性,允许我们通过解决不同规模的系统来找到最优解。具体来说,我们可以选择通过解决一个包含 d d d个方程和 d d d个未知数的系统来求解,或者通过解决一个包含 n n n个方程和 n n n个未知数的系统来求解。在过参数化(即 n ≫ d n \gg d n≫d)的场景下,选择具有 n n n个参数的公式更为高效。
此外,还有一个重要的问题与岭回归紧密相关,那就是最小范数插值问题(Minimum Norm Interpolation Problem),它可以表述为:
minimize
∥
w
∥
2
2
subject to
w
⊤
x
i
=
y
i
∀
i
\text{minimize} \quad \|\mathbf{w}\|_2^2 \quad \text{subject to} \quad \mathbf{w}^\top \mathbf{x}_i = y_i \quad \forall i
minimize∥w∥22subject tow⊤xi=yi∀i
这个问题旨在找到一个权重向量
w
\mathbf{w}
w,使得它对所有训练数据点的预测都精确无误(即插值),同时该向量的欧几里得范数(
ℓ
2
\ell_2
ℓ2范数)最小。这个问题有一个闭式解,即:
w
=
X
(
X
X
⊤
)
−
1
y
\mathbf{w} = X(XX^\top)^{-1}\mathbf{y}
w=X(XX⊤)−1y
这个解显示了当岭回归中的正则化参数
λ
\lambda
λ趋于零时,岭回归的解会收敛到这个最小范数解。换句话说,没有正则化的最小二乘解就是满足所有训练数据点约束的最小范数解。
最后,对于核化(kernelized)问题,我们可以将上述公式中的 X X ⊤ XX^\top XX⊤替换为适当的核矩阵 K K K。这样,最小二乘公式就可以扩展到解决任意核空间中的预测问题。这种扩展性使得最小二乘方法成为一种非常强大且灵活的工具,能够应用于从线性模型到复杂的非线性核方法的各种机器学习场景中。
11.数学优化与随机梯度方法的演进
数学优化,这一学科领域浩瀚无垠,而我们当前的探讨仅仅是这片知识海洋中的一滴水珠。为了全面而深入地掌握本章内容,包括其背后的数学严谨性及应用实施策略,我强烈推荐读者研读Wright和Recht所著的近期著作,该书提供了更为详尽和系统的阐述。
本章的核心聚焦于迭代式随机梯度方法,这些方法不仅拥有深厚的历史根基,还在当前的机器学习和模式识别领域扮演着至关重要的角色。回溯至其起源,Robbins和Monro首次提出了这些方法来求解包含随机变量的方程组,这一创新为后续的发展奠定了坚实的基础。特别是,自Rosenblatt发明感知机以来,随机梯度方法迅速成为模式识别领域的研究热点。研究人员很快意识到,感知机算法实际上是在执行一种随机逼近过程,这标志着随机梯度方法在解决实际问题方面迈出了重要一步。
然而,随着研究的深入,研究人员也发现了感知机算法的局限性。特别是当处理不可分数据时,传统的感知机步长策略无法确保收敛到全局最优解。为了克服这一难题,研究者们开始探索新的方法,其中Widrow-Hoff提出的“最小均方”(LMS)规则尤为引人注目。这一规则通过随机梯度下降来最小化与平方损失相关的经验风险,为优化问题提供了一种有效的解决方案。
进一步地,Aizerman及其同事不仅将随机梯度下降方法应用于线性函数,还成功地将其拓展至核空间,进一步拓宽了这些方法的适用范围。这些研究不仅展示了随机梯度方法的灵活性和强大功能,也推动了优化理论的不断发展。
值得注意的是,尽管这些方法在表面上看起来各不相同,但它们之间却存在着深刻的内在联系。然而,要真正将这些方法统一起来并形成一个完整的理论体系,却需要经历漫长而艰难的探索过程。直到20世纪80年代,随着复杂性理论的逐步成熟和完善,Nemirovski和Yudin才成功地为随机梯度方法找到了最优步长策略。这一突破不仅为随机梯度方法的应用提供了更加坚实的理论基础,也为其在更广泛领域内的推广和应用创造了条件。
更为令人瞩目的是,直到21世纪初的2007年,感知机算法的第一个非渐近分析才得以问世。这一成果不仅揭示了感知机算法在收敛性和稳定性方面的更多细节和特性,也为我们深入理解随机梯度方法的本质和机理提供了新的视角和思路。
在机器学习的发展历程中,优化方法的选择与变迁构成了一幅引人入胜的画卷。尤其值得注意的是,直到21世纪的曙光初现,随机梯度下降(SGD)才逐渐确立了其在机器学习领域的核心地位,成为众多算法的首选优化方法。这一转变并非一蹴而就,而是伴随着各种优化方法之间的激烈竞争与周期性复兴。
回望历史,我们可以清晰地看到优化方法流行的周期性模式。在20世纪60年代,线性规划等全局优化方法以其在模式识别领域的卓越表现赢得了广泛的认可与推崇。这些方法凭借其强大的理论支撑和高效的计算能力,一度将随机下降方法挤出了主流舞台。然而,随着技术的不断进步和应用场景的不断拓展,优化方法的竞争格局也在悄然发生变化。
时间跳转到20世纪80年代,随机梯度下降以一种全新的面貌——反向传播(Backpropagation)——重新回到了人们的视野中。这一时期的反向传播算法凭借其灵活性和适用性,在神经网络训练中大放异彩,极大地推动了机器学习领域的发展。然而,好景不长,随着全局优化方法的不断改进和完善,它们再次占据了优化方法的主导地位。
值得注意的是,在这一系列的历史变迁中,Mangasarian等先驱者始终保持着敏锐的洞察力和深刻的思考。他们通过私人通信等方式分享了自己的见解和观察,认为就计算速度和解决方案质量而言,线性规划等方法在某些情况下仍然具有不可替代的优势。这些观点不仅为我们提供了宝贵的历史参考,也促使我们更加全面地审视当前机器学习领域的优化方法选择。
更为引人深思的是,Nemirovski和Nesterov等优化领域的巨擘在迭代梯度和随机梯度方法方面做出了开创性的贡献。然而,他们并未止步于此,而是迅速将目光投向了更广阔的全局优化领域,致力于发展内点法等更为高效和强大的优化方法。这一转变不仅展现了他们深邃的学术洞察力和前瞻性的研究视野,也为机器学习领域的深度优化奠定了坚实的基础。
如今,当我们站在21世纪的门槛上回望过去时,不难发现那些曾经被遗忘或取代的优化方法仍然蕴含着巨大的潜力和价值。随着机器学习应用场景的不断拓展和复杂化,我们或许需要重新审视这些非迭代方法,探索它们在新的时代背景下所能发挥的独特作用。通过深度优化和跨学科融合等手段,我们有理由相信这些传统方法将在未来的机器学习领域中焕发出新的生机与活力。