1.前言
从更深入的理论层面来看,梯度的计算在数学原理上必然需要借助求导数这一关键操作来实现精确的计算。然而,在图像处理领域中,图像梯度的计算方式具有其独特性。具体而言,是通过对相邻像素值的差进行计算,从而得到梯度的近似值。这种近似计算方法虽然在一定程度上简化了计算过程,但却能够较为有效地反映图像的基本特征。
图像梯度所代表的含义不仅仅是简单的图像变化速率,它更像是图像内在信息的一种外在表现形式,深刻地反映了图像的边缘信息。边缘作为图像中一个极为重要的特征区域,是像素值发生快速变化的关键位置。所以,当我们聚焦于图像的边缘部分时,会发现其灰度值呈现出较为明显的变化幅度,这种大幅度的变化直接导致了梯度值相对较大。与之形成鲜明对比的是,图像中那些相对较平滑的部分,其像素值的变化较为平缓,灰度值的变化程度较小,进而使得梯度值也处于较小的水平。
在实际的图像处理应用中,为了能够准确地检测出图像的边缘,我们的核心任务是检测图像中的不连续性。而图像梯度恰好为我们提供了一种有效的检测手段,它能够敏锐地捕捉到这种不连续性的存在。然而,我们也必须清醒地认识到,图像梯度在实际应用过程中并非毫无瑕疵。由于图像在采集、传输等过程中可能会受到各种因素的干扰,其中噪声的影响尤为突出。噪声的存在会对图像梯度的计算结果产生干扰,从而影响边缘检测的准确性。因此,为了提高边缘检测的精度和可靠性,在进行边缘检测之前,建议先对图像进行平滑处理。这种平滑处理可以有效地去除或减轻噪声的影响,使得图像梯度能够更准确地反映图像的真实边缘信息,为后续的图像处理和分析工作奠定坚实的基础。
2.梯度算子
2.1 Sobel算子
2.1.1 原理与计算
Sobel算子是一种在图像处理和计算机视觉中常用的边缘检测算子,由Irving Sobel在1968年提出。它通过计算图像亮度的空间梯度来突出边缘,特别适用于检测图像中的水平和垂直边缘。Sobel算子基于局部梯度的概念,使用两个3x3的卷积核(一个用于水平方向,一个用于垂直方向)来近似图像的一阶导数。
2.1.2 卷积核的构成:
Sobel算子包含两个3×3的卷积核,一个用于检测水平方向的边缘,另一个用于检测垂直方向的边缘。水平方向和垂直方向的卷积核通常为:
-
水平方向卷积核(Gx):
G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] Gx = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} Gx= −1−2−1000121 -
垂直方向卷积核(Gy):
G y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] Gy = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} Gy= −101−202−101
注意:
Gx 用于检测纵向边缘,Gy 用于检测横向边缘。
对x方向求导,得到的是y方向的边缘。垂直方向的边缘在水平方向的梯度(偏导数)幅值较大。
对y方向求导,得到的是x方向的边缘。水平方向的边缘在垂直方向的梯度(偏导数)幅值较大。
2.1.3 计算梯度近似值的过程:
当对图像进行处理时,将这些卷积核在图像上滑动。以水平方向卷积核为例,在图像的每个3×3区域内,将卷积核的每个元素与对应位置的像素值相乘,然后将这些乘积相加,得到该区域在水平方向的梯度近似值。同理,使用垂直方向卷积核可得到垂直方向的梯度近似值。最后,可以根据水平和垂直方向的梯度近似值来计算总的梯度幅值和方向,从而确定边缘的位置和强度。例如,对于图像中某个3×3像素块,假设其像素值分别为:
[ 10 20 30 40 50 60 70 80 90 ] \begin{bmatrix} 10 & 20 & 30 \\ 40 & 50 & 60 \\ 70 & 80 & 90 \end{bmatrix} 104070205080306090
使用水平方向Sobel卷积核计算得到的梯度近似值为: ( − 1 × 10 + 0 × 20 + 1 × 30 ) + ( − 2 × 40 + 0 × 50 + 2 × 60 ) + ( − 1 × 70 + 0 × 80 + 1 × 90 ) = 20 (-1×10 + 0×20 + 1×30)+(-2×40 + 0×50 + 2×60)+(-1×70 + 0×80 + 1×90)=20 (−1×10+0×20+1×30)+(−2×40+0×50+2×60)+(−1×70+0×80+1×90)=20。类似地,可以计算垂直方向的梯度近似值。这种计算方式在图像的每一个局部区域重复进行,从而实现对整个图像边缘的检测。
G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] X [ p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8 p 9 ] Gx = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} X \begin{bmatrix} p1 & p2 & p3 \\ p4 & p5 & p6 \\ p7 & p8 & p9 \end{bmatrix} Gx= −1−2−1000121 X p1p4p7p2p5p8p3p6p9
计算像素点P5的梯度,需要利用邻域内的像素点,公式为:
P 5 x = ( P 3 − P 1 ) + 2 ( P 6 − P 4 ) + ( P 9 − P 7 ) P5x=(P3−P1)+2(P6−P4)+(P9−P7) P5x=(P3−P1)+2(P6−P4)+(P9−P7)
即用像素点P5右侧像素值减去左侧像素值,距离P5近的点权重较大,为2;距离P5远的点权重较小,为1。
2.1.4 计算垂直方向偏导数的近似值
设原图像大小为,垂直方向偏导数为:
G x = [ − 1 − 2 − 1 0 0 0 1 2 1 ] X [ p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8 p 9 ] Gx =\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} X \begin{bmatrix} p1 & p2 & p3 \\ p4 & p5 & p6 \\ p7 & p8 & p9 \end{bmatrix} Gx= −101−202−101 X p1p4p7p2p5p8p3p6p9
计算像素点P5的梯度,需要利用邻域内的像素点,公式为:
P 5 y = ( P 7 − P 1 ) + 2 ( P 8 − P 2 ) + ( P 9 − P 3 ) P5y=(P7−P1)+2(P8−P2)+(P9−P3) P5y=(P7−P1)+2(P8−P2)+(P9−P3)
即用像素点P5下一行的像素值减去上一行的像素值,距离P5近的点权重较大,为2;距离P5远的点权重较小,为1。
2.1.5 Python代码实现
OpenCV使用Sobel 算子的方法是cv2.Sobel()
dst = cv2.Sobel(src, ddepth, dx, dy, ksize=3, scale=1, delta=0, borderType=cv2.BORDER_DEFAULT)
参数:
- src:输入图像,通常为灰度图像。
- ddepth:输出图像的深度。选择 cv2.CV_64F 可以保持更高的精度。具体关系:
| 输入图像深度(src.depth()) | 输出图像深度(ddepth) |
|---|---|
| CV_8U | -1/CV_16S/CV_32F/CV_64F |
| CV_16U/CV_16S | -1/CV_32F/CV_64F |
| CV_32F | -1/CV_32F/CV_64F |
| CV_64F | -1/CV_64F |
- dx:x 方向的导数阶数(0 或 1),dx=1 、dy=0表示计算 x 方向的导数。
- dy:y 方向的导数阶数(0 或 1),dy=1 、dx=0表示计算 y 方向的导数。
- ksize:Sobel卷积核核的大小,通常为 1、3、5 或 7。该值为-1时,会使用Scharr算子进行运算
- scale:用于缩放输出梯度的值,默认为1,是没有缩放的
- delta:加到输出结果上的值,默认为0
- borderType:边界样式,默认值为cv2.BORDER_DEFAULT
参数ddepth:
该值为-1时,让处理结果与原始图像保持一致,但是直接将ddepth设置为-1,得到的结果可能是错误的。计算梯度值可能出现负数,当处理的图像是8位图类型,ddepth的值为-1时,运算结果也是8位图类型,负数会自动截断为0,发生信息丢失。为了避免信息丢失,要先使用更高的数据类型cv2.CV_64F,再通过取绝对值将其映射到cv2.CV_8U类型。所以,通常将ddepth值设置为“cv2.CV_8U”,并使用函数cv2.convertScaleAbs()对函数cv2.Sobel()的计算结果取绝对值。
注意: x方向和y方向的边缘叠加时,应先令dx=1,dy=0,得到一个结果;再令dx=0,dy=1,得到一个结果。将两个结果分别取绝对值(转换成uint8),然后线性混合。而不是同时令dx=1和dy=1。
dx=1,dy=0,表示计算X方向的导数,检测出的是垂直方向上的边缘;dx=0,dy=1,表示计算Y方向的导数,检测出的是水平方向上的边缘。
代码示例:
# -*- coding: utf-8 -*-
import cv2
# 读取图像
img = cv2.imread('../1.jpg', 0)
# 计算 x 方向的导数,得到 y 方向的边缘
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0)
# 计算 y 方向的导数,得到 x 方向的边缘
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1)
# 求绝对值
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.convertScaleAbs(sobely)
# x方向和y方向的边缘叠加
sobelxy = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0) # 加权合成,第二和第四个参数是权重系数,最后一个是加到结果上的标量值(常用于调整亮度)
# 显示图像
cv2.imshow("origin image", img)
cv2.imshow("x", sobelx)
cv2.imshow("y", sobely)
cv2.imshow("xy", sobelxy)
cv2.waitKey(0)
cv2.destroyAllWindows()
2.1.6 C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("xy.jpg", cv::IMREAD_GRAYSCALE);
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
cv::Mat gradX, gradY, absGradX, absGradY, sobel;
// 计算 x 方向的导数
cv::Sobel(image, gradX, CV_64F, 1, 0);
// 计算 y 方向的导数
cv::Sobel(image, gradY, CV_64F, 0, 1);
// 将结果转换为绝对值
cv::convertScaleAbs(gradX, absGradX);
cv::convertScaleAbs(gradY, absGradY);
// 合并 x 和 y 方向的结果
cv::addWeighted(absGradX, 0.5, absGradY, 0.5, 0, sobel);
cv::imshow("src", image);
cv::imshow("X", absGradX);
cv::imshow("Y", absGradY);
cv::imshow("XY", sobel);
cv::waitKey(0);
cv::destroyAllWindows();
}
2.1.7 效果图
原图:
X方向:
Y方向:
XY方向:
2.2 Scharr算子
Scharr算子是一种用于图像边缘检测的算子,类似于Sobel算子,但在某些情况下能提供更好的结果。Scharr算子通过更高的权重计算邻域像素的梯度,从而提高对边缘的敏感度。
2.2.1 Scharr算子的定义
Scharr算子是一种在图像处理中用于边缘检测的算子,它与Sobel算子类似,但具有更好的性能,尤其是在处理边缘方向不明显的图像时。
Scharr算子通过计算图像在水平方向(x方向)和垂直方向(y方向)的梯度来检测边缘。边缘通常对应于图像梯度的最大值。Scharr算子使用卷积核来计算图像的导数,从而得到梯度的幅值(边缘强度)和方向。Scharr算子在噪声敏感性和梯度精度方面表现更好,特别适合处理含有高噪声的图像。
2.2.2 卷积核
Scharr算子使用的卷积核如下:
- 水平方向的卷积核(Gx):
G x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] Gx = \begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3 \end{bmatrix} Gx= −3−10−30003103 - 垂直方向的卷积核(Gy):
G y = [ − 3 − 10 − 3 0 0 0 3 10 3 ] Gy = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3 \end{bmatrix} Gy= −303−10010−303
2.2.3 卷积操作
将卷积核与图像进行卷积运算,分别计算出图像在x方向和y方向的梯度。对于每个像素点,用相应的卷积核在局部区域内进行加权求和,得到该点在x方向和y方向的梯度值。
2.2.4 梯度幅值与方向
通过计算出的梯度值,可以得到梯度的幅值(边缘强度)和方向。梯度幅值(G)和梯度方向(θ)可以通过以下公式计算:
G
=
G
x
2
+
G
y
2
G = \sqrt{Gx^2 + Gy^2}
G=Gx2+Gy2
θ
=
arctan
(
G
y
G
x
)
\theta = \arctan\left(\frac{Gy}{Gx}\right)
θ=arctan(GxGy)
2.2.5 Python代码实现
OpenCV使用Scharr算子的函数是cv2.Scharr()
dst = cv2.Scharr(src, ddepth, dx, dy, scale=1, delta=0, borderType=cv2.BORDER_DEFAULT)```
参数:
- src:输入图像,通常为灰度图像。
- ddepth:输出图像的数据深度,该值与函数cv2.Sobel()中的参数ddepth的含义相同。常用 cv2.CV_64F可以避免溢出。
- dx:x 方向的导数阶数(0 或 1),dx=1 表示计算 x 方向的导数。
- dy:y 方向的导数阶数(0 或 1),dy=1 表示计算 y 方向的导数。
- scale:缩放结果的因子,默认为 1。
- delta:加到输出结果上的值,默认为 0。
- borderType:边界处理方式,默认为 cv2.BORDER_DEFAULT。
在cv2.Sobel()中,ksize=-1时,则会使用Scharr算子。所以下面两个语句等价:
dst = cv2.Scharr(src,ddepth,dx,dy)
dst = cv2.Sobel(src,ddepth,dx,dy,-1)
注意:
- 参数ddepth的值应该设置为“cv2.CV_64F”,并对函数cv2.Scharr()的计算结果取绝对值。
- dx和dy不能同时为1,否则语句是错误的。
- 计算x方向和y方向的边缘叠加时,应先令dx=1,dy=0,得到一个结果;再令dx=0,dy=1,得到一个结果。将两个结果相加,而不是同时令dx=1和dy=1。
import cv2
#读取图像
img = cv2.imread('xy.jpg',0)
# 计算 x 方向的导数,得到 y 方向的边缘
scharrx = cv2.Scharr(img, cv2.CV_64F, 1, 0)
# 计算 y 方向的导数,得到 x 方向的边缘
scharry = cv2.Scharr(img, cv2.CV_64F, 0, 1)
# 求绝对值
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
# x方向和y方向的边缘叠加
scharrxy = cv2.addWeighted(scharrx, 0.5, scharry, 0.5, 0) # 加权合成,第二和第四个参数是权重系数,最后一个是加到结果上的标量值(常用于调整亮度)
# 显示图像
cv2.imshow("origin image", img)
cv2.imshow("x", scharrx)
cv2.imshow("y", scharry)
cv2.imshow("xy", scharrxy)
cv2.waitKey(0)
cv2.destroyAllWindows()
2.1.6 C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("xy.jpg", cv::IMREAD_GRAYSCALE);
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
cv::Mat gradX, gradY, absGradX, absGradY, sobel;
// 计算 x 方向的导数
cv::Scharr(image, gradX, CV_64F, 1, 0);
// 计算 y 方向的导数
cv::Scharr(image, gradY, CV_64F, 0, 1);
// 将结果转换为绝对值
cv::convertScaleAbs(gradX, absGradX);
cv::convertScaleAbs(gradY, absGradY);
// 合并 x 和 y 方向的结果
cv::addWeighted(absGradX, 0.5, absGradY, 0.5, 0, scharr);
cv::imshow("src", image);
cv::imshow("X", absGradX);
cv::imshow("Y", absGradY);
cv::imshow("XY", scharr);
cv::waitKey(0);
cv::destroyAllWindows();
}
2.1.7 效果图
原图:
X方向:
Y方向:
XY方向:
2.3 Roberts算子
Roberts算子是一种用于图像边缘检测的算子,由Lawrence Roberts在1963年提出。它基于局部差分的原理,通过计算图像上相邻像素点之间的差异来检测边缘。Roberts算子特别适合于检测接近正45度或负45度的边缘,并且对陡峭的低噪声图像效果较好。Roberts算子的计算过程简单快速,只需要考虑四个相邻像素,且仅使用加减运算,无需复杂的乘法和除法。它能够较好地增强正负45度的图像边缘。但缺点是Roberts算子对噪声非常敏感,且由于其使用的核很小,它产生的边缘响应较弱,除非边缘非常锐利。此外,它不能提供边缘的精确位置和宽度,因此常常作为边缘检测的预处理步骤。
Roberts算子常用于图像处理和计算机视觉中的初步边缘检测,尤其是在需要快速计算梯度幅值和方向时。它也可以作为其他边缘检测技术的预处理步骤,用于提取初步的边缘信息。
基本原理
Roberts算子使用两个2x2的模板进行卷积操作,分别为:
- 水平方向模板(Gx):
G x = [ 1 0 0 − 1 ] Gx = \begin{bmatrix}1 & 0 \\0 & -1\end{bmatrix} Gx=[100−1] - 垂直方向模板(Gy):
G y = [ 0 1 − 1 0 ] Gy = \begin{bmatrix}0 & 1 \\-1 & 0\end{bmatrix} Gy=[0−110]
这两个模板分别对应水平和垂直边缘的检测。通过将这两个模板与图像进行卷积运算,可以得到水平和垂直边缘方向上的边缘响应值。
计算过程
对于图像中的每个像素点,Roberts算子计算该点在水平和垂直方向上的梯度值。梯度值可以通过以下方式计算:
- 水平方向梯度(gx):
g x = P 1 − P 3 gx = P1 - P3 gx=P1−P3 - 垂直方向梯度(gy):
g y = P 2 − P 4 gy = P2 - P4 gy=P2−P4
其中, P 1 , P 2 , P 3 , P 4 P1, P2, P3, P4 P1,P2,P3,P4是像素点周围的四个相邻像素值。
然后,可以计算梯度的幅值(边缘强度):
G
=
g
x
2
+
g
y
2
G = \sqrt{gx^2 + gy^2}
G=gx2+gy2
Python实现
在 Python 中,Roberts 算子主要通过 Numpy 定义卷积模板,再调用 OpenCV 的 filter2D() 函数实现边缘提取。
cv2.filter2D 是 OpenCV 中用于对图像应用自定义卷积核的函数。该函数通过卷积操作将一个指定的卷积核应用于输入图像,从而生成一个新的图像。
cv2.filter2D(src, ddepth, kernel, dst=None, anchor=(-1, -1), delta=0, borderType=cv2.BORDER_DEFAULT)
参数
- src:输入图像,通常为单通道或多通道的图像。
- ddepth:输出图像的数据深度,可以是 cv2.CV_8U, cv2.CV_16S, cv2.CV_64F 等,表示输出图像的像素数据类型。
- kernel:卷积核,通常是一个 NumPy 数组,定义了如何处理输入图像的每个像素。
- dst:输出图像,可以设置为 None,表示在函数内部分配内存。
- anchor:卷积核的锚点,默认为 (-1, -1),表示锚点位于卷积核的中心。
- delta:加到输出结果上的值,默认为 0。
- borderType:边界处理方式,决定如何处理图像边界,默认为 cv2.BORDER_DEFAULT。
# -*- coding: utf-8 -*-
import cv2
import numpy as np
img = cv2.imread('../1.jpg', cv2.IMREAD_GRAYSCALE)
# Roberts 算子卷积核
kernel_x = np.array([[1, 0], [0, -1]], dtype=np.float32)
kernel_y = np.array([[0, 1], [-1, 0]], dtype=np.float32)
# 应用卷积
roberts_x = cv2.filter2D(img, cv2.CV_64F, kernel_x)
roberts_y = cv2.filter2D(img, cv2.CV_64F, kernel_x)
# 数据格式转换
absX = cv2.convertScaleAbs(roberts_x)
absY = cv2.convertScaleAbs(roberts_y)
# 叠加
roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
cv2.imshow('roberts', roberts)
cv2.waitKey(0)
cv2.destroyAllWindows()
C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("../1.jpg", cv::IMREAD_GRAYSCALE);
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
// 定义 Roberts 算子的卷积核
cv::Mat kernel_x = (cv::Mat_<float>(2, 2) << 1, 0, 0, -1);//创建并初始化矩阵
cv::Mat kernel_y = (cv::Mat_<float>(2, 2) << 0, 1, -1, 0);
//应用卷积
cv::Mat roberts_x, roberts_y, roberts;
cv::filter2D(image, roberts_x, CV_64F, kernel_x);
cv::filter2D(image, roberts_y, CV_64F, kernel_y);
cv::convertScaleAbs(roberts_x, roberts_x);
cv::convertScaleAbs(roberts_y, roberts_y);
cv::addWeighted(roberts_x, 0.5, roberts_y, 0.5, 0, roberts);
cv::imshow("robers", roberts);
cv::waitKey(0);
cv::destroyAllWindows();
}
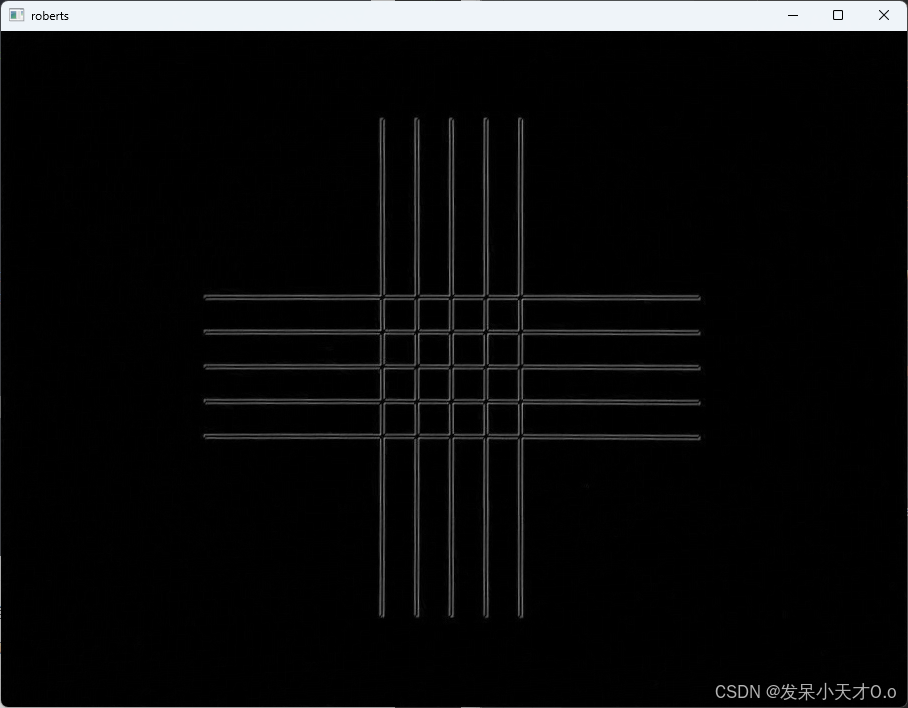
实现效果
2.4 Laplacian算子
Laplacian算子是一种在图像处理中常用的二阶微分算子,主要用于边缘检测和图像增强。Laplacian算子基于图像的二阶导数,强调图像中灰度的突变,用于检测图像中的边缘和纹理特征。数学上,Laplacian算子定义为:
∇
2
f
=
∂
2
f
∂
x
2
+
∂
2
f
∂
y
2
\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}
∇2f=∂x2∂2f+∂y2∂2f
其中,
f
(
x
,
y
)
f(x, y)
f(x,y) 是图像的灰度值函数,而
∂
2
f
∂
x
2
\frac{\partial^2 f}{\partial x^2}
∂x2∂2f 和
∂
2
f
∂
y
2
\frac{\partial^2 f}{\partial y^2}
∂y2∂2f 分别表示图像在x和y方向上的二阶偏导数。通过计算这两个偏导数的和,可以找到图像中的边缘和纹理特征。
Laplacian算子是一种特别容易受到噪声干扰的边缘发现算子,所以经常对要处理的图像首先进行一个高斯模糊,然后再进行拉普拉斯算子的边缘提取。先进行高斯滤波,再使用拉普拉斯算子的过程统称为LoG(Laplace of Gaussian function)算子。
与一阶导数(如 Sobel 和 Roberts 算子)相比,Laplacian 算子对图像中的边缘更敏感,因为它能够捕捉到更细微的变化。
计算过程
在数字图像处理中,Laplacian算子可以通过卷积运算来近似表示。常用的Laplacian算子的离散形式如下:
[
0
1
0
1
−
4
1
0
1
0
]
\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}
0101−41010
这个卷积核对图像进行卷积操作,从而得到边缘信息。计算过程中,将卷积核应用于图像的每一个像素点,计算中心点的上下左右的值之和,减去中心值,得到该点的Laplacian值。
Python代码实现
OpenCV使用Laplacian算子的函数是cv2.Laplacian()
dst = cv2.Laplacian(src, ddepth, ksize=3, scale=1, delta=0, borderType=cv2.BORDER_DEFAULT)
参数:
- src:输入图像,通常为灰度图像。
- ddepth:输出图像的数据深度,该值与函数cv2.Sobel()中的参数ddepth的含义相同。常用 cv2.CV_64F可以避免溢出。
- ksize:用于计算 Laplacian 的 Sobel 卷积核大小,默认为 3。可以选择 1、3、5、7 等。
- scale:缩放结果的因子,默认为 1。
- delta:加到输出结果上的值,默认为 0。
- borderType:边界处理方式,默认为 cv2.BORDER_DEFAULT。
import cv2
# 读取图像并转换为灰度
img = cv2.imread('../1.jpg', cv2.IMREAD_GRAYSCALE)
# 使用 Laplacian 算子进行边缘检测
laplacian = cv2.Laplacian(img, cv2.CV_64F)
# 转换为绝对值并将其转换为 8 位图像
laplacian_abs = cv2.convertScaleAbs(laplacian)
# 显示结果
cv2.imshow('Original Image', img)
cv2.imshow('Laplacian Edge Detection', laplacian_abs)
cv2.waitKey(0)
cv2.destroyAllWindows()
C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("../1.jpg", cv::IMREAD_GRAYSCALE);
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
cv::Mat laplacian, laplacian_abs;
cv::Laplacian(image, laplacian, CV_64F);
cv::convertScaleAbs(laplacian, laplacian_abs);
cv::imshow("src", image);
cv::imshow("Laplacian Edge Detection", laplacian_abs);
cv::waitKey(0);
cv::destroyAllWindows();
}
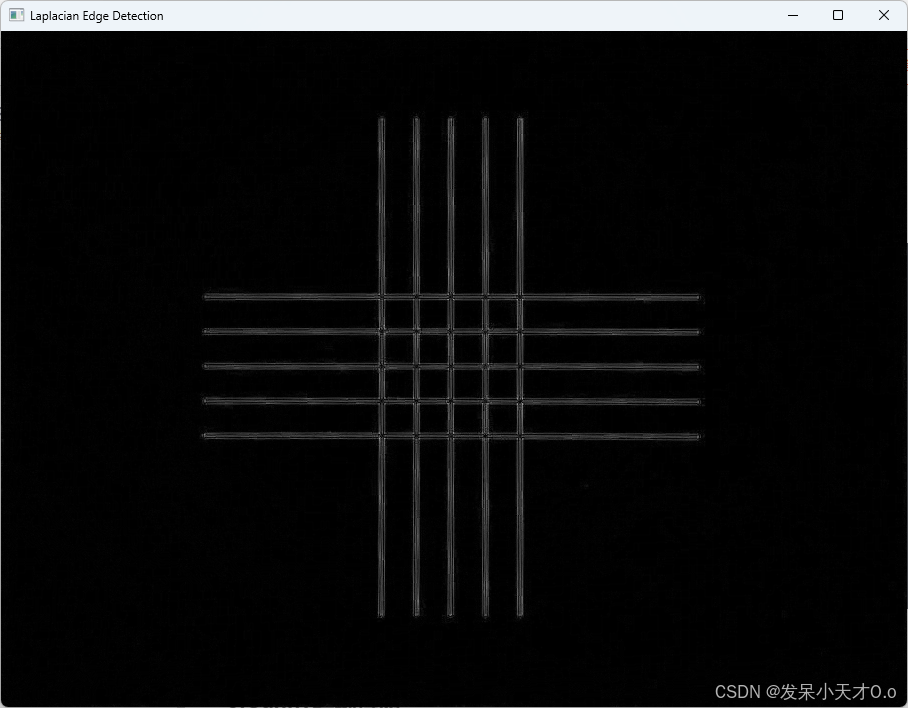
效果图
3.Canny边缘检测
Canny边缘检测是一种多级边缘检测算法。于1986年由John F. Canny在论文《A Computational Approach to Edge Detection》中提出。
Canny边缘检测是从不同视觉对象中提取有用的结构信息并大大减少要处理的数据量的一种技术,目前已广泛应用于各种计算机视觉系统。Canny发现,在不同视觉系统上对边缘检测的要求较为类似,因此,可以实现一种具有广泛应用意义的边缘检测技术。边缘检测的一般标准包括:
- 以低的错误率检测边缘,也即意味着需要尽可能准确的捕获图像中尽可能多的边缘。
- 检测到的边缘应精确定位在真实边缘的中心。
- 图像中给定的边缘应只被标记一次,并且在可能的情况下,图像的噪声不应产生假的边缘。
为了满足这些要求,Canny使用了变分法。Canny检测器中的最优函数使用四个指数项的和来描述,它可以由高斯函数的一阶导数来近似。
在目前常用的边缘检测方法中,Canny边缘检测算法是具有严格定义的,可以提供良好可靠检测的方法之一。由于它具有满足边缘检测的三个标准和实现过程简单的优势,成为边缘检测最流行的算法之一。
完成一个Canny边缘检测算法可以分为以下四步:
- 1.利用高斯滤波去噪。噪声会影响边缘检测的准确性,因此要先将噪声过滤掉。
- 2.计算梯度幅值和方向。
- 3.非极大值抑制,即适当地让边缘“变瘦”。
- 4.应用双阈值确定真实的和可能的边缘。
3.1 高斯滤波
它使用高斯函数作为权重系数对邻域内的像素进行加权平均,以实现图像的平滑和去噪。高斯滤波基于高斯分布,这是一种在自然和科技领域中常见的概率分布,因其钟形曲线而被称为“钟形曲线”。
高斯滤波可以有效地去除图像中的高斯噪声。用于减少图像中的高频细节,使图像看起来更平滑。与其他滤波器相比,高斯滤波在平滑图像的同时,能够较好地保留边缘信息。
高斯滤波是一种线性滤波器,计算简单,效果稳定,对图像的亮度影响小。高斯滤波可能会模糊图像的边缘,因为它对所有频率的信号都进行了衰减。
高斯函数
高斯函数的数学表达式为:
G
(
x
)
=
1
σ
2
π
e
−
x
2
2
σ
2
G(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{x^2}{2\sigma^2}}
G(x)=σ2π1e−2σ2x2
其中,
σ
\sigma
σ 是标准差,控制着高斯分布的宽度。
σ
\sigma
σ 越大,曲线越宽,权重分布越平坦;
σ
\sigma
σ 越小,曲线越窄,权重分布越集中。
高斯滤波器
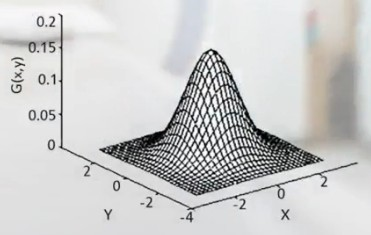
在二维图像处理中,高斯滤波器是一个二维高斯函数,其表达式为:
G
(
x
,
y
)
=
1
2
π
σ
2
e
−
x
2
+
y
2
2
σ
2
G(x, y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2 + y^2}{2\sigma^2}}
G(x,y)=2πσ21e−2σ2x2+y2
这个函数描述了在图像中每个像素点 ( (x, y) ) 处的权重。
实现步骤
- 选择高斯核大小和标准差:核大小决定了滤波器覆盖的邻域范围,标准差决定了权重分布的形状。
- 创建高斯核:根据选择的标准差,计算核中每个元素的权重。
- 归一化:确保核中所有权重的和为1,以保持图像的亮度不变。
- 卷积操作:将高斯核与图像进行卷积,即对每个像素点,将其邻域内的像素值乘以对应的高斯权重,然后求和,得到新的像素值。
3.2 计算梯度强度和方向
在图像处理中,梯度的方向通常与边缘的方向垂直。这是因为梯度向量指向图像亮度变化最快的方向,而边缘则是亮度变化最显著的地方。
使用边缘检测算子(如Roberts、Sobel、Scharr等)计算图像中的水平、垂直和对角方向的梯度,可以帮助确定像素点的梯度大小和方向。梯度的大小 G G G 和方向 θ \theta θ 可以通过以下公式计算:
G
=
G
x
2
+
G
y
2
(1)
G = \sqrt{G_x^2 + G_y^2} \quad \text{(1)}
G=Gx2+Gy2(1)
θ
=
arctan
(
G
y
G
x
)
(2)
\theta = \arctan\left(\frac{G_y}{G_x}\right) \quad \text{(2)}
θ=arctan(GxGy)(2)
其中, G x 和 G y G_x 和 G_y Gx和Gy分别是图像在水平和垂直方向上的一阶导数, G G G 是梯度的大小, θ \theta θ 是梯度的方向, arctan \arctan arctan 是反正切函数。
通过这些计算,可以得到一个包含梯度大小和方向信息的矩阵。这个矩阵可以用于进一步的图像处理任务,如边缘连接、边缘跟踪和特征提取等。
在实际应用中,这些梯度信息通常用于生成边缘图,其中梯度大小较大的像素点被标记为边缘。此外,梯度方向信息也可以用来平滑边缘或进行其他形式的图像分析。
梯度的大小和方向是图像边缘检测中的关键信息,通过计算这些信息,我们可以有效地识别和分析图像中的边缘。
梯度的方向通常就近取值为水平(左、右)、垂直(上、下)、对角线(右上、左上、左下、右下)等 8 个不同的方向。
角度的确定
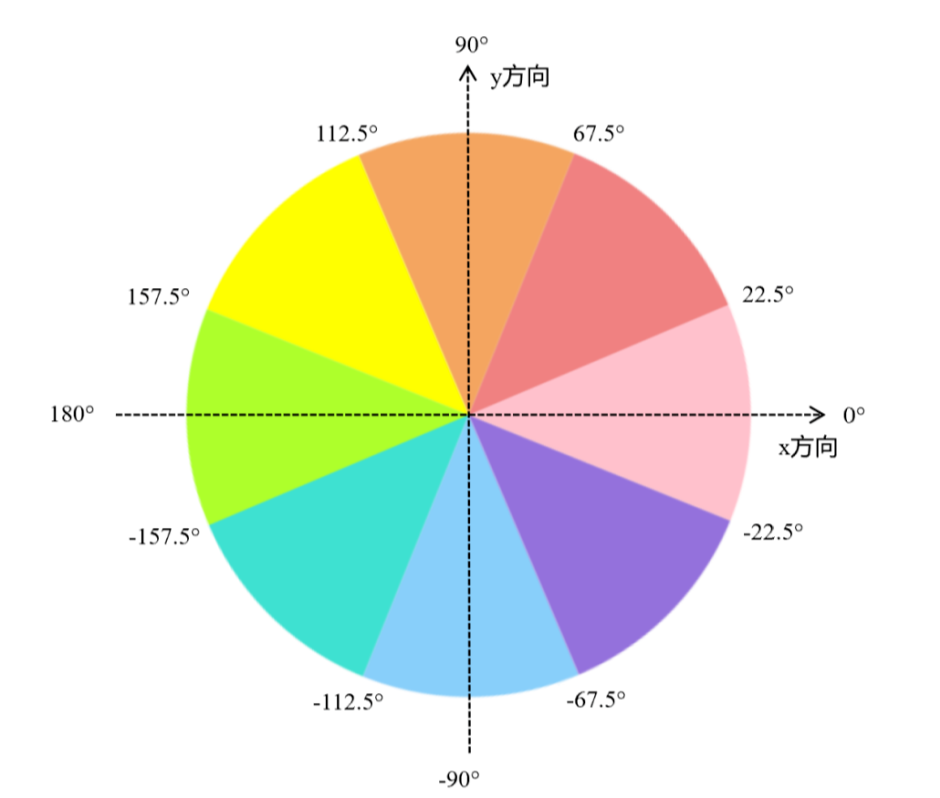
通过(2)式求出的角度一般不在前边指定的8个方向上,需要将角度分类到这四条线(0、45、90、135 度)分成的八个区域中。
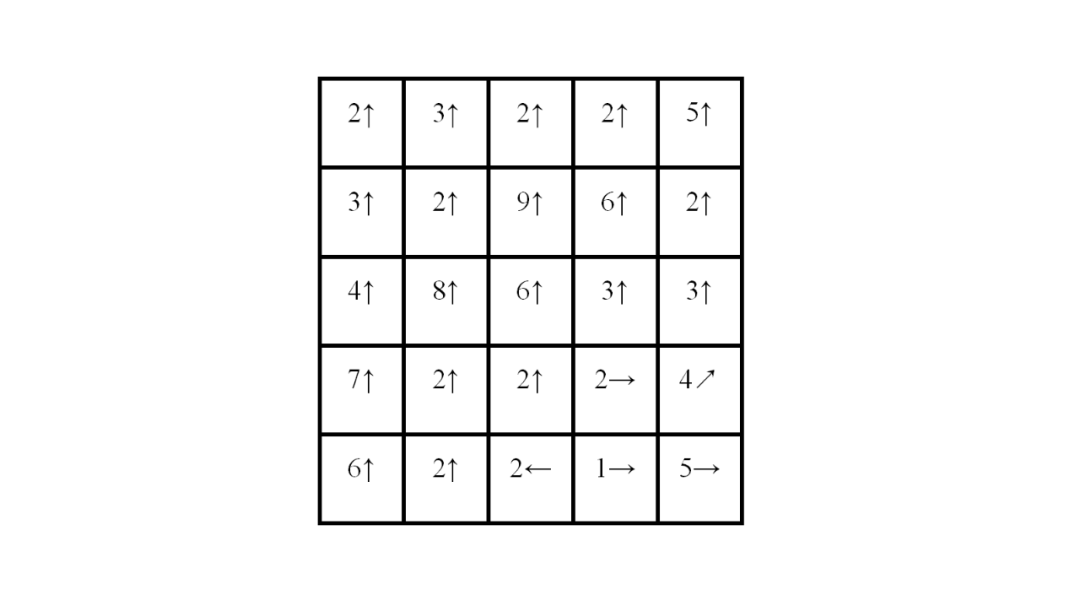
根据给定的角度线(0、45、90、135 度),可以定义八个方向的区间:
- 0-22.5 度 -> 0度
- 22.5-67.5 度 -> 45度
- 67.5-112.5 度 -> 90度
- 112.5-157.5 度 -> 135度
- 157.5-180度 -> 0度(与0度重合)
- -180到-157.5 -> 135度
- -157.5到-112.5 -> 90度
- -112.5到-67.5 -> 45度
- -67.5到-22.5 -> 0度
- -22.5到0 -> 0度
八个区域如下图:
3.3 非极大值抑制(NMS)
非极大值抑制(Non-Maximum Suppression, NMS)是边缘检测中的一个关键步骤,用于细化边缘并确保边缘是单像素宽。非极大值抑制的目的是保留局部梯度最大的点,这些点最有可能是真实的边缘。该过程基于梯度的方向,对于每个像素点,比较其梯度值与其在梯度方向上的相邻像素点的梯度值。
首先,使用边缘检测算子(如Sobel、Scharr等)计算图像中每个像素点的梯度幅值和方向。对于每个像素点,根据其梯度方向,确定其在梯度方向上的两个相邻像素点。 如果中心像素点的梯度值大于其在梯度方向上的两个相邻像素点的梯度值,则认为该点是局部最大值,保留该点。如果不是,将该点的梯度值置为0,表示抑制该点。
经过非极大值抑制处理后,图像中的边缘被细化,每个边缘点都是局部梯度最大的点,从而得到更清晰、更准确的边缘。
非极大值抑制的效果是使边缘变得更细,并且抑制了非边缘的噪声点。这不仅提高了边缘检测的准确性,还减少了后续处理中需要处理的数据量。
假设有三个像素点A、B、C,它们的梯度方向都是从左到右(水平方向)。梯度值分别为:
- A点:梯度值最大
- B点:梯度值较小
- C点:梯度值较小
根据非极大值抑制的原则,只保留梯度值最大的A点,而将B点和C点的梯度值置为0,因为它们不是局部最大值。
3.4 用双阈值算法检测和连接边缘
-
设置阈值:
- 高阈值(maxVal):用于确定强边缘,这个值应该设置得足够高,以确保只有真正强烈的边缘响应被标记为强边缘。
- 低阈值(minVal):用于确定弱边缘,这个值通常设置为高阈值的一半(即maxVal:minVal = 2:1),但也可以基于梯度直方图或其他标准来动态确定。
-
标记边缘:
- 如果一个边缘点的梯度值大于或等于高阈值,则将其标记为强边缘。
- 如果一个边缘点的梯度值介于高阈值和低阈值之间,则将其标记为弱边缘。
- 如果一个边缘点的梯度值小于低阈值,则将其抑制,不视为边缘。
-
处理弱边缘:
- 对于标记为弱边缘的点,需要检查它们是否与强边缘相连。如果一个弱边缘点与强边缘点相邻(在8邻域或4邻域中),则认为这个弱边缘点也是边缘的一部分,将其保留。
- 如果弱边缘点不与任何强边缘点相连,则认为它是由于噪声产生的假边缘,将其抑制。
通过这种双阈值处理,Canny算法能够有效地区分和连接边缘点,同时抑制由于噪声产生的假边缘。这种方法确保了边缘的连续性和完整性,同时减少了误检率。
阈值的确定对于Canny算法的性能至关重要。高阈值的确定可以基于经验,也可以通过分析梯度直方图来自动确定。例如,可以取梯度直方图的前30%作为高阈值,这是一种常见的自适应阈值确定方法。
3.5 Python代码实现
在Python中,OpenCV 提供了函数 cv2.Canny()来实现 Canny 边缘检测。
cv2.Canny(image, threshold1, threshold2, edges=None, apertureSize=3, L2gradient=False)
参数:
- image:输入图像,通常是灰度图像。
- threshold1:第一个阈值,用于边缘检测的低阈值。边缘强度低于此值的像素会被抑制。
- threshold2:第二个阈值,用于边缘检测的高阈值。边缘强度高于此值的像素会被认为是边缘。
- edges:输出图像,可以设置为 None,表示在函数内部分配内存。
- apertureSize:Sobel 算子的大小,默认为 3,必须是奇数。用于计算图像梯度。
- L2gradient:布尔值,表示是否使用更精确的 L2 范数来计算图像梯度。如果为 True,则使用 L2 范数;如果为 False,则使用 L1 范数(默认)。
# -*- coding: utf-8 -*-
import cv2
import numpy as np
img = cv2.imread('../1.jpg', cv2.IMREAD_GRAYSCALE)
canny = cv2.Canny(img, 100, 200)
cv2.imshow('canny', canny)
cv2.waitKey(0)
cv2.destroyAllWindows()
3.6 C++代码实现
int main()
{
cv::Mat image = cv::imread("../1.jpg", cv::IMREAD_GRAYSCALE);
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
cv::Mat canny;
cv::Canny(image, canny, 100, 200);
cv::imshow("canny", canny);
cv::waitKey(0);
cv::destroyAllWindows();
}
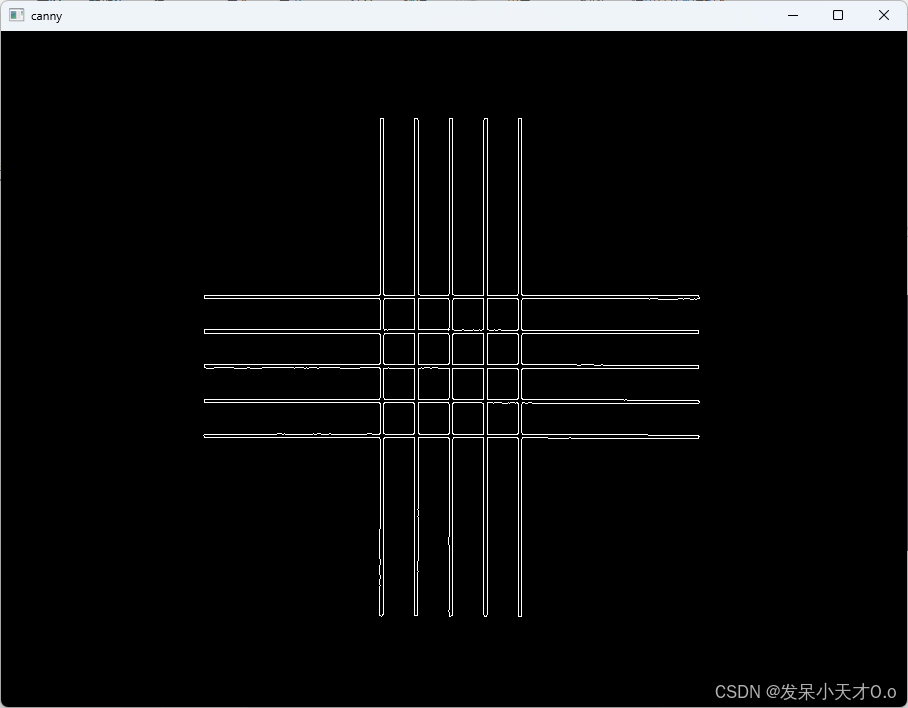
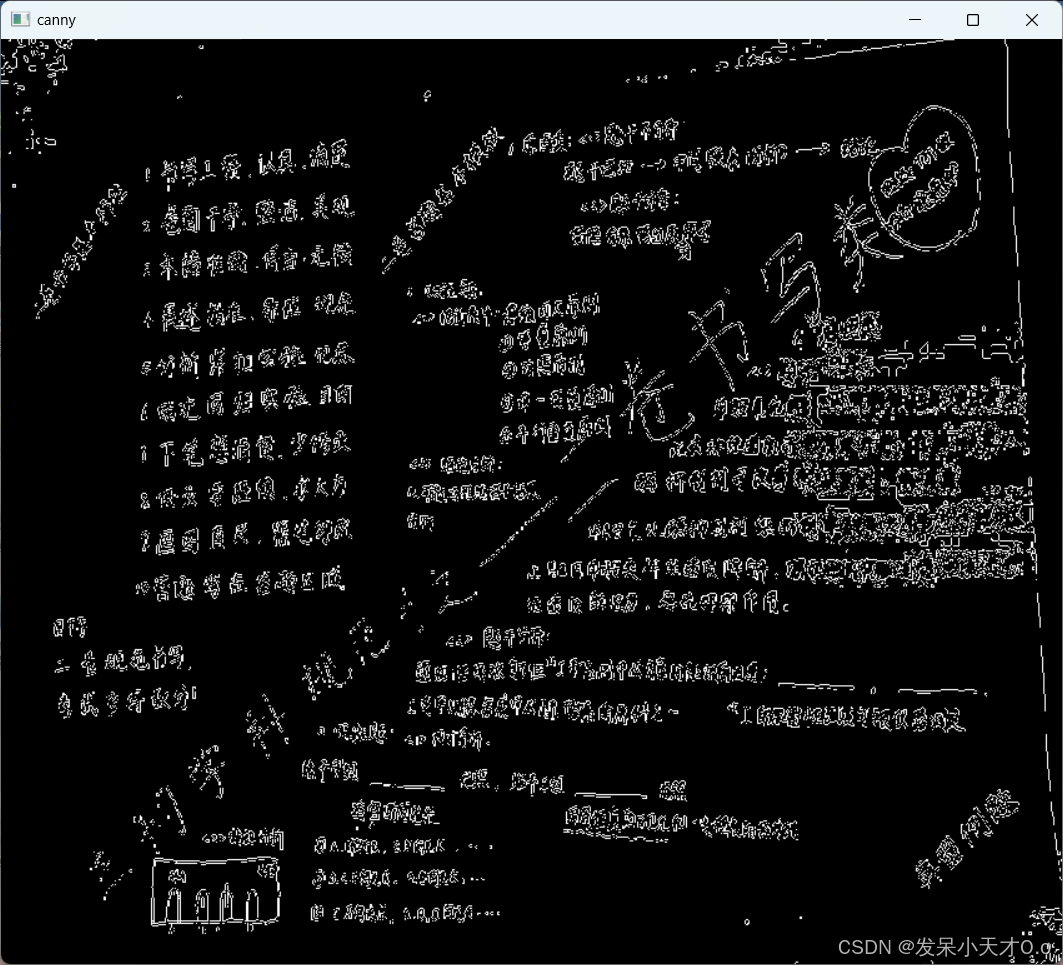
3.7 实现效果
4.轮廓提取
4.1 原理与过程
轮廓提取(Contour Extraction)是图像处理中常用的一项技术,主要用于从二值图像中提取物体的边界或轮廓。轮廓表示了物体的形状边界,可以是闭合的或开口的,通常由边缘或亮度变化显著的区域组成。
简单来说,边缘是图像中亮度变化剧烈的地方,比如从亮的区域到暗的区域的分界线。边缘检测就是通过找出这些变化来找到图像的边界。但问题是,边缘检测出来的边缘常常是断断续续的,不是一个完整的线。
而轮廓是由一系列连贯的边缘点组成的闭合曲线,代表了物体的外形。轮廓提取的目的是将这些零散的边缘连接起来,形成一个完整的物体边界。轮廓帮助我们更好地理解物体的整体形状,而边缘更多是作为物体的局部特征来使用。所以,边缘是识别物体的"分界线",而轮廓是物体的"完整外形"。
过程步骤:
1、图像预处理:
灰度化:首先将彩色图像转为灰度图,因为轮廓和边缘检测不依赖于颜色信息。
二值化:应用阈值化操作将图像转换为黑白图像(像素不是0就是255)。
应用边缘检测:可以使用 Canny 边缘检测来进一步增强图像中的边缘信息。Canny 算法能检测到图像中显著的亮度变化,从而有效地识别边缘。
可以应用二值化或边缘检测的其中一个,也可以两个都应用。
cv::threshold 用于图像二值化(即将图像转化为黑白图像),它将灰度图像中每个像素的值与指定阈值进行比较,将其分为前景和背景。通将像素值高于该值的区域设为白色(255),低于该值的区域设为黑色(0)。
double cv::threshold(
cv::InputArray src, // 输入图像
cv::OutputArray dst, // 输出图像
double thresh, // 阈值
double maxVal, // 最大值
int type // 阈值化类型
);
参数:
- src:输入图像,应该是灰度图像(单通道),即 CV_8U、CV_16U 或 CV_32F 类型的图像。
- dst:输出图像,与输入图像具有相同的大小和类型,但经过二值化处理。
- thresh:阈值,用于区分像素的高低值。所有像素值大于此阈值的区域将被设置为 maxVal,其余区域被设置为 0(黑色)。通常设置为127。Otsu 方法下该值设为 0,由算法自动计算合适的阈值。
- maxVal:大于阈值的像素将被赋予的最大值,通常设置为 255,即白色。
- type:阈值化类型,指定如何处理图像中的像素。可以是以下几种类型:
- cv::THRESH_BINARY:二值化,如果像素值大于 thresh,则设置为 maxVal,否则设置为 0。
- cv::THRESH_BINARY_INV:反转二值化,如果像素值大于 thresh,则设置为 0,否则设置为 maxVal。
- cv::THRESH_TRUNC:截断,所有大于 thresh 的像素值被截断为 thresh。
- cv::THRESH_TOZERO:保留大于 thresh 的像素值,其余像素设置为 0。
- cv::THRESH_TOZERO_INV:与 THRESH_TOZERO 相反,保留小于 thresh 的像素值,其他设置为 0。
- cv::THRESH_OTSU:Otsu 自适应阈值,自动计算最佳的阈值(需要灰度图像)。
每个像素根据阈值处理后得到的二值化图像(或其他类型的阈值图像,取决于 type 参数)。
注意: 在Python中,使用cv2.threshold 会返回两个值:
-
retval:实际使用的阈值。
如果使用 Otsu’s 方法(如 cv2.THRESH_OTSU),则该值是 Otsu 算法自动计算的最佳阈值。
否则,这个值与传入的 thresh 参数相同。 -
thresholded_image:经过阈值处理的图像。
retval, thresholded_image = cv2.threshold(src, 127, 255, cv2.THRESH_BINARY)
2、轮廓查找:
使用 cv::findContours 函数,输入二值图像,提取轮廓。这个函数通过遍历图像的边缘像素,识别并形成一个完整的轮廓。边缘可能是不连续,可以是一个点。而轮廓是将边缘点连接起来,是连续的。
int cv::findContours(
cv::Mat& image, // 输入图像,通常是二值图像
std::vector<std::vector<cv::Point>>& contours, // 输出的轮廓集合
cv::Mat& hierarchy, // 输出的轮廓层级结构
int mode, // 轮廓检索模式
int method // 轮廓近似方法
);
参数:
- image:输入图像,通常是二值图像,表示图像的前景与背景,轮廓是从前景中提取的。
- contours:一个向量,存储提取的轮廓,每个轮廓是一个点集。
- hierarchy:轮廓的层级关系(对于嵌套轮廓很有用)。
- mode:轮廓检索模式,常见值有:
cv::RETR_EXTERNAL:只检测最外层轮廓。
cv::RETR_LIST:检测所有轮廓,并将它们放在同一层级。
cv::RETR_TREE:检测所有轮廓,并建立完整的轮廓层级树。 - method:轮廓近似方法,常见值有:
cv::CHAIN_APPROX_SIMPLE:存储轮廓的端点。
cv::CHAIN_APPROX_NONE:存储轮廓的所有点。
3、轮廓近似(可选):
如果轮廓过于复杂,可以使用 cv::approxPolyDP 函数对轮廓进行多边形近似,减少轮廓中的点数量,去除冗余的轮廓点,简化轮廓表示。
void cv::approxPolyDP(
const std::vector<cv::Point>& curve, // 输入的轮廓或曲线(点集)
std::vector<cv::Point>& approxCurve, // 输出的多边形逼近后的点集
double epsilon, // 逼近精度(容忍度)
bool closed // 是否闭合(轮廓是否封闭)
);
参数:
- curve:输入的轮廓或曲线。它通常是一个 std::vector<cv::Point> 类型的数组,表示轮廓中的所有点。
- approxCurve:输出的逼近结果,表示逼近后的多边形的点集,也是一个 std::vector<cv::Point> 类型的数组。
- epsilon:逼近精度,控制逼近的精细度。它表示每个点与逼近多边形之间的最大距离。较小的 epsilon 值会保持更多的轮廓细节,而较大的 epsilon 值会导致更多的点被简化。
- closed:布尔值,表示轮廓是否闭合。如果是 true,表示逼近的轮廓是闭合的(即第一个点和最后一个点相连);如果是 false,则表示不闭合。
4、绘制轮廓:
使用 cv::drawContours 函数将轮廓绘制到图像上,可以选择绘制所有轮廓或某个特定轮廓。
void cv::drawContours(cv::InputOutputArray img,
const std::vector<std::vector<cv::Point>>& contours,
int contourIdx,
const cv::Scalar& color,
int thickness = 1,
int lineType = 8,
int hierarchy = 0,
int maxLevel = INT_MAX);
参数:
- img: 输入输出的图像,函数将在该图像上绘制轮廓。
- contours: 轮廓的数组,类型为 std::vector<std::vector<cv::Point>>。每个轮廓都是一个点的集合。
- contourIdx: 指定绘制的轮廓索引。如果为 -1,则绘制所有轮廓。
- color: 轮廓颜色,类型为 cv::Scalar,通常是 BGR 格式。
- thickness: 线条的粗细,默认值为 1。可以设置为 cv::FILLED(-1) 以填充轮廓。
- lineType: 线条类型,默认是 8。可以设置为 cv::LINE_AA 来实现抗锯齿。
- hierarchy: 可选参数,用于处理层次结构。如果不需要层次结构,可以忽略。
- maxLevel: 可选参数,指定绘制的轮廓层次,默认为 INT_MAX,表示绘制所有层次。
4.2 Python代码实现
import cv2
import numpy as np
image = cv2.imread("../3.jpg")
if image is None:
print("Error: Could not open or find the image!")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 使用二值化或Canny边缘检测
_, thres = cv2.threshold(gray, 150, 255, cv2.THRESH_BINARY)
canny = cv2.Canny(thres, 80, 150)
# 查找轮廓
contours, hierarchy = cv2.findContours(canny, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# 在原图或空白图上绘制轮廓
cv2.drawContours(image, contours, -1, (0, 255, 0), 1)
cv2.namedWindow("gray", cv2.WINDOW_FREERATIO)
cv2.namedWindow("thres", cv2.WINDOW_FREERATIO)
cv2.namedWindow("canny", cv2.WINDOW_FREERATIO)
cv2.namedWindow("contours", cv2.WINDOW_FREERATIO)
cv2.imshow("gray", gray)
cv2.imshow("thres", thres)
cv2.imshow("canny", canny)
cv2.imshow("contours", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
4.3 C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("../3.jpg");
if (image.empty())
{
std::cerr << "Error: Could not open or find the image!" << std::endl;
return -1;
}
cv::Mat gray, thres, canny;
cv::cvtColor(image, gray, cv::COLOR_BGR2GRAY);
cv::threshold(gray, thres, 150, 255, cv::THRESH_BINARY);
cv::Canny(thres, canny, 80, 150);
// 查找轮廓
std::vector<std::vector<cv::Point>> contours;
cv::Mat hierarchy;
cv::findContours(canny, contours, hierarchy, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_SIMPLE);
cv::drawContours(image, contours, -1, cv::Scalar(0, 255, 0), 1);
cv::namedWindow("gray", cv::WINDOW_FREERATIO);
cv::namedWindow("thres", cv::WINDOW_FREERATIO);
cv::namedWindow("canny", cv::WINDOW_FREERATIO);
cv::namedWindow("contours", cv::WINDOW_FREERATIO);
cv::imshow("gray", gray);
cv::imshow("thres", thres);
cv::imshow("canny", canny);
cv::imshow("contours", image);
cv::waitKey(0);
cv::destroyAllWindows();
return 0;
}
4.4 实现效果
灰度图:
二值图:
边缘图:
轮廓图: