✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
⛄ 内容介绍
路径规划是机器人技术中的一个重要研究领域,它涉及到如何使机器人在给定的环境中找到最佳的路径以完成特定任务。在现实世界中,机器人通常需要在复杂的环境中导航,包括避开障碍物、优化行进距离和时间等。因此,路径规划算法的设计和优化对于机器人的智能导航至关重要。
在路径规划算法中,粒子群优化(Particle Swarm Optimization,PSO)是一种常用的方法。PSO算法是一种模拟自然界中鸟群或鱼群等群体行为的优化算法。它通过模拟粒子在搜索空间中的移动和交互,以找到全局最优解。在机器人路径规划中,PSO算法可以用来寻找机器人在给定环境中的最佳路径。
PSO算法的核心思想是通过模拟群体中粒子的行为来搜索最优解。每个粒子代表一个可能的解,并根据自身的经验和群体的经验来调整自己的位置。在路径规划中,每个粒子代表一条可能的路径,而每个粒子的位置代表路径上的各个节点。通过不断迭代和更新粒子的位置,PSO算法可以逐渐找到全局最优解,即机器人的最佳路径。
在机器人路径规划中,PSO算法的具体步骤如下:
- 初始化粒子群的位置和速度。位置表示路径上的节点,速度表示路径的方向和速度。
- 计算粒子群中每个粒子的适应度值。适应度值表示路径的优劣程度。
- 更新粒子的速度和位置。根据粒子自身的最佳位置和群体的最佳位置,调整粒子的速度和位置。
- 判断终止条件。如果达到了预设的终止条件,算法结束;否则返回第2步。
- 输出全局最优解,即机器人的最佳路径。
PSO算法在机器人路径规划中的应用具有许多优点。首先,它能够有效地搜索全局最优解,避免陷入局部最优解。其次,PSO算法具有较快的收敛速度,能够在较短的时间内找到最佳路径。此外,PSO算法对问题的约束条件较为灵活,适用于各种不同类型的路径规划问题。
然而,PSO算法也存在一些局限性。首先,PSO算法对初始参数的选择较为敏感,不同的参数选择可能导致不同的结果。其次,PSO算法在处理高维问题时可能会遇到维度灾难的问题,导致搜索效率下降。此外,PSO算法对问题的解空间分布较为敏感,如果解空间分布不均匀,可能会导致算法无法找到最佳路径。
综上所述,基于粒子群优化的机器人路径规划算法是一种有效的路径规划方法。它通过模拟群体行为来搜索最优解,能够在复杂环境中找到机器人的最佳路径。然而,PSO算法仍然存在一些局限性,需要在实际应用中进行进一步优化和改进。未来的研究可以探索如何结合其他优化算法和机器学习方法,进一步提高机器人路径规划的性能和效果。
室内环境栅格法建模步骤
1.栅格粒大小的选取
栅格的大小是个关键因素,栅格选的小,环境分辨率较大,环境信息存储量大,决策速度慢。
栅格选的大,环境分辨率较小,环境信息存储量小,决策速度快,但在密集障碍物环境中发现路径的能力较弱。
2.障碍物栅格确定
当机器人新进入一个环境时,它是不知道室内障碍物信息的,这就需要机器人能够遍历整个环境,检测障碍物的位置,并根据障碍物位置找到对应栅格地图中的序号值,并对相应的栅格值进行修改。自由栅格为不包含障碍物的栅格赋值为0,障碍物栅格为包含障碍物的栅格赋值为1.
3.未知环境的栅格地图的建立
通常把终点设置为一个不能到达的点,比如(-1,-1),同时机器人在寻路过程中遵循“下右上左”的原则,即机器人先向下行走,当机器人前方遇到障碍物时,机器人转向右走,遵循这样的规则,机器人最终可以搜索出所有的可行路径,并且机器人最终将返回起始点。
备注:在栅格地图上,有这么一条原则,障碍物的大小永远等于n个栅格的大小,不会出现半个栅格这样的情况。
目标函数设定
⛄ 核心代码
function drawPath(path,G,flag)
%%%%
xGrid=size(G,2);
drawShanGe(G,flag)
hold on
set(gca,'XtickLabel','')
set(gca,'YtickLabel','')
L=size(path,1);
Sx=path(1,1)-0.5;
Sy=path(1,2)-0.5;
plot(Sx,Sy,'ro','MarkerSize',5,'LineWidth',5); % 起点
for i=1:L-1
plot([path(i,2) path(i+1,2)]-0.5,[path(i,1) path(i+1,1)]-0.5,'k-','LineWidth',1.5,'markersize',10)
hold on
end
Ex=path(end,1)-0.5;
Ey=path(end,2)-0.5;
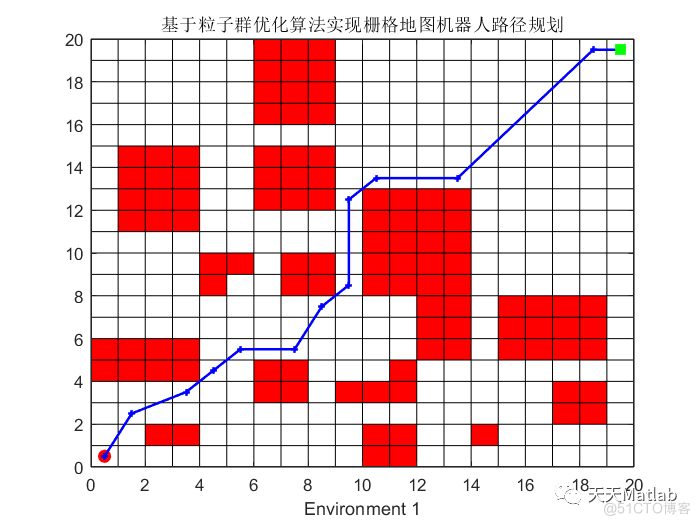
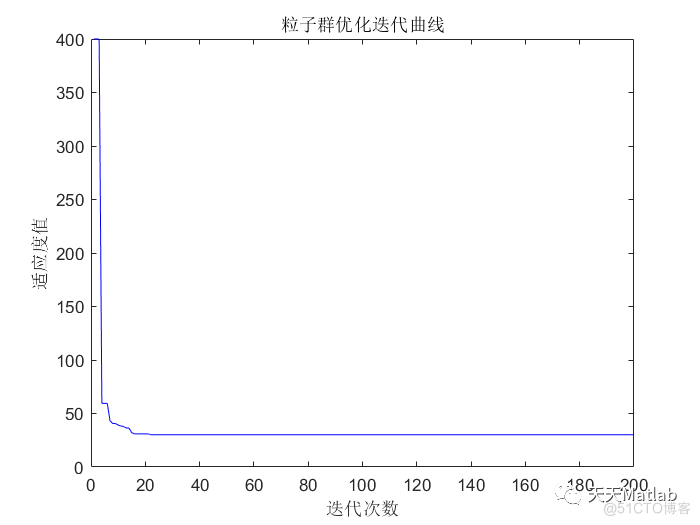
plot(Ex,Ey,'gs','MarkerSize',5,'LineWidth',5); % 终点⛄ 运行结果
⛄ 参考文献
[1] 张毅,刘杰.一种基于优化混合蚁群算法的机器人路径规划算法:CN201711121774.X[P].CN107917711A[2023-07-10].
[2] 吴宪祥,郭宝龙,王娟.基于粒子群三次样条优化的移动机器人路径规划算法[J].机器人, 2009, 31(6):5.DOI:10.3321/j.issn:1002-0446.2009.06.013.
[3] 崔鼎,郝南海,郭阳宽.基于RRT*改进的路径规划算法[J].机床与液压, 2020(9).