这学期在上《数字图像处理》这门课程,老师布置了几个大作业,自己和同学一起讨论完成后,感觉还挺有意思的,就想着把这个作业整理一下 :
1.实验任务和要求
实现“对比限制自适应直方图均衡化”(CLAHE)算法。对受大雾天气干扰的图片进行去雾增强处理(图片可网上搜索)。
2.实验原理与方法
首先是将原图像进行切割,本实验中采取了8x8的互不重叠分割区域。之后是进行每个小块的直方图统计,即统计每个像素值出现的频率。
将统计好的直方图进行对比度限制,CLAHE同普通的自适应直方图均衡不同的地方主要是其对比度限幅。这个特性也可以应用到全局直方图均衡化中,即构成所谓的限制对比度直方图均衡(CLHE),但这在实际中很少使用。在CLAHE中,对于每个小区域都必须使用对比度限幅。CLAHE主要是用来克服AHE的过度放大噪音的问题。这主要是通过限制AHE算法的对比提高程度来达到的。在指定的像素值周边的对比度放大主要是由变换函数的斜度决定的。这个斜度和领域的累积直方图的斜度成比例。CLAHE通过在计算CDF前用预先定义的阈值来裁剪直方图以达到限制放大幅度的目的。这限制了CDF的斜度因此,也限制了变换函数的斜度。直方图被裁剪的值,也就是所谓的裁剪限幅,取决于直方图的分布因此也取决于领域大小的取值。通常,直接忽略掉那些超出直方图裁剪限幅的部分是不好的,而应该将这些裁剪掉的部分均匀的分布到直方图的其他部分。如下图所示。
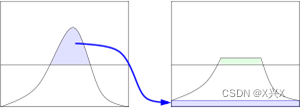
图2.1.1 直方图剪切原理
如上所述的自适应直方图,不管是否带有对比度限制,都需要对图像中的每个像素计算器领域直方图以及对应的变换函数,这使得算法及其耗时。
而插值使得上述算法效率上有极大的提升,并且质量上没有下降。首先,将图像均匀分成等份矩形大小,如下图的右侧部分所示(8行8列64个块是常用的选择)。然后计算个块的直方图、CDF以及对应的变换函数。这个变换函数对于块的中心像素(下图左侧部分的黑色小方块)是完全符合原始定义的。而其他的像素通过哪些于其临近的四个块的变换函数插值获取。位于图中蓝色阴影部分的像素采用双线性查插值,而位于便于边缘的(绿色阴影)部分采用线性插值,角点处(红色阴影处)直接使用块所在的变换函数。
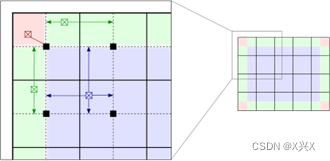
图2.1.2 插值原理图
插值过程中,将图像分成的小块分为三类,第一种是四个角上的小块,文献中使用CR代表每个角上的小块,第二种是边缘上的小块,用BR表示,第三种是中间的小块,用IR表示。
图2.1.3 插值小块分类
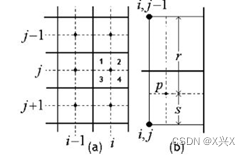
对于IR组中的区域,该区域的每个象限基于其四个最近相邻区域的映射进行映射,以(i,j)区域第一象限内的像素值为例,由相邻的竖直和水平四个小块进行映射,即(i, j),(i,j-1),(i-1,j),(i-1,j-1)计算公式如下。
公式2.1.4 IR区域像素值计算公式
其中各小块的位置示意图和元素的示意图如下图所示:
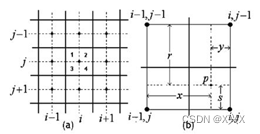
图2.1.4 (a)一个给定的IR区域及其所有相邻区域
(b)(i,j)区域象限1的像素p及其与四个最近区域中心的关系
对于BR组中的区域,该区域中的第一三象限内的小块的像素值计算方法和IR中的相同,但是其二四象限内的小块的计算方法如下公式:
公式2.1.5 BR区域二四象限像素值计算公式
其中各小块的位置示意图和元素的示意图如下图所示:
图2.1.5 (a)给定的BR区域及其所有相邻区域
(b)(i,j)区域象限2的像素p及其与最近两个区域中心的关系
对于CR组的区域,不同象限具有不同的特征。该组中的一个典型区域,左上角,如下图所示。关于IR和BR组的讨论,象限4具有与IR区域相似的邻域结构,象限2和3具有邻域结构。类似于BR区域两侧象限的结构。象限1在该组中是唯一的,与其他区域没有联系。该象限中像素的映射函数与区域映射相同,不考虑其他区域。在这种情况下,映射如下公式所示:
公式2.1.6 CR区域一象限像素值计算公式
图2.1.6 给定的CR区域及其所有相邻区域
综上所述,本实验的步骤如下流程图所示,分别是先对图像进行分割,再通过循环计算每个小块的直方图,进行对比度限制,再根据小块的种类进行插值处理。
3.实验代码
本次实验的数据集采集自网络上搜索的带有大雾条件干扰的图片。
数据集:
#1.先把图像分块 2.统计直方图 3.每块进行CLAHE 4把分块的图像合并 5.双线性插值处理边缘 6.显示图像
import cv2
import numpy as np
import matplotlib.pyplot as plt
#img=cv2.imread("F:\BaiduNetdiskDownload\pictures\senlin.png")
#img=cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
#h,s,v=cv2.split(img)
#print(v)
################################################
#对图像进行边界填充
def copymakeborder(image,m,n):
'''
对图像进行边界填充
:param image:
:param a:
:param b:
:return:
'''
image = cv2.copyMakeBorder(image, 0, m - image.shape[0] % m, 0, n - image.shape[1] % n, cv2.BORDER_REPLICATE)
# cv2.copyMakeBorder(src,top,bottom,left,right,borderType,value)
# src:原图像;top:顶部填充的像素行数;bottom:底部填充的像素行数;left:左边填充的像素列数;right:右边填充的像素列数;borderType:边界类型;value:一个可选参数
return image
#h=copymakeborder(h,8,8);s=copymakeborder(s,8,8)
#单独对v通道进行图像分块 v:M*N
def imagesplit(image,m,n,max):
'''
把图像分成a*b个小块
:param a:
:param b:
:return:
'''
image=copymakeborder(image,m,n) #填充边界,该函数在上面有定义
h=image.shape[0]
w=image.shape[1]
grid_h=int(h/m) #每个网格的高
grid_w=int(w/n) #每个网格的宽
# image_split=np.zeros(image.shape,np.uint8) #创建空的数组
lut=[]
cnt=1
for i in range(m):
for j in range(n):
x,y=int(grid_w*j),int(grid_h*i)
patch=image[y:y+grid_h,x:x+grid_w]
patch_1=histogram_statistics(patch) #统计直方图,该函数在下面有定义
patch_1=histogram_clahe(patch_1,max) #设置阈值重新分配直方图,该函数在下面有定义
hist_mapping_lst=hist_mapping(patch_1) #得到映射后的新的灰度级列表,该函数在下面有定义
''' #把映射后的值填充进每个小块中
for p in range(grid_h):
for q in range(grid_w):
patch[p][q]=hist_mapping_lst[patch[p][q]]
'''
lut.append(hist_mapping_lst)
cnt+=1
# cv2.imshow('%d'%cnt+'.jpg',patch)
# image_split[y:y+grid_h,x:x+grid_w]=patch #映射之后的总的图像
image=image_interpolation_new(image,m,n,lut) #遵循获取的新的灰度级列表,对整个大图像进行插值处理,目的是消除每个小块之间的块状效应,使图像看起来更平滑
return image
#####################################################################
#调试程序
'''
cv2.imshow('v image',v)
image_split=imagesplit(v,8,8)
cv2.imshow('final image',image_split)
'''
#######################################################################
#对每一个小块进行直方图统计
def histogram_statistics(image):
'''
进行直方图统计
:return:
'''
his_sta=plt.hist(image.ravel(),256,[0,256])
return his_sta
#######################################################################
#设置阈值,重新分配直方图
def histogram_clahe(hist,max):
'''
设置阈值,进行直方图的重新分配
:param hist:
:return:
'''
sum=0
for i in range(len(hist[0])):
if hist[0][i] > max:
sum+=(hist[0][i]-max)
for i in range(len(hist[0])):
hist[0][i] += sum//len(hist[0])
return hist
#####################################################
#灰度级映射函数
def hist_mapping(hist):
'''
0-256的灰度级映射
:param hist:
:return:
'''
hist_mapping_lst=[]
sum=0
for i in range(len(hist[0])):
sum+=hist[0][i] ###也可以直接用sum=hist[0].sum()函数来计算
sum_1=0
for j in range(len(hist[0])): #如果直接用for j in hist[1]: 的话,会显示索引256超出范围
sum_1 += hist[0][j]
Sk = (len(hist[0]) - 1) * sum_1 // sum
hist_mapping_lst.append(Sk)
'''
if Sk==Sk: #判断是否为空,若不为空,则运行下面的语句
hist_mapping_lst.append(int(Sk))
else:
hist_mapping_lst.append(0) #消除空值项,若为空值则填0
'''
return hist_mapping_lst
#############################################################################
#新的插值函数
def image_interpolation_new(image,m,n,lut):
"""
分区域对图像进行插值
:param image:
:return:
"""
image_h=image.shape[0]
image_w=image.shape[1]
h=image_h/m
w=image_w/n
for i in range(image_w):
for j in range(image_h):
# 四个角落
if i <= w/2 and j <= h/2: #左上角的块
image[j][i]=lut[0][image[j][i]]
elif i >= (image_w-w/2) and j <=h /2: #右上角的块
image[j][i]=lut[n-1][image[j][i]]
elif i >= (image_w-w/2) and j >= (image_h-h/2): #右下角的块
image[j][i]=lut[m*n-1][image[j][i]]
elif i <= (w/2) and j >= (image_h-h/2): #左下角的块
image[j][i]=lut[m*n-8][image[j][i]]
# 四个边缘除了角落的区域
elif j<=(h/2): #上部的边缘
if (i%w-w/2)>0 and (j%h-h/2)<0: #第一象限
y=(i%w)-w/2
x=w-y
image[j][i]=int((y/(x+y))*lut[int(i//w+1)][image[j][i]])\
+int((x/(x+y))*lut[int(i//w)][image[j][i]])
if (i%w-w/2)<0 and (j%h-h/2)<0: #第二象限
y=w/2-(i%w)
x=w-y
image[j,i]=int((y/(x+y))*lut[int(i//w-1)][image[j][i]])\
+int((x/(x+y))*lut[int(i//w)][image[j][i]])
elif i>=(image_w-w/2): #右部的边缘
if (i%w-w/2)>0 and (j%h-h/2)<0: #第一象限
s=h/2-(j%h)
r=h-s
image[j][i]=int((s/(s+r))*lut[int((j//h-1)*n+(i//w))][image[j][i]])\
+int((r/(r+s))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)>0 and (j%h-h/2)>0: #第四象限
s=(j%h)-h/2
r=h-s
image[j,i]=int((s/(r+s))*lut[int((j//h+1)*n+(i//w))][image[j][i]])\
+int((r/(r+s))*lut[int((j//h)*n+(i//w))][image[j][i]])
elif j>=(image_h-h/2): #下部的边缘
if (i%w-w/2)<0 and (j%h-h/2)>0: #第三象限
y=w/2-(i%w)
x=w-y
image[j][i]=int((y/(x+y))*lut[int((j//h)*n+(i//w-1))][image[j][i]])\
+int((x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)>0 and (j%h-h/2)>0: #第四象限
y=(i%w)-w/2
x=w-y
image[j,i]=int((y/(x+y))*lut[int((j//h)*n+(i//w+1))][image[j][i]])\
+int((x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
elif i<=(w/2): #左部的边缘
if (i%w-w/2)<0 and (j%h-h/2)<0: #第二象限
s=h/2-(j%h)
r=h-s
image[j][i]=int((s/(r+s))*lut[int((j//h-1)*n+(i//w))][image[j][i]])\
+int((r/(r+s))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)<0 and (j%h-h/2)>0: #第三象限
s=(j%h)-h/2
r=h-s
image[j][i]=int((s/(r+s))*lut[int((j//h+1)*n+(i//w))][image[j][i]])\
+int((r/(r+s))*lut[int((j//h)*n+(i//w))][image[j][i]])
# 中心区域
else:
if (i%w-w/2)>0 and (j%h-h/2)<0: #第一象限
s=h/2-(j%h)
r=h-s
y=(i%w)-w/2
x=w-y
image[j,i]=(s/(r+s))*((y/(x+y))*lut[int((j//h-1)*n+(i//w+1))][image[j][i]]+(x/(x+y))*lut[int((j//h-1)*n+(i//w))][image[j][i]])\
+(r/(r+s))*((y/(x+y))*lut[int((j//h)*n+(i//w+1))][image[j][i]]+(x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)<0 and (j%h-h/2)<0: #第二象限
s=h/2-(j%h)
r=h-s
y=w/2-(i%w)
x=w-y
image[j,i]=(s/(r+s))*((y/(x+y))*lut[int((j//h-1)*n+(i//w-1))][image[j][i]]+(x/(x+y))*lut[int((j//h-1)*n+(i//w))][image[j][i]])\
+(r/(r+s))*((y/(x+y))*lut[int((j//h)*n+(i//w-1))][image[j][i]]+(x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)<0 and (j%h-h/2)>0: #第三象限
s=(j%h)-h/2
r=h-s
y=w/2-(i%w)
x=w-y
image[j,i]=(s/(r+s))*((y/(x+y))*lut[int((j//h+1)*n+(i//w-1))][image[j][i]]+(x/(x+y))*lut[int((j//h+1)*n+(i//w))][image[j][i]])\
+(r/(r+s))*((y/(x+y))*lut[int((j//h)*n+(i//w-1))][image[j][i]]+(x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
if (i%w-w/2)>0 and (j%h-h/2)>0: #第四象限
s=(j%h)-h/2
r=h-s
y=(i%w)-w/2
x=w-y
image[j,i]=(s/(r+s))*((y/(x+y))*lut[int((j//h+1)*n+(i//w+1))][image[j][i]]+(x/(x+y))*lut[int((j//h+1)*n+(i//w))][image[j][i]])\
+(r/(r+s))*((y/(x+y))*lut[int((j//h)*n+(i//w+1))][image[j][i]]+(x/(x+y))*lut[int((j//h)*n+(i//w))][image[j][i]])
return image
###################################################################
#定义总的clahe函数
def clahe(img,m,n,max):
'''
总的clahe函数
:param image:
:param h:
:param s:
:param m:
:param n:
:param max:
:return:
'''
img = cv2.cvtColor(img, cv2.COLOR_BGR2HSV) #BGR转HSV通道
h, s, v = cv2.split(img) #分离为h,s,v三通道
v=imagesplit(v,m,n,max) #单独对v通道进行处理(包含扩充v通道图像)
h=copymakeborder(h,m,n) #扩充h图像的边界
s=copymakeborder(s,m,n) #扩充v图像的边界
img = cv2.merge([h, s, v]) #合并h,s,v图像
img = cv2.cvtColor(img, cv2.COLOR_HSV2BGR) #HSV转BGR通道
return img
##################################################################
###################################################################
img=cv2.imread("F:\BaiduNetdiskDownload\pictures\yulin\yulin.jpg")
img=clahe(img,8,8,8)
cv2.imshow('img\'s final image',img)
k=cv2.waitKey(0)
if k==ord('s'):
#cv2.imwrite('F:\BaiduNetdiskDownload\pictures\yulin\ final.jpg',img)
cv2.destroyAllWindows()本实验的难点在于图像的插值处理,具体原理可参照第二节实验原理部分;
需要注意的是,插值处理中,是根据按照阈值重新分配后得到的灰度级列表来重新赋值的,也就是用原先图像中的像素值作为索引,去寻找重新分配后相应的灰度级列表里新的像素值,赋值即可
结果:




以OpenCv库里的“createCLAHE”函数作为基准算法,依次输入图像,得到的结果图像如下:
import cv2 as cv
path = 'F:\BaiduNetdiskDownload\pictures\yulin\yulin.jpg'
img = cv.imread(path, cv.IMREAD_COLOR)
# print(img)
# 拆分通道
b, g, r = cv.split(img)
# CLAHE 对比限制自适应直方图均衡化 clipLimit:对比度限制值,默认为40.0;tileGridSize:分块大小,默认为Size(8, 8)
clahe = cv.createCLAHE(clipLimit=2.5, tileGridSize=(8, 8))
# print(clahe)
b = clahe.apply(b)
g = clahe.apply(g)
r = clahe.apply(r)
# 合并通道
img = cv.merge([b, g, r])
cv.imshow("img", img)
k=cv.waitKey(0)
if k==ord('s'):
cv.imwrite('F:\BaiduNetdiskDownload\pictures\yulin\ final.jpg', img, [cv.IMWRITE_JPEG_QUALITY, 50])
cv.destroyAllWindows()

可以看到,OpenCv库里的“createCLAHE”函数,其去雾效果是比较好的,对于处理完成后的整个图像,其整体平滑性非常好,不存在图像的分块现象,而且在运行过程中,其速度非常快,远快于自己编写的算法程序;
但是也可以看到,由于“基准算法”是对图像的BGR三通道分别进行处理,其处理的图a和图d,存在着颜色的失真现象;而自己编写的程序,是先把BGR三通道转化为HSV三通道,再单独对V通道图像进行处理,之后再合并HSV三个通道的图像,最后再转化为BGR通道图像,对于图a和图d,不会存在明显的失真现象。