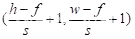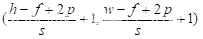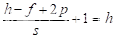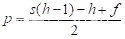文章目录
前言
这篇记录下CV入门的图像基础
一、直方图
1.基本概念
1)定义:
图像的灰度直方图描述了图像中灰度分布情况,可以很直观的展示出图像中各个灰度级所占的多少。其中,横坐标是灰度级,纵坐标是对应灰度像素出现的频率。
2)性质:
①:图像直方图描述每个灰度级具有的像素个数。
②:图像直方图不关心像素所处的空间位置,因此不受图像旋转和平移变化的影响,可作为图像的特征。
③:任何一幅特定的图像都有唯一的直方图与之对应,但不同的图像可以有相同的直方图。
④:若一个图像有两个不相连的区域组成,并且每个区域的直方图已知,则整幅图像的直方图是该两个区域的直方图之和。
⑤:多通道直方图:n通道则会在图上有n条曲线。正常图像的直方图分布应符合正态分布。
2.直方图均衡化
1)定义:
将原图像的直方图通过变换函数变为均匀的直方图,然后按均匀直方图修改原图像,从而获得一幅灰度分布均匀的新图像。
换言之:将直方图不规则分布的图像改为均匀分布的图像,是图像更加合理自然。
2)作用:
图像增强。
3)原理:
为了将原图像的亮度范围进行扩展,需要一个映射函数,将原图像的像素值均衡映射到新直方图中,这个映射函数有两个条件:
①:为了不打乱原有的顺序,映射后亮、暗的大小关系不能改变。
②:映射后必须在原有的范围之内。
4)具体过程:
①:依次扫描原始灰度图像的每一个像素,计算出图像的灰度直方图H。
②:计算灰度直方图的累加直方图
③:根据累加直方图和直方图均衡化原理得到输入与输出之间的映射关系。
④:最后根据映射关系得到结果:dst(x,y)=H’(SRC(x,y))进行图像变换。
p, q表示同一个像素经过映射之后,从p灰度级转到了q
可参考博客:https://blog.csdn.net/schwein_van/article/details/84336633
二、滤波和卷积
1.滤波
1)计算:
对位相乘,加权求和。
2.卷积
1)计算:
卷积核与图像对应位置的乘积和。
2)卷积和滤波的区别:
二者卷积核为翻转180°。
在单独做卷积时,不需要翻转,但从卷积到滤波或者是从滤波到卷积时需要翻转180°。
3)卷积核/过滤器/Kernel:
①:滤波器的大小应该为奇数,这样才有中心。
②:滤波器矩阵的所有元素之和应该要=1,目的:为了保证滤波前后图像亮度保持不变,但不是硬性要求。当元素之和>1时,滤波后图像比原图像更亮,反之则更暗。
③:对于滤波后的结果,可能出现负数或者大于255的数值,此时应将负数取绝对值,大于255的数截断到255。
④:在具体应用中,往往有多个卷积核,可认为,每个卷积核代表了一种图像模式。
4)常见卷积核:
①:无任何效果的卷积核:将原像素中间值乘1,其余全部乘0,像素值不会发生任何变化。
②:平滑均值滤波:取九个值的平均值代替中间像素值—起到平滑效果。
③:高斯平滑:水平和垂直方向呈现高斯分布,更突出了中心点在像素平滑后的权重,相比于均值滤波而言有更好的平滑效果。
(不应该是14嘛)
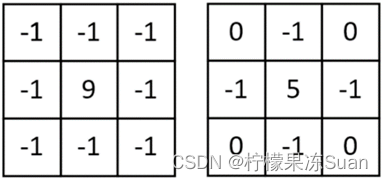
④:图像锐化:拉普拉斯变换核函数。
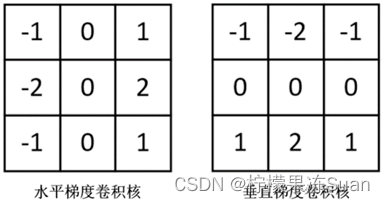
⑤:Soble边缘检测:更加强调了和边缘相邻的像素点对边缘的影响。
若既想检测水平又想检测竖直,可以将两个卷积核合并为一个。
卷积负责提取图像中的局部特征。
5)计算过程:
①:若用(f, f)的过滤器来卷积一张(h, w)大小的图片,每次移动s个像素,则输出为:
其中:f为过滤器的大小,h,w分别为图像的高和宽,s为步长。
存在问题:
1°:若f或s>1,则每次卷积之后结果的长宽会变小。
2°:丢失信息。
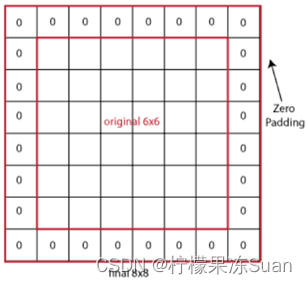
②:为了解决图像大小变化的问题,可以对图像进行填充,即在最外圈补0。
则输出图像大小变为:
若想高/宽不变,则有:
可得此时p应为:
注:当 不为整数时,取值向下取整。
向上取整:不管四舍五入的规则 只要后面有小数前面的整数就加1
向下取整:不管四舍五入的规则 只要后面有小数忽略小数
6)三种填充模式:
①:full:
从filter和image刚相交开始做卷积
②:same:
filter中心与image的边角重合时开始做卷积,是最常见的模式,可以在卷积过程中让图的大小保持不变。
③:valid:
filter全部在image里面时,进行卷积。
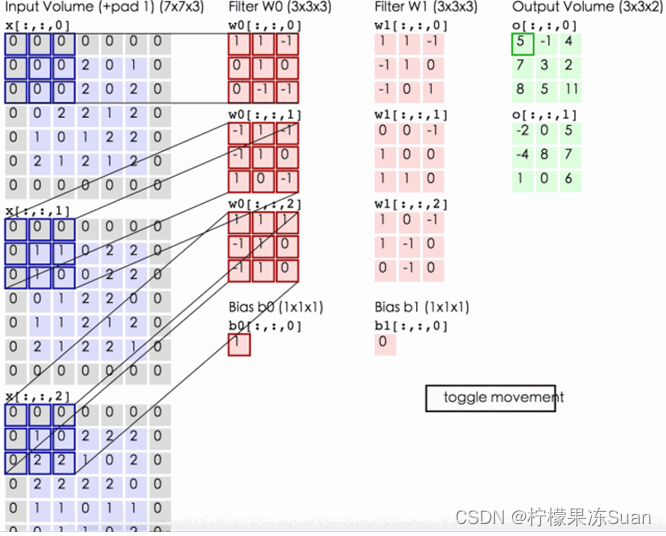
7)三通道卷积:
①:输入通道数 = 卷积核通道数
②:输出通道数 = 特征种类 = 卷积核个数
三、特征选择和提取
1.特征
1)定义:
在实际中,一个样本是用多个特征来表征的,即一个问题的影响因素可被称为特征。
2)特征分类:
①:相关特征:对学习任务有帮助,可以提升学习算法的效果。
②:无关特征:对算法没有任何帮助,不会给算法的效果带来任何提升。
③:冗余特征:未给算法带来新特征,或其特征信息可由其他特征推断出。
2.特征选择
1)目的:
a:降维,b:降低任务的难度,c:提升模型的效率。
2)定义:
从N个特征中选择其中M(M<=N)个子特征,并且在M个子特征中,准则函数可以达到最优解。
特征选择想要做的是:选择尽可能少的子特征,模型的效果不会显著下降,并且结果的类别分布尽可能的接近真实的类别分布。
3)特征选择过程:
①:生成过程:生成候选的特征子集,是一个搜索的过程。包含:
完全搜索:根据评价函数做完全搜索,主要有穷举搜索和非穷举搜索,
缺点:效率较低
启发式搜索:根据一些启发式规则在每次迭代时,决定剩下的特征是应该被选择还是被拒绝,这种方法简单且速度很快。
缺点:准确率低
随即搜索:随机搜索:每次迭代时会设置一些参数,参数的选择会影响特征选择的效果。
②:评价函数:评价特征子集的好坏,一个特征子集是最优的往往指相对于特征的评价函数来说的。
1°评价方法主要有三类:
过滤式:
包裹式:
嵌入式:
Filter和Wrapper组合式算法:
2°评价函数:
距离度量:
信息度量:
依赖度量:
一致性度量:
误分类率度量:
③:停止条件:用来决定迭代过程什么时候停止。停止条件包括:
达到预定的最大迭代次数。
达到预定的最大特征数。
增加(删除)任何特征不会产生更好的特征子集。
根据评价函数,产生最优特征子集
3.特征提取
1)常见特征:边缘、角、区域等。
提取目的:主要是为了排除信息量少的特征,减少计算量。
2)提取:是通过属性间的关系,如组合不同的属性得到新的属性,这样就改变了原来的特征空间。
选择:从原始特征数据集中选出子集,是一种包含关系,没有更改原始的特征空间。
二者都属于降维。
3)提取方法:
①:传统特征提取方法:基于图像本身的特征进行提取
②:深度学习方法:基于样本自动训练出区分图像的特征分类器。
四、PCA(主成分分析)算法
1.基本原理
1)原理:
将数据从原始的空间中转换到新的特征空间中,我们可以用新的坐标系来表示原始的数据,即(x, y, z)(a, b, c),组成新的特征空间,在新的特征空间中,可能所有的数据在某一维度上的投影都接近于0,则我们可以直接用(a, b)来表示数据,这样数据就从三维(x, y, z)降到了二维的(a, b)。
2)新基底的推导过程:
①:对原始数据零均值化(中心化)
②:求协方差矩阵
③:对协方差矩阵求特征向量和特征值,这些特征向量组成了新的特征空间。
2.零均值化(中心化)
1)中心化即指变量减去它的均值,使均值为0。其实就是一个平移过程,平移之后使得所有数据中心是(0, 0)。
中心化的几何意义:将样本集的中心平移到坐标系的原点O上。
2)降维目标:找到一个超平面,它能使得数据点的分布方差呈最大,这样数据表现在新坐标轴上的时候已经足够分散了。
3)方差:表示随机变量x与 的偏离程度,方差越大,说明数据越分散,则该属性能够比较好的反应源数据,若方差小或者为0,则样本在该特征方面几乎无差别。
4)PCA算法的优化目标就是:
①:降维后同一维度的方差最大。
②:不同维度之间的相关性为0。(若有相关性,则A可推导出B,则存在冗余特征)
面试提问:通过何种方法来实现不同维度相关性为0?
答:通过对协方差矩阵求特征值和特征向量
3.协方差
1)定义:是一种用来度量两个随机变量关系的统计量。同一元素的协方差即为该元素的方差,不同元素之间的协方差就表示它们的相关性。
2)物理意义:
当 时,表示X和Y正相关。
当 时,表示X和Y负相关。
当 时,表示X和Y不相关。所求目标….
4.协方差矩阵和向量求解
1)特点:
①:是计算不同维度之间的协方差,而不是不同样本之间的。
②:样本矩阵的每行是一个样本,每列是一个维度,所以我们要按列计算均值.
③:协方差矩阵的对角线就是个各个维度上的方差。
若做了中心化,则协方差矩阵为(中心化矩阵的协方差矩阵公式,m为样本个数)
2)对协方差矩阵求特征值、特征向量
①:过程略。
②:物理意义:对数字图像矩阵做特征值分解,其实是在提取这个图像中的特征,这些提取出来的特征是一个个向量,即对应着特征向量。而这些特征在图像中到底有多重要,特征重要性则通过特征值来表示。
③:对特征值进行排序:
1°:将特征值按照从大到小的排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵Wnxk。
2°计算XnewW,即将数据集Xnew投影到选取的特征向量上,这样就得到了我们需要的已经降维的数据集XnewW。
④:评价模型的好坏,k值的确定。
通过特征值的计算我们可以得到主成分所占的百分比,用来衡量模型的好坏。
5.优缺点:
1)优点:
①:完全无参数限制,在计算过程中完全不需要人为的设定参数或者是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
②:可以对数据进行降维,同时对新求出的“主元”向量的重要性进行排序,可达到降维从而简化模型或者是对数据进行压缩的效果,同时最大程度的保持了原有数据的信息。
③:各主成分之间正交,可消除原始数据成分之间的相互影响。
④:计算方法简单,易于在计算机上实现。
2)缺点:
①:若用户对观测对象有一定的先验知识,掌握了数据的一些特征,但是无法对该过程进行干预,得不到预期效果。
②:贡献率小的主成分往往可能含有对样本差异的重要信息,而这个方法却容易被忽略。
总结
人工智能CV算法入门第三篇,CV算法八股文,欢迎交流QQ:1395362556