【代码随想录】回溯算法

基本概念

回溯算法其实是递归算法。

回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。

并不是高效的算法，纯暴力搜索（for循环）。
可以解决哪类问题：

组合问题：给一个集合，在集合里找出大小为2的组合
切割问题：给一个字符串，问有几种切割的方式/怎样切割有多少回文字串
子集问题
排列问题（组合没有顺序，排列有顺序）
棋盘问题：N皇后，解数独

理解回溯法：

抽象成一个图（树）形结构：递归一定是有终止的。可以抽象成N叉树，树的宽度就是每个节点处理的集合大小，用for循环遍历。树的深度，用递归来处理。（很像层序遍历加上处理节点和回溯的操作）

回溯法模板：
伪代码

void backtracking(参数){
	if (终止条件){
		叶子节点-收集结果
		（只有子集问题每一个节点都要收集结果）
		return;
	# 单层搜索
	for (集合元素){
	处理节点；
	递归函数；
	回溯操作； # 撤销处理节点的情况
	}
	return;
	}
}

组合问题-77. 组合

回溯法三部曲：（和递归三部曲一模一样）

递归函数的返回值以及参数
回溯函数终止条件
单层搜索的过程

代码注意：定义backtracking需要传进self参数

剪枝条件：同一层中剩余元素数少于需要选取数n-(k-len(path)). len(path)是已经选取的数量。

组合问题-216.组合总和III

递归函数的返回值以及参数
回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要啥参数了，填什么参数。
确定终止条件
如果 len(path) 和 k 相等了，就终止。
如果此时path里收集到的元素和 sum 和 targetSum（就是题目描述的n）相同了，就用 result 收集当前的结果。
单层搜索过程
处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。
别忘了处理过程和回溯过程是一一对应的，处理有加，回溯就要有减！

剪枝条件：1) 已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉。2) 和回溯算法：组合问题再剪剪枝一样，for循环的范围也可以剪枝，i <= 9 - (k - path.size()) + 1 就可以了。

问题：时间复杂度为什么是O(n*2^n)？
——卡哥回复：组合问题不过是某个节点选或不选的问题，这是两种情况，有n个节点就是2^n.

代码注意：
1）在二维数组result中append path这个list的时候，要append(path[:]), 只append(path)的话，append的内容是空。
2）backtracking函数定义的时候，不需要写上传入的参数是int还是list之类的。

组合问题-17.电话号码的字母组合

自己想的：
1）终止条件：深度=len(digit)
2）单层搜索过程：广度先用for循环搜数字2-9，然后对应各自的字母

每个节点都在集合里面取字母，是解题的关键。

回溯三部曲：

确定回溯函数参数
首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。
再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。
确定终止条件
跟我想的一样，但我没写对，又用for循环起来了
确定单层遍历逻辑
本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而77. 组合和216.组合总和III 都是求同一个集合中的组合！

注意：输入1 * #按键等等异常情况

自己代码实现要注意的点：
1）十种方式拼接Python字符串
经典用到，以及本题用到：
2）在init中定义dic的时候，钱敏啊要记得加self.dic, 后面调用也要加self, 不然识别不出来是本类的变量

组合问题-39. 组合总和

candidates 中的数字可以无限制重复被选取。

回溯三部曲：

递归函数参数
- 全局变量
  result = []
  path = []
- 题目中给出的参数
  集合candidates
  目标值target
- path的和
- startIndex来控制for循环的起始位置
  ——对于组合问题，什么时候需要startIndex呢？
  - 如果是一个集合来求组合的话，就需要startIndex，例如：77.组合，216.组合总和III。
  - 如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合。
递归终止条件
- sum大于target
- sum等于target：此时需要收集result
单层搜索的逻辑
从startIndex开始，搜索candidates集合。
注意本题和77.组合、216.组合总和III 的一个区别是：本题元素为可重复选取的。

回溯代码框架：

void main(参数){
	参数初始化；
	backtracking(参数)
	return 结果
}
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    	（剪枝条件）； //符合则进入循环，否则return
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

自己的代码注意：
1）backtracking中的for循环要从startIndex开始，才不会形成同样的集合，只是元素换了位置而已——诶，这样是不是就是排序了。StartIndex的作用就是处理同一个集合中取元素重复受影响的问题

组合问题-40.组合总和II

背回溯算法框架：

def main(self, 参数)：
	result = []
	path = []
	self.backtracking(参数)
	return result

def backtracking(self, 参数)：
	（剪枝条件）
	终止条件
	for i in 本层集合元素（树中节点孩子节点的个数）：
		处理节点
		self.backtracking(参数)
		回溯，撤销处理结果

这道题目和 39.组合总和 有如下区别：

本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的，而39.组合总和是无重复元素的数组candidates

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。因此本题要附加一个要求：去重。
——我们要去重的是同一树层上**的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

强调一下，树层去重的话，需要对数组排序！ 这样才可以用上我们要用的去重方法：candidates[i-1]==candidates[i]的话，不向下回溯，直接本层下一个元素，continue.
本题看来，去重已经代替了剪枝。
去重方法：
- 记录used数组。

# used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
# used[i - 1] == false，说明同一树层candidates[i - 1]使用过
# 要对同一树层使用过的元素进行跳过
if candidates[i] == candidates[i - 1] and used[i-1] == 0:
    continue
# used[i-1] == 0 更简单写法： not used[i-1]

直接用startIndex来去重也是可以的，会有些难理解，但代码更简单容易记

# 要对同一树层使用过的元素进行跳过
# 对于相同的数字，只选择第一个未被使用的数字，跳过其他相同数字
# 即允许i = startIndex and candidates[i] == candidates[i - 1]的情况继续向下回溯
if i > startIndex and candidates[i] == candidates[i - 1]:
    continue

对比一下上面的4道同一集合组合问题。
| 77. 组合问题 | 给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。 |从左向右取，不再重复取|
|216. 组合总和III|找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。|
| 39. 组合总和 | 给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。 |
| 40.组合总和II | 给定一个可以有重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。 |
对比总结：77和216是一类题，39和40是一类题，这两类题虽然都是组合问题，但解决思路稍有区别，没必要太过比较。
和回溯法模板不同，本题将去重和终止条件都放在了for循环里面，而不是回溯函数刚开始的时候。——为什么？
下面的代码：

if sum(path) == target:
    result.append(path[:])
    # return

加了result要加这个return吗？——好像不加结果也差不多？模板是要加

切割问题-131.分割回文串

本题这涉及到两个关键问题：

切割问题，有不同的切割方式
判断回文

其实切割问题类似组合问题。所以切割问题，也可以抽象为一棵树形结构。递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。
回溯三部曲

递归函数参数
全局变量数组path存放切割后回文的子串，二维数组result存放结果集。（这两个参数可以放到函数参数里）
本题递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的。
递归函数终止条件
从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。
那么在代码里什么是切割线呢？
在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。

// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了

单层搜索的逻辑
来看看在递归循环中如何截取子串呢？
在for (int i = startIndex; i < s.size(); i++)循环中，我们定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。 index是上一层已经确定了的分割线，i是这一层试图寻找的新分割线。
首先判断这个子串是不是回文，如果是回文，就加入在path中，path用来记录切割过的回文子串。
本题还有细节，例如：切割过的地方不能重复切割所以递归函数需要传入i + 1。

判断回文子串
可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。——之前刷过。
优化
在于如何更高效的计算一个子字符串是否是回文字串。本题可以用动态规划这种算法, 高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤。
自己实现的代码错误点/笔记：

判断if self.isPalindrome(s[startIndex:i+1]): 不是len(s)，是i+1
双指针判断回文的循环方法有两种写法：
- for left in range(len(s)//2):
- while left < right:
Python三种判断回文的方法:
- 双指针
- 字符串前序=反序：反序写法——[::-1] ——最快
- 用all函数——all(s[i] == s[len(s) - 1 - i] for i in range(len(s) // 2))

切割问题-93.复原IP地址

与131.分割回文串类似。
回溯三部曲

递归参数
本题我们还需要一个变量pointNum，记录添加逗点的数量。
其实用python可以不需要，还按之前的path, 然后'.'.join(path)就可以了。
递归终止条件
终止条件和131.分割回文串情况就不同了，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。pointNum表示逗点数量，pointNum为3说明字符串分成了4段了。 然后验证一下第四段是否合法，如果合法就加入到结果集里
单层搜索的逻辑
在131.分割回文串中已经讲过在循环遍历中如何截取子串。
在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串，需要判断这个子串是否合法。
如果合法就在字符串后面加上符号.表示已经分割。
如果不合法就结束本层循环。
注意：
- 递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。
- 回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。

判断子串是否合法
主要考虑到如下三点：
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
代码错误：

s[i] > '9' or s[i] < '0' for i in range(len(s)):拼接了python和C++的写法，是不对的。
正确的Python写法：

for i in range(start, end + 1):
	if not s[i].isdigit():  # 遇到非数字字符不合法
		return False

检查段位以0为开头的数字
- 是str.startswith( 'this' )，不是startwith.
- 也可以用s[0] == '0'
检查段位如果大于255了不合法：int(s)可以直接把长字符串转换成整型，但如果s不合法的话，里面会有'.'，int(s)的时候会报错ValueError: invalid literal for int() with base 10。
解决方法：
- 转换单个的int(s[i])

num = 0
for i in range(start, end + 1):
    num = num * 10 + int(s[i])
    if num > 255:  # 如果大于255了不合法
        return False

num = int(s[start:end+1]) 总是会报错
- 主要原因还是s字符串切片出了问题。
- s[start:end+1]才能取到start到end索引内的内容，因为python字符串切片也是左闭右开的，for循环也是左闭右开的。
- 把start和end当成变量写出来可以防止出错
  References
python对字符串切片、split分割、截取数据
Python中字符串切片详解
python中字符截取[-1]、[:-1]、[::-1]、[n::-1]等使用方法的详细讲解（建议留存）

子集问题

如果把子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！历这个树的时候，把所有节点都记录下来，就是要求的子集集合。
其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和子集{2,1}是一样的。
那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！
什么时候for可以从0开始呢？
求排列问题的时候，for就要从0开始，因为集合是有序的。
回溯三部曲

递归函数参数
模板题，常规的startIndex, result, path
递归终止条件
剩余集合为空的时候，就是叶子节点。
单层搜索逻辑
求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

最快刷题记录：10分钟！

子集问题-90. 子集 II

这道题目和78.子集区别就是集合里有重复元素了，而且求取的子集要去重。
那么关于回溯算法中的去重问题，在40.组合总和II 中已经详细讲解过了，和本题是一个套路。
后期的排列问题里去重也是这个套路，所以理解“树层去重”和“树枝去重”非常重要。
代码基本跟组合差不多，只是需要注意去重的代码：

去重需要对数组排序
去重的几种方法：
- 利用used数组去重
- 利用集合useset去重
- 利用递归的时候下一个startIndex是i+1而不是0去重——要判断list[i]==list[i-1] and i > startIndex。（我常用）

代码出现的问题：

要加上i > startIndex，这样才是跳过树层重复而不是树枝重复

子集问题-491. 非递减子序列

在90.子集II中我们是通过排序，再加一个标记数组来达到去重的目的。
而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑！
回溯三部曲

递归函数参数
本题求子序列，很明显一个元素不能重复使用，所以需要startIndex，调整下一层递归的起始位置。
终止条件
本题其实类似求子集问题，也是要遍历树形结构找每一个节点，所以和回溯算法：求子集问题一样，可以不加终止条件，startIndex每次都会加1，并不会无限递归。
但本题收集结果有所不同，题目要求递增子序列大小至少为2。
单层搜索逻辑
同一父节点下的同层上使用过的元素就不能再使用了。

python去重方法：

利用set去重
利用哈希表去重

代码问题：

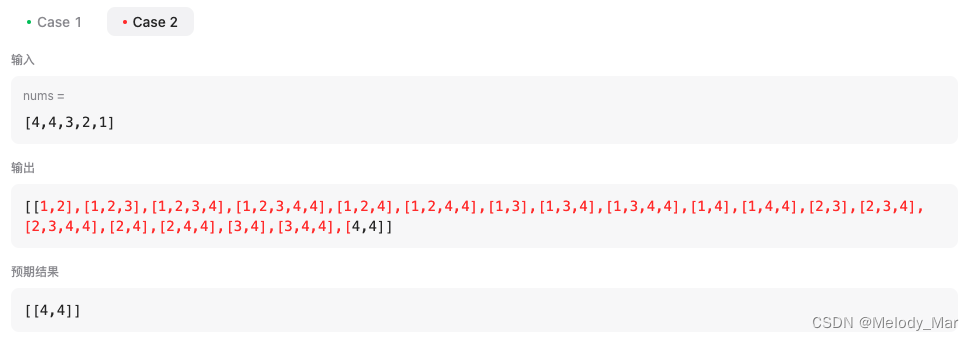
如果使用之前的逻辑——对数组排序，然后startIndex去重的话，case 2会出现下面的情况：

所以是不能用之前的去重逻辑的。
新的去重逻辑：
- 一开始用了判断if path and nums[i] < path[-1]，没用set的话，也会导致错误：
  
  因为这个用例里面，1最开始出现了一次，后面又出现了多次，如果用之前的i > startIndex and nums[i] == nums[i-1]这个去重逻辑，会导致检测不出来倒数第5个1导致的重复。因此还是要用set或哈希表来对原数组去重。一刷我就用set了。
- 去重的代码和前面判断递增的代码之间要用 or 连接，代表这里面任意一种情况出现都需要跳过：

if (path and nums[i] < path[-1]) or nums[i] in uset:
	continue

uset要在backtracking代码进入for循环之前初始化，这样才是记录本层去重。

排列问题-46. 全排列

不含重复数字，所以本题不涉及去重。
回溯三部曲

递归函数参数
首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
但排列问题需要一个used数组，标记已经选择的元素。
递归终止条件
可以看出叶子节点，就是收割结果的地方。
那么什么时候，算是到达叶子节点呢？
当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。
单层搜索的逻辑
这里和77.组合问题、131.切割问题和78.子集问题最大的不同就是for循环里不用startIndex了。
因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。
而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

代码实现时出现的问题：

used[i]进入本层递归是等于True，退出本层递归时，used[i]等于False。

排列问题-47.全排列 II

可包含重复数字的序列 nums，按任意顺序返回所有不重复的全排列。因此本题涉及去重。
**去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。**除非是题目的情况要求不能对元素排序。
代码实现时遇到的问题：

if 判断剪枝条件的时候used[i]需要用or和(i > 0 and nums[i] == nums[i-1] and used[i-1] == False) 并列判断：i每层都是从0开始的，只判断(i > 0 and nums[i] == nums[i-1] and used[i-1] == False)会导致树枝上面重复用到i=0的情况。上一题也是需要判断used[i]的，因此本题和上一题的区别就在于去重。used[i]需要记录已经使用过的元素。
这个判断条件要是不想用continue，可以对原来的判断条件取反：if not ((i > 0 and nums[i] == nums[i-1] and used[i-1] == 0) or used[i]):，或者是if (i = 0 or nums[i] != nums[i-1] or used[i-1] == True) and used[i] == False
在终止条件那里可以用result.apppend(path[:])，也可以用result.append(path.copy())。
由于要去重，一定要给nums排序：sorted(nums)

dfs函数里面的idx可以要，可以不要，不影响结果，因为已经for i in range(len(nums)了。
完整代码：

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:

        def dfs(idx, nums, path, result):
            if len(path) == len(nums):
                result.append(path[:])
                return
            
            for i in range(len(nums)):
                if (i == 0 or nums[i]!= nums[i-1] or used[i-1] == 1) and not used[i]:
                    path.append(nums[i])
                    used[i] = 1
                    dfs(idx+1, nums, path, result)
                    path.pop()
                    used[i] = 0

        path = []
        result = []
        used = [0] * len(nums)
        dfs(0, sorted(nums), path, result)
        return result

棋盘问题-51. N 皇后

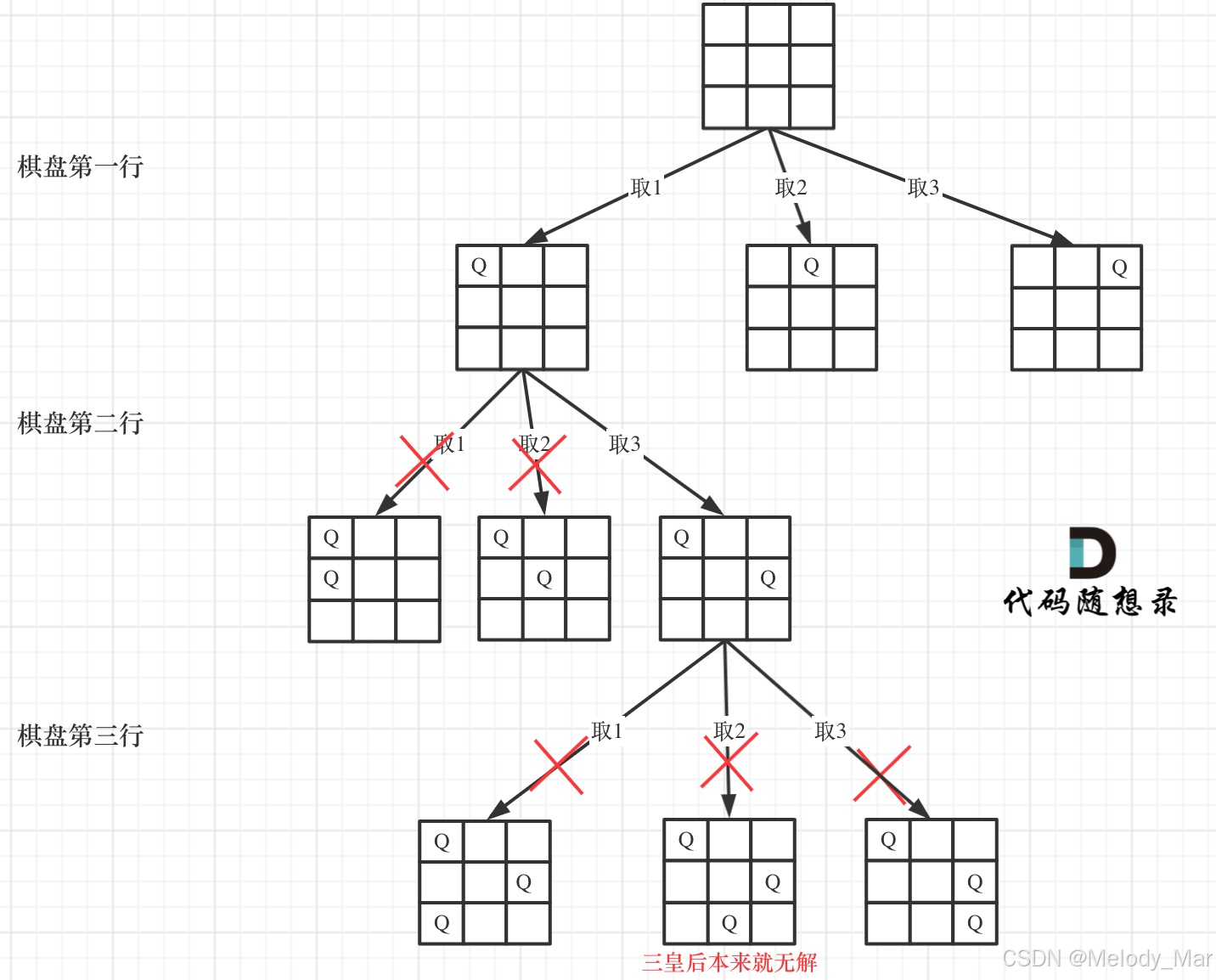
确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。
下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一棵树，如图：

在这里插入图片描述

从图中，可以看出，二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。

那么我们用皇后们的约束条件，来回溯搜索这棵树，只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了。

回溯三部曲：

递归函数参数
依然是定义全局变量二维数组result来记录最终结果。
参数n是棋盘的大小，然后用row来记录当前遍历到棋盘的第几层了。
递归终止条件
递归到棋盘最底层（也就是叶子节点）的时候，就可以收集结果并返回了。

单层搜索的逻辑
递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜，所以都是从0开始。

验证棋盘是否合法（这点和acwing的验证方法完全不同）
按照如下标准去重：
不能同行
不能同列
不能同斜线（45度和135度角）

def isValid(self, row: int, col: int, chessboard: List[str]) -> bool:
    # 检查列
    for i in range(row):
        if chessboard[i][col] == 'Q':
            return False  # 当前列已经存在皇后，不合法

    # 检查 45 度角是否有皇后
    i, j = row - 1, col - 1
    while i >= 0 and j >= 0:
        if chessboard[i][j] == 'Q':
            return False  # 左上方向已经存在皇后，不合法
        i -= 1
        j -= 1

    # 检查 135 度角是否有皇后
    i, j = row - 1, col + 1
    while i >= 0 and j < len(chessboard):
        if chessboard[i][j] == 'Q':
            return False  # 右上方向已经存在皇后，不合法
        i -= 1
        j += 1

    return True  # 当前位置合法

时间复杂度: $O (n!)$
空间复杂度: $O (n)$