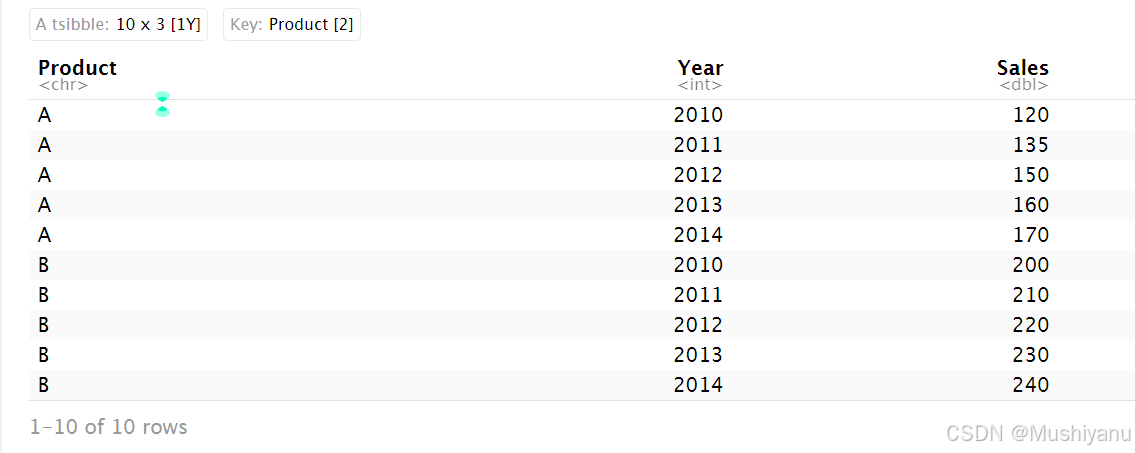• 本学习笔记任课参考老师的课件所制作，在此特别感谢我的老师。
• 本学习笔记参考北大李东风先生的《金融时间序列分析》授课备课资料，在此感谢。

时间序列变换和调整

在时间序列分析中，变换和调整帮助我们更准确地观察趋势、季节性和周期性，从而简化模型设计并提高其解释力。下面介绍四类常用方法：日历调整 、人口调整、通货膨胀调整和数学变换：

1. 日历调整
   日历因素会影响一些时间序列的数据，比如月度生产或销售数据，可能因每月天数的不同而波动。通过日历调整，例如用日均值或调整到季节性标准，可以去除这一影响，让数据反映真实的业务活动水平。

2. 人口调整
   在分析涉及人口规模的指标时，单看总量可能会误导我们。例如，在衡量某地教育资源时，如果只看学位数量而忽略适龄人口的变化，结论可能不准确。通过人均计算等方法可以更合理地评估资源的充裕程度和分布状态。

3. 通货膨胀调整
   经济数据在不同年份的对比需要考虑物价变化的影响。通过将数据按实际购买力进行通货膨胀调整（例如使用CPI调整），我们可以更客观地衡量实际的经济增长或收入变化，而不仅仅是名义上的数字增长。

4. 数学变换
   数学变换在时间序列分析中用于平稳化数据、降低波动，增强数据的可建模性。常见方法包括对数变换、差分、幂次变换等。对数变换能减少方差，适合处理指数增长序列；差分通过计算相邻数据的差值，去除趋势和季节性；幂次变换（如Box-Cox变换）调整数据分布，以更线性化的方式表示序列。通过这些变换，时间序列更易揭示内在模式，为进一步建模打下基础。

时间序列中的模式

在时间序列分析中，通过观察数据图表可以识别出一些常见的波动模式，这些模式通常分为以下几类：

1. 季节性 (Seasonal)
   季节性反映了数据中与特定时间段（如季节、月份）相关的规律性波动。例如，风扇的销量在夏季会增加而在冬季减少。这些周期性的、由季节变化引起的波动称为季节性，常记为 $S_t$。

2. 周期性 (Cyclic)
   周期性是指数据中不固定频率的上升和下降模式，如经济扩张和收缩的周期，其长度不固定，可能在3至10年之间。与季节性不同，周期性不具备固定的频率，常用于描述更长周期的波动。

3. 趋势 (Trend)
   趋势代表数据在较长时间内的平均水平变化，是一种较为长期的上升或下降趋势。例如，如果我们观察气温的变化，20年内的数据可能呈现出上升趋势，但如果有几百年的数据可能会显示更大的周期性。趋势常用 $T_t$ 表示，通常与周期性合并分析。

4. 假日效应 (Holiday Effect)
   假日效应或日历效应指特定日子或时间段内的特殊行为模式。例如，在金融市场中，周末效应是指最后一个交易日的表现不同于其他日的现象，这类特定时间的效应通常记为 $D_t$。

5. 非规则部分 (Irregular)
   非规则部分是指去除了趋势、周期和季节性后的随机波动部分。这一部分没有明显规律，通常被视为噪声或随机误差，记为 ${ϵ}_t$。

确定性因素分解

时间序列可以视为多种波动因素的叠加效果，其数学表达为：

$$X_t=f(T_t,S_t,D_t,{ϵ}_t)$$通常只考虑趋势性 $T_t$、季节性 $S_t$ 和非规则波动 ${ϵ}_t$，即简化为：
$$X_t=f(T_t,S_t,{ϵ}_t)$$时间序列分解就是将数据中的这些成分分离出来，使我们能够分别分析趋势和季节性变化，同时剔除随机波动的影响，从而帮助评估整体趋势并进行预测。

常见模型假设
时间序列分解依赖于函数 $f(\cdot )$ 的特定假设，主要有两种：

1. 加法模型：假设波动成分为简单相加的关系
   $$X_t=T_t+S_t+{ϵ}_t$$
2. 乘法模型：假设波动成分相互作用，为相乘关系$$X_t=T_t\cdot S_t\cdot {ϵ}_t$$ 由于乘法模型的形式可以通过对数变换转换为加法模型，便于分析，因此在实际应用中，常对乘法模型取对数，简化后续的分解和建模过程。

分析一个不含季节性的时间序列

在时间序列分析中，趋势被定义为“水平上的长期变化”。我们在此探讨如何估计趋势，这一过程称为趋势平滑（Trend Smoothing）。

假设时间序列模型为：
$$X_t=T_t+{ϵ}_t$$ 其中，$T_t$ 是时间 $t$ 的确定性趋势函数。接下来，我们将介绍一些常用的趋势估计方法，这些方法能够帮助我们得出 $T_t$ 的估计值 $T^t$。理解这些方法的原理及各自的优缺点，对于进行准确的趋势估计至关重要。
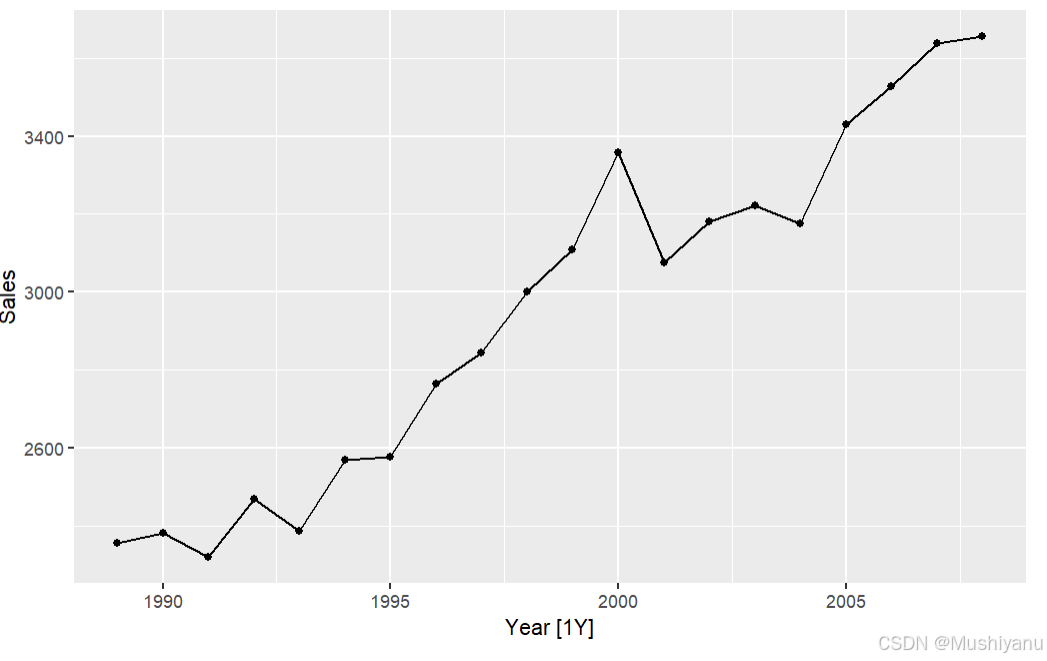
我们将通过以下示例来展示这些方法的应用和差异。

library(fpp3)
library(tsibble)
library(lubridate)
elecsales <-  read.table("C:/Users/LuoLi/Desktop/elecsales.txt")
head(elecsales)
T = dim(elecsales)[1]
da <- tsibble(Year=year("1989-01-01")+1:T-1,Sales=elecsales$V1,index=Year)
p1 <- autoplot(da,.vars = Sales) + geom_point();p1

趋势平滑方法

趋势平滑是估计时间序列中趋势成分的一种常用方法。它通过去除时间序列中的短期波动和随机噪声，使我们能够识别并分析长期趋势。常见的趋势平滑方法包括：

1. 参数回归法：通过假设趋势为已知形式的函数（如线性趋势或多项式趋势），并使用最小二乘法来估计回归系数，从而提取趋势成分。

2. 移动平均法：通过计算一定窗口内数据的平均值来平滑时间序列，这有助于去除短期波动并突出长期趋势。

3. 局部多项式回归法（LOESS）：利用局部加权回归方法，在每个数据点附近拟合一个多项式，从而平滑时间序列。这种方法适用于非线性趋势。

4. 指数平滑法：通过加权平均的方式，对时间序列数据进行平滑，其中较新的数据点会有更高的权重。指数平滑法常用于处理带有季节性和趋势的时间序列。

5. 核光滑法：通过核密度估计方法进行平滑，将每个数据点附近的其他点的加权平均作为该点的趋势值。这种方法能够处理非线性且没有固定形式的趋势。

趋势平滑方法之：参数回归法

1. 线性趋势模型
   最简单的假设是时间序列中的趋势成分服从一个已知形式的参数函数，例如线性趋势。线性趋势模型可以表示为：
   $$X_t=\alpha +\beta t+{ϵ}_t$$
   其中：

• $X_t$ 是时间点 $t$ 对应的观测值，
• $\alpha$ 和 $\beta$ 是待估计的参数，
• $t$ 是时间变量（通常是从 1 到 $n$），
• ${ϵ}_t$ 是随机误差项。
  为了估计参数 $\alpha$ 和 $\beta$，我们可以使用最小二乘法，最小化误差平方和：
  $$\underset{\alpha ,\beta }{\min }\sum _{t=1}^n(X_t-\alpha -\beta t{)}^2$$
  这里，目标是找到一条最佳的直线，使得预测值与实际观测值之间的误差最小。

2. 多项式趋势模型
   除了线性趋势之外，还可以假设时间序列中的趋势呈现更复杂的形式，例如多项式趋势。一个常见的多项式趋势模型为二次趋势，可以表示为：
   $$X_t=\alpha +\beta t+\gamma t^2+{ϵ}_t$$
   这里，$t^2$ 是时间的平方项，$\gamma$ 是待估计的参数。通过最小二乘法，我们同样可以估计参数 $\alpha$、$\beta$ 和 $\gamma$，目标是最小化误差平方和：
   $$\underset{\alpha ,\beta ,\gamma }{\min }\sum _{t=1}^n(X_t-\alpha -\beta t-\gamma t^2{)}^2$$

3. 非线性趋势模型
   除了线性和多项式趋势外，还可以假设更为复杂的非线性趋势。例如，Logistic 函数是一种常见的非线性趋势模型，它通常用于描述具有 S 形增长的时间序列数据。Logistic 函数模型可以表示为：
   $$X_t=\frac{a_1+b{e}^{-ct}}{1+e^{-ct}}+{ϵ}_t$$
   这里，$a_1$、$b$ 和 $c$ 是待估计的参数，$e$ 是自然对数的底数。该函数描述的是一个 S 形的曲线，可以用非线性最小二乘法来估计这些未知的参数：$$\underset{a,b,c}{\min }\sum _{t=1}^n(X_t-\frac{a_1+b{e}^{-ct}}{1+e^{-ct}}{)}^2$$

4. R 语言实现
   在 R 语言中，线性趋势可以通过 lm() 函数来拟合，而非线性趋势可以使用 nls() 函数来拟合。以下是一个用 R 来拟合线性趋势的示例代码：

# 线性趋势模型拟合
lmfit <- lm(Sales ~ Year, data=da)
b <- coef(lmfit)
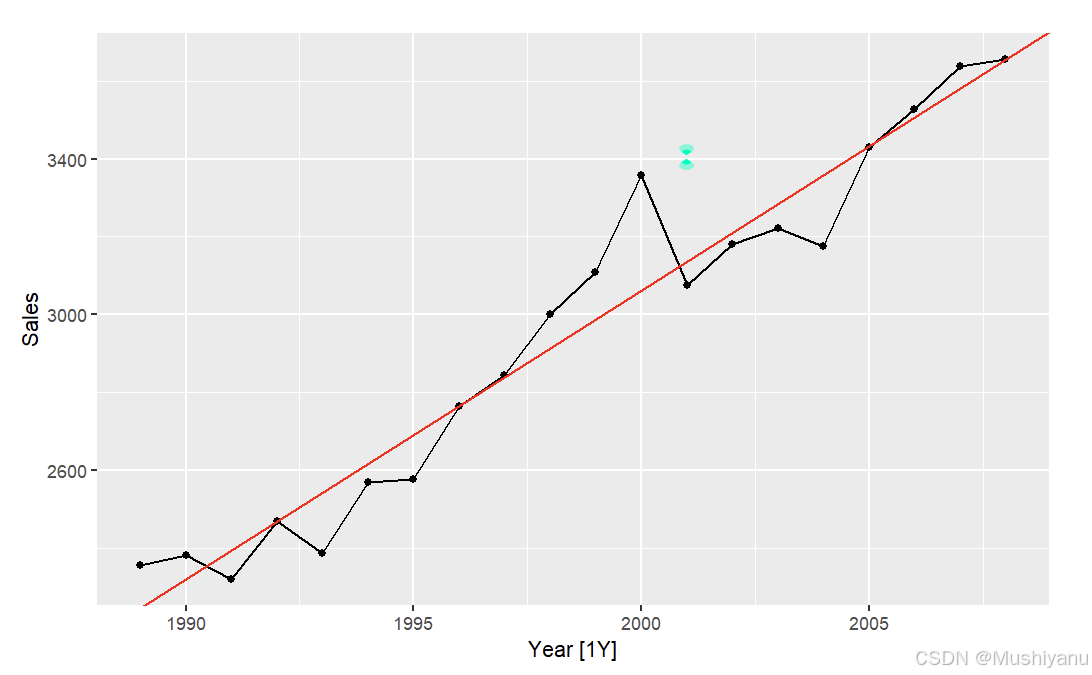
p1 + geom_abline(slope = b[2],intercept = b[1],col="red")

5. 总结

• 参数回归法的优点是：通过假设不同形式的趋势函数，并使用最小二乘法（线性回归、非线性回归等）来估计趋势成分。这种方法非常直观，适用于各种趋势形式的时间序列分析，帮助我们提取出时间序列的趋势信息。

• 参数回归法的缺点是：有限个参数所定义的全局函数常常不能很好的代表序列的多变趋势，因此实用性非常有限；

• 为此我们可以借鉴非参数回归的思想，不对趋势的具体形式做假设，而是采用局部平滑的方法来估计趋势。

趋势平滑方法之：移动平均法

移动平均法是一种常用的趋势平滑方法，它的基本思想是通过计算一段时间窗口内的数据平均值来估计某个时刻的趋势成分。

具体地，在某个时刻 $t$，我们希望估计该时刻的趋势值 $T_t$。移动平均法的步骤如下：

1. 选择一个时间窗口：我们考虑一个以时刻 $t$ 为中心的时间窗口 $[t-h,t+h]$，其中 $h$ 是窗口的半宽度，表示窗口的前后各包含 $h$ 个时刻的数据。

2. 计算窗口内的数据平均值：在这个时间窗口内，我们计算所有时刻的数据值的平均值，并用这个平均值作为时刻 $t$ 的趋势值估计。公式如下：
   $${\hat{T}}_t=\frac{1}{2h+1}\sum _{r=-h}^h{X}_{t+r}$$ 这里，$X_{t+r}$ 是时刻 $t+r$ 的观测值，$r$ 的取值范围是从 $-h$ 到 $h$，即在窗口 $[t-h,t+h]$ 内的所有时刻。

3. 随着时间推进，窗口右移：随着时间的推移，我们会不断移动时间窗口向右，即窗口的中心会逐渐右移，每次都会计算一个新的趋势值。通过这种方式，得到一系列的趋势估计。
   这种方法被称为 移动平均法（Moving Average），它通过平滑时间序列中的短期波动，帮助我们更好地识别长期趋势。

library(slider)
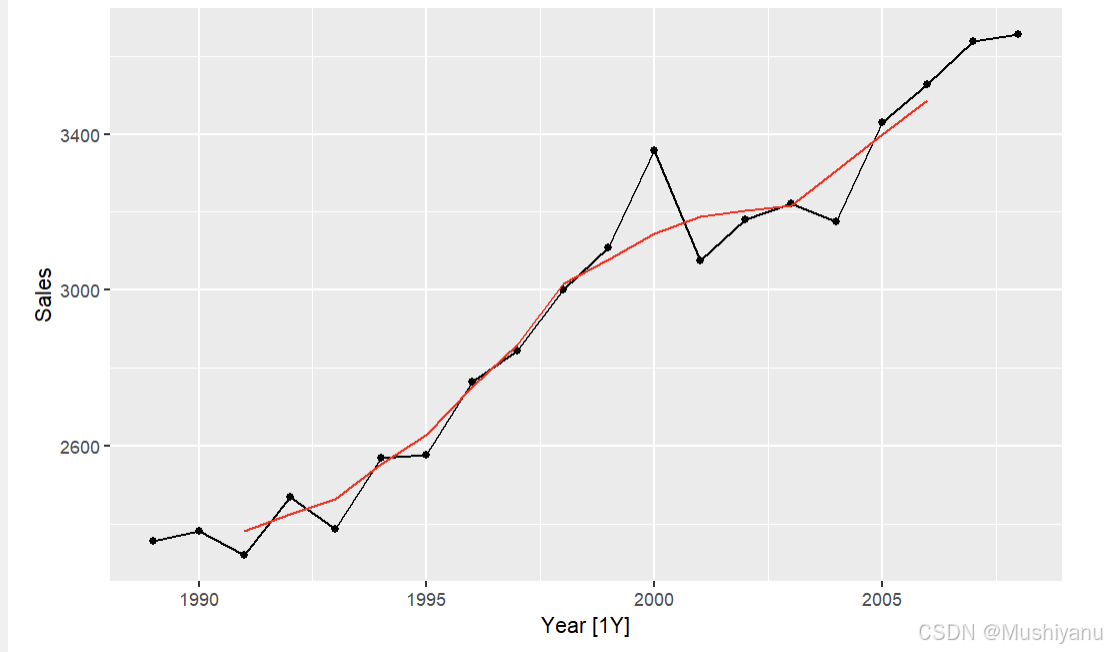
da <- mutate(da,`5-MA` = slide_dbl(Sales,mean,.before = 2,.after = 2,.complete = TRUE))
p1 + autolayer(da,.vars = `5-MA`,col="red")

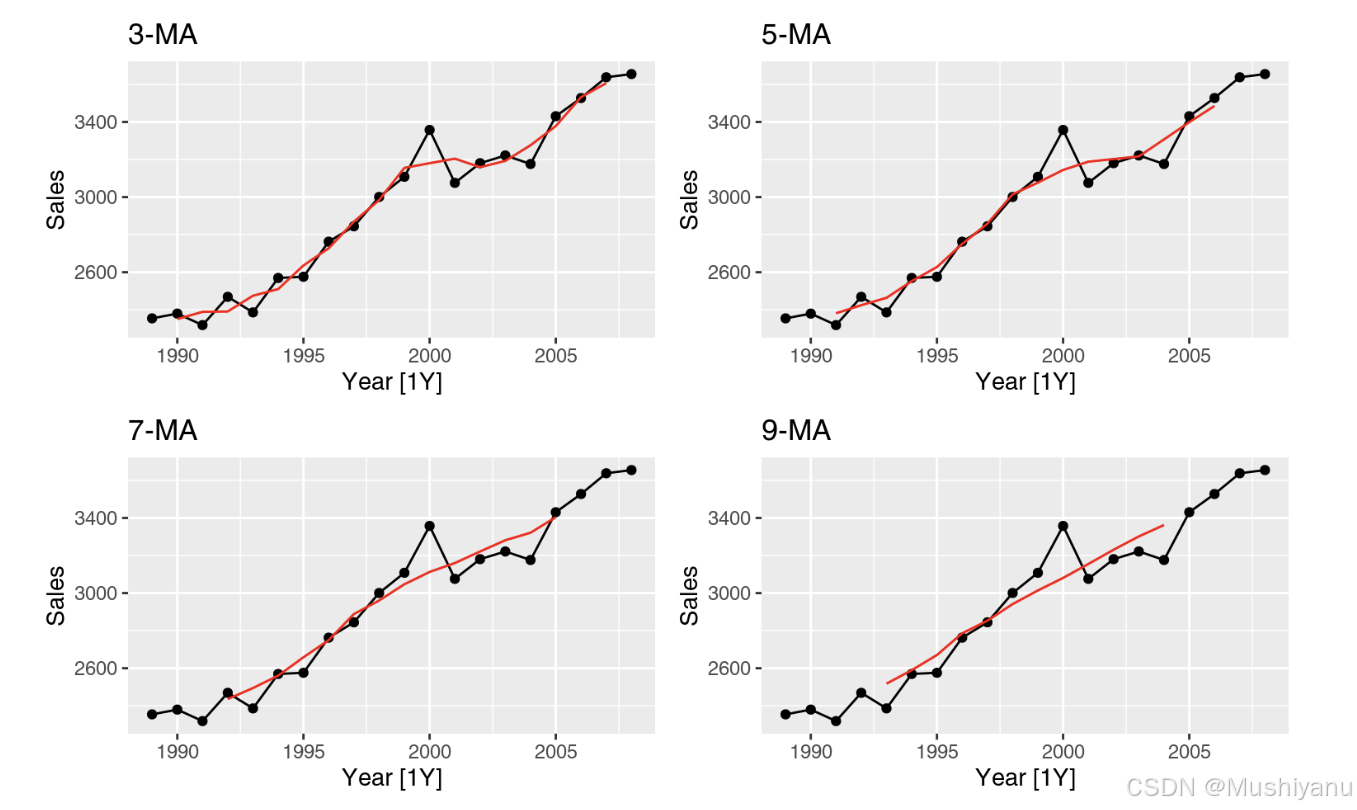
4. 移动平均法的窗宽控制了平滑程度
   在MA中，窗宽$2h+1$控制了平滑的程度，窗宽越大，则得到的趋势越平滑。下面的图比较了不同窗宽选择下的趋势平滑效果。
   
5. 总结
   移动平均法的优点在于其简单性和直观性，能够有效去除数据中的短期波动，突出长期的趋势变化。然而，缺点是它会在趋势变化较快的情况下产生滞后效应，导致趋势估计的反应速度较慢，并且无法得到两端各 $h$ 个点的趋势

趋势平滑方法之指数平滑法

指数平滑法是解决对称移动平均无法估计序列两端趋势问题的常用方法。它通过考虑非对称平滑来实现对时间序列的平滑处理，其中最著名的方法是简单指数平滑法。

1. 数学公式
   在指数平滑法中，我们对趋势的估计 $T^t$ 可以通过以下公式得到：$$\widehat{T_t}=\alpha X_t+\alpha (1-\alpha )X_{t-1}+\alpha (1-\alpha {)}^2{X}_{t-2}+\cdots$$
   这个公式可以扩展为无穷项的加权和：$$\widehat{T_t}=\sum _{j=0}^{\infty }\alpha (1-\alpha {)}^j{X}_{t-j}$$
   其中，$\alpha$ 是平滑常数，且满足 $0<\alpha <1$。我们注意到，随着 $j$ 增大，$X_{t-j}$ 的权重呈几何递减。$\alpha$ 控制了平滑的程度，即平滑值对于历史数据的敏感程度。

2. 预测公式
   指数平滑法还可以直接用于对未来的预测，其预测公式为：$${\hat{X}}_{T+1|T}=\alpha X_T+\alpha (1-\alpha )X_{T-1}+\alpha (1-\alpha {)}^2{X}_{T-2}+\cdots$$
   此外，还有一个递推公式可以描述指数平滑的预测过程：$${\hat{X}}_{T+1|T}=\alpha X_T+(1-\alpha ){\hat{X}}_{T|T-1}$$

3. 权重衰减
   从上述公式可以看出，指数平滑法生成的预测值是过去观测值的加权平均，而权重是随着过去观测值离预测值距离的增大而呈指数型衰减。这意味着，距离预测时间点较近的观察值权重较高，而距离较远的观察值权重较低。

4. 应用范围
   这种平滑方法被称为简单指数平滑法，它仅适用于没有明显趋势或季节性的时间序列。当时间序列中没有明显的趋势和季节性时，简单指数平滑可以有效地预测未来值。然而，由于它的局限性，简单指数平滑法的应用场景较为有限，但其原理可以扩展为更复杂的模型，如趋势平滑法和季节性指数平滑法等，并在实际中取得了广泛的应用。

• 关于指数平滑法更详细的介绍可以参看fpp3第8章。

趋势平滑方法之核光滑法

核光滑法是一种非参数的平滑技术，用于估计时间序列中的趋势。它通过给定数据的加权平均来计算平滑值，其中权重是根据数据点与当前时刻之间的距离来确定的。

1. 数学公式
   核光滑法的计算公式为：
   $$\widehat{T_t}=\sum _{i=1}^n{w}_{it}{X}_i$$
   其中，$w_{it}$ 是权重，计算方式为：
   $$w_{it}=\frac{K\left(\frac{i-t}{h}\right)}{{\sum }_{i=1}^{n}K\left(\frac{i-t}{h}\right)}$$

• $K(\cdot )$ 是核函数，通常取标准正态分布的密度函数，即：

$$K\left(\frac{i-t}{h}\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(i-t{)}^2}{2h^2}}$$

• $h$ 是窗宽，控制权重衰减的程度。窗宽越小，距离 $t$ 较远的数据点的权重衰减越快。

2. 方法思想
   核光滑法的核心思想是：给定时刻 $t$，对 $t$ 附近的数据点给予较大的权重，而对远离 $t$ 的数据点赋予较小的权重。这样，通过对历史数据的加权平均，可以去除序列中的噪音并平滑出趋势成分。

3. 应用范围
   核光滑法主要用于估计时间序列的趋势成分。它无法用于预测未来的值，因为它只依据现有数据来平滑历史数据。因此，核光滑法的目标是帮助我们观察数据的长期趋势，而非进行未来的预测。

4. R实现

在R中，ksmooth 函数可以用来执行核光滑操作。该函数实现了上述计算公式，可以应用不同的核函数来平滑数据，并输出趋势的估计值。

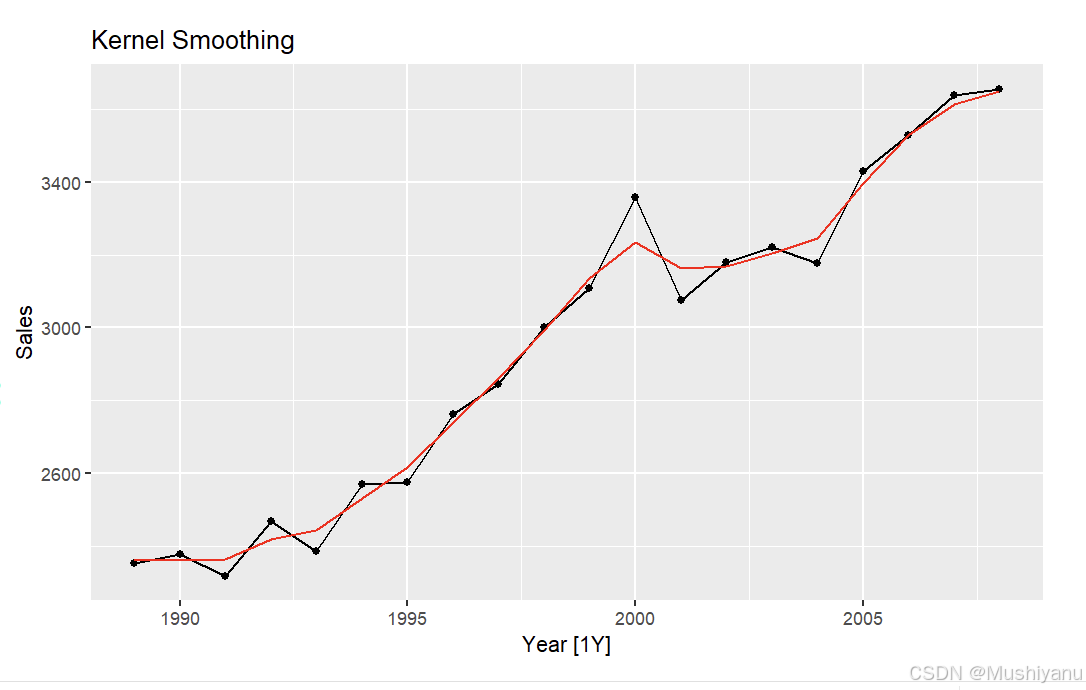
ks.fit <- ksmooth(da$Year,da$Sales,kernel = "normal", bandwidth=2,x.points = da$Year)
da <- mutate(da,KS = ks.fit$y)
p1 + autolayer(da,.vars = KS,col="red")+labs(title="Kernel Smoothing") 

趋势平滑方法之局部多项式回归法（LOESS）

局部多项式回归（LOESS，Locally Estimated Scatterplot Smoothing）是一种通过局部拟合多项式来平滑数据的非参数回归方法。其核心思想是，在每个数据点 $t$ 附近选择一些最接近的点，利用这些点通过加权最小二乘法拟合一个多项式，并将多项式在点 $t$ 处的值作为该点的趋势估计。

1.选择邻近点

• 目标: 在时间序列的某个点 $t$ 处估计其趋势值。
• 选择邻近点: 我们选择距离点 $t$ 最近的 $75\%$ 的数据点（这个比例是默认值，也可以调整）。这些点用于局部拟合。

2.加权最小二乘法

• 加权最小二乘法: 对选定的邻近点使用加权最小二乘法进行拟合。在加权最小二乘法中，每个点的权重根据其与点 $t$ 的距离来确定，距离越远的点权重越小。具体地，点 $i$ 距离点 $t$ 越远，权重 $w_i$ 就越小，权重函数通常是一个衰减函数（例如，高斯函数）。

3.拟合多项式

• 拟合多项式: 使用加权最小二乘法对选定的邻近点拟合一个多项式。默认情况下，通常选择二阶多项式（即二次多项式）。这个多项式能够捕捉局部的数据趋势。
• 拟合出的多项式: 拟合出的多项式的在点 $t$ 处的值，便被认为是该时刻的趋势值。

4.点 $t$ 处的趋势值

• 趋势值: 拟合后的多项式在点 $t$ 处的值即为该点的趋势估计。由于每个时刻的拟合多项式不同，因此趋势值会随着时间变化而变化。

5.公式表示
假设我们选择点 $t$ 附近的一组数据点 $X_i$，其对应的目标变量为 $Y_i$，加权最小二乘法的目标是最小化：
$$\underset{{\beta }_0,{\beta }_1,{\beta }_2}{\min }\sum _i{w}_i(Y_i-{\beta }_0-{\beta }_1{X}_i-{\beta }_2{X}_i^2{)}^2$$
其中，$w_i$ 是点 $i$ 到点 $t$ 的距离的加权系数，距离越远，$w_i$ 越小。

6.总结

• LOESS 通过局部拟合多项式来平滑时间序列数据，解决了全局平滑方法可能失去局部趋势变化的问题。
• 该方法灵活且能够适应数据的局部波动，是一种有效的非参数回归方法。
• 由于每个点的趋势值都是基于周围点局部拟合得到的，因此，当 $t$ 变化时，拟合的多项式也会不同，能够更准确地捕捉到数据中的局部变化。

7. R实现

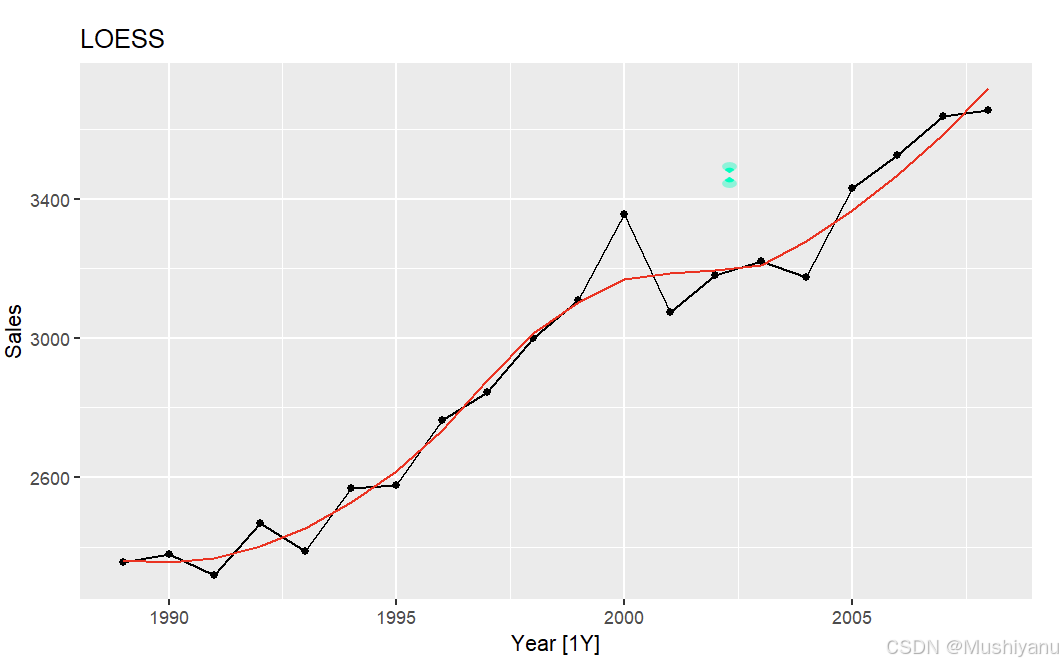
loess.fit <- loess(Sales ~ Year, data=da, span=0.6)
da <- mutate(da,LOESS = loess.fit$fitted)
#da
p1 + autolayer(da,.vars = LOESS,col="red")+labs(title="LOESS")

对一个同时包含趋势性和季节性的时间序列进行趋势平滑

1.获得趋势性

• 先看一个例子

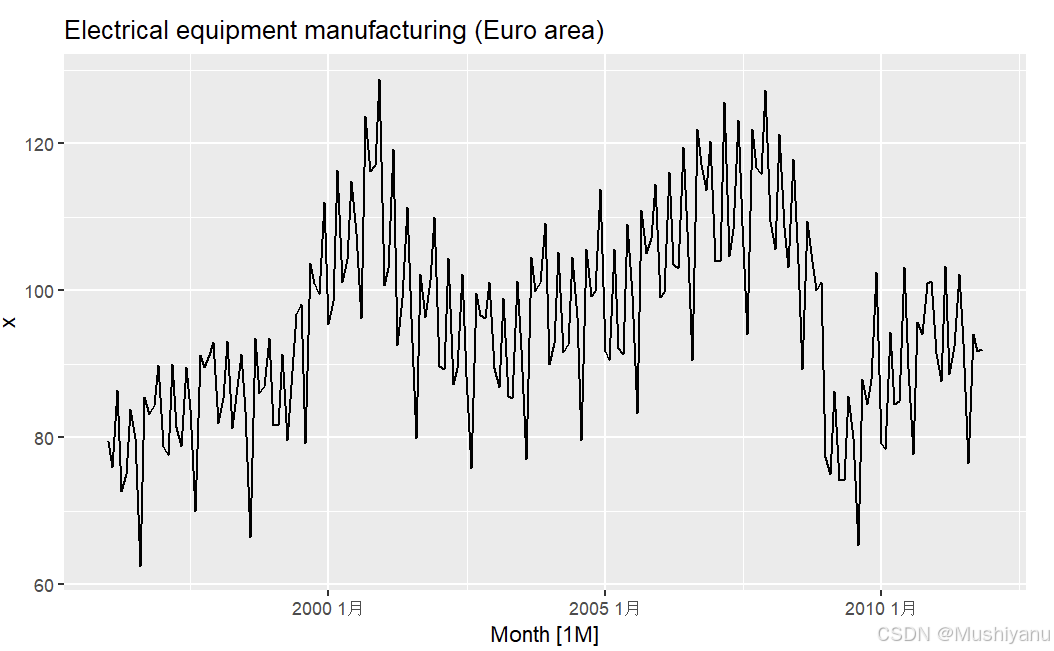
elecequip <-  read.csv("C:/Users/LuoLi/Desktop/elecequip.csv",header = TRUE);T = dim(elecequip)[1]
da2 <- tsibble(Month = yearmonth("1996-01-01")+1:T-1, 
               x=elecequip$x,
               index=Month)
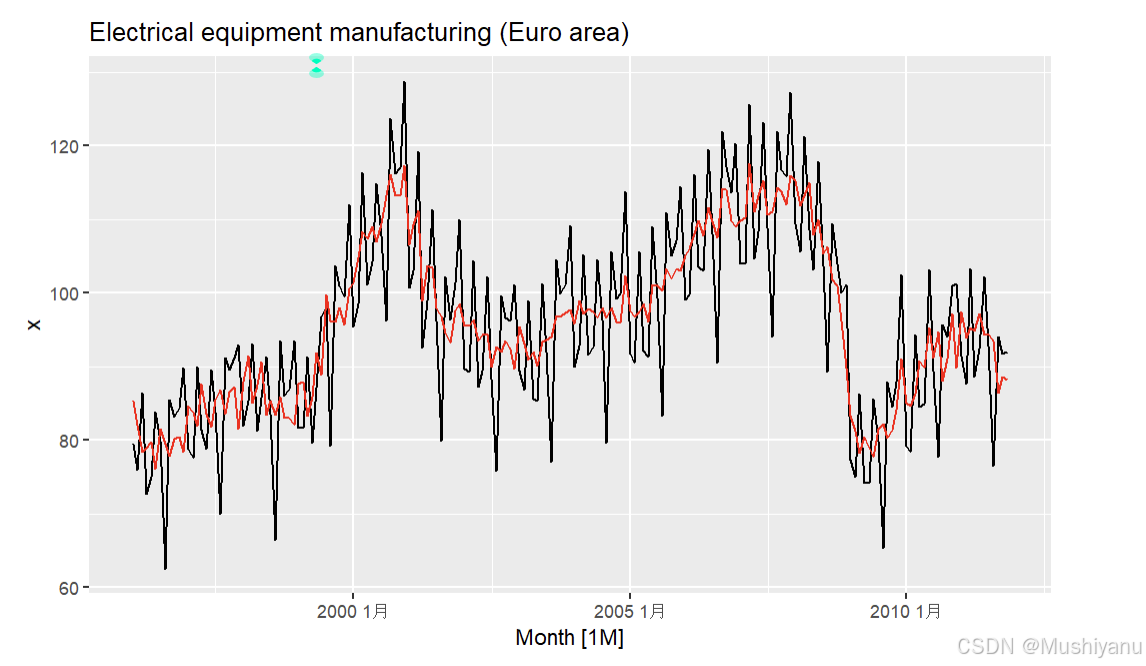
p1 <- autoplot(da2,.vars=x) + ggtitle("Electrical equipment manufacturing (Euro area)");p1

• 当我们对季节性时间序列进行趋势平滑时，我们必须选择季节长度作为窗宽才能消除掉季节性的影响；然而常见的季节性序列如季度数据和月度数据，周期长度都是偶数；无法进行对称的移动平均；这时通常采用的方法是：先做一次窗宽为周期的非对称MA平滑，然后对平滑后的序列再做一次窗宽为2的移动平均。
• 以季度数据为例，对4-MA后的序列再进行一次2-MA，则有
  $${\hat{T}}^t=\frac{1}{2}\left[\frac{1}{4}(y_{t-2}+y_{t-1}+y_t+y_{t+1})+\frac{1}{4}(y_{t-1}+y_t+y_{t+1}+y_{t+2})\right]$$
  即
  $${\hat{T}}^t=\frac{1}{8}{y}_{t-2}+\frac{1}{4}{y}_{t-1}+\frac{1}{4}{y}_t+\frac{1}{4}{y}_{t+1}+\frac{1}{8}{y}_{t+2}$$
  一般情况下， $2\times m-MA$ 等同于 $m+1$ 阶移动平均，但是两端的权重为 $\frac{1}{2m}$，其余处的权重为 $\frac{1}{m}$。

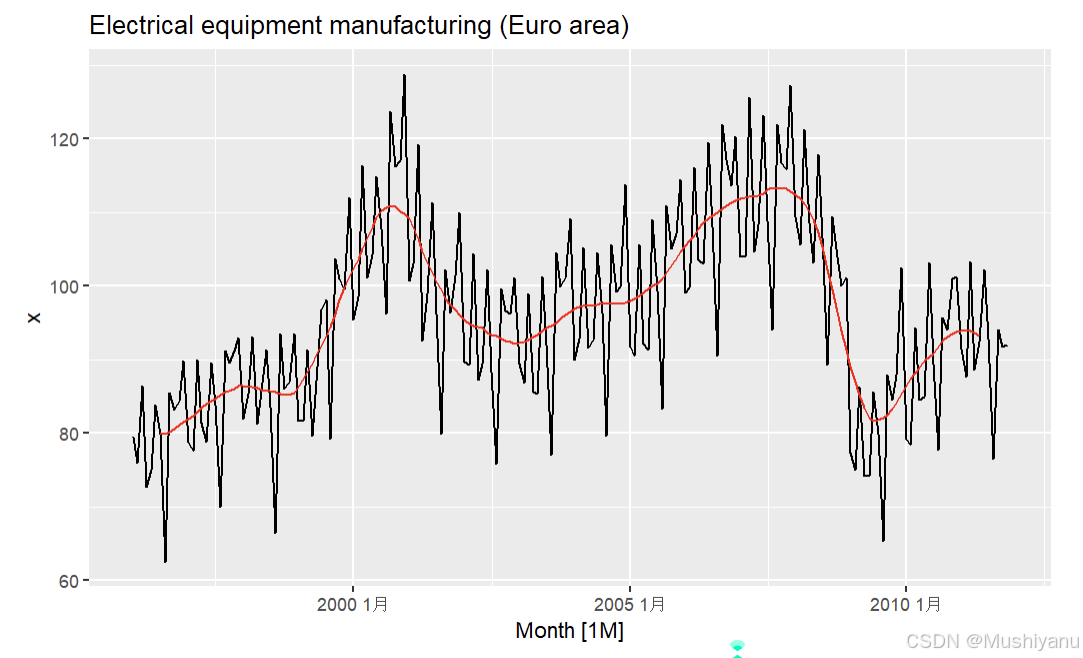
da2 <- mutate(da2,
              `12-MA`=slide_dbl(x,mean,.before = 5,.after = 6,.complete = TRUE),
              `2*12-MA`=slide_dbl(`12-MA`,mean,.before = 1,.after = 0,.complete = TRUE))
p1 + autolayer(da2,.vars = `2*12-MA`,linewidth=0.7,col="red")

季节指数的构造

• 利用趋势平滑得到趋势成分之后，就可以从原序列中消除趋势性，现在对去除趋势之后的季节性时间序列构造季节性成分。

2.消除趋势性

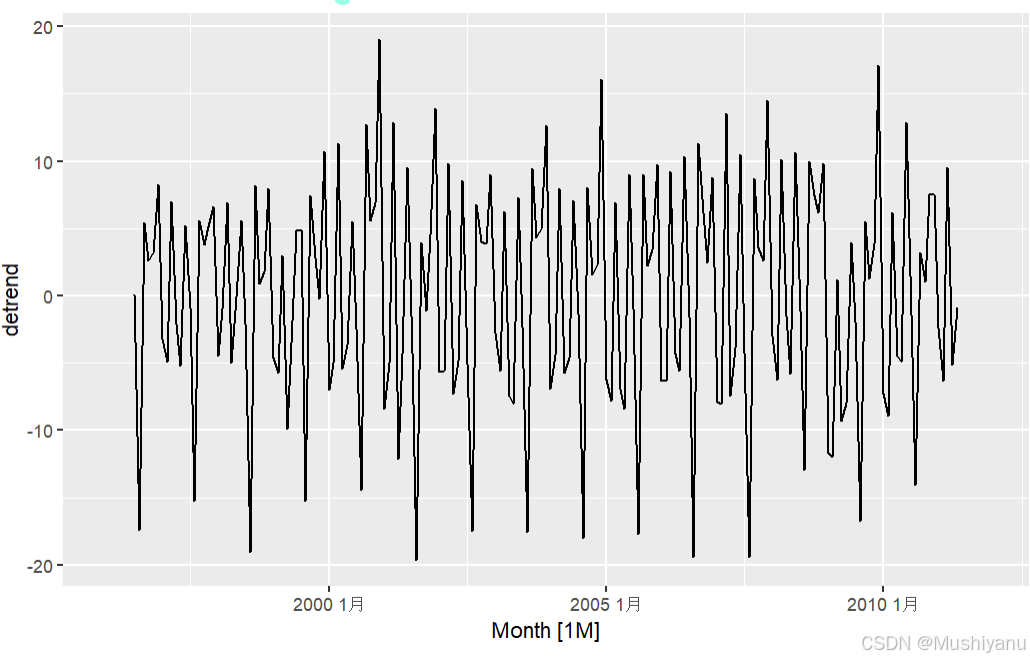
da2 <- mutate(da2,detrend=x-`2*12-MA`)
p2 <- autoplot(da2,.vars = detrend);p2

3.构造季节指数

在加法模型中，季节性成分 $S_t$ 的假设包括以下两点：

1. 季节性几乎不变：假设 $S_t\approx S_{t-12}$，即季节性成分每年保持相似。这表示季节性成分在相隔 12 个月的时间点上是近似相同的。

2. 模型可识别性条件：要求一年的周期内季节性成分的总和为零：
   $$\sum _{t=1}^{12}{S}_t=0$$
   这个条件确保模型的可识别性，即排除不同因素的相互影响，使得季节性成分在模型中清晰独立。

构造季节指数的步骤如下：

• 为了估计 $S_1$，我们可以计算所有 1 月份数据的均值 ${\hat{S}}_1$；同理，$S_2$ 则计算 2 月份数据的均值 ${\hat{S}}_2$，以此类推。

• 为满足总和为零的条件，对所有的季节性成分 $\widehat{S_1},\widehat{S_2},\dots ,\widehat{S_{12}}$ 进行中心化处理。

中心化处理公式

定义季节性成分的均值 $\bar{S}$ 为：$$\bar{S}=\frac{1}{12}\sum _{t=1}^{12}{\hat{S}}_t$$

然后对每个季节性成分 $S_t$ 进行调整，以确保总和为零：$${\hat{S}}_t\leftarrow {\hat{S}}_t-\bar{S}$$

通过这种中心化方法，季节性成分的总和可以满足上述可识别性条件。

• 这个过程的R代码如下

month.mean = c()
for(i in 1:12)
{
  month.mean[i] = da2$detrend[month(da2$Month)==i] |> na.omit() |> mean()
}
season <- month.mean-mean(month.mean)
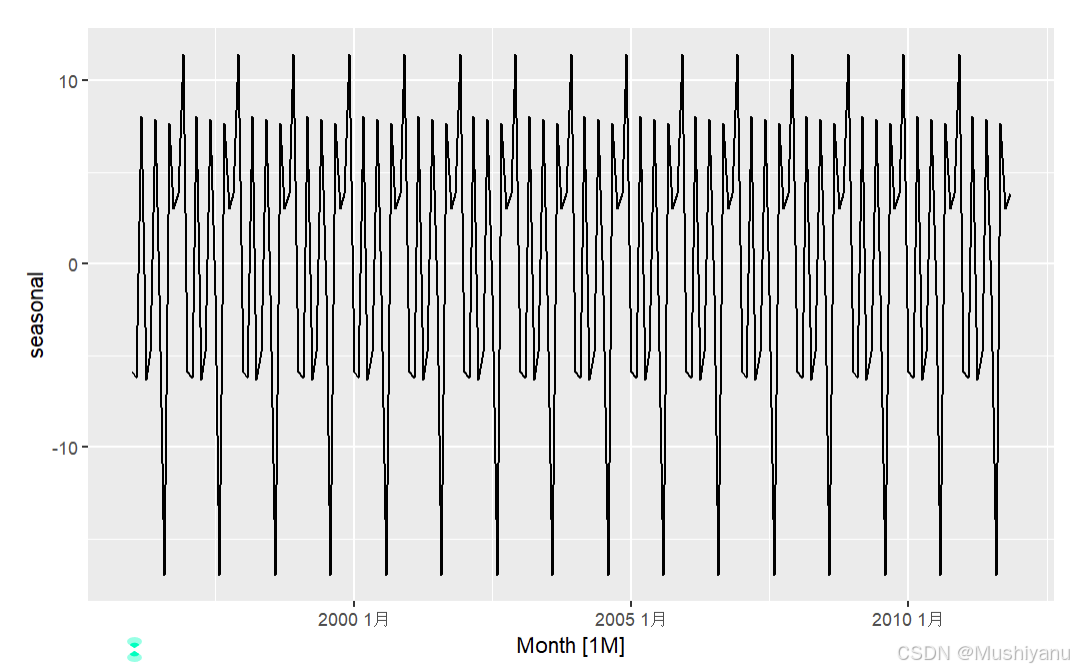
da2 <- mutate(da2, season = rep_len(season,T))
autoplot(da2,.vars=season)+ylab("seasonal")

4.消除季节性（季节调整）

• 从序列中消除季节性，从而更好地显示序列趋势，这一过程在经济里称为季节调整，是一种非常重要的数据处理手段。国家宏观调控部门发布的很多数据都要先做季节调整。对于加法模型而言，季节调整即求
  $$x_t-\widehat{S^t}$$

da2 <- mutate(da2,x.adj=x - season)
p1 + autolayer(da2,.vars = x.adj,linewidth=0.7,col="red") 

经典分解法

经典分解法（Classical Decomposition）是一种将时间序列数据分解为趋势成分、季节性成分和随机成分的常用方法。

基于加法模型的经典分解原理：

1. 用移动平均得到趋势性 $\widehat{T_t}$；
2. 利用 $X_t-\widehat{T_t}$ 得到季节指数 $\widehat{S_t}$；
3. 利用 $\widehat{{ϵ}_t}=X_t-\widehat{T_t}-\widehat{S_t}$ 得到剩余成分。

基于乘法模型的经典分解原理：

1. 用移动平均得到趋势性 $\widehat{T_t}$；
2. 利用 $\frac{X_t}{\widehat{T_t}}$ 构造季节指数，注意此时季节指数要归一化而不是中心化，即 $\widehat{S_t}\leftarrow \frac{\widehat{S_t}}{\bar{S}}$；
3. 利用 $\widehat{{ϵ}_t}=\frac{X_t}{\widehat{T^t}\cdot \widehat{S^t}}$ 得到剩余成分。

R中的经典分解法

• 上面我们介绍的是经典分解法的原理；在R里，可以直接用函数decompose来进行经典分解；

• 下面是feasts::classical_decomposition的用法，components()可以输出趋势项，季节项，随机项等分解结果；

cd <- model(da2,classical_decomposition(x))
cd.out <- components(cd); cd.out[10:12,]

结果解释：

1. .model：这列显示的是使用的分解模型，这里显示的是 classical_decomposition(x)，表明你正在使用经典分解方法对时间序列数据 x 进行分解。

2. Month：显示的是时间戳信息，具体是时间序列的月份。这里分别是1996年的10月、11月和12月。

3. x：原始的时间序列数据（即观测值），显示的是每个月的实际数据。例如，1996年10月的观测值是83.19。

4. trend：趋势成分，这是通过平滑方法（如移动平均）计算得出的，表示时间序列数据中的长期趋势。例如，1996年10月的趋势成分为80.59083，表示该月的长期趋势值。

5. seasonal：季节性成分，表示时间序列的季节性波动。它显示了某个月份的季节性影响，通常与趋势成分比较。例如，1996年10月的季节性成分为3.030387，表示该月的季节性波动高于趋势值。

6. random：残差成分，表示时间序列数据中的噪声或无法用趋势和季节性解释的部分。例如，1996年10月的残差成分为-0.4312204，表示该月的数据偏离趋势和季节性模式的部分。

7. season_adjust：季节调整后的数据，是从原始数据中去除季节性成分后的结果，旨在剔除季节性波动，以便分析其他因素对数据的影响。例如，1996年10月的季节调整数据为80.15961，表示去除季节性波动后的数据。

1996年10月：

• 原始数据为83.19。
• 趋势成分为80.59083，表示长期趋势的水平。
• 季节性成分为3.030387，表示10月的季节性波动。
• 残差为-0.4312204，表示随机噪声。
• 季节调整后的数据为80.15961，表示去除季节性波动后的结果。

通过这些成分的分解，可以更清晰地看到每个时间点的原始数据是如何受到长期趋势、季节性变化和随机噪声的影响。季节调整后的数据可以用来进行更准确的趋势分析，排除季节性因素的干扰。

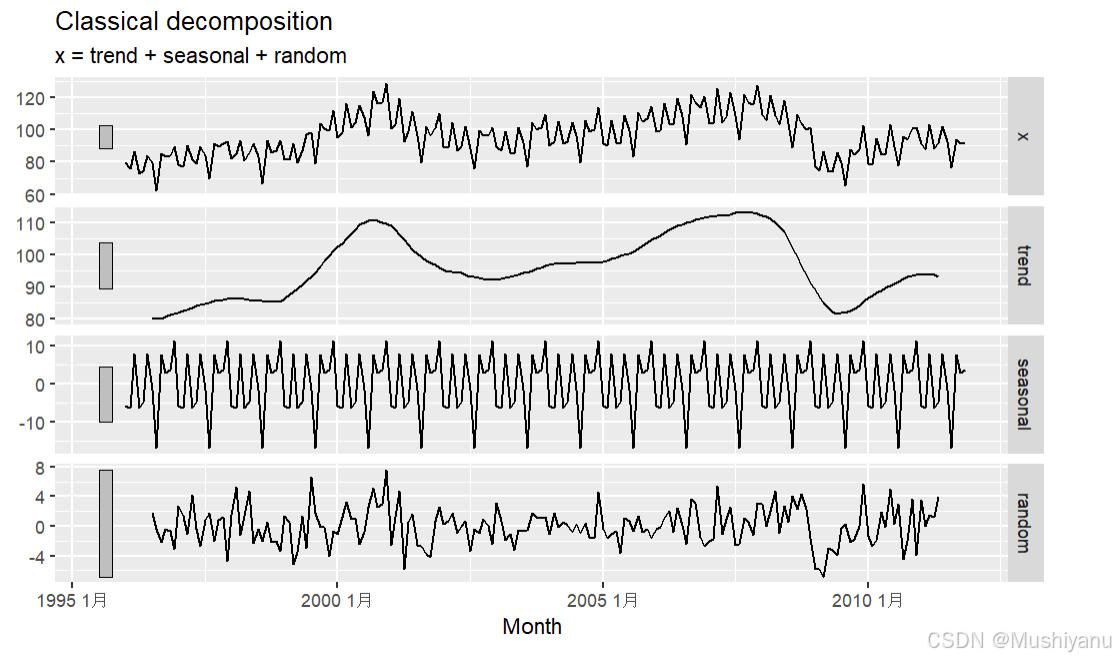
autoplot(cd.out)

经典分解法的评价

经典分解法的缺点主要包括以下几点：

1. 无法对两端的趋势进行估计：
   经典分解法使用移动平均来估计趋势成分，但移动平均的计算方式导致它不能有效估计时间序列两端的趋势成分。此外，由于无法估计两端的趋势，经典方法也不能得到这两端的非规则项（随机成分）。

2. 季节因子假设恒定不变：
   经典分解法假设季节性因素（季节因子）是恒定不变的。然而，这一假设在实际应用中并不总是成立。例如，随着技术进步（如空调的普及），一些产品或服务的季节性需求特征可能会发生变化，从而使得季节因子不再恒定。因此，这种假设可能在长期时间序列中变得不太合理。

3. 对异常观测值不稳健：
   经典分解法在面对异常观测值时缺乏鲁棒性。即使数据中出现一些离群值或极端情况，这种方法也可能给出不可靠的结果，影响整体的分解精度。

4. 综合评价
   由于上述原因，经典分解法在实际应用中并不总是理想的选择，尤其是在存在更好的替代方法时。尽管经典分解法仍然可以在某些简单的场景中使用，但如果我们有更先进的季节调整和趋势分解方法（如X-11、SEATS等），建议优先选择这些方法，以获得更准确和稳健的分析结果。

介绍：官方统计机构使用的季节调整和分解方法：X-11过程

在经济统计中，季节调整是一项至关重要的工作，它能帮助消除季节性波动对数据分析的影响。X-11过程是一种广泛使用的季节调整方法，它自20世纪50至60年代由美国调查局和加拿大统计局开发以来，已经被多个国家的官方统计机构采纳，并且经历了多个版本的演变。现在，X-11过程已经发展成为X-13ARIMA-SEATS（简称X11）方法，并成为全球范围内官方统计机构的标准工具。

X-11过程的基本原理

X-11过程基于经典分解法，其基本思想是将时间序列分解为趋势、季节性和随机成分。然而，X-11在经典分解法的基础上做了多项改进，以解决经典方法的缺点：

1. 得到两端的趋势估计：经典分解法无法有效估计时间序列两端的趋势成分，而X-11能够克服这一问题，提供更精确的趋势估计。

2. 季节项随时间变化：X-11允许季节性成分随时间缓慢变化，以适应经济数据中季节性波动的动态特性。

3. 处理日历效应：X-11特别强调在季节性估计中考虑日历效应，例如交易日效应、假日效应以及其他预测变量对季节性影响的作用。例如，中国农历春节每年日期不同，可能出现在一月或二月，这种变化会显著影响消费和生产等经济数据。

4. 考虑特殊日历效应：X-11也能处理如假日等特殊日历因素的影响，确保季节性调整的准确性。

X-11与X-13ARIMA-SEATS

X-13ARIMA-SEATS是X-11的升级版，它集成了更先进的时间序列分析方法，例如ARIMA模型（自回归积分滑动平均模型）。X-13ARIMA-SEATS可以同时进行加法和乘法模型的季节调整分解。

在R中的实现

在R中，用户可以通过seasonal包实现X-11和X-13ARIMA-SEATS方法。这个包提供了X-11和SEATS两种算法的实现，其中：

• SEATS（Seasonal Extraction in ARIMA Time Series）最早由西班牙银行开发，现在被全球的政府和统计机构广泛采用。

这些方法专门用于分析季度数据和月度数据，不适用于年度数据。

• 我们还是以前面的数据为例

library("seasonal")
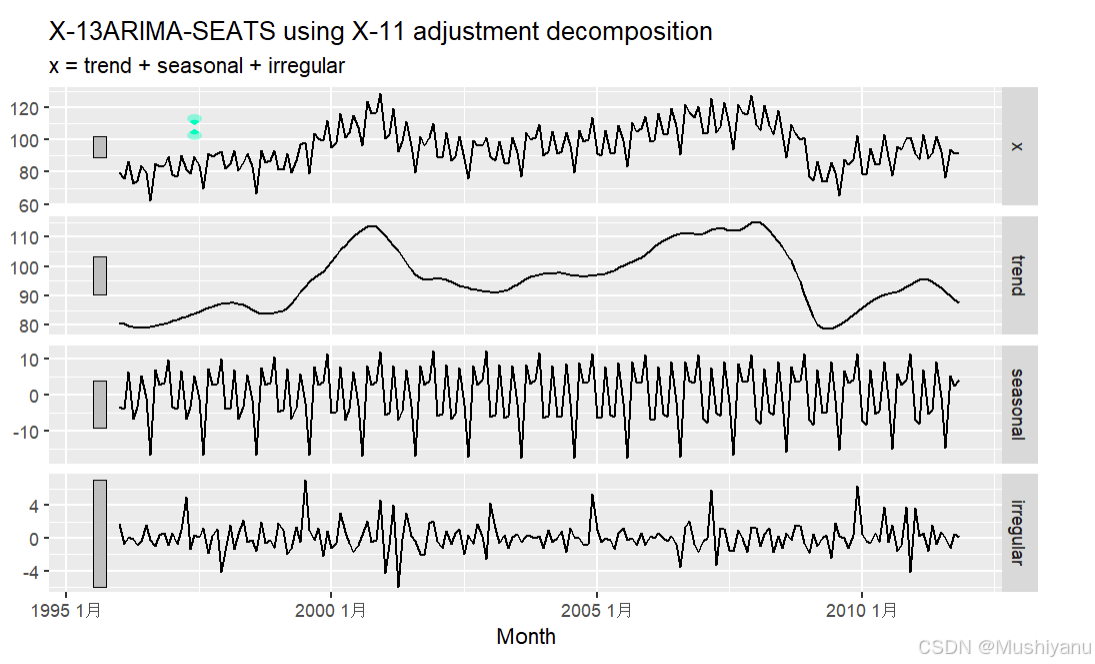
X11 <- model(da2,X_13ARIMA_SEATS(x~x11()+transform(`function`="none")))
X11.out <- components(X11)
autoplot(X11.out)

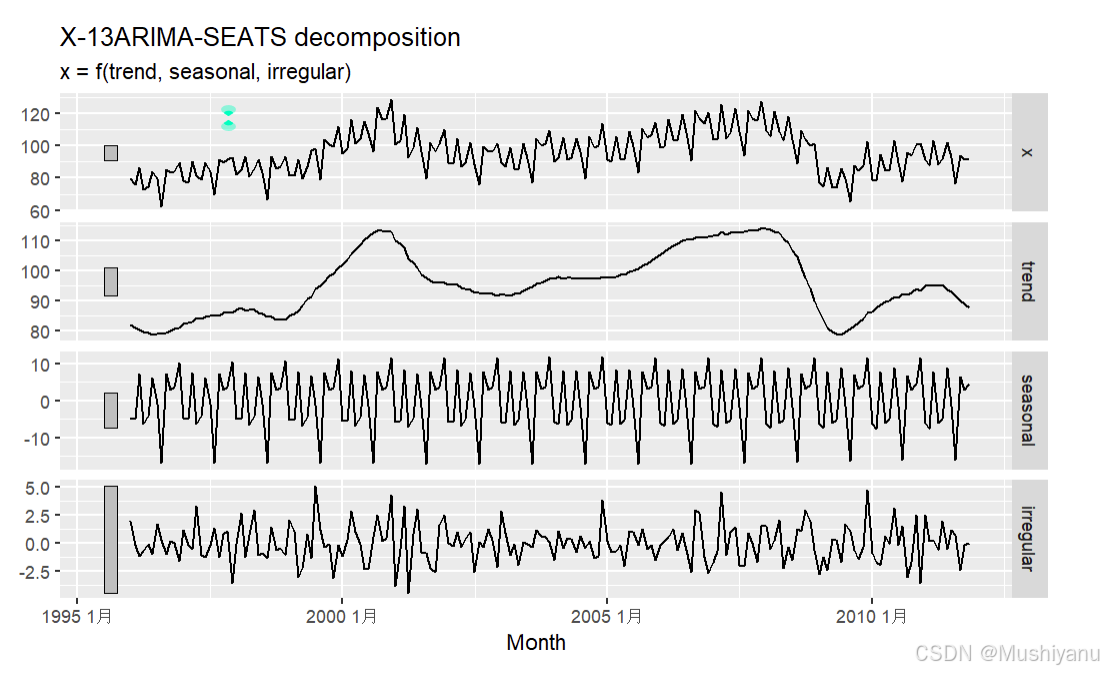
SEATS <- model(da2,X_13ARIMA_SEATS(x~seats()+transform(`function`="none")))
SEATS.out <- components(SEATS)
autoplot(SEATS.out)

• 这里X_13ARIMA_SEATS()是通过调用seasonal包中的相应函数来分别实现X11过程分解和SEATS分解；两者的分解结果通常比较接近。

• 关于X-13ARIMA-SEATS方法的详细原理介绍超出本笔记学习的范围，感兴趣的同学可以研究seasonal包的帮助文档以及里面引用的专著和文献.

• 关于seasonal包的详细介绍，可以参看Introduction to Seasonal 或者文档Seasonal Adjustment by X-13ARIMA-SEATS in R

• X-13ARIMA-SEATS广泛使用了ARIMA模型和ARMAX模型来处理异常点，假日效应和其它预测变量效应，因此我们将在学习完相关内容之后再回过头来理解该程序的处理原理。

STL分解法

STL（Seasonal and Trend Decomposition using LOESS）是一种基于局部加权回归的时间序列分解方法，其中LOESS（局部加权回归平滑）是一种非参数的趋势平滑方法。

STL分解法由R. B. Cleveland, W. S. Cleveland, McRae 和 Terpenning于1990年提出。STL分解法具有以下优点和缺点：

优点：

1. 处理任意形式的季节性：
   STL分解法不像X11和SEATS方法那样仅限于季度数据和月度数据，它能够处理具有不同季节性模式的时间序列。因此，STL可以广泛应用于各种类型的时间序列数据，而不受时间频率的限制。

2. 季节成分随时间变化：
   STL分解法允许季节成分随着时间变化。这意味着它能够灵活地适应时间序列中季节模式的变化。季节成分的变化速率由用户控制，因此可以根据需要调整变化的速度。

3. 趋势成分的光滑程度可控：
   STL分解法中的趋势成分可以进行光滑，光滑的程度同样由用户控制。用户可以根据实际需求控制趋势的平滑程度，从而获得更加准确的趋势估计。

4. 对异常点稳健：
   STL分解法具有较强的鲁棒性，对于偶尔出现的异常点不会影响整体的趋势-周期项和季节项的分解。这使得STL适用于一些存在异常值的时间序列数据。

缺点：

1. 仅支持加法模型：
   STL分解法只能处理加法模型（Additive Model）。虽然可以通过取对数将加法模型转化为乘法模型，但STL本身不直接支持乘法模型分解。

2. 无法自动处理日历效应和交易日效应：
   STL分解法不自动处理日历效应（如节假日的影响）和交易日效应（如工作日与非工作日的差异）。然而，X11和SEATS等方法能够处理这些效应。在STL分解之前，可以通过对数据进行适当的预处理（如去除日历效应）来补充这一缺陷。

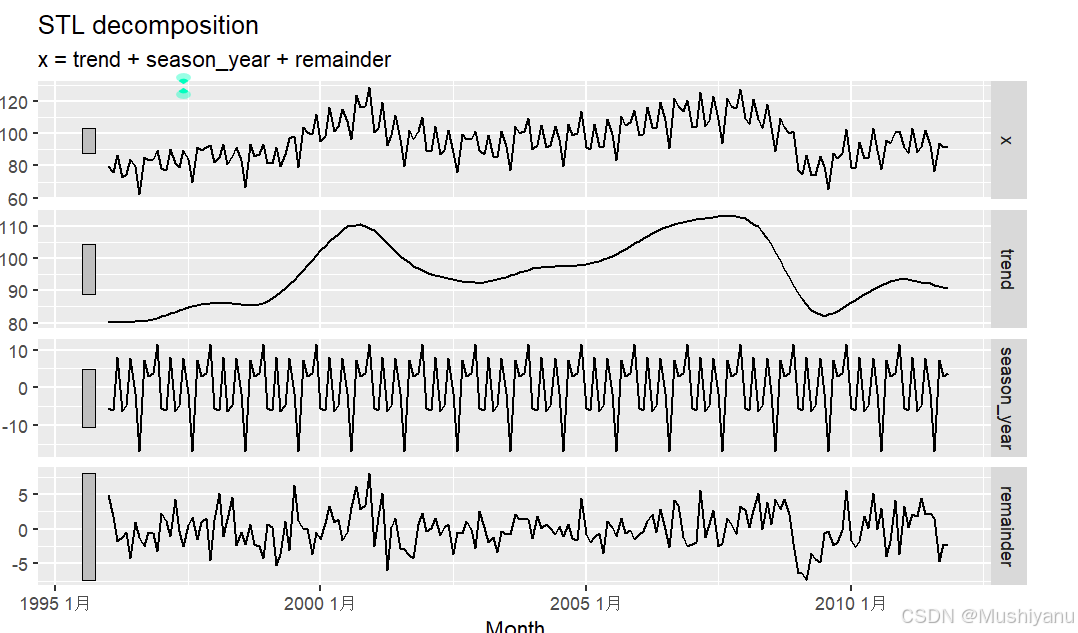
STL <- model(da2,STL(x ~ trend(window=21)+
                                season(window="period")))
STL.out <- components(STL)
autoplot(STL.out)

在使用 STL 进行时间序列分解时，有两个关键参数需要选择：趋势窗宽和季节窗宽。

1. 趋势窗宽 (trend(window = ?)):

   • 定义：趋势窗宽控制了趋势成分的变化速度。它决定了在每个时点如何估计趋势值。较小的趋势窗宽意味着趋势成分会更加灵活，变化更快；而较大的趋势窗宽会导致趋势估计更加平滑，变化较慢。
   • 设置：窗口的大小应该是一个奇数，这样可以保证对称性。通常，窗口越小，趋势变化的速度越快。

2. 季节窗宽 (season(window = ?)):

   • 定义：季节窗宽控制了季节成分的变化速度，决定了用于估计季节性成分时考虑的前后观测数据的数量。它对每个季节值的估计依赖于一定数量的相邻年份数据。较小的季节窗宽允许季节成分快速变化，而较大的季节窗宽则使季节成分更加平稳。
   • 设置：季节窗宽也需要是一个奇数。设置较小的值允许季节性变化更加快速和灵活；而将季节窗宽设置为无穷大或使用periodic选项，相当于假设季节成分是时间不变的。

影响：

• 趋势窗宽和季节窗宽的选择直接影响到STL分解后的趋势成分和季节成分的平滑程度及灵活性。
• 较小的窗口值使得模型可以捕捉到更快的变化，而较大的窗口值则使得模型对较长周期的变化更敏感。

总结：

• 趋势窗宽控制了趋势的变化速度，较小的值会使趋势变化更加灵活。
• 季节窗宽控制了季节变化的速度，较小的值使季节变化更加快速，设置为periodic或无穷大时，假设季节成分是固定不变的。

补充：

tsibble 对象

tsibble 对象是 R 中 tsibble 包的一种专门用于处理时间序列数据的数据结构，它继承自 数据框（data frame），但通过扩展和增强提供了更强大的时间序列处理能力。tsibble 的设计使得它特别适用于处理不规则的时间序列数据，并且与 tidyverse 包（如 dplyr、ggplot2）兼容，可以进行灵活的数据操作和可视化。

tsibble 对象的特点

1. 时间索引（Time Index）：

   • tsibble 包含一个或多个时间索引（index），通常是一个表示时间的列（例如日期、年份等），用于标识时间序列的时间顺序。

2. 键（Key）：

   • 可以为 tsibble 对象指定一个或多个键（key），这对于处理包含多个时间序列的数据特别重要。例如，如果数据中包含多个产品、区域或类别的时间序列，可以使用键来区分不同的时间序列。

3. 支持不规则数据：

   • tsibble 支持不规则的时间序列数据，这意味着可以处理缺失的时间点或间隔不一致的时间序列数据。

4. 与 tidyverse 兼容：

   • tsibble 对象与 tidyverse 包（如 dplyr 和 ggplot2）兼容，用户可以使用标准的 tidyverse 函数来操作和可视化时间序列数据。

5. 自动处理缺失值：

   • tsibble 可以自动识别时间序列中的缺失值并进行适当的处理，方便后续分析。

6. 增强的时间序列建模功能：

   • tsibble 包与 fable（一个时间序列建模包）紧密结合，能够进行建模、预测和评估。

tsibble 对象的创建

可以通过 tsibble() 函数将数据框或其他对象转换为 tsibble 对象。tsibble() 需要指定 时间索引（index） 和可选的 键（key）。

创建 tsibble 对象的基本语法：

tsibble(data, ..., index = NULL, key = NULL)

• data：输入的数据框（data frame）。
• …：其他数据列，通常是时间序列的各个变量。
• index：指定时间列，通常是表示时间的列（如年份、日期等）。
• key：指定一组键，用于区分多组时间序列数据（例如不同的产品、地区等）。

示例

1. 创建基本的 tsibble 对象

# 创建示例数据
data1 <- tibble(
  Year = 2010:2020,
  Sales = c(120, 135, 150, 170, 180, 190, 200, 210, 220, 230, 240)
)

# 创建 tsibble 对象，指定 Year 列为时间索引
ts_data <- tsibble(Year = data1$Year, Sales = data1$Sales, index = Year)

# 查看 tsibble 对象
ts_data

这个示例中，ts_data 就是一个 tsibble 对象，它包含了 Year 作为时间索引，Sales 作为时间序列数据。

2. 处理不规则时间序列数据

# 创建一个不规则时间序列数据
irregular_data <- tsibble(
  Year = c(2010, 2012, 2014, 2015),
  Sales = c(120, 140, 160, 180),
  index = Year)

# 查看不规则时间序列
irregular_data

这个 tsibble 对象包含了不连续的年份，并且能自动处理这些不规则的时间点。

3. 使用键（key）创建多维时间序列数据

# 创建多维时间序列数据，使用 Product 作为键
sales_data <- tibble(
  Product = rep(c("A", "B"), each = 5),
  Year = 2010:2014,
  Sales = c(120, 135, 150, 160, 170, 200, 210, 220, 230, 240)
)

# 创建 tsibble 对象，使用 Product 作为 key，Year 作为时间索引
ts_sales <- tsibble(Product = sales_data$Product, Year = sales_data$Year, Sales = sales_data$Sales, index = Year, key = Product)

# 查看多维时间序列数据
ts_sales

在这个例子中，ts_sales 包含了按 Product 键分组的时间序列数据，每个产品都有独立的时间序列。

tsibble 对象的操作

tsibble 对象支持与 dplyr 等 tidyverse 包的函数结合使用，提供强大的数据操作能力。常见的操作包括筛选、排序、聚合、缺失值处理等。

示例：筛选并排序 tsibble 对象

library(dplyr)

# 选择销售额大于 150 的记录，并按 Year 排序
filtered_data <- ts_data %>%
  filter(Sales > 150) %>%
  arrange(Year)

filtered_data