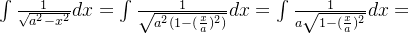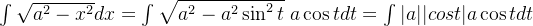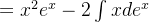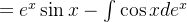1. 第一换元积分法
1. 基础概念:形如![\int f[\phi (x)]{\phi }'(x)dx=\int f[\phi (x)]d\phi (x)\overset{\phi (x)=u}{\rightarrow}\int f(u)du](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNpbnQlMjBmJTVCJTVDcGhpJTIwJTI4eCUyOSU1RCU3QiU1Q3BoaSUyMCU3RCUyNyUyOHglMjlkeCUzRCU1Q2ludCUyMGYlNUIlNUNwaGklMjAlMjh4JTI5JTVEZCU1Q3BoaSUyMCUyOHglMjklNUNvdmVyc2V0JTdCJTVDcGhpJTIwJTI4eCUyOSUzRHUlN0QlN0IlNUNyaWdodGFycm93JTdEJTVDaW50JTIwZiUyOHUlMjlkdQ%3D%3D)
2. 核心思想:通过对被积函数的观察(把被积函数的形式与积分表的积分公式进行比较),把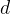
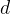
然后进行拼凑,把拼凑的部分看成一个整体,最后利用积分表里的积分公式求解不定积分。
3. 举例说明:
(1)求解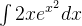
(2)求解
(3)求解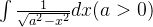
(4)求解
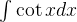
(5)求解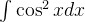
(6)求解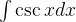

又知:
所以:
(7)求解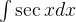
又知:
所以:
即:
2. 第二换元积分法
1. 基本概念:形如![\int f(u)du \overset{u=\phi (x)}{\rightarrow} =\int f[\phi (x)]d\phi (x) =\int f[\phi (x)]{\phi }'(x)dx](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNpbnQlMjBmJTI4dSUyOWR1JTIwJTVDb3ZlcnNldCU3QnUlM0QlNUNwaGklMjAlMjh4JTI5JTdEJTdCJTVDcmlnaHRhcnJvdyU3RCUyMCUzRCU1Q2ludCUyMGYlNUIlNUNwaGklMjAlMjh4JTI5JTVEZCU1Q3BoaSUyMCUyOHglMjklMjAlM0QlNUNpbnQlMjBmJTVCJTVDcGhpJTIwJTI4eCUyOSU1RCU3QiU1Q3BoaSUyMCU3RCUyNyUyOHglMjlkeA%3D%3D)
说明:引入的
,必须是单调的(用到了它的反函数)、可导的(用到了它的导函数) 且
(避免把原被积函数变为0)。
2. 核心思想:通过对被积函数的观察选择相应的替换函数(基本都有规律),然后将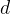
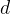
函数的积分转化为简单函数的积分,最终求解出不定积分。
3. 举例说明:
(1)求解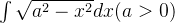
①:需要先确认被积函数的定义域:
。
②:进行替换,令
,要保证替换函数
是单调、可导且
的,取
,则有
,满足被积函数定义域要求。对
求导,可得:
。
因为
,且当
时,
,则:

③:进行回代,根据
可得:
,同时绘制直角三角形,可获得其他三角函数关系式,则:
即:
小贴士:一般遇到根号下含有
的式子,采用
替换。
(2)求解
①:需要先确认被积函数的定义域:
。
②:进行替换,令
,要保证替换函数
是单调、可导且
的,取
,则有
,满足被积函数定义域要求。对
求导,可得:
。
因为
,且当
时,
,则:
③:进行回代,根据
可得:
,同时绘制直角三角形,可获得其他三角函数关系式,则:
根据上述三角形关系可知:
,又知:
,
所以:
即:
小贴士:一般遇到根号下含有
的式子,采用
替换。
(3)求解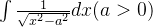
①:需要先确认被积函数的定义域:
。
②:进行替换,令
,要保证替换函数
是单调、可导且
的,取
及
,
则有
,满足被积函数定义域要求。对
求导,可得:
。
对于分区间段的不定积分要分开求解。
当
时,由
可知:
,则
。
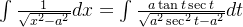
当
时,由
可知:
,则
。
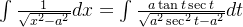
③:进行回代,根据
可得:
,同时绘制直角三角形,可获得其他三角函数关系式,则:
当
时:

当
时,

即:当
时,
当
时,
上述进行整合可得:
小贴士:一般遇到根号下含有
的式子,采用
替换。
(4)求解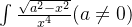
①:需要先确认被积函数的定义域:
。
②:进行替换,令
,要保证替换函数
是单调、可导且
的,取
及
,
则有
,满足被积函数定义域要求。对
求导,可得:
。
对于分区间段的不定积分要分开求解。
当
时,由
可知:
。
当
时,由
可知:
。
③:进行回代:
当
时,
当
时,
备注:最后一步需要注意,开偶数次根号下的内容时不要忘记正负的问题。
(5)求解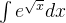
①:需要先确认被积函数的定义域:
。
②:进行替换,令
,即
,要保证替换函数
是单调、可导且
的,取
,
则有
,满足被积函数定义域要求。对
求导,可得:
。
③:进行回代:
3. 分部积分法
1. 基本概念:形如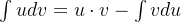
2. 举例说明:
(1)求解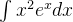
小贴士:被积函数为多项式乘以三角函数或指数函数,此类型一般把三角函数或指数函数作为
。
(2)求解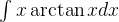
小贴士:被积函数为多项式乘以反三角函数或对数函数,此类型一般把多项式作为
。
(3)求解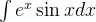
此时,等号左侧所求的式子在等号右侧重复出现了,那么进行移项处理。
整理可得:
小贴士:被积函数为指数函数乘以三角函数,此类型谁作为
都行,只需要多次使用分部积分法,凑出与所求相同的部分,然后再
移项处理,结果+
。
总结:使用分部积分法求解不定积分,不需要特殊记忆哪类函数作为
,哪类函数作为
,只需要明确:
拿到
里面的某项要确保原函数容易求,留在
外面的剩余项要确保导函数容易求,再不行就调换一下嘛。
4. 有理函数的积分
待更新