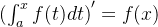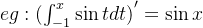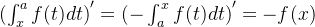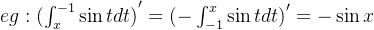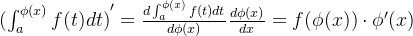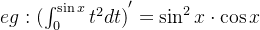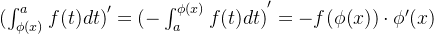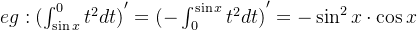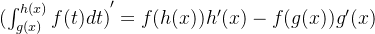1. 定积分的基本概念
1.1 定积分的定义
1. 定义:设函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
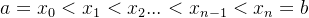
此时每个小区间的长度记作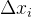
![\xi_{i}\in [x_{i-1},x_{i}]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN4aV8lN0JpJTdEJTVDaW4lMjAlNUJ4XyU3QmktMSU3RCUyQ3hfJTdCaSU3RCU1RA%3D%3D)
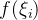
为保证每段

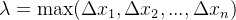
若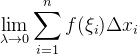
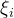
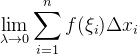

上的定积分,记作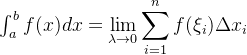
其中:![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)



说明:定积分与被积函数和积分区间有关,与积分变量用什么符号表示无关。
2. 可积条件:
(1)若函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
(2)若函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
3. 几何意义:
(1)如果函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)


![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

所围成的面积。
(2)如果函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)


![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

所围成的面积的相反数。
(3)如果函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
![x\in [a,c]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94%5Cin%20%5Ba%2Cc%5D)

![x\in [c,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94%5Cin%20%5Bc%2Cb%5D)


![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
的定积分为:。
说明:若函数
在闭区间
上的定积分的值为零,那么函数
的图像与闭区间
所围成的面积不一定为零。
1.2 定积分的性质
(1)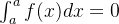
(2)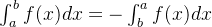
(3)若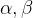
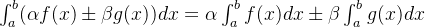
(4)若
。
备注:当
时,上式也是成立的,但前提条件是函数
在对应闭区间上有界且只有有限个间断点。
(5)在闭区间![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

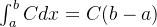
(6)在闭区间![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)


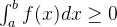
(7)在闭区间![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)


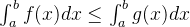
(8)在闭区间![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)

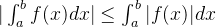
备注:证明出发点:①:
,同时取定积分;②:
。
(9)设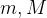

![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
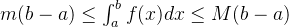
备注:证明出发点:
,同时取定积分。
(10)积分中值定理:设函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
![\xi \in[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN4aSUyMCU1Q2luJTVCYSUyQ2IlNUQ%3D)
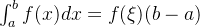
证明:因为函数
在闭区间
上是连续的,则函数
一定存在最大值M与最小值m,即:
对上式两边同时取定积分:
。
因为
,则上式可表达为:
。
因为函数
是连续的,根据介值定理可知:在
上至少存在一点
,使得
,其中
。
所以:
。
备注:上式中
的值称为函数
在闭区间
上的平均值。
2. 变上限积分函数及其导数
1. 变上限积分函数的定义:设函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
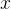
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
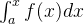

备注:因为定积分与积分变量用什么符号表示无关,故为明确起见,
。
2. 变上限积分函数的导数:
(1)如果函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
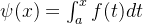
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
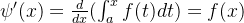
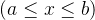
(2)如果函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
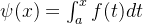

![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
3. 变上限积分函数的导数案例:
(1)
(2)
(3)
(4)
(5)
3. 牛顿 - 莱布尼茨公式
牛顿 - 莱布尼茨公式:若函数
![[a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJhJTJDYiU1RA%3D%3D)
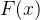

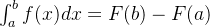
备注:此公式表明:一个连续函数在闭区间
上的定积分等于它的任意一个原函数在闭区间
上的增量。
该公式通常也叫做微积分基本公式。