本文来自https://www.bilibili.com/video/BV1FT4y1E74V,仅为本人学习所用。
文章目录
矩阵和张量
矩阵是一个二维数组,由行和列组成,用于表示线性变换或存储数据;张量是矩阵在高维空间的推广,可以看作是一个多维数组。它可以有零维(标量,如一个单独的数值)、一维(向量,如一个数列)、二维(即矩阵)以及更高维度。
边缘检测
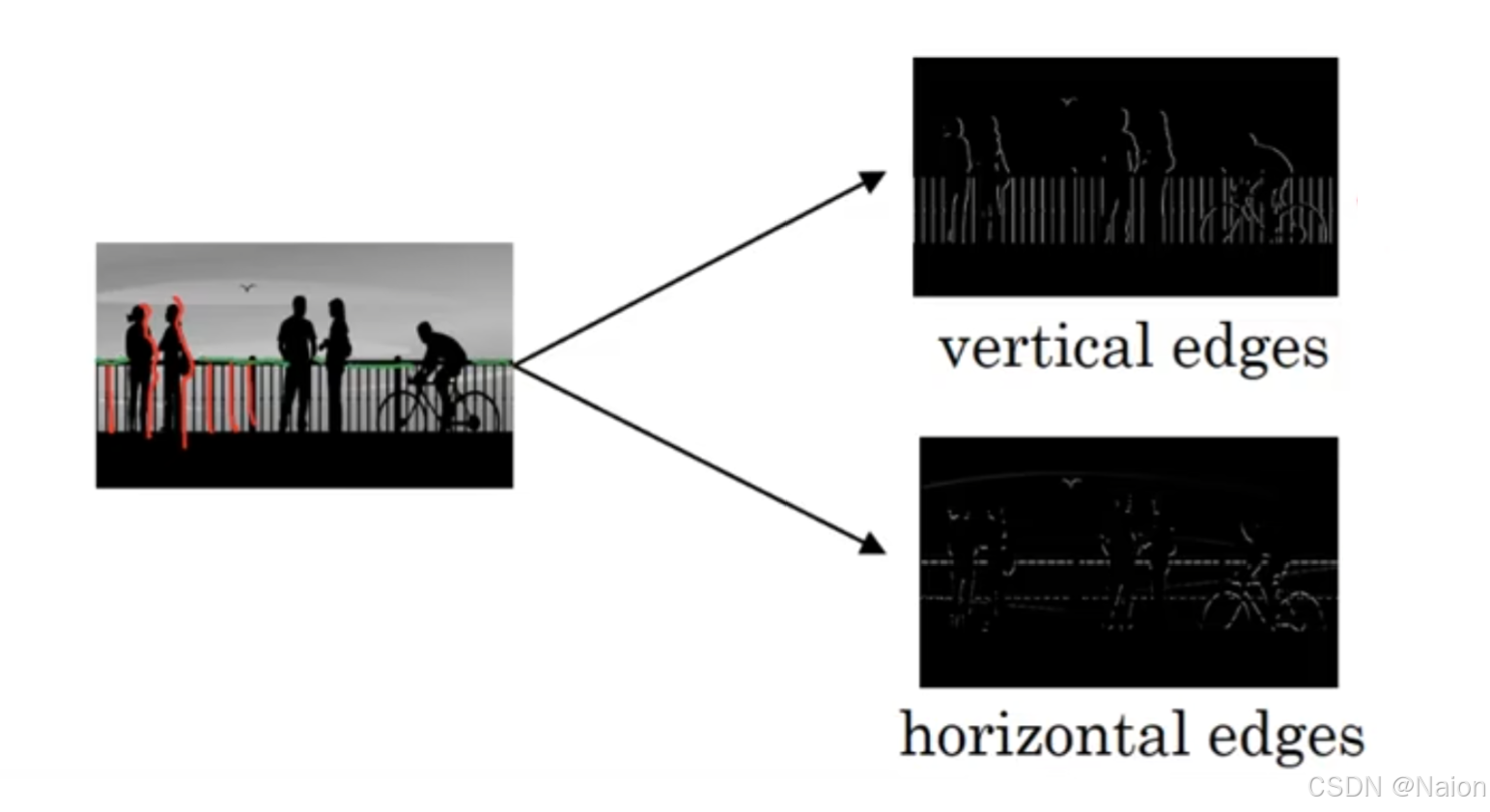
边缘检测是计算机视觉和图像处理中的技术,识别图像中亮度变化剧烈的像素点集合构成的线条(图像边缘),表示了物体、区域的边界。
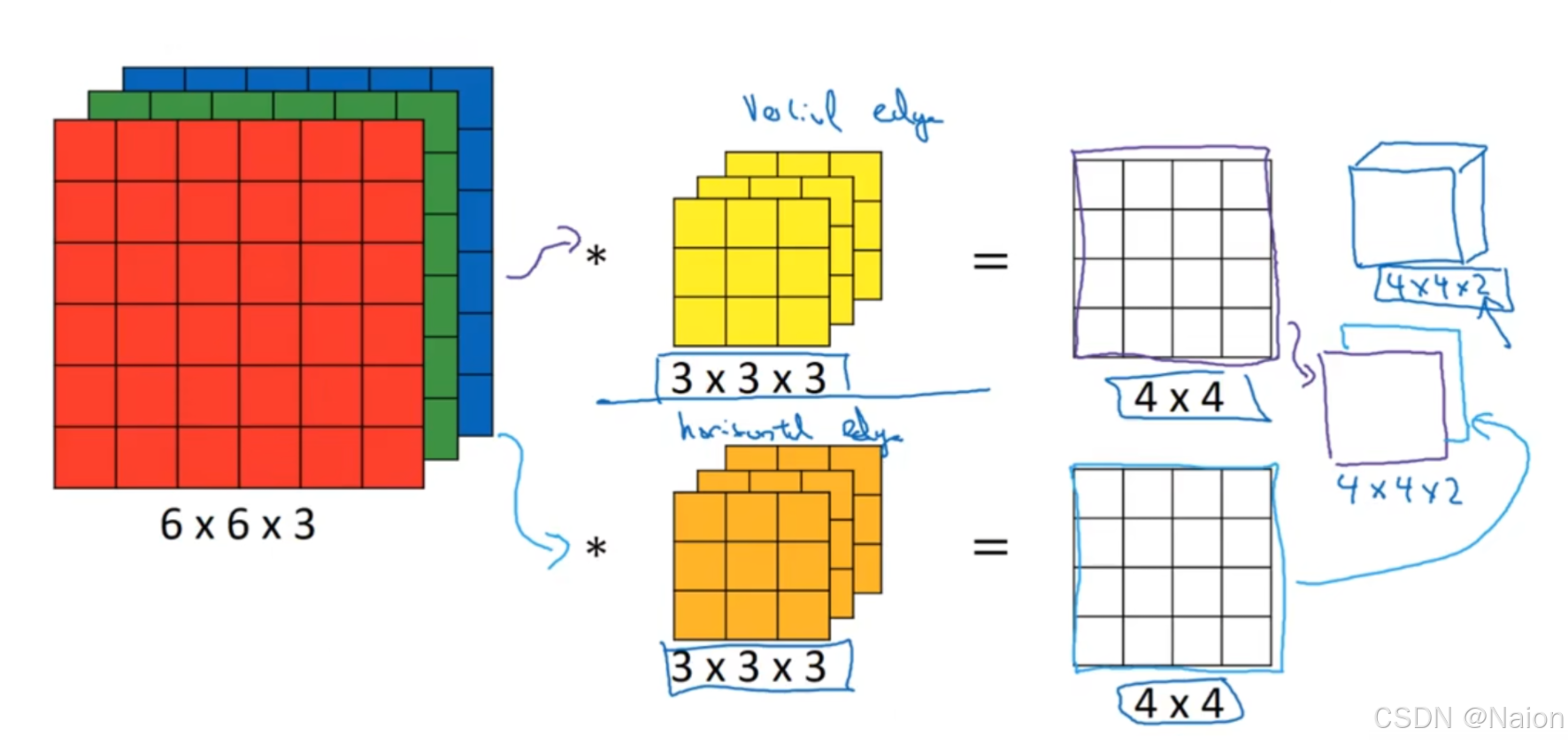
图片展示了边缘检测的结果,左侧是原始图像,右侧上方是检测出的垂直边缘,右侧下方是检测出的水平边缘。
计算方式
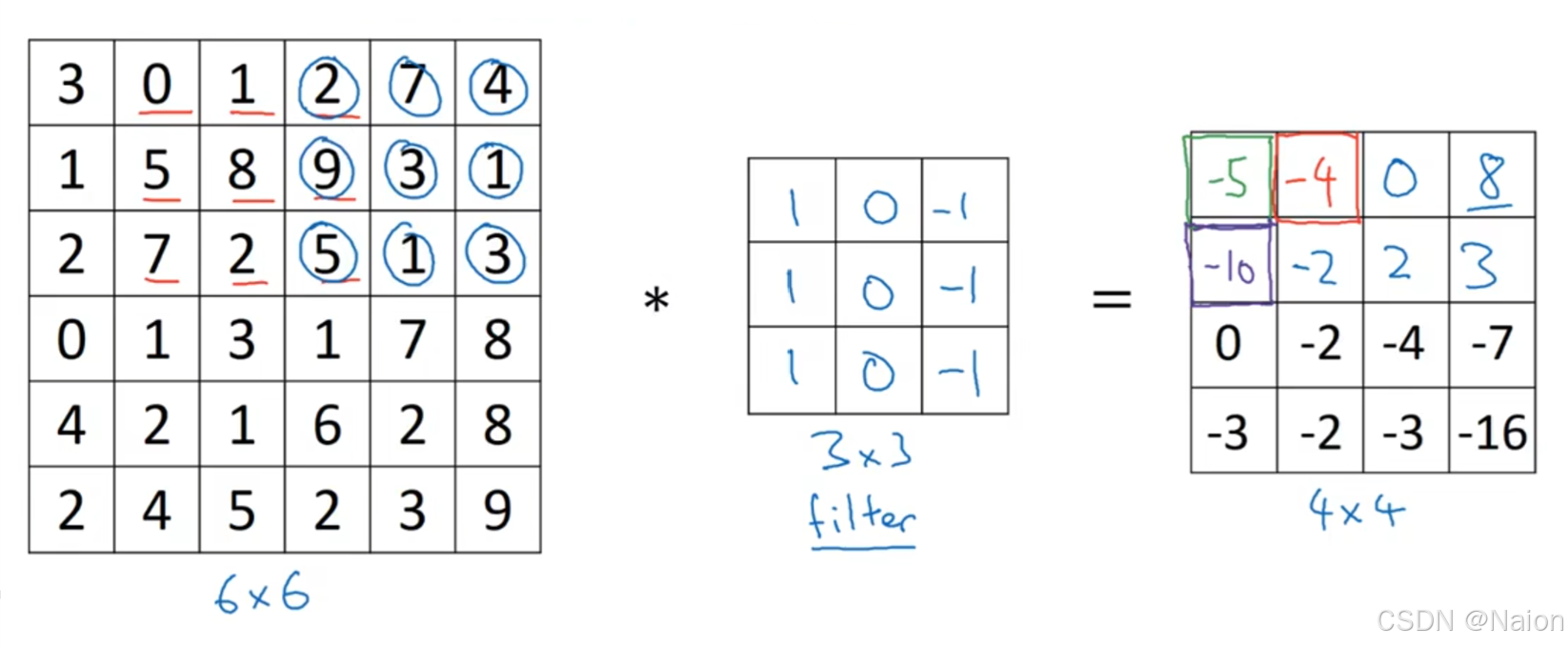
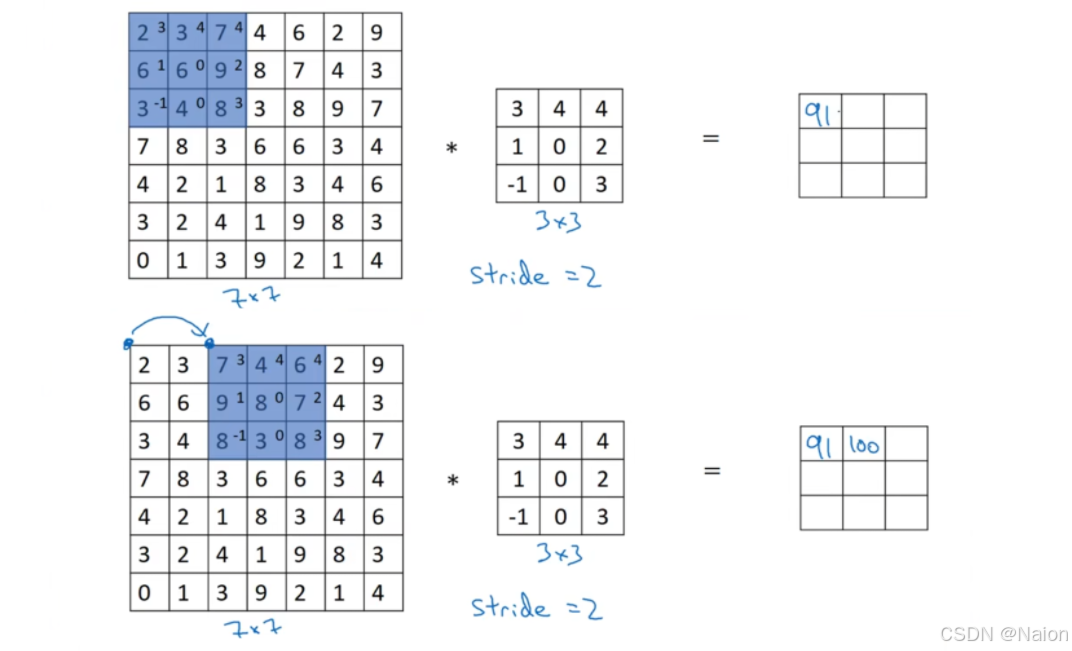
对于这样一个矩阵,计算过程如下:左侧是一个6×6的矩阵,中间是一个3×3的滤波器(核),右侧运算后得到的4×4的结果矩阵。
对于计算结果的第一个元素(-5),滤波器中的值与原矩阵左上角3×3区域(3×1 + 0×0 + 1×(-1) + 1×1 + 5×0 + 8×(-1) + 2×1 + 7×0 + 2×(-1)= -5)对应元素相乘后求和;红色的-4计算结果为滤波器中的值分别与图中红线的一一值相乘后相加(0×1+5×1+7×1+1×0+8×0+2×0+2×(-1)+9×(-1)+5×(-1)= -4);蓝色的8也是相同的算法。依次将滤波器在原矩阵上滑动(每次滑动一个单位),重复上述乘法和求和操作,得到整个结果矩阵。
检测原理
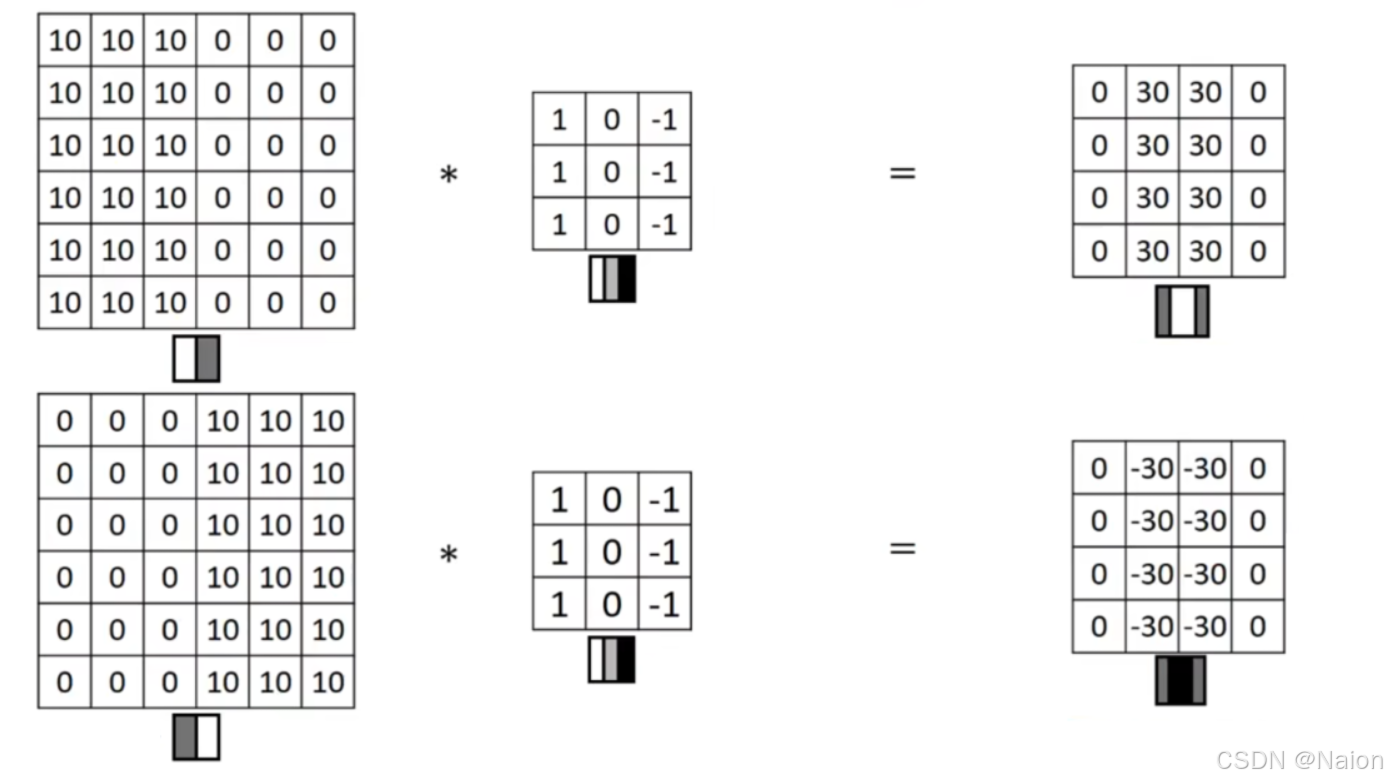
如果将该矩阵看成一张图片,0表示灰色,10表示亮白,在灰色区域和白色区域有一条明显的垂直边缘。过滤器用1表示白,0表示灰,-1表示黑色。经过卷积后,得到44的矩阵,0表示灰,30表示白,可以看到,计算后的结果的中间部分有明显的白色区域,表示66矩阵的垂直边缘。
如果将图像反转,得到中间是黑色区域的输出矩阵。与由白(亮)向暗不同,反转的输出结果展示了由暗向亮(灰色相对于黑色更亮)。如果不在乎这两者的区别,可以为结果加绝对值。
Valid卷积和Same卷积
上述的6*6的矩阵,经过3*3的过滤器后,得到4*4的输出矩阵。设原矩阵是 n × n n\times n n×n的大小,过滤器是 f × f f \times f f×f的大小,输出结果就是 ( n − f + 1 ) × ( n − f + 1 ) (n-f+1) \times (n-f+1) (n−f+1)×(n−f+1)大小的矩阵,这样做,每次卷积都使得图片进一步缩小;同时,输入矩阵中间的核心像素被频繁计算,而角落或者边缘像素在输出时被使用较少。
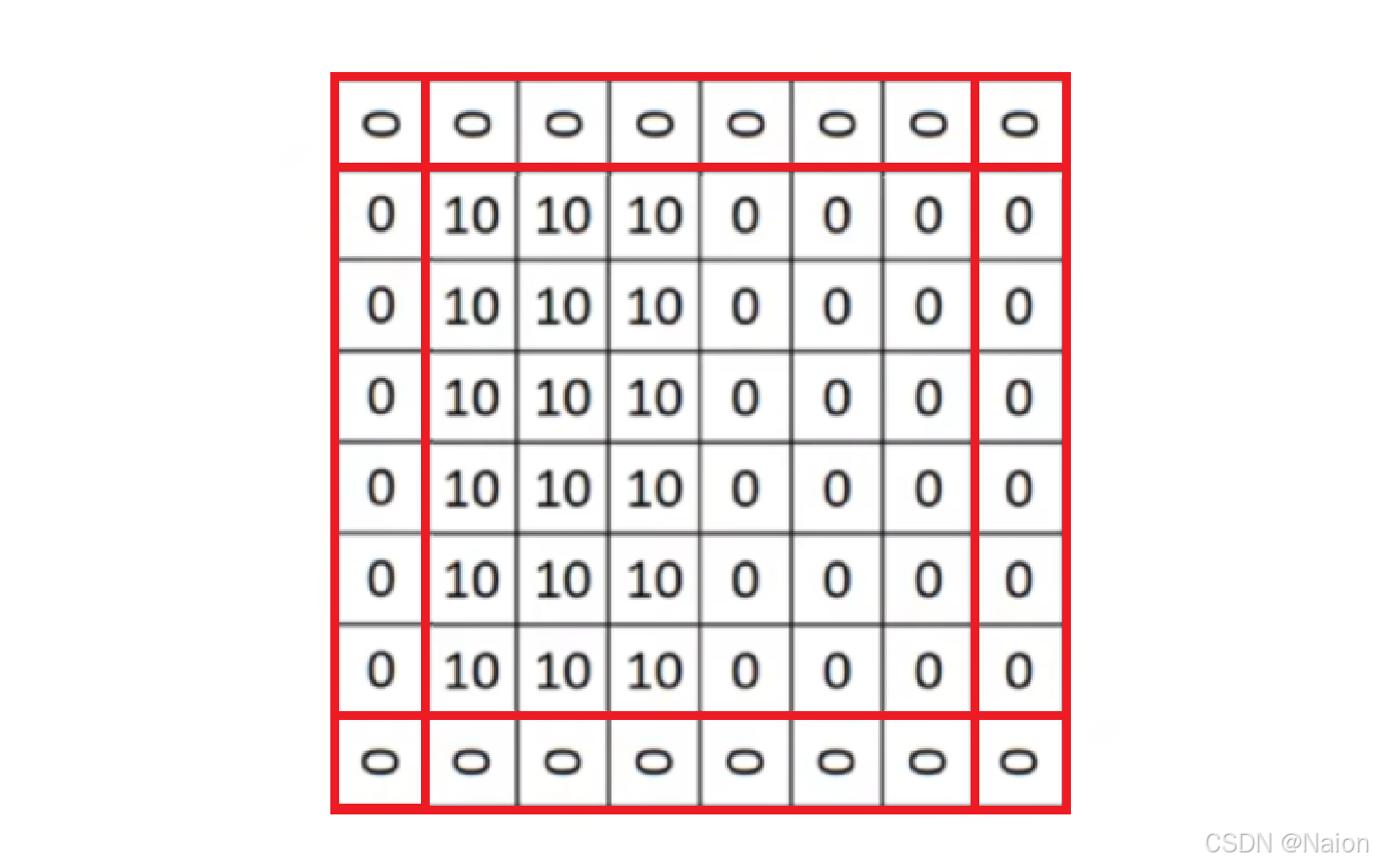
因此,在使用卷积之前,需要将图片做填充(Padding),将6*6的矩阵最外层在填充一层像素,变成8*8的矩阵。填充的数字可以是0填充。
大小为
(
n
+
2
p
−
f
+
1
)
×
(
n
+
2
p
−
f
+
1
)
(n+2p-f+1) \times (n+2p-f+1)
(n+2p−f+1)×(n+2p−f+1)其中,
p
p
p是填充的层数,本例中填充了一层。
上面两种是不同的卷积方式:
- Valid卷积:不进行填充的卷积操作。若输入数据尺寸为 n × n n \times n n×n ,滤波器(卷积核)尺寸为 f × f f \times f f×f ,那么输出尺寸为 ( n − f + 1 ) × ( n − f + 1 ) (n - f + 1)\times(n - f + 1) (n−f+1)×(n−f+1) 。
- Same卷积:使输出尺寸和输入尺寸相同的卷积。需要对输入进行填充操作,设填充层数为 p p p ,则输出尺寸为 ( n + 2 p − f + 1 ) × ( n + 2 p − f + 1 ) (n + 2p - f + 1)\times(n + 2p - f + 1) (n+2p−f+1)×(n+2p−f+1) 。为使输出尺寸等于输入尺寸 n n n ,即 n + 2 p − f + 1 = n n+2p - f + 1=n n+2p−f+1=n ,可推出 p = f − 1 2 p=\frac{f - 1}{2} p=2f−1 ( f f f 通常为奇数,否则图像将不对称,这也是过滤器大小选择奇数的原因) 。
Valid卷积会缩小特征图尺寸,Same卷积可保持特征图尺寸不变。
卷积步长
如果将卷积步长
s
=
2
s=2
s=2:
计算后的输出矩阵大小为
⌊
n
+
2
p
−
f
s
+
1
⌋
×
⌊
n
+
2
p
−
f
s
+
1
⌋
\left \lfloor\frac{n + 2p - f }{s}+1\right \rfloor\times\left \lfloor\frac{n + 2p - f }{s}+1\right \rfloor
⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋
三维卷积
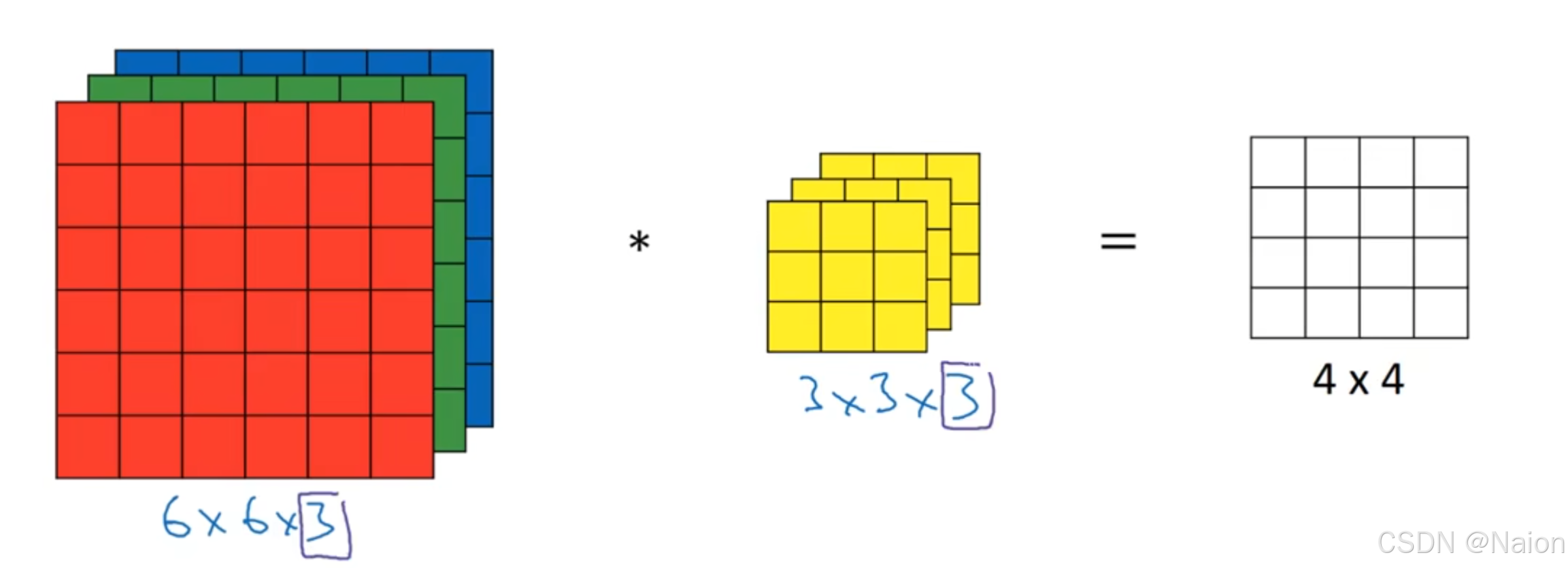
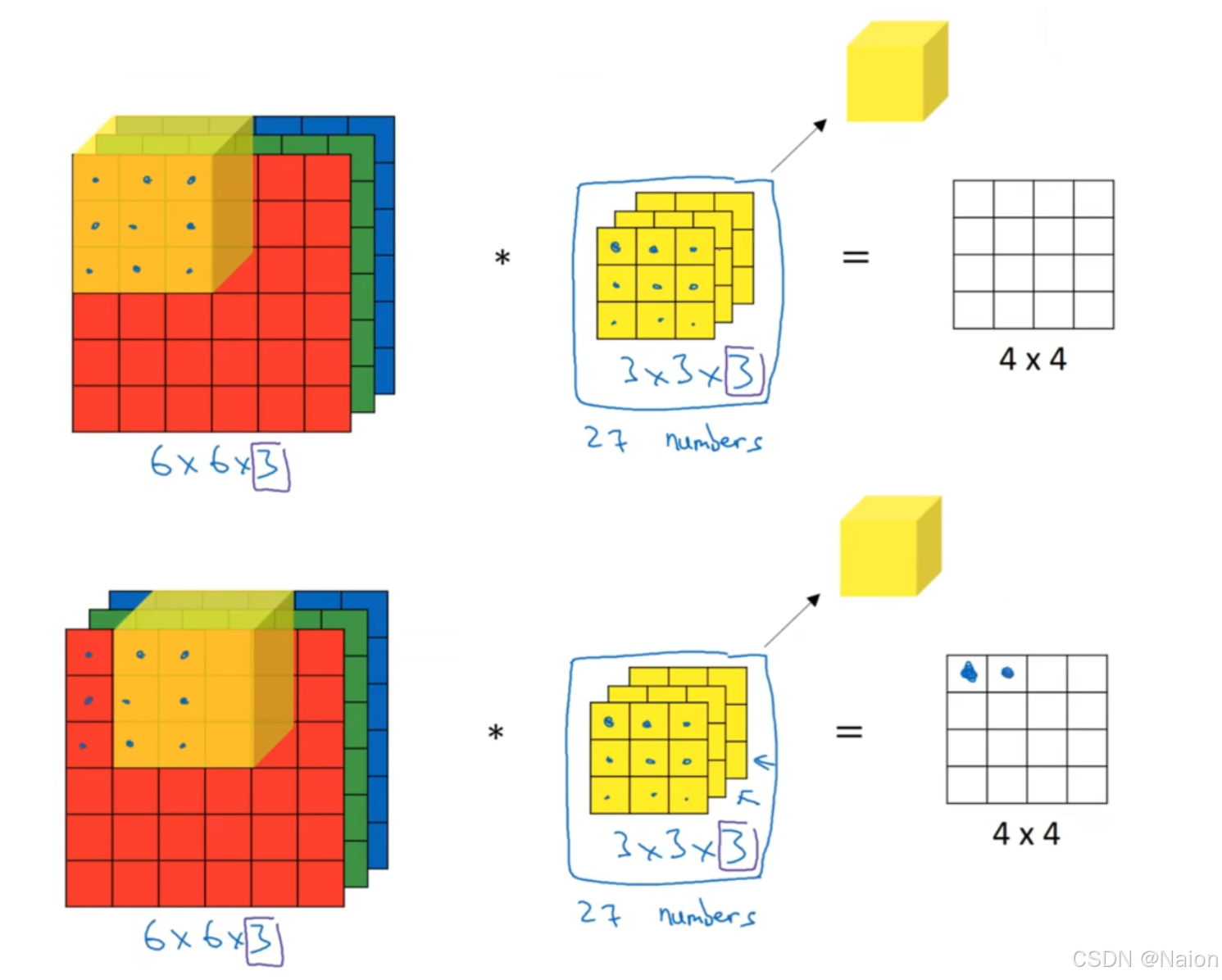
如果是三维的卷积,对于6*6*3,规定第一个6是高,第二个6是宽度,第三个3是通道数,要求三维输入张量的通道数必须与过滤器的通道数相同。最后得到4*4*1的输出张量。
类似二维的卷积计算,三维的卷积计算时,首先过滤器(有27个参数)与三维输入张量分别相乘后在相加,得到的数填在输出张量中,然后继续移动过滤器,重复以上的计算。
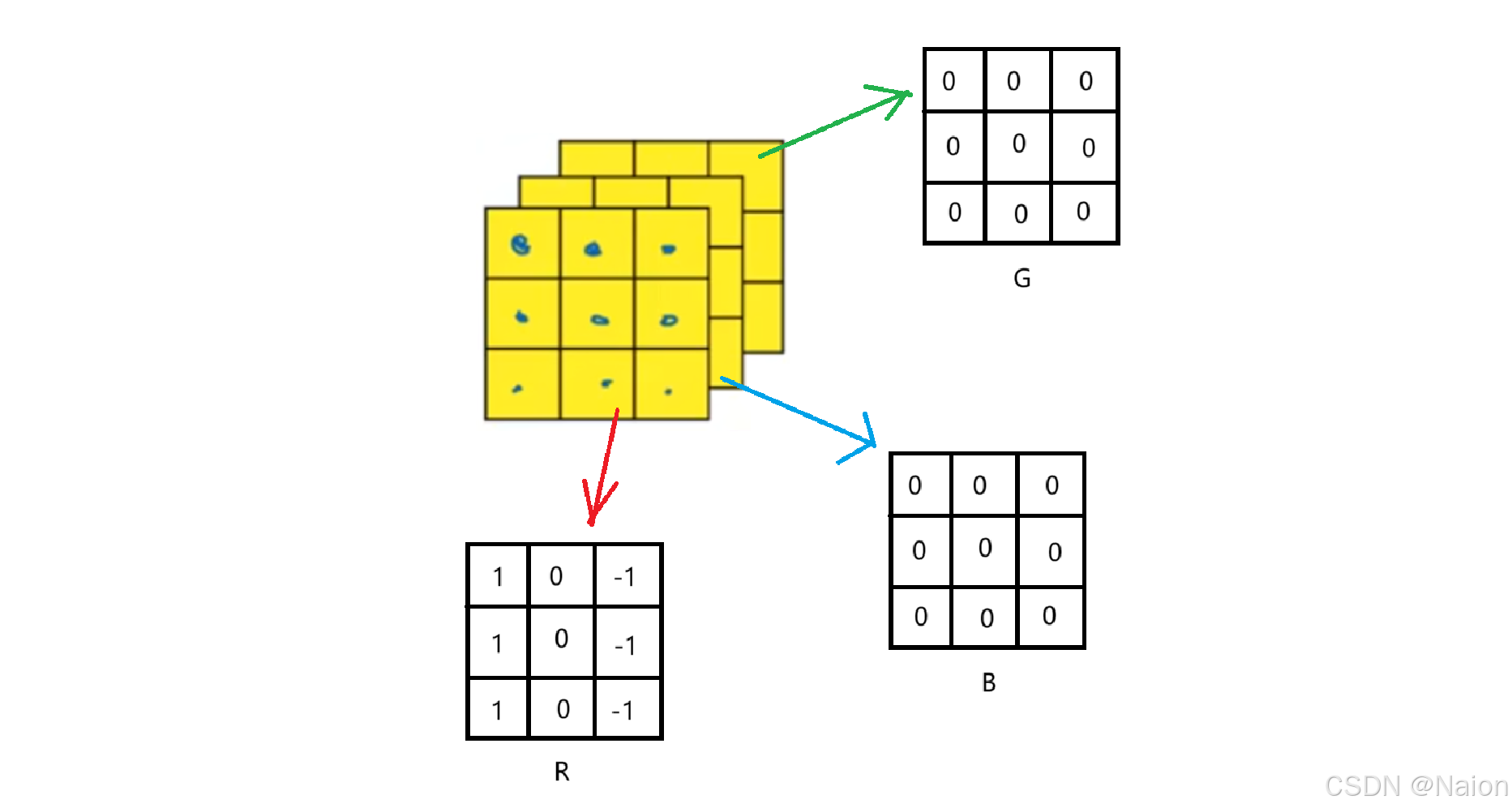
如果只是想计算红色的边缘信息,将过滤器的第一个通道设置1,0,-1,其他通道设置为0即可。
如果有多个过滤器,输入是一个尺寸为
6
×
6
×
3
6×6×3
6×6×3的三维张量:
有两组
3
×
3
×
3
3×3×3
3×3×3的过滤器,每个过滤器都是
3
×
3
×
3
3×3×3
3×3×3的大小,经过卷积运算后,得到两个尺寸为
4
×
4
4×4
4×4的的输出张量,输出一个大小为
4
×
4
×
2
4×4×2
4×4×2的张量。
如果输入为 n × n × n c n×n×n_c n×n×nc( n n n是特征图边长, n c n_c nc是通道数),过滤器为 f × f × n c f×f×n_c f×f×nc( f f f是过滤器边长, n c n_c nc是通道数),经过卷积运算后,输出尺寸为 ( n − f + 1 ) × ( n − f + 1 ) × n c ′ (n - f + 1)×(n - f + 1)×n_c' (n−f+1)×(n−f+1)×nc′,其中 n c ′ n_c' nc′是过滤器的数量。本例的 n = 6 n = 6 n=6, f = 3 f = 3 f=3, n c = 3 n_c = 3 nc=3, n c ′ = 2 n_c' = 2 nc′=2,输出尺寸为 4 × 4 × 2 4×4×2 4×4×2。
单层卷积网络
如果使用线性函数
z
=
w
x
+
b
z=wx+b
z=wx+b和激活函数
a
=
g
(
z
)
a=g(z)
a=g(z)。输入的
6
×
6
×
3
6×6×3
6×6×3的张量,记为
a
[
0
]
a^{[0]}
a[0],两个大小为
3
×
3
×
3
3×3×3
3×3×3的卷积核(过滤器),记为
W
[
1
]
W^{[1]}
W[1]。分别与输入张量
a
[
0
]
a^{[0]}
a[0]进行卷积运算
z
[
1
]
=
W
[
1
]
a
[
0
]
+
b
[
1
]
z^{[1]} = W^{[1]}a^{[0]} + b^{[1]}
z[1]=W[1]a[0]+b[1],其中
z
[
1
]
z^{[1]}
z[1]是线性变换后的结果,
b
[
1
]
b^{[1]}
b[1]是偏置项,
b
1
b_1
b1和
b
2
b_2
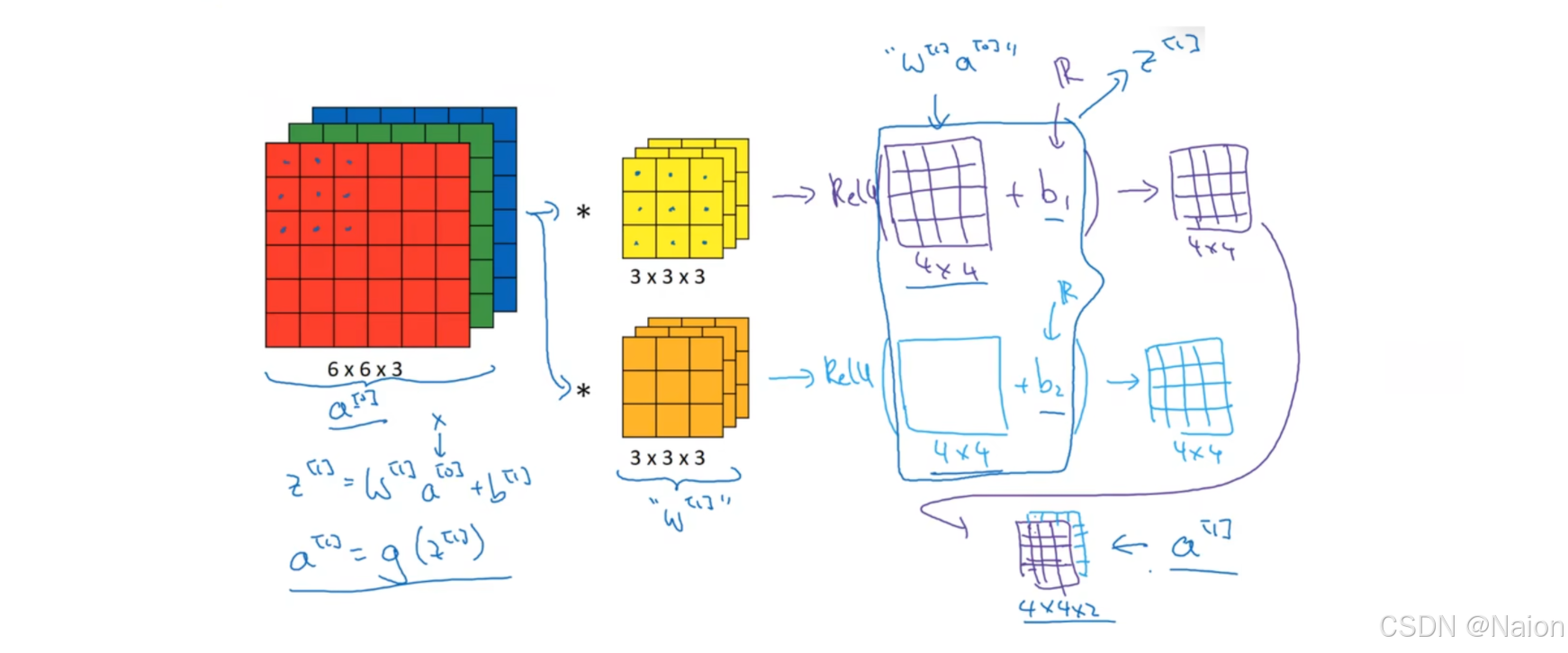
b2分别对应两组卷积核的运算结果。对线性变换结果
z
[
1
]
z^{[1]}
z[1]应用ReLU激活函数,记为
g
(
z
)
g(z)
g(z),即
a
[
1
]
=
g
(
z
[
1
]
)
a^{[1]} = g(z^{[1]})
a[1]=g(z[1])。最终得到一个大小为
4
×
4
×
2
4×4×2
4×4×2的输出张量
a
[
1
]
a^{[1]}
a[1]。
总结
符号定义
- f [ l ] f^{[l]} f[l]:表示第 l l l层卷积层中过滤器(卷积核)的大小。
- p [ l ] p^{[l]} p[l]:第 l l l层的填充数量。
- s [ l ] s^{[l]} s[l]:第 l l l层的步长。
- n c [ l ] n_c^{[l]} nc[l]:第 l l l层中过滤器的数量。
输入输出维度
- 输入:维度为 n H [ l − 1 ] × n W [ l − 1 ] × n c [ l − 1 ] n_H^{[l - 1]}×n_W^{[l - 1]}×n_c^{[l - 1]} nH[l−1]×nW[l−1]×nc[l−1],其中 n H [ l − 1 ] n_H^{[l - 1]} nH[l−1]和 n W [ l − 1 ] n_W^{[l - 1]} nW[l−1]分别是第 l − 1 l - 1 l−1层输出特征图的高度和宽度, n c [ l − 1 ] n_c^{[l - 1]} nc[l−1]是是第 l − 1 l - 1 l−1层通道数。
- 输出:维度为 n H [ l ] × n W [ l ] × n c [ l ] n_H^{[l]}×n_W^{[l]}×n_c^{[l]} nH[l]×nW[l]×nc[l],其中 n H [ l ] n_H^{[l]} nH[l]和 n W [ l ] n_W^{[l]} nW[l]可由公式 n H [ l ] = n W [ l ] = ⌊ n H ( W ) [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_H^{[l]}=n_W^{[l]}=\lfloor\frac{n_{H(W)}^{[l - 1]} + 2p^{[l]}-f^{[l]}}{s^{[l]}}+1\rfloor nH[l]=nW[l]=⌊s[l]nH(W)[l−1]+2p[l]−f[l]+1⌋计算得出, n c [ l ] n_c^{[l]} nc[l]为该层过滤器数量。
其他参数维度
- 激活值:运用偏差和非线性函数后,本层的输出 a [ l ] a^{[l]} a[l]的维度是 n H [ l ] × n W [ l ] × n c [ l ] n_H^{[l]}×n_W^{[l]}×n_c^{[l]} nH[l]×nW[l]×nc[l]。如果考虑批量梯度下降或者mini-batch,对于 m m m个样本,则 A [ l ] A^{[l]} A[l]维度为 m × n H [ l ] × n W [ l ] × n c [ l ] m×n_H^{[l]}×n_W^{[l]}×n_c^{[l]} m×nH[l]×nW[l]×nc[l]。
- 权重: W [ l ] W^{[l]} W[l]的维度是 f [ l ] × f [ l ] × n c [ l − 1 ] × n c [ l ] f^{[l]}×f^{[l]}×n_c^{[l - 1]}×n_c^{[l]} f[l]×f[l]×nc[l−1]×nc[l]。
- 偏置: b [ l ] b^{[l]} b[l]数量等于该层过滤器数量 n c [ l ] n_c^{[l]} nc[l],或者使用的维度是 ( 1 , 1 , 1 , n c [ l ] ) (1,1,1,n_c^{[l]}) (1,1,1,nc[l])大小的四维张量。
举例
输入数据维度为
39
×
39
×
3
39×39×3
39×39×3,其中
39
×
39
39×39
39×39是图片大小,
3
3
3表示通道数。
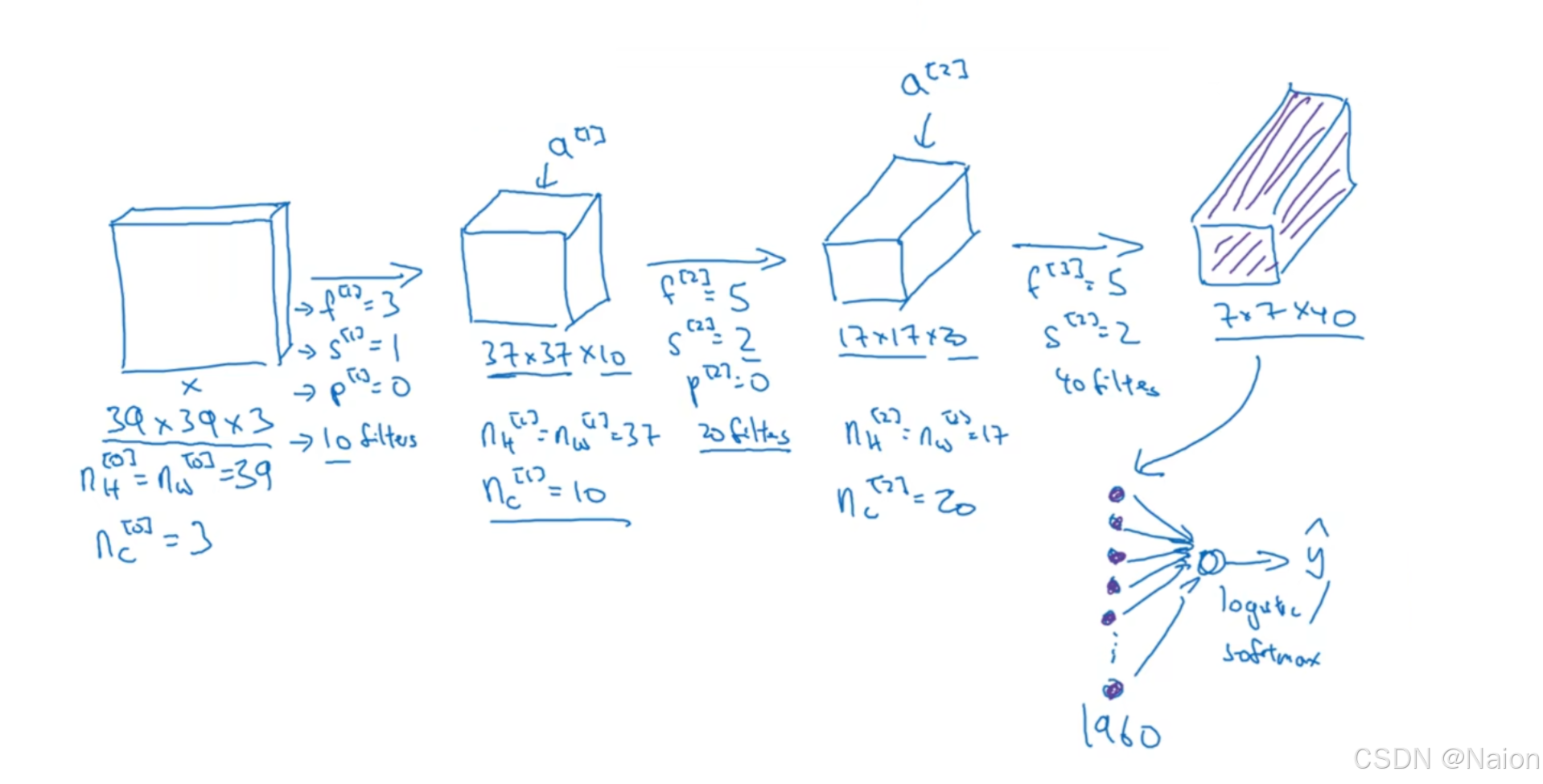
在第一层卷积,过滤器大小 f [ 1 ] = 3 f^{[1]} = 3 f[1]=3,步长 s [ 1 ] = 1 s^{[1]} = 1 s[1]=1,填充 p [ 1 ] = 0 p^{[1]} = 0 p[1]=0,过滤器数量 n c [ 1 ] = 10 n_c^{[1]} = 10 nc[1]=10。根据公式 n H [ l ] = n W [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_H^{[l]}=n_W^{[l]}=\lfloor\frac{n_H^{[l - 1]} + 2p^{[l]}-f^{[l]}}{s^{[l]}}+1\rfloor nH[l]=nW[l]=⌊s[l]nH[l−1]+2p[l]−f[l]+1⌋,可得 n H [ 1 ] = n W [ 1 ] = ⌊ 39 + 2 × 0 − 3 1 + 1 ⌋ = 37 n_H^{[1]}=n_W^{[1]}=\lfloor\frac{39+ 2×0 - 3}{1}+1\rfloor = 37 nH[1]=nW[1]=⌊139+2×0−3+1⌋=37,输出维度为 37 × 37 × 10 37×37×10 37×37×10。
第二层卷积,过滤器大小 f [ 2 ] = 5 f^{[2]} = 5 f[2]=5,步长 s [ 2 ] = 2 s^{[2]} = 2 s[2]=2,填充 p [ 2 ] = 0 p^{[2]} = 0 p[2]=0,过滤器数量 n c [ 2 ] = 20 n_c^{[2]} = 20 nc[2]=20,可得 n H [ 2 ] = n W [ 2 ] = ⌊ 37 + 2 × 0 − 5 2 + 1 ⌋ = 17 n_H^{[2]}=n_W^{[2]}=\lfloor\frac{37+ 2×0 - 5}{2}+1\rfloor = 17 nH[2]=nW[2]=⌊237+2×0−5+1⌋=17,输出维度为 17 × 17 × 20 17×17×20 17×17×20。
第三层卷积,过滤器大小 f [ 3 ] = 5 f^{[3]} = 5 f[3]=5,步长 s [ 3 ] = 2 s^{[3]} = 2 s[3]=2,填充 p [ 3 ] = 0 p^{[3]} = 0 p[3]=0,过滤器数量 n c [ 3 ] = 40 n_c^{[3]} = 40 nc[3]=40,可得 n H [ 3 ] = n W [ 3 ] = ⌊ 17 + 2 × 0 − 5 2 + 1 ⌋ = 7 n_H^{[3]}=n_W^{[3]}=\lfloor\frac{17+ 2×0 - 5}{2}+1\rfloor = 7 nH[3]=nW[3]=⌊217+2×0−5+1⌋=7,输出维度为 7 × 7 × 40 7×7×40 7×7×40。
将 7 × 7 × 40 7×7×40 7×7×40的输出展平后连接到全连接层,最终通过逻辑回归(logistic)或Softmax函数得到输出 y y y ,全连接层输入特征为 7 × 7 × 40 = 1960 7×7×40 = 1960 7×7×40=1960。
一个典型的卷积网络有三层:卷积层(Conv)、池化层(pool)和全连接层(FC)。
池化层
池化层对输入的特征图进行采样操作,通过在局部区域内进行聚合计算,改变特征图的尺寸和特征表示。
最大池化在特征图的局部区域内选取最大值作为该区域池化后的输出值。
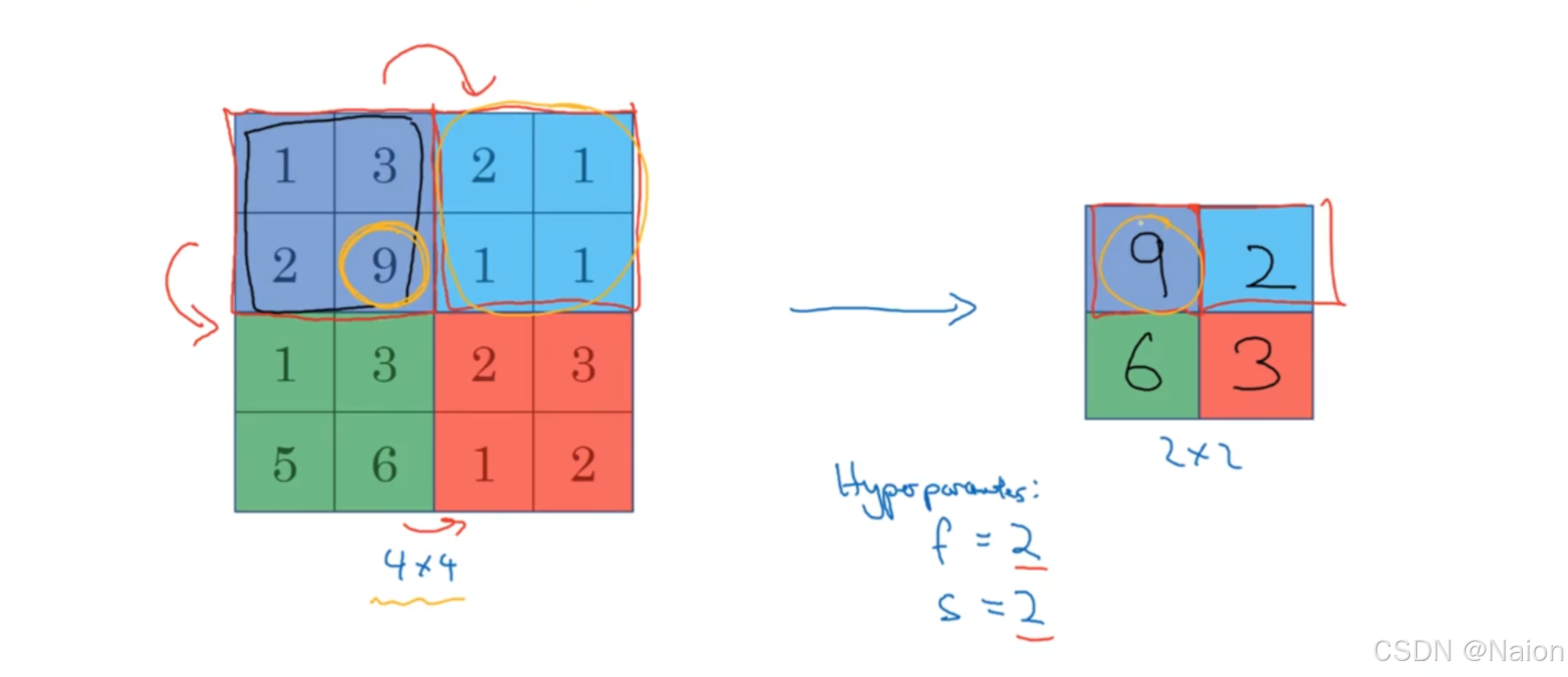
设定一个池化窗口(如 2 × 2 2×2 2×2、 3 × 3 3×3 3×3)和步长(stride),池化窗口按照步长在特征图上滑动,每到一个位置,取窗口内的最大值作为输出特征图对应位置的值。例如,对于一个 2 × 2 2×2 2×2的池化窗口和步长为2的最大池化操作,它会将输入特征图划分为不重叠的 2 × 2 2×2 2×2区域,每个区域输出一个最大值。
最大池化减少特征图的空间尺寸(高度和宽度),降低计算量和模型参数数量,加快训练速度。例如,将一个 32 × 32 32×32 32×32的特征图通过 2 × 2 2×2 2×2步长为2的最大池化,尺寸变为 16 × 16 16×16 16×16。同时保留局部区域内的最大值,意味着保留了该区域最显著的特征,对特征进行了筛选和强化。
超参数 f f f和 s s s最常见的取值是2和2。
示例
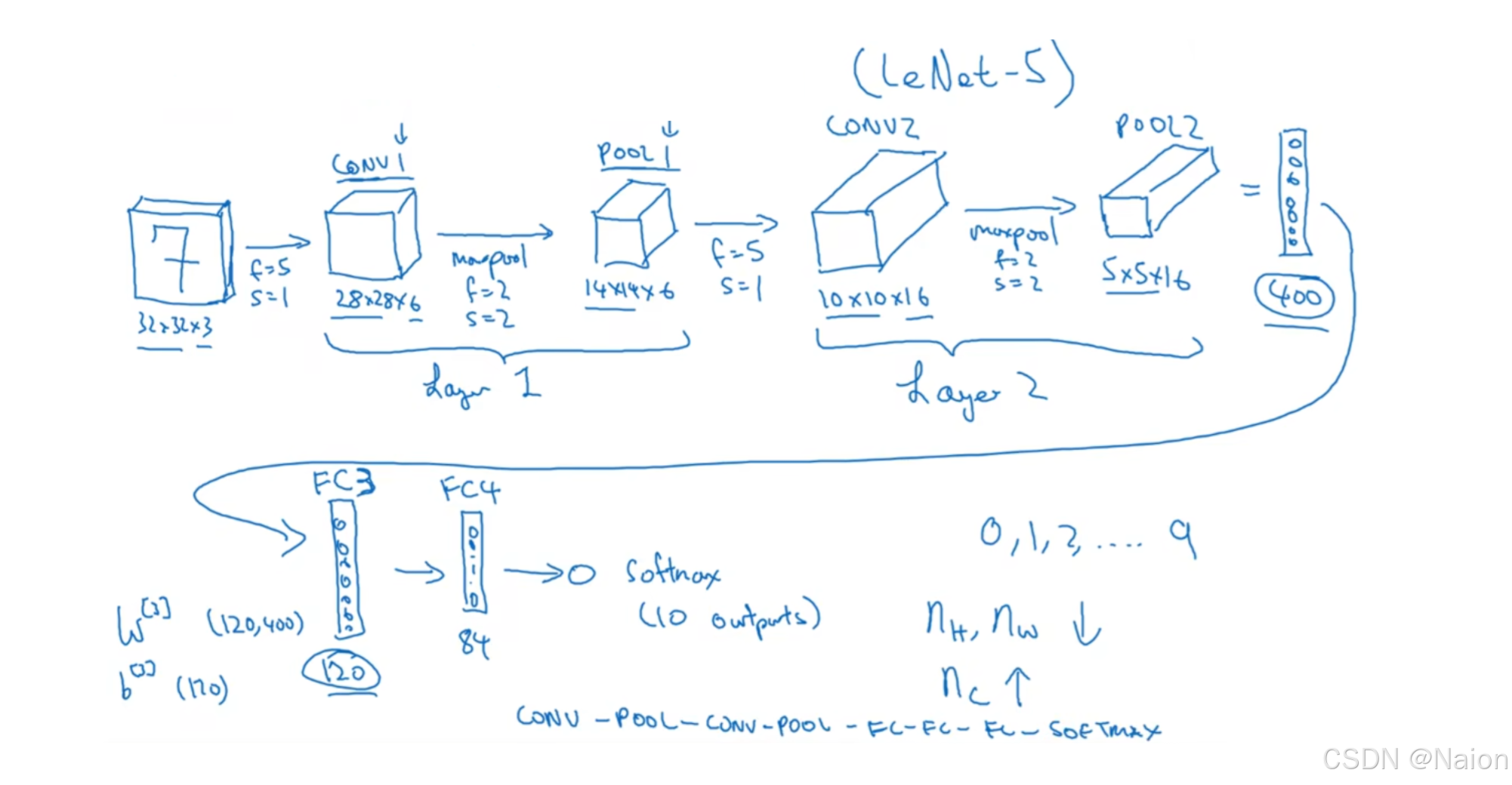
卷积神经网络加上池化层后,模型如下:
输入层
输入是一个尺寸为 32 × 32 × 3 32×32×3 32×32×3的图像,其中 32 × 32 32×32 32×32是图像的空间尺寸, 3 3 3表示通道数。
第一层卷积 - 池化
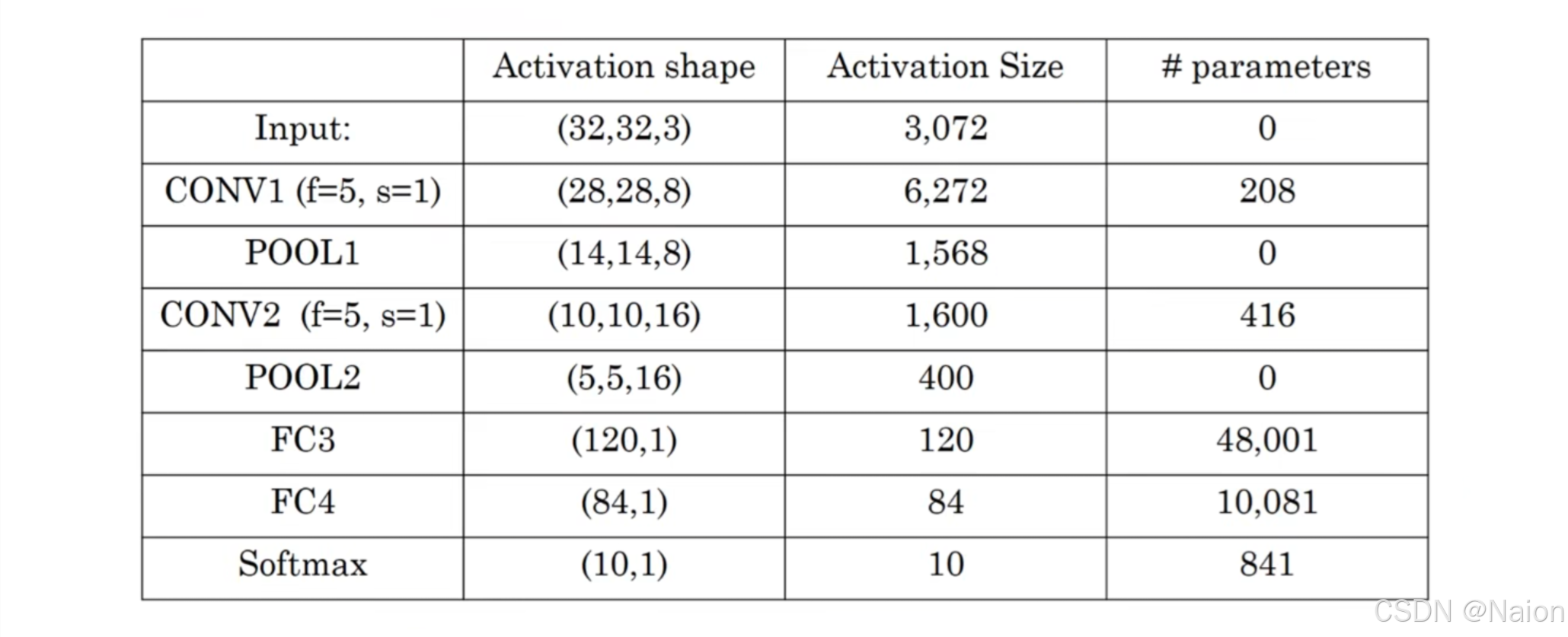
- 卷积层(CONV1):使用大小为 5 × 5 5×5 5×5( f = 5 f = 5 f=5)、步长为 1 1 1( s = 1 s = 1 s=1)的过滤器,数量为 6 6 6( n c = 6 n_c = 6 nc=6)。根据公式 n H [ l ] = n W [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_H^{[l]}=n_W^{[l]}=\lfloor\frac{n_H^{[l - 1]} + 2p^{[l]}-f^{[l]}}{s^{[l]}}+1\rfloor nH[l]=nW[l]=⌊s[l]nH[l−1]+2p[l]−f[l]+1⌋(假设填充 p = 0 p = 0 p=0),输出特征图尺寸为 28 × 28 × 6 28×28×6 28×28×6。
- 池化层(POOL1):采用最大池化,池化窗口大小为 2 × 2 2×2 2×2( f = 2 f = 2 f=2),步长为 2 2 2( s = 2 s = 2 s=2),输出特征图尺寸变为 14 × 14 × 6 14×14×6 14×14×6。
第二层卷积 - 池化
- 卷积层(CONV2):使用大小为 5 × 5 5×5 5×5( f = 5 f = 5 f=5)、步长为 1 1 1( s = 1 s = 1 s=1)的过滤器,数量为 16 16 16( n c = 16 n_c = 16 nc=16),输出特征图尺寸为 10 × 10 × 16 10×10×16 10×10×16。
- 池化层(POOL2):同样是最大池化,池化窗口大小为 2 × 2 2×2 2×2( f = 2 f = 2 f=2),步长为 2 2 2( s = 2 s = 2 s=2),输出特征图尺寸变为 5 × 5 × 16 5×5×16 5×5×16,展平后为 400 400 400个神经元。
全连接层
- FC3层:权重矩阵 W [ 3 ] W^{[3]} W[3]维度为 ( 120 , 400 ) (120,400) (120,400),偏置 b [ 3 ] b^{[3]} b[3]维度为 ( 120 ) (120) (120),输出 120 120 120个神经元。
- FC4层:接着连接到有 84 84 84个神经元的全连接层。
输出层
通过Softmax函数,输出
10
10
10个类别(对应数字
0
−
9
0 - 9
0−9)的概率分布,用于图像分类。
为什么使用卷积
- 参数共享:在图像某一部分有用的特征检测器(如垂直边缘检测器),在图像的另一部分可能同样有用。同一个卷积核在对输入数据的不同位置进行卷积运算时,权重固定不变。这大大减少了模型需要学习的参数数量,降低了模型的复杂度。
- 在卷积神经网络的每一层中,每个输出值仅依赖于少量的输入值。卷积核在进行卷积操作时,每次只与输入数据的一个局部区域进行交互,而不是与整个输入数据的所有元素相连。比如一个3×3的卷积核在图像上滑动进行卷积运算,对于输出特征图上的每个点,它只依赖于输入图像中对应3×3区域内的像素值,而非整个图像的像素,体现了连接的稀疏性。这种特性使得模型的参数数量大幅减少,计算量降低,同时也有助于提取数据的局部特征 。