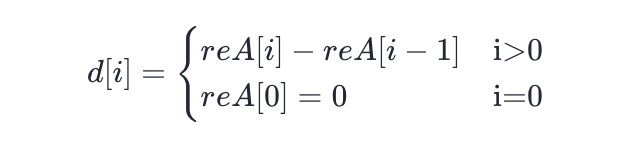引入
内容不做赘述,这道题如果用模拟的方式是会超时的:也就是在循环的过程中,对于K大小的数组,每一位与1取异或。
可以看到这样的效率很低,其复杂度为O(KN)。
更好的办法是用差分数组。
差分数组
如果给你一个包含5000万个元素的数组,然后会有频繁区间修改操作,那什么是频繁的区间修改操作呢?比如让第1个数到第1000万个数每个数都加上1,而且这种操作时频繁的。
此时你应该怎么做?很容易想到的是,从第1个数开始遍历,一直遍历到第1000万个数,然后每个数都加上1,如果这种操作很频繁的话,那这种暴力的方法在一些实时的系统中可能就拉跨了。
比如我们现在有一个数组reA,reA={0,2,5,4,9,7,10,0},差分数组的计算公式为:
这时候,如果构造差分数组:
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| arr | 0 | 2 | 5 | 4 | 9 | 7 | 10 | 0 |
| diff | 0 | 2 | 3 | -1 | 5 | -2 | 3 | -10 |
构造差分数组的效果,我们可以看下面一个例子,比如对于区间[1-4]整体加上5,除开暴力的加上去,差分数组只需要在diff[1]上加5,在diff[5]上减去5:
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| arr | 0 | 2 | 5 | 4 | 9 | 7 | 10 | 0 |
| 暴力 | 0 | 2+5 | 5+5 | 4+5 | 9+5 | 7 | 10 | 0 |
| diff | 0 | 2+5 | 3 | -1 | 5 | -2-5 | 3 | -10 |
可以看到,无论区间K有多大,暴力的复杂度是O(K),而差分的复杂度是O(2)。
现在来看真实的计算:
如何根据差分数组diff来推测reA中某一个位置的值呢?
比如求reA[1],我们知道,reA[1]-reA[0]=diff[1]=>reA[1]=diff[1]+reA[0]=>reA[1]=2+5+0=7。
现在就知道差分数组的作用了,就是以空间换时间。
题解
我们用差分数组diff来表示两个数字之间翻转次数的差值。由于第i位的0需要翻转成为1,那么我们需要将diff[i]++,将diff[i+k]--来表示差分的值。
另外,由于diff[i]的值有变化,对于某一位i的值,不能简单的用原先的0或者1来判断了,需要与diff[i]结合起来。
import java.util.*;
class Solution {
public int minKBitFlips(int[] nums, int k) {
int[] diff = new int[nums.length+1];
int revCnt = 0;
int count = 0;
for (int i = 0; i < nums.length; i++) {
revCnt += diff[i];
if (((revCnt + nums[i]) & 1) == 0) {
if (i + k > nums.length) return -1;//越界了
// 需要翻转
// diff[i]++; // diff[i]之后不会用到,所以注释掉
revCnt++; //由diff[i]++引起,
diff[i + k]--;
count++;
}
}
return count;
}
}