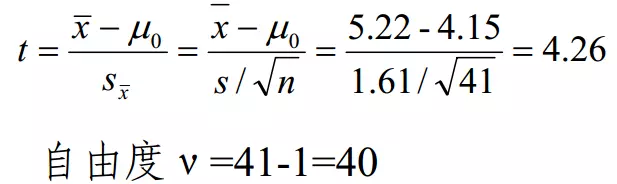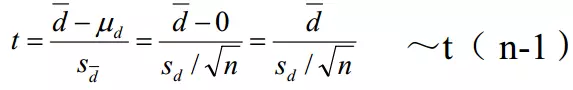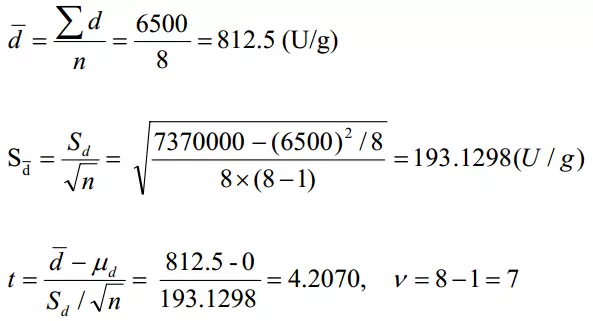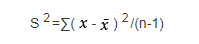显著性检验简介

假设检验也叫显著性检验，是以小概率反证法的逻辑推理，判断假设是否成立的统计方法，它首先假设样本对应的总体参数（或分布）与某个已知总体参数（或分布）相同，然后根据统计量的分布规律来分析样本数据，利用样本信息判断是否支持这种假设，并对检验假设做出取舍抉择，做出的结论是概率性的，不是绝对的肯定或否定。

检验假设是针对总体特征而言，包括相互对立的两个方面，即两种假设：一种是无效假设或称原假设、零假设，符号为H0，它是要否定的假设；另一种是备择假设，记为H1，它是H0的对立面。二者是从反证法的思想提出的， H1和H0是相互联系、又相互对立的假设。

假设检验还需根据不同研究目的事先设置是否拒绝原假设的判断标准，即检验水准。检验水准也称显著性水准，它指无效假设H0为真，但被错误地拒绝的一个小概率值，一般取检验水准α =0.05。

t检验

单侧检验与双侧检验（区别在于是否知道标准）

• 在进行t检验时，如果其目的在于检验两个总体均数是否相等，即为双侧检验。 例如检验某种新降压药与常用降压药效力是否相同？就是说，新药效力可能比旧药好，也可能比旧药差，或者力相同，都有可能。
• 如果我们已知新药效力不可能低于旧药效力，例如磺胺药+磺胺增效剂从理论上推知其效果不可能低于单用磺胺药，这时，无效假设为H0：μ1=μ2, 备择假设为H1： μ1>μ2 , 统计上称为单侧检验。

单侧和双侧的区分在于是否知道标准，后面的栗子可以体会得到。

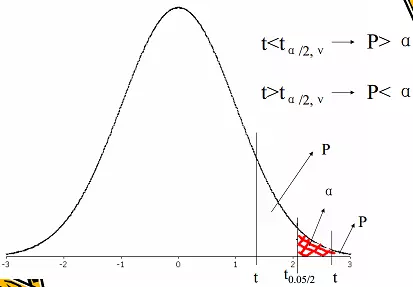
确定P值和做出推断结论

这里的P值是指由H0成立时的检验统计量出现在由样本计算出来的检验统计量的末端或更末端处的概率值。
当P≤ α时，结论为按所取检验水准拒绝H0，接受H1，这样做出结论的理由是：在H0成立的条件下，出现等于及大于现有检验统计量值的概率P≤ α ，是小概率事件，这在一次抽样中是不大可能发生的，即现有样本信息不支持H0因而拒绝它；若P>α，即样本信息支持H0，就没有理由拒绝它，此时只好接受它。

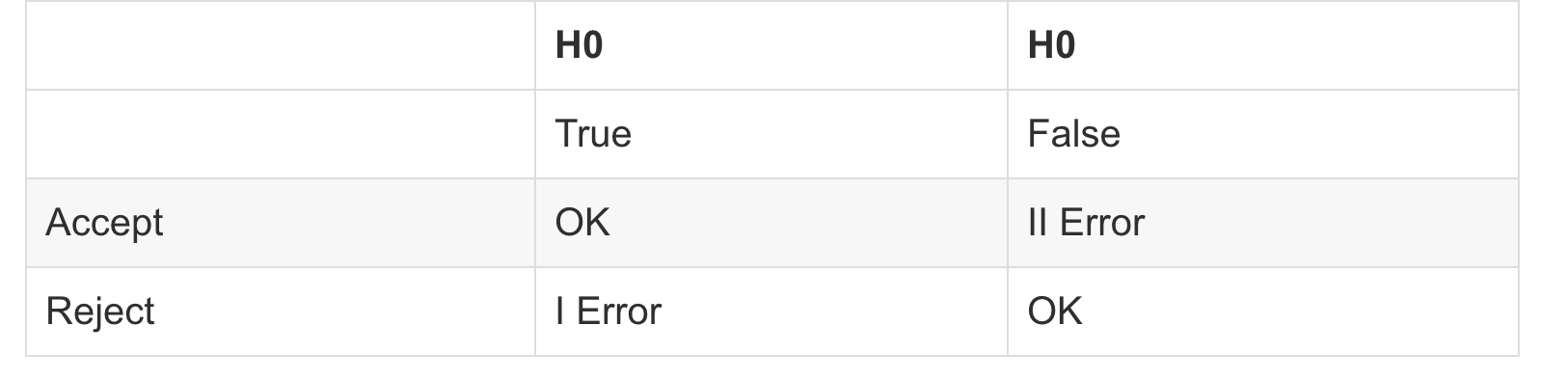
假设检验的两类错误
Ⅰ型错误，第一类错误、假阳性错误,就是在假设检验作推断结论时，拒绝了实际上是正确的原假设H0，其概率用α表示。（拒绝正确）
Ⅰ型错误是针对原假设而言的， α就是事先规定 的 允 许 犯 Ⅰ 型 错 误 的 概 率 值 ， 如 规 定α=0.05，意味着在某特定总体抽样， 100次拒绝H0的假设检验中，最多有5次允许发生第一类错误。与此相应，推断正确的可能性为1-α， 1-α又称为可信度。
Ⅱ型错误，第二类错误、假阴性错误， 即接受实际上是不成立的H0。就是无效假设原本是不正确的，但所算得的统计量不足以拒绝它，错误地得出了无差别的结论。（接受错误）
Ⅱ型错误是针对备择假设而言的，其概率值用β表示。β值的大小一般未知，只有在不
同总体特征已知的基础上，按预定的α和n才能做出估算。

T检验例子

栗子no.1

大量检测已知正常人血浆载脂蛋白E（ apo E）总体平均水平为4.15mmol/L。某医师经抽样测得41例陈旧性心机梗死患者的血浆载脂蛋白E平均浓度为5.22mmol/L，标准差为1.61mmol/L。据此能否认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的平均浓度不一致？
（1）建立检验假设和确定检验水准。H0: μ=μ0，H1: μ≠μ0，α=0.05，双侧检验；
（2）选定检验方法和计算统计量。用单样本的t检验，单侧检验的公式如下图所示：

（3） 确定P值和作出推断结论。查t分布表(正态分布表)， t0.05/2,40=2.021， t=4.26>t0.05/2,40，P<0.05。按α=0.05水准，拒绝H0，接受H1，可认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的差别有统计学意义，结合专业可以认为前者平均浓度较高。

栗子No.2

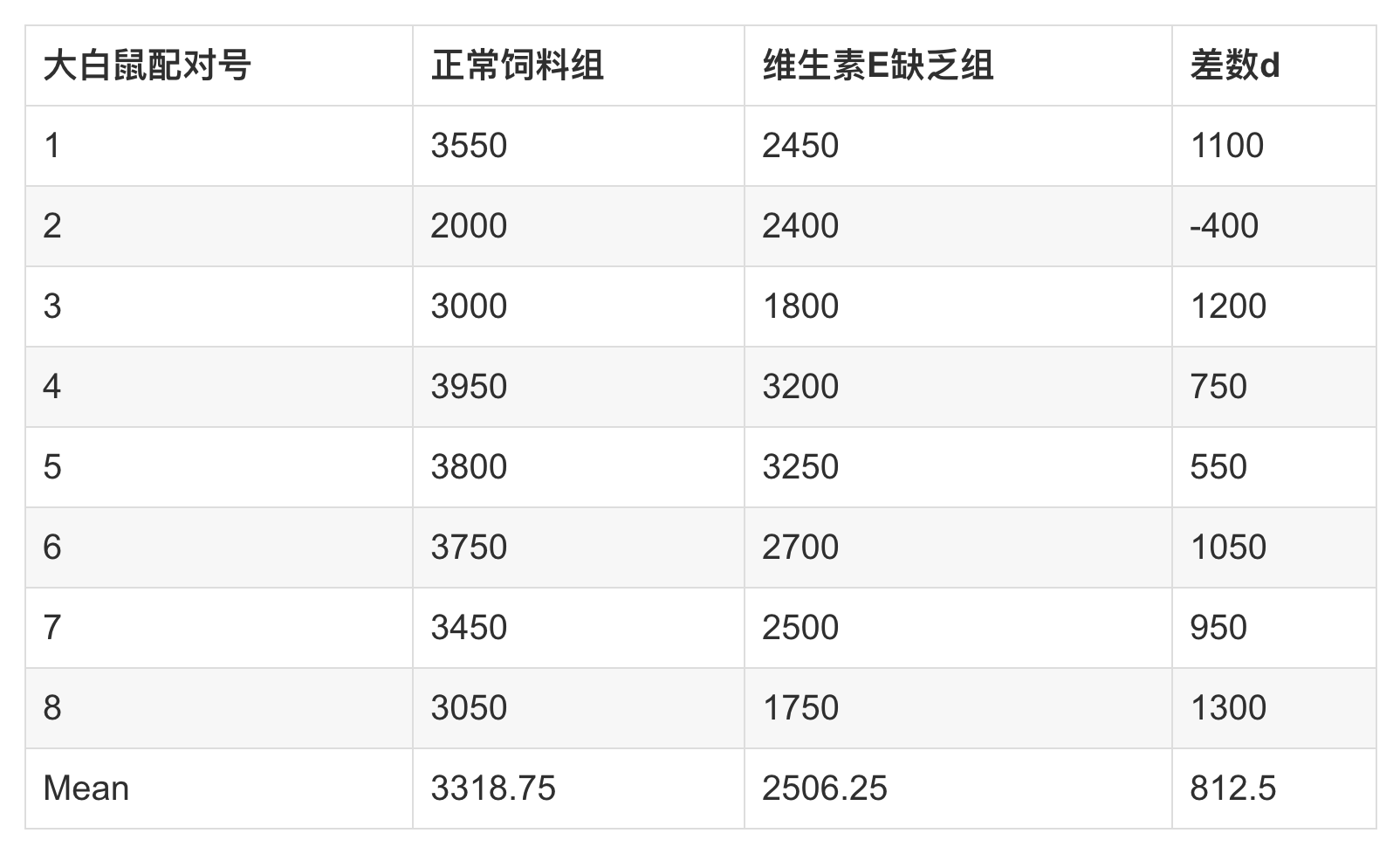
将大白鼠配成8对，每对分别饲以正常饲料和缺乏维生素E饲料，测得两组大白鼠肝中维生素A的含量，试比较两组大白鼠中维生素A的含量有无差别。

（1）建立检验假设和确定检验水准。H0: μd=0，H1: μd≠0，α=0.05，双侧检验；
（2）选定检验方法和计算统计量。
首先计算出各对差值d的均数。当两种处理结果无差别或某种处理不起作用时，理论上差值d的总体均数μd=0。
可将配对设计资料的假设检验视为样本均数与总体均数μd=0的比较。
双侧检验的公式如下：


（3） 确定P值和作出推断结论。查t分布表（双侧）， t=4.2>t 0.05/2, 7 =2.365,P<0.05。按 α＝ 0.05水准，拒绝H0，接受H1,可以认为两种饲料喂养的两组大白鼠中维生素A的含
量有差别。正常饲料组比缺乏维生素Ｅ饲料组的含量要高。

F检验

F检验（F-test），最常用的别名叫做联合假设检验（英语：joint hypotheses test），此外也称方差比率检验、方差齐性检验，方差分析，它是一种在（H0）之下，统计值服从的检验。其通常是用来分析用了超过一个参数的统计模型，以判断该模型中的全部或一部分参数是否适合用来估计总体。
计算
（1）样本标准偏差的平方。

两组数据就能得到两个平方值$S^2$和$S^{\prime 2}$。

（2）$F=S^2/S^{\prime 2}$

（3）然后计算的F值与查表得到的F表值比较，如果
F < F表 表明两组数据没有显著差异；
F ≥ F表 表明两组数据存在显著差异。