One PUNCH Man——聚类

文章目录

聚类介绍
- 性能度量
- 距离计算
k-means
学习向量量化
高斯混合聚类
DBSCAN密度聚类
层次聚类

聚类介绍

在"无监督学习" (unsupervised learning) 中，训练样本的标记信息是未知的。目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。此类学习任务中研究最多、应用最广的是"聚类" (clustering).

性能度量

暂不介绍，概念太多，比较简单。和变量显著性检验有写类似。

距离计算

给定样本 $x=(x_1,x_2,...,x_n)$ 和样本 $y=(y_1,y_2,...,y_n)$ ，最常用的闵可夫斯基距离公式如下：
$dist_{mk}(x,y)=(\sum_{i=1}^{n}|x_i-y_i|^p)^{\frac{1}{p}}$

当 $p = 2$ 时，该公式变成欧式距离：

$dist_{ed}(x,y)=\sqrt{\sum_{i=1}^{n}|x_i-y_i|^2}$

当 $p = 1$ 时，该公式又变成曼哈顿距离：

$dist_{man}(x,y)=\sum_{i=1}^{n}|x_i-y_i|$

我们常将属性划分为"连续属性" (continuous attribute)和"离散属性" (categorical attribute)。一般来说连续属性，是可以通过其属性值计算距离的，比如1距离2比1距离3近。而离散属性，一般很难直观的看出距离，比如{飞机，轮船，火车}，这三者之间的距离就无法在属性值（可能用1，2，3来分别表示）来计算，对无序属性，可以通过VDM来计算，但在这里不做介绍，只提到该概念即可。

k-means

简单说一下k均值算法，很简单。（以下均假设样本是二维的，实际上可能更多维，选取二维样本方便叙述）
输入：
样本集合 $D=\{(x_1,y_1),(x_2,y_2),....,(x_m,y_m)\}$
聚类簇数： $k$ （也就是说样本被分为k个类）
样本距离度量方式
过程：

随机选取 $k$ 个样本点，作为初始质心。
计算未选中的 $m - k$ 个点分别到这 $k$ 个质心的距离，并将其划分到距离最近的簇中。
重新计算 $k$ 个簇的新质心，比如求簇的中点。
重复上述2和3过程，直到质心变化很小或者不变化。
输出 $k$ 个质心。

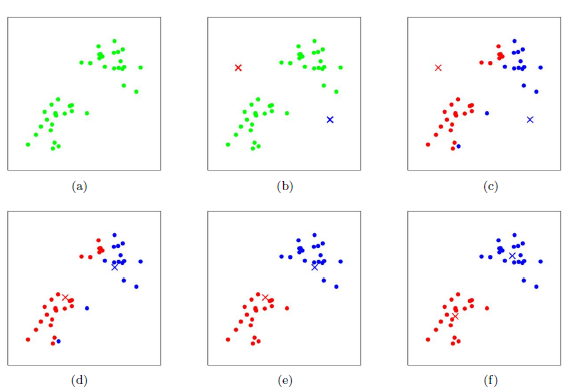
$k = 2$ 的一个划分过程如下图所示：
在这里插入图片描述

学习向量量化

与k 均值算法类似，“学习向量量化”（LVQ）也是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是， LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
输入：
样本集合 $D=\{(x_1,y_1),(x_2,y_2),....,(x_m,y_m)\}$
原型向量个数 $q$ ，各原型向量预设的类别标记： ${t_1,t_2,...,t_q\}$
学习率 $\eta$
样本距离度量方式
过程：

初始化 $q$ 个原型向量 ${p_1,p_2,...,p_q\}$
计算样本点 $x_i,y_i)$ 到 $q$ 个原型向量 $p_j$ 的距离，取距离最近的原型向量 $p_j$ 并与样本点 $x_i,y_i)$ 做出以下判断：
$i f :$ $y_i=t_j$ //这里 $t_j$ 是 $p_j$ 对应的原型向量类别标记
$t h e n :$ $p_j=p_j+\eta (x_i-p_j)$
$e l s e :$ $p_j=p_j-\eta (x_i-p_j)$
重复上述步骤，直到满足停止条件。
输出 $q$ 个原型向量 ${p_1,p_2,...,p_q\}$

高斯混合聚类

高斯混合聚类采用概率模型来表达聚类原型。有兴趣可以了解以下，在此不做赘述。

DBSCAN密度聚类

DBSCAN是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。
通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。
DBSCAN是基于一组邻域来描述样本集的紧密程度的，参数 $(\epsilon, MinPts)$ 用来描述邻域的样本分布紧密程度。其中，ϵ描述了某一样本的邻域距离阈值，MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。
假设我的样本集是 $D=\{(x_1,y_1),(x_2,y_2),....,(x_m,y_m)\}$ ,则DBSCAN具体的密度描述定义如下：

$\epsilon$ -邻域：对于任意样本 $x_i,y_i)$ ，其 $\epsilon$ -邻域包含样本集D中与 $x_i,y_i)$ 的距离不大于 $\epsilon$ 的子样本集，即存在一个区别于 $x_i,y_i)$ 的样本点 $x_j,y_j)$ ，使得他们之间的距离小于 $\epsilon$ ，记为： $N_{\epsilon}((x_j,y_j))=\{x_i∈D|distance ((x_i,y_i),(x_j,y_j))≤ \epsilon\}$ ，其满足该条件的样本个数为 $N_{\epsilon}((x_j,y_j))$
核心对象：对于任一样本 $x_j,y_j)∈D$ ，如果其ϵ-邻域对应的 $N_{\epsilon}((x_j,y_j))$ 至少包含 $M i n P t s$ 个样本，即如果 $|N_{\epsilon}((x_j,y_j))|≥MinPts$ ，则 $x_j,y_j)$ 是核心对象。
密度直达：如果 $x_j,y_j)$ 位于 $x_i,y_i)$ 的ϵ-邻域中，且 $x_i,y_i)$ 是核心对象，则称 $x_j,y_j)$ 由 $x_i,y_i)$ 密度直达。注意反之不一定成立，除非且 $x_j,y_j)$ 也是核心对象。
密度可达：如果 $x_j,y_j)$ 位于 $x_i,y_i)$ 的ϵ-邻域中，如果 $x_k,y_k)$ 位于 $x_j,y_j)$ 的ϵ-邻域中，且个样本点 $x_j,y_j)$ 和 $x_i,y_i)$ 都是核心对象（最后一个样本点不用是核心对象），则称 $x_k,y_k)$ 对 $x_i,y_i)$ 密度可达。同样密度可达也不是对称的，反之可能不成立。
密度相连，如果 $x_j,y_j)$ 对于 $x_i,y_i)$ 密度可达，如果 $x_k,y_k)$ 对于 $x_i,y_i)$ 密度可达，且 $x_i,y_i)$ 是核心对象，则称 $x_j,y_j)$ 和 $x_k,y_k)$ 密度相连，这可以是对称的。

在这里插入图片描述
DBSCAN的聚类定义很简单：由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。

输入：
样本集合 $D=\{(x_1,y_1),(x_2,y_2),....,(x_m,y_m)\}$
邻域参数 $(\epsilon,MinPts)$
样本距离度量方式
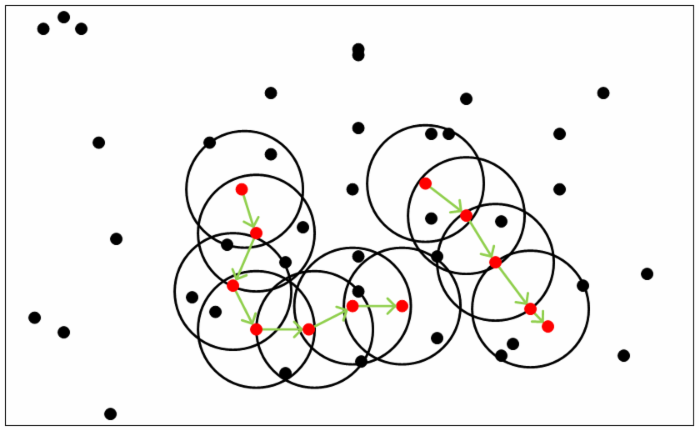
过程：

对于每一个样本点，找到其所有的核心对象，把所有核心对象的集合称为 $\Omega$ 。
随机选取 $\Omega$ 里的一个核心对象 $x_i,y_i)$ ，加入到簇 $C_i$ 中。
找到簇 $C_i$ 未使用过的核心对象，找到其领域内的其他样本 $x_j,y_j)$ ，如果有样本是核心样本，则把 $\Omega$ 里的该样本去掉 $x_j,y_j)$ 。把样本 $x_j,y_j)$ 加入到该簇 $C_i$ 中。
重复步骤3直到簇 $C_i$ 里没有未使用过的核心对象。
重复步骤234，直到核心对象集合为空。
输出得到的簇 ${C_1,C_2,....\}$ （未包括在簇里的点就是噪声点）

在这里插入图片描述

层次聚类

AGNES 是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个粟类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。这里的关键是如何计算聚类簇之间的距离。每个簇是一个样本集合，因此，只需采用关于集合的某种距离即可。
下面介绍一下豪斯多夫距离：

最小距离：取两个簇最近的两个向量计算其距离。
最大距离：取两个簇最远的两个向量计算其距离。
平均距离：取两个簇所有向量之间的距离，计算其平均值。

输入：
假设样本集合 $D=\{x_1,x_2,....,x_m\}$ ，其中 $x$ 都是向量表示。
聚类簇数 $k$ 。
距离度量函数。
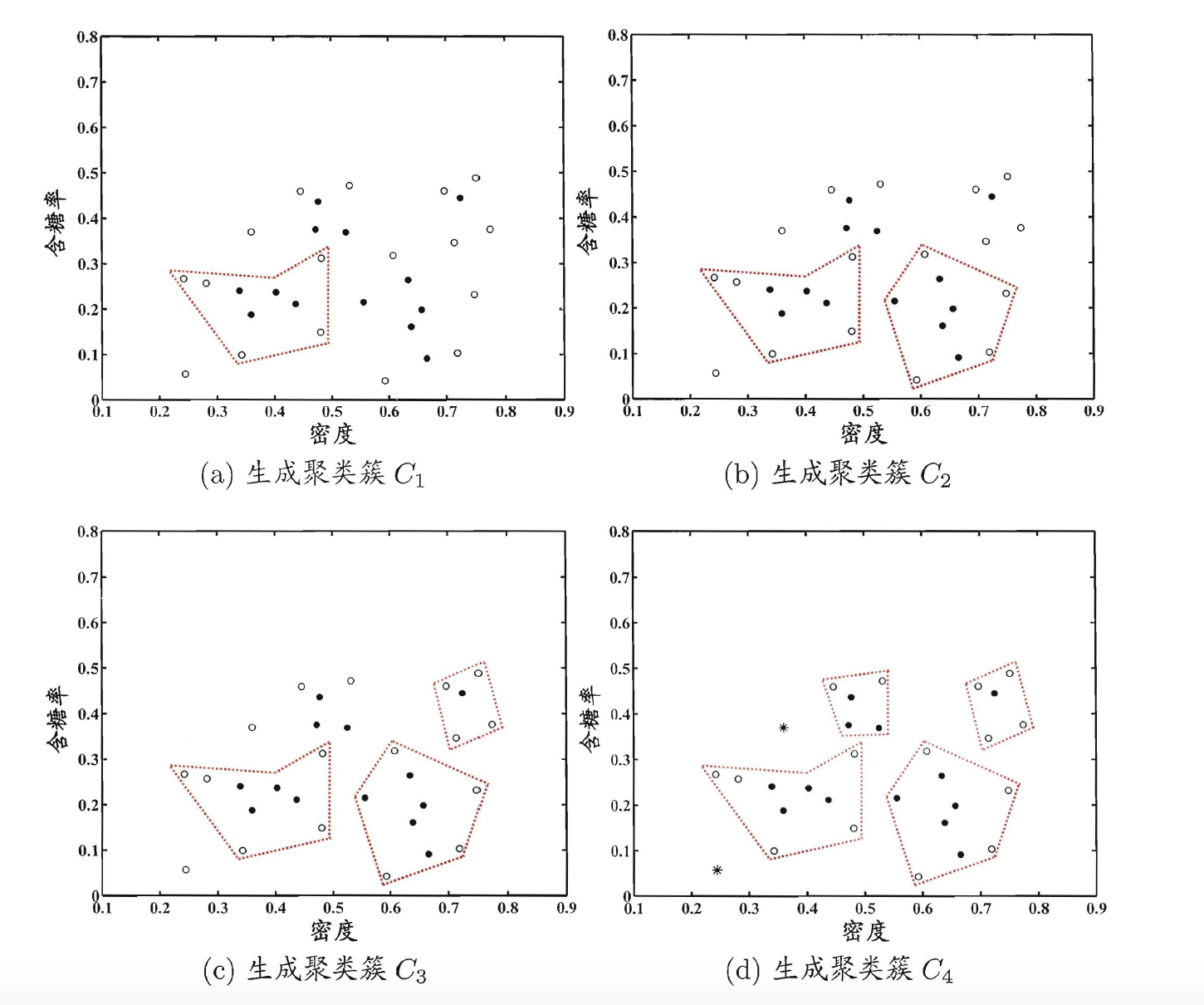
过程：

把每个样本定义为一个簇，最终有m个簇。
计算每个簇之间的距离，找出距离最短的那两个簇，合并为一个簇。
重复上述步骤2的过程，直到簇的数量为k。

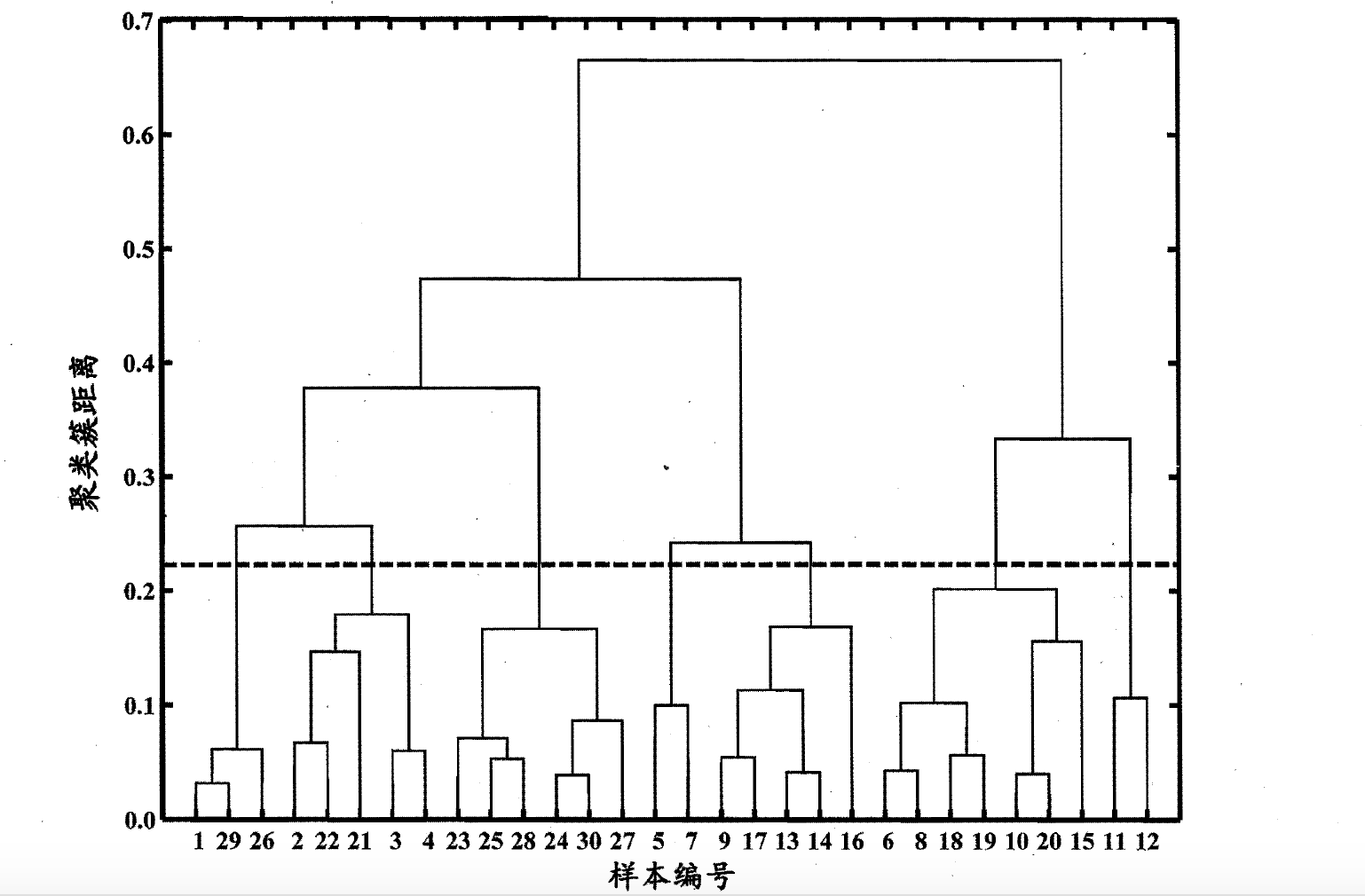
如果k=1，计算步骤如下图所示：
在这里插入图片描述