本章记录一些有关二叉树的一些较为经典或者自己第一次做印象比较深刻的算法以及题型,包含自己作为初学者第一次碰到题目时想到的思路以及网上其他更优秀的思路,本章持续更新中......
目录
一、二叉树遍历
No 144. 二叉树的前序遍历(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
题目描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
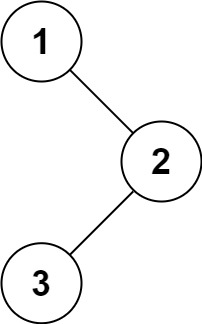
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]思路:通过这个题对递归遍历的前、中、后序遍历和迭代遍历的前序、后序遍历方式做一个总结。为什么这里不总结迭代方式的中序遍历呢?因为迭代法的中序遍历和前序、后序的代码逻辑有所不同。
递归法:使用递归的三个最重要的部分就是1、确定递归函数的参数和返回值;2、确认递归函数的终止条件;3、确认递归函数的逻辑。
1、确定递归函数的参数和返回值:由于题目要求返回节点值,所以要用一个容器来保存节点值,同时还要有一个节点参数。
2、确定递归函数的终止条件:如果当前拿到的节点为NULL,则递归结束
3、确定递归函数的逻辑:前序遍历的顺序是中左右,所以要先处理中加节点的值,然后再递归处理左右节点。如果是中序和后序,只需要调换代码顺序即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归法
void doPreorderTraversal(TreeNode* cur,vector<int>& res){
if(cur==NULL){
return;
}
//前序遍历:中左右,其他顺序只需要调换代码位置即可
res.push_back(cur->val);
doPreorderTraversal(cur->left,res);
doPreorderTraversal(cur->right,res);
}
//递归法
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
doPreorderTraversal(root,res);
return res;
}
};迭代法:迭代法相比于递归法要复杂一点,需要用一个栈来实现。利用栈的后进先出特点,先把跟节点入栈,然后只要栈不为空就进入循环,在循环中,拿到栈顶节点并出栈,然后将栈顶节点的值放到结果中,之后先将右节点入栈,再将左节点入栈。因为栈是后进先出,所以要先把右节点入栈,这样出栈的时候右节点就是后入栈的,这是前序遍历的思路。对于后序遍历,要实现左右中的遍历顺序,其实可以把前序遍历稍加修改,编程中右左的顺序遍历,最后再把结果翻转一下,不就是左右中的遍历顺序了。后序遍历的迭代和前序遍历的迭代代码风格和逻辑上有很大的相似之处,主要原因是要处理的节点就是每次拿到的节点,都是中间节点。中序则不同,要处理的节点和拿到的节点不是同一个,所以递归的逻辑有所不同。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//迭代法
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> treeStack;
vector<int> res;
if(root==NULL){
return res;
}
//先把树根入栈
treeStack.push(root);
while(!treeStack.empty()){
//遍历栈中的节点,拿到以后就出栈
TreeNode* cur=treeStack.top();
treeStack.pop();
//把这个节点的数值放入结果中
res.push_back(cur->val);
//先把右节点入栈,才能保证出栈的时候先拿到左节点
if(cur->right!=NULL){
treeStack.push(cur->right);
}
if(cur->left!=NULL){
treeStack.push(cur->left);
}
}
return res;
}
};No 94. 二叉树的中序遍历(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
题目描述:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
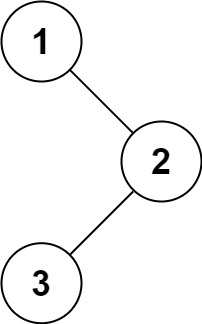
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]思路:利用这一题来总结一下中序遍历的迭代法和统一风格的前中后序遍历的迭代方式代码。
中序遍历迭代法:中序遍历的迭代法需要特殊处理一下,因为要处理的节点和每次拿到的节点不一样。所以如果拿到的节点不为NULL,那么就把该节点入栈,然后移动到该节点的左节点(注意是移动,不是入栈),进行下一轮循环。如果当前拿到的节点为NULL,表示此时栈顶的节点就是这课二叉树最左下方的节点了,此时拿到该节点并出栈,然后把该节点的值添加到结果中,最后移动到该节点的右节点,之后开始下一轮循环。文字描述可能有点难理解,最好可以画个图感受下,可以加深理解。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
// //递归法
// vector<int> res;
// doInorderTraversal(root,res);
// return res;
//迭代法
stack<TreeNode*> treeStack;
vector<int> res;
TreeNode* cur=root;
while(!treeStack.empty()||cur!=NULL){
//有左节点
if(cur!=NULL){
treeStack.push(cur);
cur=cur->left;
}
//没有左节点了
else{
//此时栈顶是没有左节点的那个节点,也就是当前的中间节点
cur=treeStack.top();
//一般是拿到就出栈,防止遗漏
treeStack.pop();
//把中间这个节点添加到结果中
res.push_back(cur->val);
//访问这个节点的右节点
cur=cur->right;
}
}
return res;
}
};统一风格的三种遍历方式的迭代法:一般的迭代法在在三种遍历方式中代码风格不统一,因此如果有一种统一的代码风格和相似的逻辑,只需要想递归那样变换代码顺序就会方便不少。要想做到这一点,就需要对中间节点进行一个特殊处理,先进行记录,最后在进行统一的处理。我们可以在每次中间节点入栈后在入栈一个NULL,后续只有当遍历到NULL的时候,再处理节点的值。具体方法是,在进入循环之前先把根节点入栈,循环结束条件是栈为空。在循环中,从栈顶拿到一个节点并弹出,只要当前节点不为空,我们就入栈,入栈的具体方式要看是什么遍历方式,以中序遍历为例,先入栈右节点,再入栈中间节点,最后入栈左节点,注意要在中间节点入栈之后紧跟一个NULL。如果当前拿到的节点是NULL,那么此时栈顶元素就是要处理的中间节点(因为在循环开始时,拿到栈顶的NULL后就弹出了)。此时只需要拿到栈顶节点并弹出,对节点的值进行记录即可。这样就做到了代码的风格统一,对于不同的遍历顺序,只需要改变入栈的代码顺序即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//统一写法:左中右
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> treeStack;
//root不为空,先入栈
if(root!=NULL){
treeStack.push(root);
}
//开始遍历,左中右的时候要先入栈右节点,其他遍历方式调换顺序即可
while(!treeStack.empty()){
//拿到第一个节点就出栈,防止重复
TreeNode* cur=treeStack.top();
treeStack.pop();
//遇到非空节点都要判断左中右节点并执行对应入栈逻辑
if(cur!=NULL){
//右节点入栈
if(cur->right!=NULL){
treeStack.push(cur->right);
}
//中间节点,加入一个NULL,表示这是待处理的节点
treeStack.push(cur);
treeStack.push(NULL);
//左节点入栈
if(cur->left!=NULL){
treeStack.push(cur->left);
}
}
//遇到了空节点,表示下一个节点是要处理的节点
else{
//拿到栈顶元素,此时已经不是NULL了,是要处理的节点
cur=treeStack.top();
treeStack.pop();
//把value放入结果中
res.push_back(cur->val);
}
}
return res;
}
};No 102. 二叉树的层序遍历 (中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
题目描述:
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
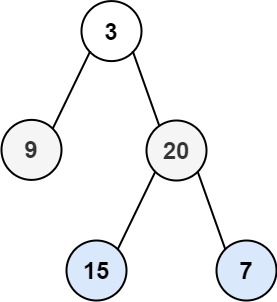
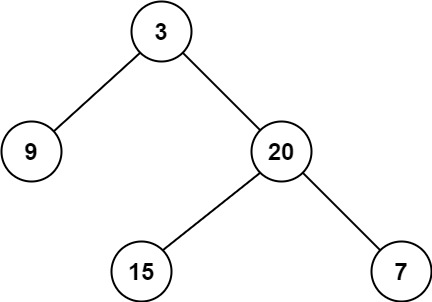
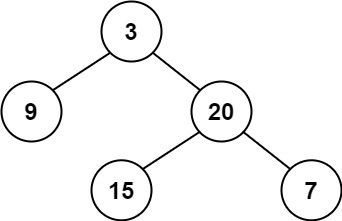
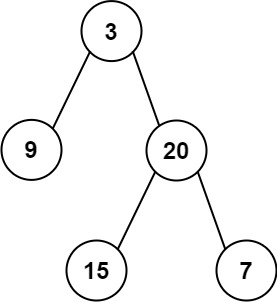
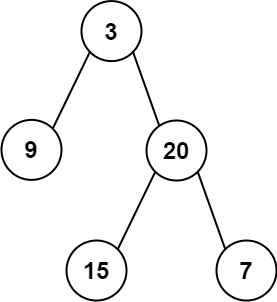
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]思路:这一题来总结一下层级遍历,也就是广度优先搜索。层先遍历就是按照一层一层的顺序来遍历,结合示例应该可以很容易理解。要做到层先遍历,一个关键点是要拿到每一层的节点数量,这个节点数量可以通过队列的大小来获取。层先遍历需要使用到队列,而不是栈。队列先进先出的特点可以很好的把节点的顺序记录下来。具体方法是:首先将根节点入队,然后进入循环,循环的结束条件是队列为空。在循环中,我们要做的是首先是得到此时队列的大小,因为每一轮循环开始之前的队列的大小就是当前层的节点数量。拿到节点数量之后我们就可以在一个 for 循环中对这一层的节点进行操作了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> treeQueue;
vector<vector<int>> res;
if(root!=NULL){
treeQueue.push(root);
}
while(!treeQueue.empty()){
vector<int> res_eachLine;
//每一层的大小,因为返回的是二维的vector,所以要在循环内定义一个一维的vector存档当前层的结果
int lineSize=treeQueue.size();
for(int i=0;i<lineSize;i++){
TreeNode* cur=treeQueue.front();
treeQueue.pop();
res_eachLine.push_back(cur->val);
if(cur->left!=NULL){
treeQueue.push(cur->left);
}
if(cur->right!=NULL){
treeQueue.push(cur->right);
}
}
res.push_back(res_eachLine);
}
return res;
}
};No 429. N 叉树的层序遍历(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/n-ary-tree-level-order-traversal/
题目描述:
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]示例 2:
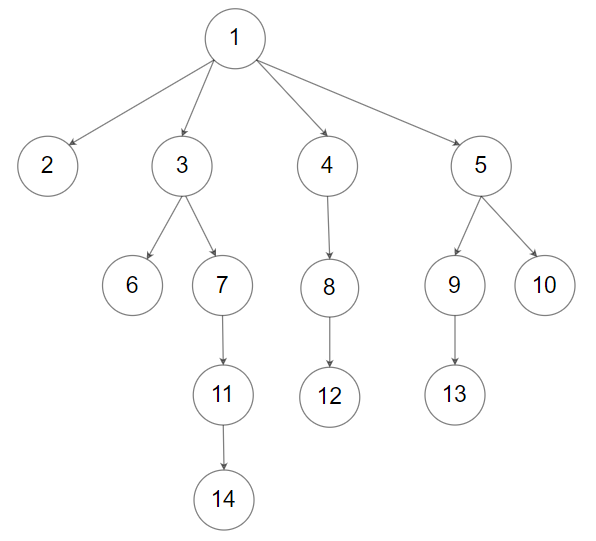
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]思路:本题其实是层先遍历的扩展,把子节点从2个扩展成为了n个。做法和思路是一样的,唯一不同的地方在于对入栈的处理。二叉树中子节点是两个,我们可以用两行代码来入队,N叉树其实也是一样的道理,只不过入栈的时候需要用 x 行代码来入队,这个 x 就是当前节点的子节点数量。所以相比于二叉树,我们要再多获取一个值,就是当前节点的子节点数量,根据代注释中给出的定义,我们知道子节点是用vector保存的,可以用一个size()来获取数量,之后用for循环入栈即可。
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
queue<Node*> treeQueue;
if(root!=NULL){
treeQueue.push(root);
}
//层先遍历
while(!treeQueue.empty()){
//获取层的大小
int lineSize=treeQueue.size();
//用于存放每一层的数据
vector<int> lineTemp;
//每一层遍历
for(int i=0;i<lineSize;i++){
//拿到第一个节点然后弹出
Node* cur=treeQueue.front();
treeQueue.pop();
//把第一个节点的val写入结果
lineTemp.push_back(cur->val);
//获取孩子数量,把所有的孩子节点加入队列,cur->children是一个vector
int childrenNum=cur->children.size();
//把不为空的孩子节点加入队列
for(int j=0;j<childrenNum;j++){
if(cur->children[j]!=NULL){
treeQueue.push(cur->children[j]);
}
}
}
//把每一层的写入到结果队列中
res.push_back(lineTemp);
}
return res;
}
};二、二叉树的属性
No 101. 对称二叉树(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/symmetric-tree/
题目描述:
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
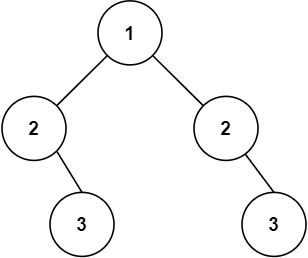
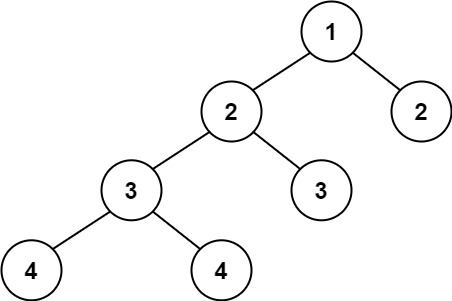
输入:root = [1,2,2,3,4,4,3]
输出:true示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false思路:这个题其实就是判断左右子树是否反向相等,所谓反向相等,就是看左子树的左子树和右子树的右子树、左子树的右子树和右子树的左子树是否相等。通过这句话的描述也可以感受到,用递归做这个会比较好一些。还是递归的三要素,参数返回值+递归终止条件+递归逻辑。
参数和返回值:由于不需要记录节点值之类的所以参数就传入节点就好;
终止条件有这样几种情况:1、左节点已经是NULL了,右节点还不是NULL或者反过来。2、左右同时为空,此时说明这两个子树是相等的。3、两个节点的值不同,则不是相同的树。4、如果上述都不符合,那说明当前来看是相同的子树。注意以上说明的都是如何判断两个树是否相同,要想判断是不是对称的,那就要在递归参数上做文章。前面说到,判断对称就是判断是否反向相等,如果当前节点满足终止条件4,那就应该继续判断后面的节点,也就是判断子树是否对称,也就意味着要递归调用,调用递归的时候这样调用:外侧和外侧比较,内侧和内侧比较,这样就可以判断是否对称。
compare(node1->left , node2->right) && compare(node1->right , node2->left);
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//迭代法
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> treeStack;
vector<int> res;
if(root==NULL){
return res;
}
//先把树根入栈
treeStack.push(root);
while(!treeStack.empty()){
//遍历栈中的节点,拿到以后就出栈
TreeNode* cur=treeStack.top();
treeStack.pop();
//把这个节点的数值放入结果中
res.push_back(cur->val);
//先把右节点入栈,才能保证出栈的时候先拿到左节点
if(cur->right!=NULL){
treeStack.push(cur->right);
}
if(cur->left!=NULL){
treeStack.push(cur->left);
}
}
return res;
}
};No 111. 二叉树的最小深度(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
题目描述:
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明:叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:2示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5思路:这个题其实就是找叶子结点也就是没有孩子节点的节点。这个题有两种做法,一种是广度优先,层级遍历,一层一层的遍历,遇到的第一个没有孩子节点的节点就是叶子结点,此时的层数就是最小深度。第二种就是递归,递归的参数是节点,返回值是当前左右子树的最小深度+根节点的深度1;递归终止条件是当前节点没有左右子节点,注意如果左子树为空但是右子树不为空,此时的最小深度是右子树的最小深度+1,反之亦然;递归逻辑则是每次都把左节点和右节点作为参数进行递归调用。
还有一个找最大深度的题,其实也是一样的。可以用层级遍历,遍历完以后得到的层数就是最大深度。也可以使用后序遍历,避免回溯,得到根节点的高度,高度的数值和深度的数值是一样的。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//最低深度就是第一个没有孩子节点的的节点
int minDepth(TreeNode* root) {
queue<TreeNode*> treeQueue;
if(root!=NULL){
treeQueue.push(root);
}else{
return 0;
}
//开始遍历
int depth=0;
while(!treeQueue.empty()){
//记录深度
depth++;
int lineSize=treeQueue.size();
//层级遍历
for(int i=0;i<lineSize;i++){
//记住一般情况都是拿到值就弹出
TreeNode* cur=treeQueue.front();
treeQueue.pop();
//当一个节点没有左孩子也没有右孩子的时候,这就是叶子结点
//第一个遍历到的叶子结点就是最浅深度
if(cur->left==NULL&&cur->right==NULL){
return depth;
}
//正常入队
if(cur->left!=NULL){
treeQueue.push(cur->left);
}
if(cur->right!=NULL){
treeQueue.push(cur->right);
}
}
}
return depth;
}
// //递归法
// int getDepth(TreeNode* node){
// if(node==NULL){
// return 0;
// }
// int leftTreeDepth=getDepth(node->left);
// int rightTreeDepth=getDepth(node->right);
// //此时不是最低点,因为右子树不是空
// if(node->left==NULL&&node->right!=NULL){
// return 1+rightTreeDepth;
// }
// //此时不是最低点,因为左子树不是空
// if(node->left!=NULL&&node->right==NULL){
// return 1+leftTreeDepth;
// }
// int depth=1+min(leftTreeDepth,rightTreeDepth);
// return depth;
// }
// int minDepth(TreeNode* root) {
// return getDepth(root);
// }
};No 110. 平衡二叉树(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/balanced-binary-tree/
题目描述:
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:true示例 2:
输入:root = [3,9,20,null,null,15,7]
输出:true示例 3:
输入:root = []
输出:true思路:这个题的思路是利用递归来拿到左右子树的深度,如果深度差值大于1那么就不是平衡二叉树,否则就继续递归调用,看左右子树是否是平衡二叉树。如果遍历到节点为空,那么这就是一个平衡二叉树。思路是比较简单的,但是在实现的时候我有点写的复杂了,不仅递归调用了得到深度的函数,还递归调用了判断是否是平平衡二叉树的函数,相当于递归中又调用了递归。可以进行优化,在拿到深度的递归函数中,如果当前子树深度的差值大于1了,那就返回-1 ,否则继续调用。如果递归拿到的深度是-1,那就直接返回-1。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//获取左子树和右子树的最大深度
int getDepth(TreeNode* node){
if(node==NULL){
return 0;
}
int leftTreeDepth=getDepth(node->left);
int rightTreeDepth=getDepth(node->right);
int depth=1+max(leftTreeDepth,rightTreeDepth);
return depth;
}
//判断是否是平衡二叉树
bool isBalanced(TreeNode* root) {
if(root==NULL){
return true;
}
//判断左子树和右子树的最大深度差值是否大于1
if(fabs(getDepth(root->left)-getDepth(root->right))>1){
return false;
}
//当前左右子树深度差值小于1,则继续判断左右子树是否符合
else{
return isBalanced(root->left)&&isBalanced(root->right);
}
}
// //优化:精简主函数的代码,把判断添加在递归函数中,用-1表示不是平衡二叉树
// int getDepth(TreeNode* node){
// if(node==NULL){
// return 0;
// }
// int leftTreeDepth=getDepth(node->left);
// if(leftTreeDepth==-1){
// return -1;
// }
// int rightTreeDepth=getDepth(node->right);
// if(rightTreeDepth==-1){
// return -1;
// }
// //绝对值小于1返回深度,否则反返回-1
// return abs(leftTreeDepth-rightTreeDepth)<1?1+max(leftTreeDepth,rightTreeDepth):-1;
// }
// bool isBalanced(TreeNode* root) {
// return getDepth(root)== -1?false:true;
// }
};No 222.完全二叉树的节点个数(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-complete-tree-nodes/
题目描述:
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
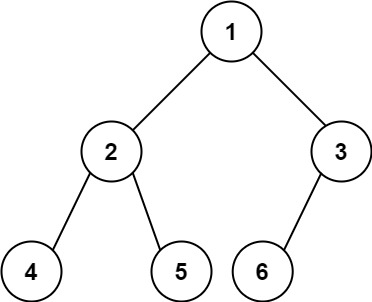
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1思路:这个题最直接的方法就是层级遍历,把每一层的节点数量统计出来,最后遍历完得到的就是节点数。但是这样做的时间负责度是O(n),还可以进行优化。
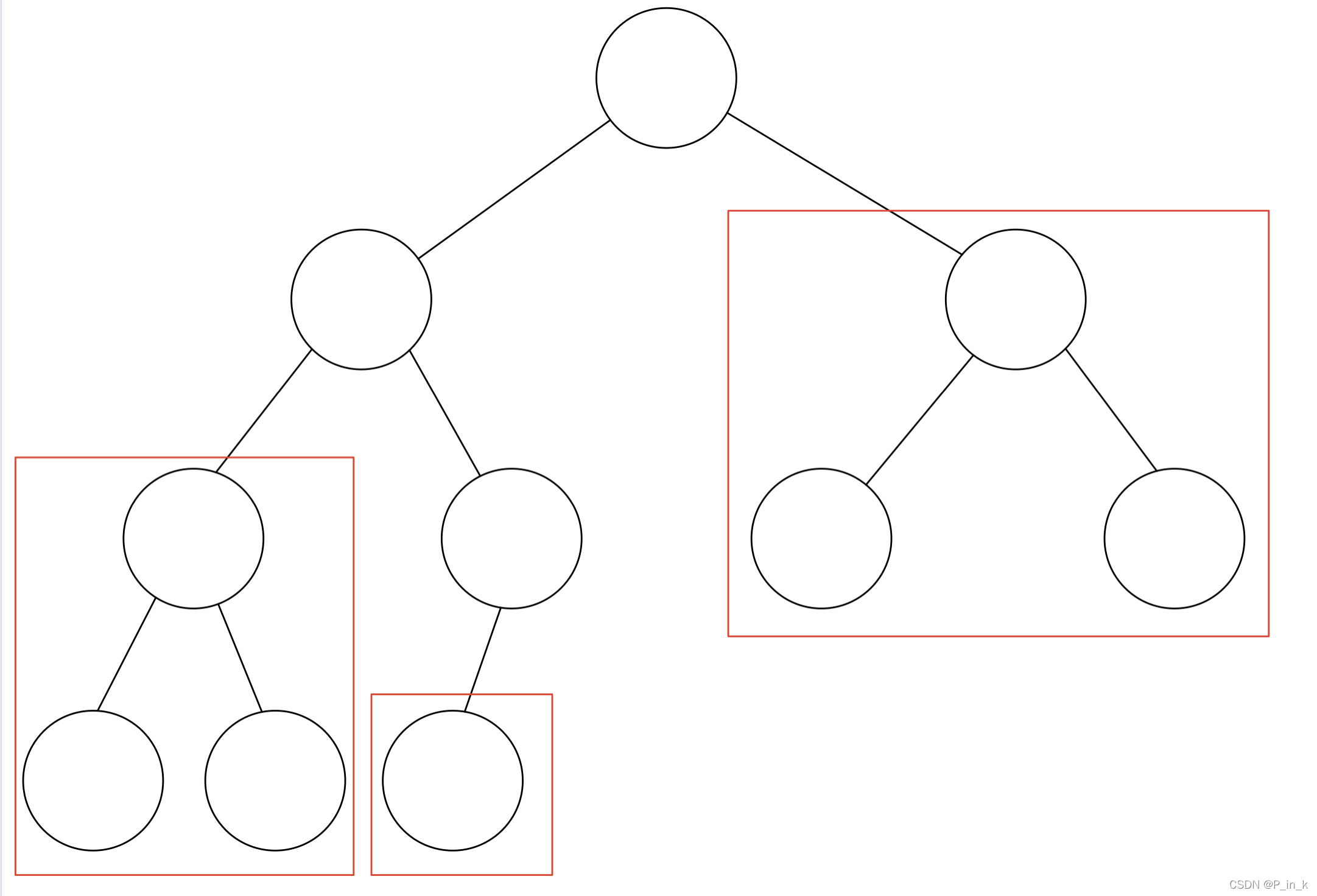
题目中给了完全二叉树这个条件,完全二叉树的特性就是除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。所以根据这个特点,一个完全二叉树一定可以划分为若干个满二叉树,哪怕只有一个节点,也可以是一个满二叉树。最后一层可能无法构成满二叉树,但是通过递归最终一定会有满二叉树。
这样的话,若果是满二叉树,那么直接使用 2^(满二叉树深度) -1 来计算当前层的节点数然后返回即可。如果不是满二叉树,那么就递归左右子树,递归的返回值是左右子树的数量加上根节点,直到遇到满二叉树。其实有一点不好理解,可以跟着下面的代码来一步一步的画图感受一下。如何判断一棵树是不是满二叉树?如果这个树的最左侧深度和最右侧深度相同,那么就是满二叉树,题目已经给了这是完全二叉树的条件,才能这样判断。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//优化方法:一个完全二叉树总是可以分解为N个满二叉树,递归寻找每一个,满二叉子树
int countNodes(TreeNode* root) {
if(root==NULL){
return 0;
}
int leftTreeDepth=0;
int rightTreeDepth=0;
TreeNode* left=root->left;
TreeNode* right=root->right;
//两个循环拿到最左枝和最右枝的深度
while(left!=NULL){
left=left->left;
leftTreeDepth++;
}
while(right!=NULL){
right=right->right;
rightTreeDepth++;
}
//最左枝和最右枝的深度相同则是满二叉树
if(leftTreeDepth==rightTreeDepth){
//(2<<1) 相当于2^2
return (2<<leftTreeDepth)-1;
}
//最后的1是根节点的值
return countNodes(root->left)+countNodes(root->right)+1;
}
// //层先遍历,记录每层大小即可,O(n)
// int countNodes(TreeNode* root) {
// queue<TreeNode*> treeQueue;
// if(root!=NULL){
// treeQueue.push(root);
// }
// int num=0;
// while(!treeQueue.empty()){
// int levelSize=treeQueue.size();
// num+=levelSize;
// for(int i=0;i<levelSize;i++){
// TreeNode* cur=treeQueue.front();
// treeQueue.pop();
// if(cur->left!=NULL){
// treeQueue.push(cur->left);
// }
// if(cur->right!=NULL){
// treeQueue.push(cur->right);
// }
// }
// }
// return num;
// }
};No 257.二叉树的所有路径(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-paths/
题目描述:
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。
示例 1:
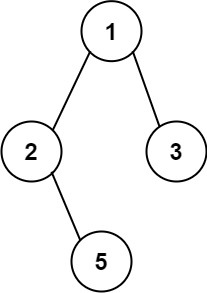
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]思路:这个题说实话第一眼看到感觉不像是简单题,可能是因为第一次接触到需要回溯的问题,而此前还没有接触过回溯。回溯问题一直有着会者不难,难者不会的说法。这个题目的总体思路是利用递归来记录经过的每一个节点的值,当遇到叶子节点的时候,说明这是一条完整的路径。将这个路径构造成字符串写入到结果集中。但是当走到了叶子结点后,怎么回退呢?这里就要用回溯的思想了。其实递归就是回溯的一种表现形式,递归本就是到底后再一层一层返回。如果我们在每次递归调用后再进行一次把路径节点值弹出的操作,那么当递归回退到这里的时候,就把这个已经使用过的节点的值弹出了,就可以实现回溯了。例如本题的代码中,我们对左节点进行递归,每当递归返回到这里时,说明当前这个节点后面所有的路径都已经找完了,当前这个节点的值就没有利用价值了,弹出后对右节点进行递归,也是一样的到道理。
递归的参数和返回值:不需要返回值,直接对路径集和结果集操作即可;参数有节点,路径集和结果集。
递归终止条件:遇到叶子节点,然后利用当前的路径集构造路径字符串,把字符串写入结果集。
递归逻辑:节点不为空就对节点递归调用,递归调用后紧跟一个弹出操作。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归函数:参数有节点、经过的路径的节点值、结果集
void getPath(TreeNode* node,vector<int>& path, vector<string>& res){
//先把当前节点的值记录在路径中
path.push_back(node->val);
//如果到了叶子节点,这是一条路径,如果用node!=作为终止条件就会不好处理,因为不知道这个是不是叶子节点
if(node->left==NULL&&node->right==NULL){
string strPath;
for(int i=0;i<path.size();i++){
//构建一条路径,注意对末尾的-> 的处理
if(i!=path.size()-1){
strPath+=to_string(path[i])+"->";
}
else{
strPath+=to_string(path[i]);
}
}
// //把末尾的 - 和 > 删除掉,注意->是两个字符
// strPath.pop_back();
// strPath.pop_back();
res.push_back(strPath);
//找到一条路径后就结束了本次递归
return;
}
//递归逻辑:因为之前拿到的是叶子节点,所以递归的时候要跳过空节点
if(node->left!=NULL){
//每次递归后都要跟一个回溯,递归和回溯是一一对应的
getPath(node->left,path,res);
path.pop_back();
}
if(node->right!=NULL){
getPath(node->right,path,res);
//每次递归后都要跟一个回溯,递归和回溯是一一对应的
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
//记录结果字符串
vector<string> res;
//记录经过的节点值
vector<int> path;
getPath(root,path,res);
return res;
}
// //深度优先搜索
// vector<string> ans;
// void dfs(TreeNode* root, string path){
// if(!root) return ;
// path += to_string(root->val) + "->";
// if(!root->left && !root->right){
// path.pop_back();
// path.pop_back(); //去掉path中最后一个->
// ans.push_back(path);
// return ;
// }
// dfs(root->left, path);
// dfs(root->right, path);
// }
// vector<string> binaryTreePaths(TreeNode* root) {
// dfs(root, "");
// return ans;
// }
};No 404.左叶子之和(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/sum-of-left-leaves/
题目描述:
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0思路:这个题说实话第一眼看到感觉不像是简单题,可能是因为第一次接触到需要回溯的问题,而此前还没有接触过回溯。回溯问题一直有着会者不难,难者不会的说法。这个题目的总体思路是利用递归来记录经过的每一个节点的值,当遇到叶子节点的时候,说明这是一条完整的路径。将这个路径构造成字符串写入到结果集中。但是当走到了叶子结点后,怎么回退呢?这里就要用回溯的思想了。其实递归就是回溯的一种表现形式,递归本就是到底后再一层一层返回。如果我们在每次递归调用后再进行一次把路径节点值弹出的操作,那么当递归回退到这里的时候,就把这个已经使用过的节点的值弹出了,就可以实现回溯了。例如本题的代码中,我们对左节点进行递归,每当递归返回到这里时,说明当前这个节点后面所有的路径都已经找完了,当前这个节点的值就没有利用价值了,弹出后对右节点进行递归,也是一样的到道理。
递归的参数和返回值:返回值是当前左叶子节点的值 + 左子树的左叶子节点和 + 右子树的左叶子节点和。参数是节点。
递归终止条件:遇到左叶子节点,记录左叶子节点值,用于后续累加。
递归逻辑:递归左子树和右子树,寻找左叶子节点。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getLeftChildrenSum(TreeNode* node){
if(node==NULL){
return 0;
}
//递归寻找左子树和右子树的左叶子节点
int leftVal=getLeftChildrenSum(node->left);
int rightVal=getLeftChildrenSum(node->right);
//左叶子节点
int midVal=0;
//此时的node->left是左叶子节点,是要处理的节点
if(node->left!=NULL && node->left->left==NULL && node->left->right==NULL){
midVal=node->left->val;
}
return leftVal+rightVal+midVal;
}
int sumOfLeftLeaves(TreeNode* root) {
return getLeftChildrenSum(root);
}
};No 513. 找树左下角的值(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-bottom-left-tree-value/
题目描述:
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。
示例 1:
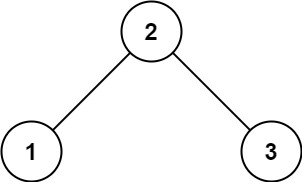
输入: root = [2,1,3]
输出: 1示例 2:
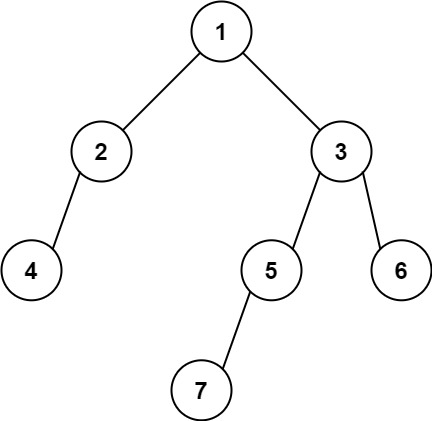
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7思路:这个题可以用层序遍历来迭代找到答案,也可以利用递归回溯找到答案。
层序遍历:层序遍历就比较简单了,我们只需要把层序遍历的每一层的第一个节点放入到结果集中,最后把结果集的最后一个结果返回即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//最左下角的值
int findBottomLeftValue(TreeNode* root) {
//层先遍历,res记录每一层最左边的值,res的最后一个就是最后一层最左边的值
queue<TreeNode*> treeQueue;
vector<int> res;
if (root != NULL) {
treeQueue.push(root);
}
while (!treeQueue.empty()) {
int levelSize = treeQueue.size();
vector<int> levelNum;
for (int i = 0; i < levelSize; i++) {
TreeNode* cur = treeQueue.front();
treeQueue.pop();
levelNum.push_back(cur->val);
if (cur->left != NULL) {
treeQueue.push(cur->left);
}
if (cur->right != NULL) {
treeQueue.push(cur->right);
}
}
//把每一层最左边节点的值添加到结果中
res.push_back(levelNum[0]);
}
//res保存的是每一层的最左边的节点值
return res.back();
}
};递归遍历:最底层的最左边的叶子节点。把这个条件拆分开,最底层的节点,那就是深度最大的节点。还要叶子节点,也好判断,孩子都为空就好。如何满足最左边的条件呢,这是关键。可以使用前序遍历,前序遍历先处理中间节点,可以知道这个节点是不是叶子节点,之后会优先处理左节点,这样找到的深度最大的叶子节点就在最左边。在递归的时候传入一个深度,每次往下递归就深度 + 1,递归返回后深度再 - 1,因为要进行回溯,当前遇到的最左边的叶子节点可能不是深度最大的。如果是叶子节点,那就看看当前的深度和传进来的最大深度谁大,然后把大的那个作为当前最深的节点,直到递归结束。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归,中序遍历优先搜索左边
int maxLeftDepth=INT_MIN;
int maxLeftVal;
void getMaxLeftDepth(TreeNode* node,int LeftDepth){
//记录叶子节点的深度,如果现在的深度是最大的,就记录
if(node->left==NULL&&node->right==NULL){
if(LeftDepth>maxLeftDepth){
maxLeftDepth=LeftDepth;
maxLeftVal=node->val;
}
return;
}
//递归左子树
if(node->left!=NULL){
//向下移动了一个节点
LeftDepth++;
getMaxLeftDepth(node->left,LeftDepth);
//回溯
LeftDepth--;
}
//递归右子树
if(node->right!=NULL){
LeftDepth++;
getMaxLeftDepth(node->right,LeftDepth);
LeftDepth--;
}
return ;
}
int findBottomLeftValue(TreeNode* root) {
getMaxLeftDepth(root,0);
return maxLeftVal;
}
};No 113. 路径总和 II(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum-ii/
题目描述:
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。
示例 1:
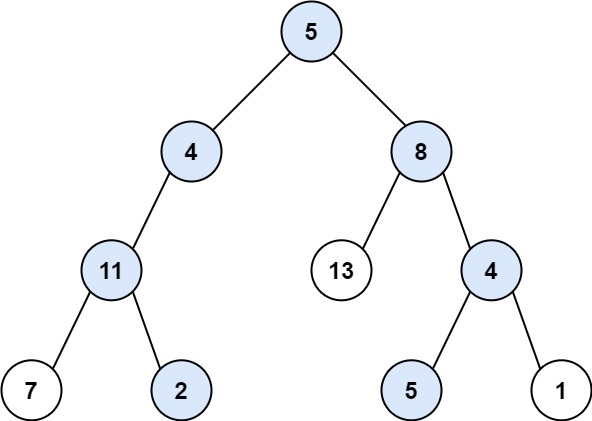
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]思路:这个题和之前做过的找出所有路径有很多相似之处,也是需要遍历所有的路径。总体思路就是深度优先搜索,递归前序遍历,统计从根节点出发到叶子节点的和,看是否等于targetSum。计算和不如计算差好,因为计算和的话每次递归到底都要累加一遍路径的节点值,如果在递归的时候每次把一个节点添加到路径中时,就 targetSum - node->val,并记为sumCount作为递归参数传递,那最后只需要看sumCount是不是0即可。
递归的参数和返回值:递归的参数就是节点,当前路径的节点值,targetSum - 当前路径的和是多少。因为要遍历所有的路径才能找到所有符合的路径,所以递归不需要返回值了。
递归的终止条件:当遇到叶子节点的时候,也就是左右孩子都为NULL的时候,就要看一下此时的target - 路径节点值的和 是多少了,如果是0,那这就是一条符合的路径,把当前的路径添加到结果集中。
递归的逻辑:从根节点出发,只要左节点不为空,就对左子节点递归调用。注意要回溯,因为肯能走到底以后发现这条路径行不通。因此在递归调用之前,要先把当前节点的左节点的值添加到路径集里面,然后计算当前的 sumCount,也就是sumCount - node->left->val,。然后再对左节点进行递归调用。递归终有返回的时候,在递归返回后,要对 sumCount 和 路径的节点 进行回溯,也就是递归调用之前做了什么,现在就做相反的事情。其实也可以直接把 sumCount 的表达式作为参数,这样就不用手动的在递归调用前做加减操作了,因为递归返回后sumCount还是当前的sumCount,我们没有对sumCount本身加减,但是这样回溯的标识就不明显了,不便与理解。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归
vector<vector<int>> res;
//递归函数
void getPath(TreeNode* node,vector<int>& pathVal,int sumCount){
//遇到叶子节点且此时sum等于target,就记录一下路径
if(node->left == NULL && node->right == NULL && sumCount == 0){
res.push_back(pathVal);
}
//递归左子树
if(node->left != NULL){
//可以把sumCount写成 sumCount - node->left->val 作为递归参数的形式,也可以回溯
pathVal.push_back(node->left->val);
sumCount -= node->left->val;
getPath(node->left, pathVal, sumCount);
//回溯
sumCount += node->left->val;
pathVal.pop_back();
}
//递归右子树
if(node->right != NULL){
pathVal.push_back(node->right->val);
sumCount -= node->right->val;
getPath(node->right, pathVal, sumCount);
//回溯
sumCount += node->right->val;
pathVal.pop_back();
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<int> pathVal;
if(root == NULL){
return res;
}
else{
pathVal.push_back(root->val);
}
getPath(root, pathVal, targetSum - root->val);
return res;
}
};还有一个题目和这个类似,是找到一条路径上的节点值的和等于 targetSum,找到了就返回true,否则返回false。其实做法和这个是一样的,只不过递归函数需要一个bool的返回值了,因为一旦找到就返回,并不需要继续再找了。只需要在最左右子树进行递归的时候加上条件判断,并在终止条件那里改一下,改为遇到了叶子节点并且SumCount == 0就返回true。
/*终止条件*/
//遇到叶子节点且当的sum为0
if(node->left == NULL && node->right == NULL && sumCount == 0){
return true;
}
//遇到叶子节点但是当前的sum不为0
if(node->left == NULL && node->right == NULL && sumCount != 0){
return false;
}
/*递归逻辑*/
//递归右子树,同上
if(node -> right != NULL){
if(getSum(node -> right , sumCount - node->right->val) == true){
return true;
}
}三、二叉的修改和改造
No 106. 从中序与后序遍历序列构造二叉树(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
题目描述:
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]思路:这个题目涉及到二叉树的构建相关知识。如果给一个前中后序中的一个遍历数组,是不能确定唯一的二叉树的。只有前序+中序或者中序+后序才能唯一确定一个二叉树。以中序 + 后序为例,说明如何构建一个二叉树。
首先要拿到后序数组的最后一个值,因为这个值一定是根节点。
然后找到这个值再中序数组中的位置,并以这个位置为界分为左半部分和右半部分的中序数组。
之后根据分割后的左半部分和右半部分中序数组,去分割之前的后序数组,把后序数组也分割为左半部分和右半部分,其中关键点是中序的左半部分长度和后序的左半部分长度相同。
最后递归切割,直到数组为空。其实这也是递归函数的递归逻辑。
递归的参数和返回值:递归的返回值是节点,因为要构造二叉树。递归的参数是中序数组和后序数组。用于构建二叉树。
递归的终止条件:当后数组的大小为0的时候,构建就完成了,递归开始返回。
递归的逻辑:1、判断数组的大小,为0则返回NULL
2、拿到后序数组的最后一个元素,并以这个值创建一个节点。
3、定位这个值在中序数组的位置
4、以这个位置对中序数组进行切割,切割的时候要注意区间的统一性且排除最大值。
5、通过切割后的中序数组切割后序数组,注意把用过的最后一个值删除。
6、对节点的左右孩子进行递归调用,注意切割后的左右前序后序数组。
注意点:切割的时候对区间的把握。要统一区间的开闭,这里统一使用左开右闭,即[a,b )。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//构造一颗二叉树需要两种遍历方式的数组,否则无法确定为唯一的二叉树
TreeNode* getTree(vector<int>& inorder, vector<int>& postorder) {
//1.如果数组的大小为零,说明是空节点,构造完成了
if(postorder.size() == 0){
return NULL;
}
//2.拿到后序数组的最后一个元素,这个元素就是当前的节点值
int rootVal = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootVal);
//只有一个节点
if(postorder.size() == 1){
return root;
}
//3.找到这个数字在中序数组中的位置,并把中序数组以此为界划分为两个数组
int index_postorderLastNum_In_inorder;
for(int i = 0; i < inorder.size(); i++){
if(inorder[i] == rootVal){
index_postorderLastNum_In_inorder = i;
break;
}
}
//4.切割中序数组,分为左右两个部分,以index_postorderLastNum_In_inorder为界,且跳过
vector<int> inorderAfterCutLeft(inorder.begin(), inorder.begin() + index_postorderLastNum_In_inorder);
vector<int> inorderAfterCutRight(inorder.begin() + index_postorderLastNum_In_inorder + 1, inorder.end());
//5.切割后序数组,分为左右两个部分
//首先把后序数组中之前用过的最后一个元素删除
postorder.pop_back();
//后序左边,后序数组的左边一定和前去数组的左边相同
vector<int> postorderAfterCutLeft(postorder.begin(), postorder.begin() + inorderAfterCutLeft.size());
//后序右边
vector<int> postorderAfterCutRight(postorder.begin() + inorderAfterCutLeft.size(), postorder.end());
//6.把切割后的数字继续递归,(前序切割后的左边,后序切割后的左边) && (前序切割后的右边,后序切割后的右边)
root->left = getTree(inorderAfterCutLeft, postorderAfterCutLeft);
root->right = getTree(inorderAfterCutRight, postorderAfterCutRight);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0 || postorder.size() == 0){
return NULL;
}
TreeNode* root = getTree(inorder, postorder);
return root;
}
};优化:原本的方法每次递归都会定义新的vector,空间消耗比较大,可以利用下标控制每次递归的左右数组得起始位置。注意如果使用下标作为参数,那寻找这个值在中序数组的位置的时候,i 遍历的区间就是传入的中序数组的起始和结束位置了,而不是0。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
/*优化:使用下标,不在递归中定义vector*/
//构造一颗二叉树需要两种遍历方式的数组,否则无法确定为唯一的二叉树
TreeNode* getTree(vector<int>& inorder, int inorder_start, int inorder_end, vector<int>& postorder, int postorder_start, int postorder_end) {
//1.如果数组的大小为零,说明是空节点,构造完成了
if(postorder_end == postorder_start){
return NULL;
}
//2.拿到后序数组的最后一个元素,这个元素就是当前的节点值
int rootVal = postorder[postorder_end -1];
TreeNode* root = new TreeNode(rootVal);
//只有一个节点
if(postorder_end - postorder_start == 1){
return root;
}
//3.找到这个数字在中序数组中的位置,并把中序数组以此为界划分为两个数组
int index_postorderLastNum_In_inorder;
for(int i = inorder_start; i < inorder_end; i++){
if(inorder[i] == rootVal){
index_postorderLastNum_In_inorder = i;
break;
}
}
//4.切割中序数组,分为左右两个部分,以index_postorderLastNum_In_inorder为界,且跳过
//[inorderAfterCutLeft_strat, inorderAfterCutLeft_end),所以区间长度就是 end - start
int inorderAfterCutLeft_strat = inorder_start;
int inorderAfterCutLeft_end = index_postorderLastNum_In_inorder;
//[inorderAfterCutRight_strat, inorderAfterCutRight_end),所以区间长度就是 end - start
int inorderAfterCutRight_strat = index_postorderLastNum_In_inorder + 1;
int inorderAfterCutRight_end = inorder_end;
//5.切割后序数组,分为左右两个部分
//后序左边一定和前序数组的左边相同,正常应该是起始位置 + 前序左边长度 -1, 但是由于左闭右开就不用-1
int postorderAfterCutLeft_start = postorder_start;
int postorderAfterCutLeft_end = postorder_start + (inorderAfterCutLeft_end - inorderAfterCutLeft_strat);
//后序右边
int postorderAfterCutRight_start = postorder_start + (inorderAfterCutLeft_end - inorderAfterCutLeft_strat);
int postorderAfterCutRight_end = postorder_end - 1;//最后一个元素不要
//6.把切割后的数字继续递归,(前序切割后的左边,后序切割后的左边) && (前序切割后的右边,后序切割后的右边)
root->left = getTree(inorder, inorderAfterCutLeft_strat, inorderAfterCutLeft_end, postorder, postorderAfterCutLeft_start, postorderAfterCutLeft_end);
root->right = getTree(inorder, inorderAfterCutRight_strat, inorderAfterCutRight_end, postorder, postorderAfterCutRight_start, postorderAfterCutRight_end);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0 || postorder.size() == 0){
return NULL;
}
TreeNode* root = getTree(inorder, 0, inorder.size(), postorder, 0, postorder.size());
return root;
}
};No 654. 最大二叉树(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-binary-tree/
题目描述:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:
输入:nums = [3,2,1]
输出:[3,null,2,null,1]思路:这个题目和前面构造二叉树的题目有相似之处,都是需要分割数组,只不过这个题目只需要分割一个,分割点就是最大的值的位置。并且这个最大值就是一个节点值。然后左边的数组继续相同的逻辑构造左子树,右边的数组继续相同的逻辑构造右子树。所以要用递归实现。
递归的参数和返回值:因为要构造二叉树,所以递归函数的返回值是节点。参数是一个用于构建二叉树的数组。
递归的终止条件:数组为空
递归的逻辑:如果数组为空,当前构造完成。拿到当前数组的最大值,并以这个最大值创建一个节点。用这个最大值分割当前的数组,并用分割后的左数组构建左子树,分割后的右数组构建右子树,也就是左孩子递归调用,参数是分割后的左数组,右孩子同理。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归函数,传递vector
TreeNode* buildTree(vector<int>& nums){
//1.数组为空
if(nums.size() == 0){
return NULL;
}
//2.拿到nums的最大值,并构建根节点,这个节点就是分割点
int maxVal = INT_MIN;
int indexOfMaxVal;
for(int i = 0;i < nums.size(); i++){
if(nums[i] > maxVal){
maxVal = nums[i];
indexOfMaxVal = i;
}
}
TreeNode* root = new TreeNode(maxVal);
if(nums.size() == 1){
return root;
}
//3.切割数组并递归调用
//不加判断的话就要在添加上终止条件
vector<int> leftNums(nums.begin(),nums.begin() + indexOfMaxVal);
root->left = buildTree(leftNums);
vector<int> rightNums(nums.begin() + indexOfMaxVal + 1, nums.end());
root->right = buildTree(rightNums);
// //添加了判断就不用加终止条件了
// if(indexOfMaxVal > 0){
// vector<int> leftNums(nums.begin(),nums.begin() + indexOfMaxVal);
// root->left = buildTree(leftNums);
// }
// if(indexOfMaxVal < nums.size() - 1){
// vector<int> rightNums(nums.begin() + indexOfMaxVal + 1, nums.end());
// root->right = buildTree(rightNums);
// }
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return buildTree(nums);
}
};优化:同上题一样,可以使用下标进行优化。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归函数,优化,使用下标
TreeNode* buildTree(vector<int>& nums, int nums_start, int nums_end){
//1.加上判断后,递归函数的数组不可能为空,否则需要添加终止条件
if(nums_end - nums_start <= 0){
return NULL;
}
//2.拿到nums的最大值,并构建根节点,这个节点就是分割点
int maxVal = INT_MIN;
int indexOfMaxVal;
for(int i = nums_start;i < nums_end; i++){
if(nums[i] > maxVal){
maxVal = nums[i];
indexOfMaxVal = i;
}
}
TreeNode* root = new TreeNode(maxVal);
//只有一个节点
if(nums_end - nums_start == 1){
return root;
}
//3.切割数组并递归调用,注意判断条件的时候要是用递归进来的参数
//不添加判断就就需要添加终止条件
// 左数组
int leftNums_start = nums_start;
int leftNums_end = indexOfMaxVal; //每次都会传入新的start和end,所以这end直接设置偏移量
root->left = buildTree(nums, leftNums_start, leftNums_end);
//右数组
int rightNums_start = indexOfMaxVal + 1;
int rightNums_end = nums_end;
root->right = buildTree(nums, rightNums_start,rightNums_end);
// //添加判断就不用添加终止条件了
// // 左数组
// if(indexOfMaxVal > nums_start){
// int leftNums_start = nums_start;
// //每次都会传入新的start和end,所以这end直接设置偏移量
// int leftNums_end = indexOfMaxVal;
// root->left = buildTree(nums, leftNums_start, leftNums_end);
// }
// //右数组
// if(indexOfMaxVal < nums_end - 1){
// int rightNums_start = indexOfMaxVal + 1;
// int rightNums_end = nums_end;
// root->right = buildTree(nums, rightNums_start,rightNums_end);
// }
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return buildTree(nums, 0, nums.size());
}
};No 617. 合并二叉树(简单)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-two-binary-trees/
题目描述:
给你两棵二叉树: root1 和 root2 。想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
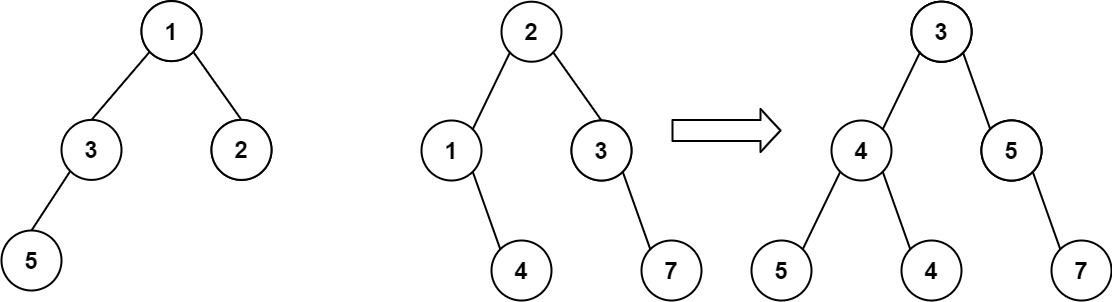
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]思路:这个题目最初想到的就是创建一颗新树,然后从树根开始同时遍历两颗给定的数,遇到的情况一共有三种:1、两个节点都不为空,那就把这两个节点的值相加作为新树的节点值;2、其中一个节点为空,那就把另一个节点的值作为新树的节点值;3、两个节点都为空,返回NULL;
还是使用递归来构建,这里使用那种遍历方式都可以。递归参数是两个节点,返回值是新的节点;递归的终止条件是两个节点都为空;递归的逻辑就是上面讲到的三种情况。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归构建二叉树,创建新树,空间消耗较大
TreeNode* buildTree(TreeNode* root1, TreeNode* root2) {
//如果两个节点都不为空,那新树的对应节点的值就是两个节点的和
if (root1 != NULL && root2 != NULL) {
TreeNode* root=new TreeNode(root1->val + root2->val);
//递归调用
root->left = buildTree(root1->left, root2->left);
root->right = buildTree(root1->right, root2->right);
}
//如果其中1个节点不为空,另一个为空,那新树的对应节点的值就是不为空的节点值
else if (root1 != NULL && root2 == NULL) {
TreeNode* root=new TreeNode(root1->val);
//递归的时候要把空节点的左右节点传入NULL,否则会空指针异常
root->left = buildTree(root1->left, NULL);
root->right = buildTree(root1->right, NULL);
}
//同上
else if (root1 == NULL && root2 != NULL) {
TreeNode* root=new TreeNode(root2->val);
//同上
root->left = buildTree(NULL, root2->left);
root->right = buildTree(NULL, root2->right);
}
else {
return NULL;
}
return root;
}
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
TreeNode* root = buildTree(root1, root2);
return root;
}
};优化:创建新树需要消耗空间,可以直接在其中一棵树上进行修改,同样使用递归。
递归的参数和返回值:参数是两个节点,在哪一颗树上进行修改那就返回哪一棵树的节点。
递归的终止条件:两个节点都为空。
递归的逻辑:。这里的递归逻辑大体上是一样的,只不过遇到其中一棵树的节点是空节点时,要返回另一颗数的节点。然后在处理其中一个节点为空的情况时,只需要处理当前修改的这颗树即可,以root1为例的话,只需要处理root1上的节点为空但是root2上节点不为空的情况。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//优化:递归构建二叉树,不创建新树,在其中一棵树上修改,如果一个节点为空,就返回另一个节点
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
//其中一个节点为空,那就返回另一个
if(root1 != NULL && root2 == NULL){
return root1;
}
else if(root1 == NULL && root2 != NULL){
return root2;
}
//都不为空就递归调用
else if(root1 != NULL && root2 != NULL){
root1->val = root1->val + root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
//都为空就返回NULL
else{
return NULL;
}
}
};迭代法:用层序遍历的迭代法也可以实现。用一个队列把两个树的节点保存起来,每次都先取出来,弹出。然后判断这两个节点的情况,都为空?都不为空?一个为空?根据不同的情况进行不同的操作即可。只有两个节点都不为空的时候才入队,否则只是选定其中一棵树,并一直在这棵树上修改即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//迭代法层序遍历也可以
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 == NULL) {
return root2;
}
if(root2 == NULL) {
return root1;
}
//使用队列
queue<TreeNode*> treeNodeQueue;
treeNodeQueue.push(root1);
treeNodeQueue.push(root2);
while(!treeNodeQueue.empty()) {
TreeNode* node1 = treeNodeQueue.front();
treeNodeQueue.pop();
TreeNode* node2 = treeNodeQueue.front();
treeNodeQueue.pop();
//此时两个节点一定不为空
node1->val = node1->val + node2->val;
if(node1->left != NULL && node2->left != NULL) {
treeNodeQueue.push(node1->left);
treeNodeQueue.push(node2->left);
}
if(node1->right != NULL && node2->right != NULL) {
treeNodeQueue.push(node1->right);
treeNodeQueue.push(node2->right);
}
//只需要处理root1为空且root2不为空的节点,因为是在root1上进行修改
if(node1->left == NULL && node2->left != NULL){
node1->left = node2->left;
}
if(node1->right == NULL && node2->right != NULL){
node1->right = node2->right;
}
}
return root1;
}
};四、二叉树的公共祖先
No 236. 二叉树的最近公共祖先(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
题目描述:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
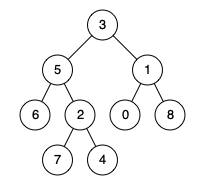
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1思路:这个题刚开始有点懵,首先想到了需要回溯,但是不知道在这个题中如何应用回溯。其实二叉树的后序遍历本身就是一个回溯的过程。先找到左右的节点,再往回反。既然涉及到回溯,那么回溯的好搭档递归也不可缺少了。
递归的参数和返回值:返回值是节点,因为需要利用递归得知是否存在两个目标节点,所以返回值理论上应该是bool,但是要求返回公共祖先节点,所以返回值应该是一个节点。参数就是节点和两个目标节点了。
递归终止条件:遇到空节或者遇到两个目标节点就返回当前的节点值。
递归逻辑:递归左子树和右子树,来确定左右子树中是否存在两个目标节点,并用两个节点进行记录,这两个用于记录的节点最终只有两种情况,要么是空,要什么给定的两个孩子节点。如果这两个节点都不为空,因为前面终止条件的缘故,此时的这两个用于记录节点一定是两个孩子节点,那此时递归传入的节点就是他们的最近公共祖先了;如果其中一个节点为空,那么说明两个孩子节点一定不在那一个分支上,一定在另一个分支上,而根据终止条件,此时不为空的那个节点一定是两个孩子节点中的一个,而且是靠上的那个,所以直接返回这个节点,这个就是公共祖先;如果两个都为空,说明当前递归传入的节点下不存在两个目标节点,返回NULL,递归返回后会去另一个分支寻找。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
//后序遍历,自带回溯
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//如果节点等于p或者q,那就返回,此时可能不是公共节点,如果不是公共祖先那么可以通过后面的逻辑修改
if(root == p || root == q || root == NULL){
return root;
}
//后序递归,左右中
TreeNode* leftTreeNode = lowestCommonAncestor(root->left, p, q);
TreeNode* rightTreeNode = lowestCommonAncestor(root->right, p, q);
//如果leftTreeNode和rightTreeNode不为空,说明在node节点下找到了p和q
if(leftTreeNode != NULL && rightTreeNode != NULL){
return root;
}
//如果leftTreeNode不为空,但是rightTreeNode为空,说明在node节点的右子树中没有q和p
else if(leftTreeNode != NULL && rightTreeNode == NULL){
//p和q都不在右子树,而且此时的leftTreeNode一定的等于p或者q,那么这一定是一个公共祖先,因为是先遍历到的
return leftTreeNode;
}
//如果leftTreeNode为空,但是rightTreeNode不为空,说说明在node节点的左子树中没有q和p
else if(leftTreeNode == NULL && rightTreeNode != NULL){
//p和q都不在左子树,而且此时的rightTreeNode一定的等于p或者q,那么这一定是一个公共祖先,因为是先遍历到的
return rightTreeNode;
}
//node节点下没有p和q
else{
return NULL;
}
}
};五、二叉搜索树的属性
No 98.验证二叉搜索树(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/validate-binary-search-tree/
题目描述:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true示例 2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。思路:这个题最简单的方法就是利用二叉搜索树中序遍历的有序性来做。整体思路就是使用中序递归遍历,得到一个遍历数组,这个数组必然是有序的,否则就不是一个二叉搜索树。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//中序递归遍历二叉树
void getNodeVal(TreeNode* root, vector<int>& val){
if(root == NULL){
return;
}
getNodeVal(root->left, val);
val.push_back(root->val);
getNodeVal(root->right,val);
}
//利用中序遍历构造一个数组,二叉搜索树的中序遍历得到的数组一定是有序的
bool isValidBST(TreeNode* root) {
vector<int> val;
getNodeVal(root, val);
//判断数组是否有序
for(int i=1; i < val.size(); i++){
//注意二叉搜索树的定义是左子树的值必须都小于根节点的值,等于也不行
if(val[i-1] >= val[i]){
return false;
}
}
return true;
}
};优化:在递归的同时就进行验证,不必最后在验证。其实在中序遍历的时候,只要下一个遍历到的节点值小于等于前一个遍历到的节点值,那就不符合二叉搜索树的定义了。关键是如何拿到前一个遍历到的节点。可以定义一个pre节点并初始化为NULL,后面开始递归,这个pre设置为当前这个节点就行,这样在下一次遍历开始前,先对pre进行一个判断,看看有没有pre,之后就可以拿当前接待和pre节点进行比较,确定是不是一个二叉搜索树了。用迭代法的中序遍历也可以,同样利用有一个pre保存前一个节点,在处理中间节点的逻辑上加上类似的处理即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* pre = NULL; // 用来记录前一个节点
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root; // 记录前一个节点
bool right = isValidBST(root->right);
return left && right;
}
};还要一个类似思路的题目,是找两个二叉搜索树中两个节点差值的绝对值的最小值。思路其实和这个题是一模一样的,可以先遍历拿到有序数组,再找最小差值。也可以利用pre节点,在递归或者迭代的过程中 ,计算当前节点和前一个节点的差值,并和记录的最小差值比较,更新小的差值即可。
No 501.二叉搜索树中的众数(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/
题目描述:
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
示例 1:
输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]思路:这个题一看涉及到了计数,判断某个节点出现的次数,首先就想到了要用哈希表来做。首先用一个中序递归遍历,得到二叉搜索树的节点值和出现次数的映射 map,然后因为不能对 map 的 value 进行排序,所以要把 map转化为另一种数据结构并根基 value进行排序。这里想到了两种。
1、把 map 转化为 大顶堆,类型是 pair<int, int> ,在构建大顶堆的同时传入自定义的排序方式,return child_1.second < child_2.second。得到大顶堆以后先用一个 val 保存一下堆顶的 second 值,然后在把大顶堆中所有 second = val 的 first 写入结果集中,这个first就是节点的值。注意题目中说众数不止一个。
2、把 map 转化为 vector,类型是pair<int, int>,然后导入 vector 中,导入完成后,利用sort 对 vector中数据的second按照降序进行排序,剩下的步骤和大顶堆就一样了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
/*普通二叉树的做法,遍历整棵树*/
//使用哈希表
unordered_map<int,int> count;
void getCount(TreeNode* node){
if(node == NULL){
return;
}
getCount(node->left);
count[node->val]++;
getCount(node->right);
}
//用于定义是小顶堆还是大顶堆,这里是大顶堆
class myCompareForPri{
public:
bool operator()(const pair<int,int>& child_1, const pair<int, int>& child_2){
return child_1.second < child_2.second;
}
};
//使用堆实现
vector<int> findMode(TreeNode* root) {
getCount(root);
//把unordered_map转换为大顶堆
priority_queue<pair<int, int>, vector<pair<int, int>>, myCompareForPri> pri_que;
for(unordered_map<int, int>::iterator it = count.begin(); it != count.end(); it++){
pri_que.push(*it);
}
//保存结果
vector<int> res;
//可能有多个节点的出现次数相同,所以先把堆顶的节点的出现次数记录下来
int maxCount = pri_que.top().second;
while(!pri_que.empty()){
//所有出现次数等于最大出现次数的的节点值都放入结果集
if(pri_que.top().second == maxCount){
res.push_back(pri_que.top().first);
}
pri_que.pop();
}
return res;
}
//给vec排序用
bool static myCompareForVec(const pair<int,int>& child_1, const pair<int, int>& child_2){
return child_1.second > child_2.second;
}
//使用vector实现
vector<int> findMode(TreeNode* root) {
getCount(root);
//把unordered_map转换为vector<pair<int, int>>
vector<pair<int, int>> mapToVec(count.begin(), count.end());
//对vector排序,按照value
sort(mapToVec.begin(), mapToVec.end(), myCompareForVec);
//保存结果
vector<int> res;
//可能有多个节点的出现次数相同,所以先把排好序的第一个节点的出现次数记录下来
int maxCount = mapToVec[0].second;
res.push_back(mapToVec[0].first);
for(int i = 1; i < mapToVec.size(); i++){
if(mapToVec[i].second == maxCount){
res.push_back(mapToVec[i].first);
}
else{
//遇到不同的说明后面就都不同了,已经排好序了
break;
}
}
return res;
}
};优化:利用二叉搜索树的有序性,还是使用中序递归。这里中序遍历中关键点在于中间节点的处理,其他部分和常规的中序递归遍历一样。这里要先定义几个全局的变量,用于记录出现的次数,最大的次数,之前的节点,最后的结果。
在处理中间节点时候,有这样几种情况:
1、pre是NULL,标明这是第一个节点,给count设置为1。
2、pre不是NULL且当前的节点值 == 之前的节点值,则count++。
3、如果pre不是NULL且当前节点值 不等于 之前的节点值,说明是一个新的节点,把count置为1从新计数。
这些都处理完以后,更新pre节点,设置为当前节点。要先判断count是否和countMax相等,相等的话就把当前节点的值也加入结果集中,因为可能有多个节点值出现次数相同。然后如果count 大于 countMax,那就压更新countMax,并且要把结果集清空,因为之前保存的节点值不是出现次数最大的了,然后再把当前节点值添加进去。
这里有一个陷阱,如果先执行更新最大值的逻辑,在执行把出现次数相同的节点值添加到结果集的逻辑,那么就会导致结果集更新不彻底,也就是说结果集已经清除了,现在又把出现次数等于之前最大出现次数的节点值放到了结果集中。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
/*优化:二叉搜索树的中序遍历本来就是有序的*/
int maxCount;
int count;
TreeNode* pre;
vector<int> res;
//递归遍历
void searchTree(TreeNode* node){
if(node == NULL){
return;
}
searchTree(node->left);
//中间节点,处理操作
//是第一个节点
if(pre == NULL){
count = 1;
}
//当前节点值等于前一个节点值
else if(node->val == pre->val){
count++;
}
//是一个新的节点值
else{
count = 1;
}
pre = node;
//还有另一个节点的出现次数也是maxCount
//要先判断是否还有出现相同次数的节点
//因为后面如果出现了次数更大的节点,先把之前出现次数最大的多个节点都放到结果集中,才能把所有不符合要求的节点都清除
if(count == maxCount){
res.push_back(node->val);
}
//找到了新的最大频率,要把结果集中之前保存的结果都清楚,重新记录
if(count > maxCount){
maxCount = count;
//清楚之前保存的结果,那些结果都不是出现次数最多的节点值了
res.clear();
res.push_back(node->val);
}
searchTree(node->right);
return;
}
vector<int> findMode(TreeNode* root) {
//初始化
count = 0;
maxCount = 0;
TreeNode* pre = NULL;
searchTree(root);
return res;
}
};六、二叉搜索树的改造
No 450.删除二叉搜索树中的节点(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/delete-node-in-a-bst/
题目描述:
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:首先找到需要删除的节点;如果找到了,删除它。
示例 1:
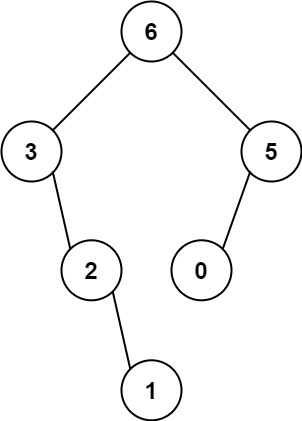
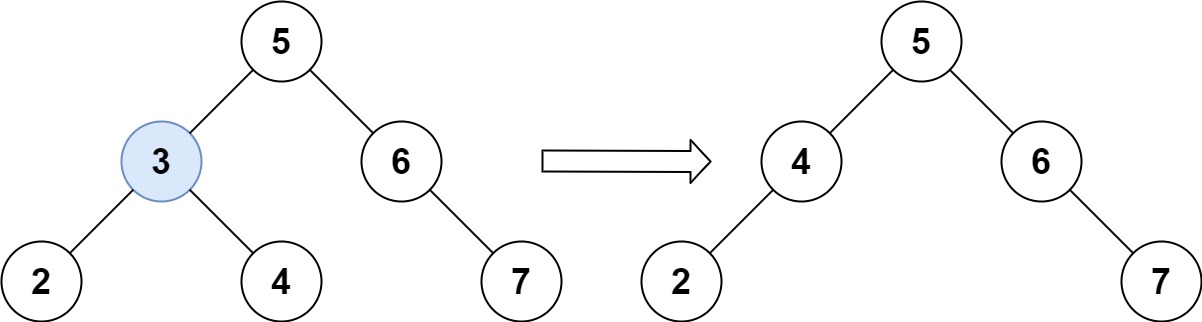
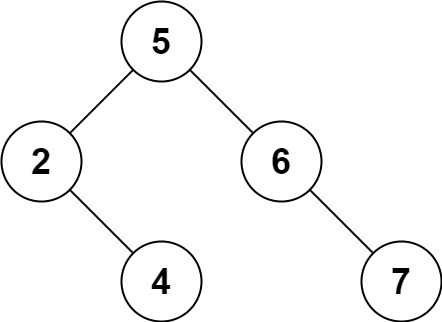
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []思路:这个题其实不难,只要根据要删除的节点的孩子节点的情况进行分类讨论即可。有这样几种情况:1、遍历完都没找到要删除的节点,直接返回root;2、找到了要删除的节点,要根据这个节点的孩子节点进行不同的操作:如果孩子节点为空,那就直接返回NULL;如果左孩子不为空且右孩子为空,那就返回左孩子的根节点;如果左孩子为空且右孩子不为空,那就返回右孩子根节点;如果左右孩子都不为空,那就要把整个左孩子的子树变为右孩子的最左下方节点的孩子,然后返回右节点。
其他几种情况都很好理解,只有最后这一个情况,需要仔细想一下。因为题目要求删除某个节点后,剩下的依然要构成二叉搜索树,所以要保证左子树所有节点值都小于右子树节点值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL){
//1、没找到要删除的节点
return root;
}
//找到了要删除的节点,但是有好多情况,注意分类
if(root->val == key){
//2、左右孩子都为空,直接删除,不用处理,返回NULL
if(root->left == NULL && root->right == NULL){
// delete root;
return NULL;
}
//3、左孩子为空,直接返回右孩子
else if(root->left == NULL){
TreeNode* node = root->right;
// delete root;
return node;
}
//4、右孩子为空,直接返回左孩子
else if (root->right == NULL){
TreeNode* node = root->left;
// delete root;
return node;
}
//5、左右孩子都不为空,最复杂,需要把要删除的节点的左孩子放到要删除的节点的右孩子的最左下方
//然后返回要删除的节点的右孩子节点
else{
TreeNode* cur = root->right;
while(cur->left != NULL){
cur = cur->left;
}
cur->left = root->left;
// TreeNode* temp = root;
root = root->right;
// delete temp;
return root;
}
}
else if(root->val > key){
root->left = deleteNode(root->left, key);
}
else if(root->val < key){
root->right = deleteNode(root->right, key);
}
return root;
}
};No 669. 修剪二叉搜索树(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/trim-a-binary-search-tree/
题目描述:
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
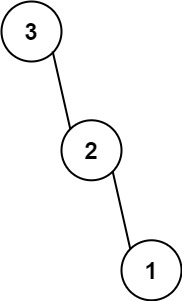
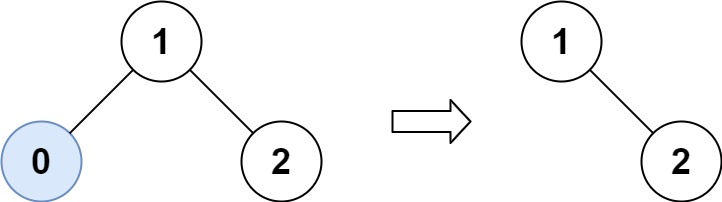
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]示例 2:
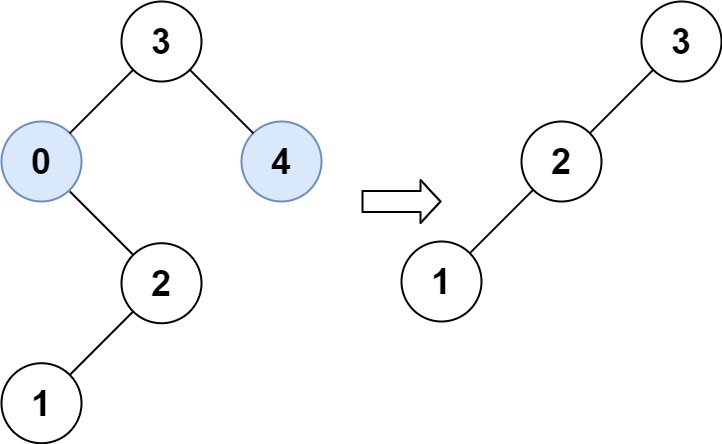
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]思路:这个题刚开始想复杂了,最开始的思路是,先中序遍历二叉搜索树,得到有序数组,再前序或者后序遍历二叉搜索树。然后根据题目给定的区间去修改中序遍历得到的有序数组,再根据修改后的中序数组去修改前序 / 后序数组,最后根据中序和 前序 / 后序数组构建二叉树。但是这样也太复杂了,涉及到很多时间复杂度较高的操作。其实这样想是因为还没有很好的理解递归和如何利用二叉搜索树的性质。
使用递归做更加简单,只要遍历到空节点,那就返回传进来的NULL。否则根据节点值和给定的区间的大小,来决定继续递归左子树还是右子树:如果节点值小于low,那就要找一个大一点的值,递归遍历右子树;如果节点值大于high,那就找一个小一点的值,递归左子树;否则说明这个节点在这个区间中,就继续递归左右子树。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root == NULL){
return root;
}
//节点值小于low,要找一个大的
if(root->val < low){
return trimBST(root->right, low, high);
}
//节点值大于high,要找一个小的
else if(root->val > high){
return trimBST(root->left, low, high);
}
//节点值在区间中,对左右孩子递归修剪
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};No 538.把二叉搜索树转换为累加树(中等)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/convert-bst-to-greater-tree/
题目描述:
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
示例 1:
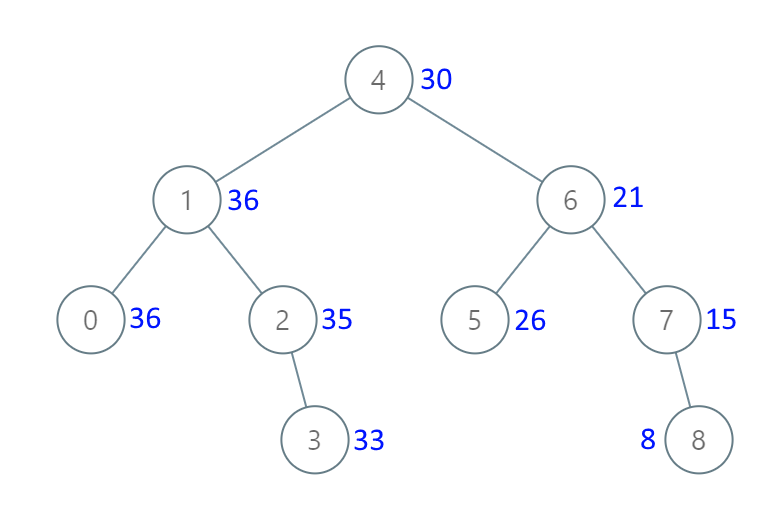
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]思路:这个题还是要利用二叉搜索树的特点,即中序遍历得到的是有序的数组。题目要求对这个树进行累加,根据题目给出的示例,根据要求构建的累加树也是一个二叉搜索树,只不过是反过来的二叉搜索树,变成了左子树节点值都大于根节点值,右子树节点值都小于根节点值。可以使用一个累加值 sum来记录累加和,然后使用 反着的中序遍历,也就是右中左,在遍历的时候,先把节点值累加到sum中,然后把这个节点值变为sum,之后继续递归即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//用于计算累加的和
int sum = 0;
// 中序遍历,因为返回的也要求是二叉搜索树,所以要从最右边往回走
TreeNode* getSum(TreeNode* node){
if(node == NULL){
return NULL;
}
//右节点
getSum(node->right);
//中间节点
sum += node->val;
node->val = sum;
//左节点
getSum(node->left);
return node;
}
TreeNode* convertBST(TreeNode* root) {
return getSum(root);
}
};