【README】
- 0. octave介绍:
- octave是什么: octave是一种开源编程语言,通过它可以快速实现机器学习算法,并提供丰富的画图功能;(专业的算法做专业的事情)
- 可以先使用 octave 构造算法原型(快速实现算法), 如果需要在大规模机器学习项目,再把算法通过c++或java来实现;
- octave优点:
- 在机器学习领域,人们通常选择的语言是 octave matlab python numPy 和 R;
- octave是开源免费的;matlab不是每个人都可以买得起;
- 相比于python, octave语法更加简单;
- 在机器学习领域,人们通常选择的语言是 octave matlab python numPy 和 R;
- 1. 本文总结自【吴恩达机器学习系列课程】,非常棒,墙裂推荐
- 2. octave安装,参见 Octave下载与安装教程_octave中editor如何下载-CSDN博客
【1】基本操作
【1.1】数学运算
octave:1> 56
ans = 56
octave:2> 5+6
ans = 11
octave:3> 1+2
ans = 3
octave:4> 1 == 2 % bool 运算
ans = 0
octave:5> 2^6 % 乘方
ans = 64
octave:6> 1 ~= 2 % 非
ans = 1
octave:7> 1 && 0 % 且
ans = 0
octave:8> 1 || 0 % 或
ans = 1补充: 修改前缀提示 octave 为 >>
octave:9> PS1('>> ');
>>
>> a = 3;
>> a【1.2】变量
>> a = 3; % 变量a,赋值为3 分号表示不打印
>> a % 打印变量a
a = 3
>> a=4
a = 4
>> a=pi;
>> a
a = 3.1416
>> disp(a) % disp 表示打印字符串
3.1416
>> disp(sprintf('2 decimals: %0.2f', a)) % 字符串格式化后打印
2 decimals: 3.14
>> format long % 格式化为long
>> a
a = 3.141592653589793
>> format short
>> a
a = 3.1416
>> b='hello world' % 声明字符串
b = hello world
>> b
b = hello world【1.3】矩阵操作
>> A = [1 2; 3 4; 5 6] % 定义矩阵
A =
1 2
3 4
5 6
>>
>> V = [ 1 2 3 ] % 定义行向量(矩阵)
V =
1 2 3
>> V=[1;2;3] % 定义列向量(矩阵)
V =
1
2
3
>> V=1:0.1:2 % 数组 最小值1 最大值2 步长0.1
V =
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
>> V=1:6 % 数组 最小值1 最大值6 步长1
V =
1 2 3 4 5 6
>>
>> ones(2,3) % 生成全为1的矩阵 ,2行3列
ans =
1 1 1
1 1 1
>> B = 2*ones(2,3) % 2乘以矩阵
B =
2 2 2
2 2 2【1.3.1】单位阵与直方图
>> D = zeros(1,3) % 0矩阵
D =
0 0 0
>> d = rand(3,3) % 随机数矩阵
d =
0.100062 0.491889 0.970450
0.397184 0.755019 0.036465
0.254940 0.213161 0.758412
>>
>> w = -6 + sqrt(10)*(randn(1,1000)); % randn产生高斯分布的数列
>> hist(w) %直方图
>> hist(w,50) % 直方图,50个柱子
>>
>> eye(4) % 单位阵
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> help eye % 帮助命令【2】移动数据(数据文件加载与保存)
【2.1】size与length函数
>> A = [1 2;3 4;5 6]
A =
1 2
3 4
5 6
>> size(A) % 获取矩阵大小,返回值是一个矩阵(1*2);3行2列
ans =
3 2
>> sz=size(A)
sz =
3 2
>> size(A,1) % 返回矩阵第1维度的大小
ans = 3
>> size(A,2) % 返回矩阵第2维度的大小
ans = 2
>>
>> V=[1 2 3 4] % 定义行向量
V =
1 2 3 4
>> length(V) % 行向量的最大维度 (length一般用于向量, 不用于矩阵)
ans = 4
>> length(A) % 矩阵的最大维度(2 3 取3)
ans = 3
>>【2.2】加载文件
>> pwd % 当前路径
ans = C:\Users\pacoson
>> cd D:\studynote\compute_basis\machine_learning\wuenda_ml\dataset %打开路径
>>
>> load featureX.dat % 加载文件
>> who % 查看变量
Variables visible from the current scope:
A B C D V a ans b d featureX featureY sz w
>> whos % 查看变量详情
Variables visible from the current scope:
variables in scope: top scope
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
B 2x3 48 double
C 1x3 24 double
D 1x3 24 double
V 1x4 32 double
a 1x1 8 double
ans 1x16 16 char
b 1x11 11 char
d 3x3 72 double
featureX 9x2 144 double
featureY 9x1 72 double
sz 1x2 16 double
w 1x1000 8000 double
Total is 1088 elements using 8515 bytes
>> clear b % 清空变量b
>>【2.3】保存数据到文件
>> load priceY.dat % 加载文件
>>
>> whos
Variables visible from the current scope:
variables in scope: top scope
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
B 2x3 48 double
C 1x3 24 double
D 1x3 24 double
V 1x4 32 double
a 1x1 8 double
ans 1x16 16 char
d 3x3 72 double
featureX 9x2 144 double
priceY 9x1 72 double
sz 1x2 16 double
w 1x1000 8000 double
Total is 1077 elements using 8504 bytes
>> v=priceY(1:5) % priceY矩阵的前5行赋值给v
v =
11234
86234
21334
44244
51235
>> whos
Variables visible from the current scope:
variables in scope: top scope
Attr Name Size Bytes Class
==== ==== ==== ===== =====
A 3x2 48 double
B 2x3 48 double
C 1x3 24 double
D 1x3 24 double
V 1x4 32 double
a 1x1 8 double
ans 1x16 16 char
d 3x3 72 double
featureX 9x2 144 double
priceY 9x1 72 double
sz 1x2 16 double
v 5x1 40 double
w 1x1000 8000 double
Total is 1082 elements using 8544 bytes
>> save copyOfPriceY.mat v; % 保存为.mat文件,会压缩数据,用于保存大数据
>>
>> clear
>> load copyOfPriceY.mat
>> whos
Variables visible from the current scope:
variables in scope: top scope
Attr Name Size Bytes Class
==== ==== ==== ===== =====
v 5x1 40 double
Total is 5 elements using 40 bytes
>>
>> save copyOfPriceY3.txt v -ascii; % 保存变量v到txt文本文件 编码为ascii
>>【2.4】矩阵操作
>> A=[1 2;3 4;5 6] % 定义矩阵
A =
1 2
3 4
5 6
>> A(3,2) % 获取矩阵A的值,坐标第3行第2列
ans = 6
>> A(2,:) % 获取矩阵A的第2行 (行向量)
ans =
3 4
>> A(:,2) %获取矩阵A的第2列的列向量
ans =
2
4
6
>> A([1 3],:) % 获取矩阵第1行和第3行的行向量
ans =
1 2
5 6
>> A
A =
1 2
3 4
5 6
>> A(:,2) % 矩阵第2列的列向量
ans =
2
4
6
>> A(:,2)=[10;11;12] % 赋值: 给矩阵A第2列的列向量赋值,赋值后形成新的矩阵A
A =
1 10
3 11
5 12
>> A=[A,[100;101;102]] % 给矩阵A新增一个列向量
A =
1 10 100
3 11 101
5 12 102
>> A(:) % 收集并打印A的所有元素
ans =
1
3
5
10
11
12
100
101
102
>> A=[1 2;3 4;5 6];
>> B=[11 12;13 14;15 16]
B =
11 12
13 14
15 16
>> C=[A B] % 把B作为新列向量拼接
C =
1 2 11 12
3 4 13 14
5 6 15 16
>> C=[A;B] % 把B作为新行向量拼接
C =
1 2
3 4
5 6
11 12
13 14
15 16【3】矩阵计算
【3.1】矩阵运算
>> A=[ 1 2;3 4;5 6]
A =
1 2
3 4
5 6
>> B=[11 12;13 14;15 16]
B =
11 12
13 14
15 16
>> C=[1 1 ;2 2]
C =
1 1
2 2
>> A*C % 矩阵乘法
ans =
5 5
11 11
17 17
>> A.*B % 对应位置的元素相乘
ans =
11 24
39 56
75 96
>> A.^2 % 矩阵每个元素平方
ans =
1 4
9 16
25 36【3.2】矩阵函数
>> V=[1;2;3]
V =
1
2
3
>> 1./V % 矩阵元素的倒数
ans =
1.0000
0.5000
0.3333
>> 1./A
ans =
1.0000 0.5000
0.3333 0.2500
0.2000 0.1667
>> log(V) # 每个元素求对数
ans =
0
0.6931
1.0986
>> abs(V) % 绝对值
ans =
1
2
3【3.3】矩阵转置
>> V+1 % 矩阵加法
ans =
2
3
4
>> A
A =
1 2
3 4
5 6
>> A' % 转置
ans =
1 3 5
2 4 6【3.4】矩阵元素的函数
>> A=[1 15 2 0.5]
A =
1.0000 15.0000 2.0000 0.5000
>> val=max(A) % 找出矩阵元素的最大值
val = 15
>> [val,ind]=max(A) % 找出矩阵元素的最大值和下标
val = 15
ind = 2
>> A < 3
ans =
1 0 1 1
>>
>> find(A<3) % 找出小于3的元素的下标
ans =
1 3 4
>> A
A =
1.0000 15.0000 2.0000 0.5000
>> sum(A) % 矩阵元素累加
ans = 18.500
>> prod(A) % 矩阵元素相乘
ans = 15
>> floor(A) % 矩阵元素向下取整数
ans =
1 15 2 0
>> ceil(A) % 向上取取整
ans =
1 15 2 1
>> rand(3) % 随机值矩阵
ans =
0.4904 0.4963 0.9169
0.7345 0.5650 0.5107
0.7243 0.4943 0.4580
>> max(rand(3), rand(3)) % 随机值矩阵最大元素构成的矩阵
ans =
0.8598 0.9433 0.5683
0.4264 0.4045 0.3570
0.6971 0.1840 0.7685
>>
【3.5】魔法矩阵及其运算
>> M=magic(3) % 魔法矩阵magic,每行元素或每列元素或对角线上元素累加值相同
M =
8 1 6
3 5 7
4 9 2
>> [r,c]=find(M>=7) % 找出大于等于7的元素的位置 第1行第1列,第3行第2列,第2行第3列;
r =
1
3
2
c =
1
2
3
>> M
M =
8 1 6
3 5 7
4 9 2
>> max(M, [], 1) % 计算每列的最大元素
ans =
8 9 7
>> max(M, [], 2) % 计算每行的最大元素
ans =
8
7
9
>> max(M) % 默认% 计算每列的最大元素
ans =
8 9 7
>> max(max(M)) % 整个矩阵的最大元素
ans = 9
>>
>> M(:) % 把矩阵所有列向量转为一个列向量
ans =
8
3
4
1
5
9
6
7
2
>> max(M(:))
ans = 9【3.5.1】计算魔法矩阵的元素累加和
>> M=magic(9)
M =
47 58 69 80 1 12 23 34 45
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35
>> sum(M,1) % 求每个列向量的元素累加和
ans =
369 369 369 369 369 369 369 369 369
>> sum(M,2) % 求每个行向量的元素累加和
ans =
369
369
369
369
369
369
369
369
369
>> M.*eye(9) % 矩阵点乘单位阵
ans =
47 0 0 0 0 0 0 0 0
0 68 0 0 0 0 0 0 0
0 0 8 0 0 0 0 0 0
0 0 0 20 0 0 0 0 0
0 0 0 0 41 0 0 0 0
0 0 0 0 0 62 0 0 0
0 0 0 0 0 0 74 0 0
0 0 0 0 0 0 0 14 0
0 0 0 0 0 0 0 0 35
>> M.*flipud(eye(9)) % 矩阵点乘反向单位阵
ans =
0 0 0 0 0 0 0 0 45
0 0 0 0 0 0 0 44 0
0 0 0 0 0 0 43 0 0
0 0 0 0 0 42 0 0 0
0 0 0 0 41 0 0 0 0
0 0 0 40 0 0 0 0 0
0 0 39 0 0 0 0 0 0
0 38 0 0 0 0 0 0 0
37 0 0 0 0 0 0 0 0
>>
>> M=magic(3)
M =
8 1 6
3 5 7
4 9 2
>> pinv(M) % 求伪逆
ans =
0.147222 -0.144444 0.063889
-0.061111 0.022222 0.105556
-0.019444 0.188889 -0.102778
>> M*pinv(M) % 矩阵乘以矩阵的逆得到单位阵
ans =
1.0000e+00 -1.1380e-14 6.3005e-15
1.7347e-17 1.0000e+00 -1.3878e-17
-5.8148e-15 1.2768e-14 1.0000e+00【4】数据绘制(画图)(可视化)
1. 通过绘制模型结果的图像,可以促使研究人员更好的优化算法;
2. 画图函数 plot();
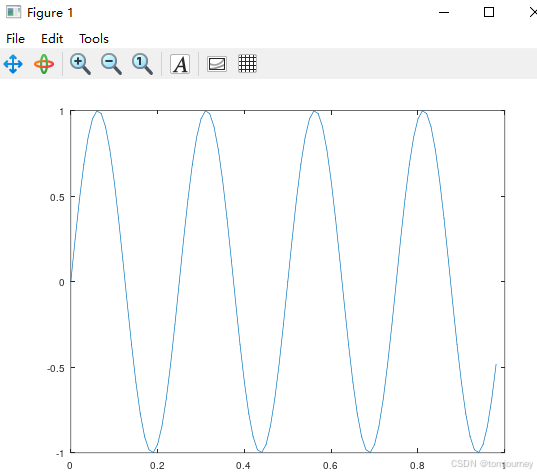
【4.1】正弦与余弦函数
>> t=[0:0.01:0.98];
>> y1=sin(2*pi*4*t); % 正弦函数
>> plot(t,y1);
>>
>> y2=cos(2*pi*4*t); % 余弦函数
>> plot(t,y2);
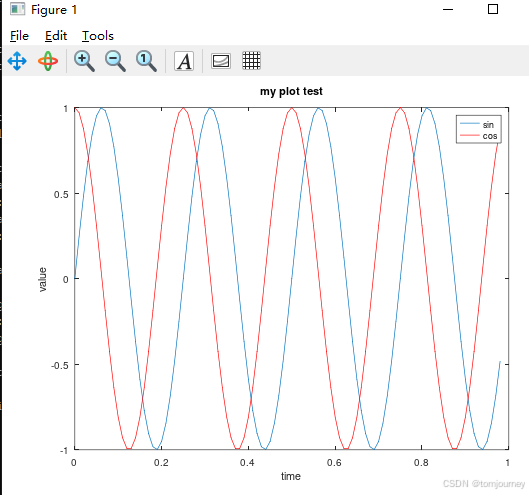
>>【4.2】多个函数在一个画布上画图
>> plot(t, y1); % 画 sin 图
>> hold on; % 等待,在同一个画图上画第2个函数
>>
>> plot(t, y2,'r'); % 画第2个函数 cos ,且 r=红色
>> xlabel('time');ylabel('value'); % 设置x标签,y标签名称
>> legend('sin', 'cos'); % 添加线条说明
>>
>> title('my plot test') % 新增图标题
>>
>> print -dpng 'myplot.png' % 保存到本地
>> close % 关闭画步
【4.3】为图像标号(如 1 2 3 )
>> figure(1);plot(t, y1); // 声明画布1
>> figure(2);plot(t, y2,'r'); // 画布2
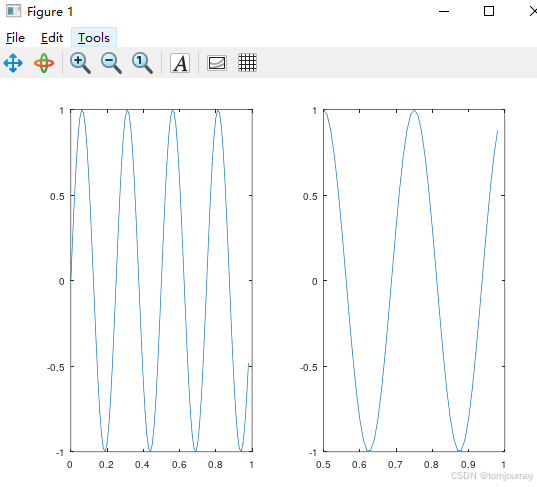
>>【4.4】把画布分割为多个格子
(即一个画布用于展示多个模型的图像)
>> subplot(1,2,1); %把画布分为 1*2的格子,使用第1个格子
>> plot(t, y1); % 把图像画在第1个格子
>> subplot(1,2,2); %把画布分为 1*2的格子,使用第2个格子
>> plot(t,y2); % 把图像画在第2个格子
>>
>> axis([0.5 1 -1 1]) % 修改第2个格子图像的坐标 (横坐标范围0.5到1,纵坐标范围 -1 到1)补充:清除图像: clf;
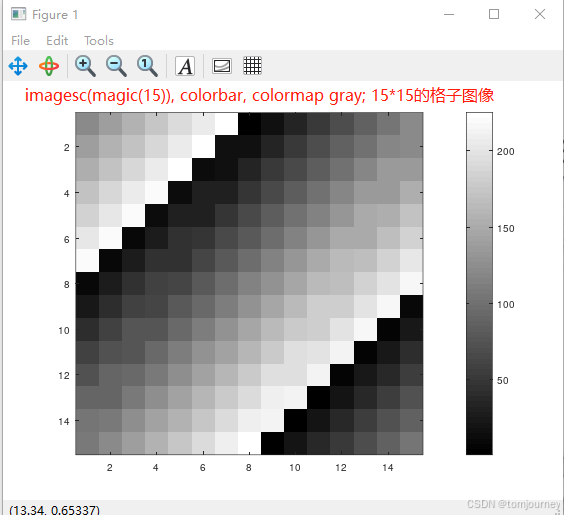
【4.5】彩色图与颜色条
>> M = magic(5);
>> imagesc(M) % 彩色格子图
>>
>> imagesc(M), colorbar, colormap gray; % 逗号分割,同时执行3条命令;colorbar带颜色条
>> M
M =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
【5】控制语句for-whole-if
【5.1】for循环与while循环
>> v=zeros(10,1) %定义10*1的矩阵,值为0
v =
0
0
0
0
0
0
0
0
0
0
>> for i=1:10, % 声明for循环
> v(i)=2^i;
> end; % 结束标志
>> v
v =
2
4
8
16
32
64
128
256
512
1024
>> i=1;
>> while i<=5, % 声明while循环
> v(i)=100;
> i=i+1;
> end; % while循环结束
>> v
v =
100
100
100
100
100
64
128
256
512
1024【5.2】if判断语句
>> i=1;
>> while true,
> v(i)=999;
> i=i+1;
> if i == 6, % if判断语句
> break;
> end ; % if结束
> end ;
>> v
v =
999
999
999
999
999
64
128
256
512
1024
>>
>> v(1)=2;
>> if v(1)==1, disp('one'); % if判断
> elseif v(1) == 2, disp('two') % elseif判断
> ;else disp('other'); % else判断
> end; % if判断结束
two
>>【5.3】定义函数
函数声明: 新建 mysqure.m 文件,如下:
function y = mysqure(x)
y=x^2;>> mysqure(3) % 搜索路径下查找函数 mysuqre ,并执行
ans = 9
>> addpath('D:\studynote\compute_basis\machine_learning\wuenda_ml\dataset') % 把路径添加到函数搜索路径
>>
>> mysqure(5)
ans = 25【5.3.1】定义返回多个值的函数
function [y1,y2] = mysqureReturnResults(x)
y1=x^2;
y2=x^3;执行函数结果:
>> [r1, r2] = mysqureReturnResults(5)
r1 = 25
r2 = 125
>>【5.3.2】例子-计算成本函数值
function J = costFunJ(X, y, theta)
m = size(X,1) % 训练集个数
predictions = X * theta; % 预测值
sqrErrors = (predictions-y).^2; % 误差
J= 1/(2*m) * sum(sqrErrors); % 成本函数>> X=[1 1;1 2;1 3] % 定义X矩阵
X =
1 1
1 2
1 3
>> y=[1; 2; 3] % 定义预测值向量y
y =
1
2
3
>> theta=[0;1]; % 定义模型参数 theta
>> j=costFunJ(X,y,theta) % 送入成本函数,计算成本
m = 3
j = 0
>> theta=[0;0]; % 更换模型参数,再次计算成本
>>
>> j=costFunJ(X,y,theta)
m = 3
j = 2.3333 【6】矢量 (向量化)
使用各种语言提供的数值线性函数库,计算会更加高效;
此外,代码也会更少, 出错少,而且运行高效(因为底层做了并行优化,更好利用硬件资源);